В системах передачи сообщений обычно используется ансамбль сигналов
![]() (2.128)
(2.128)
При двоичной передаче этот ансамбль состоит всего из двух сигналов. В многопозиционной системе число сигналов равно основанию кода т, в многоканальной системе — числу каналов. Передаваемые сигналы, очевидно, должны отличаться друг от друга настолько, чтобы их можно было уверенно различить, а следовательно, разделить на приеме.
Геометрически каждому сигналу (2.128) соответствует вектор в n-мерным пространстве. Мы полагаем здесь, что сигналы имеют одинаковую длительность Т и ограничены полосой частот F. Квадрат расстояния между любой парой сигналов (векторов) согласно (2.124) равен:
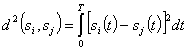 (2.129)
(2.129)
Величина расстояния d полностью характеризует различие между сигналами: чем больше d, тем больше это различие. Раскрывая скобки в (2,129), получаем
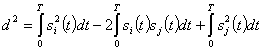
Крайние члены определяют энергию сигналов, а средний член — взаимную корреляцию между сигналами. Для сигналов, имеющих одинаковую энергию
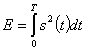
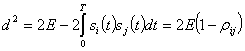 (2.130)
(2.130)
где 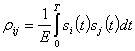 (2.131)
(2.131)
— коэффициент взаимной корреляции сигналов.
Итак, различие между сигналами полностью определяется коэффициентом взаимной корреляции ![]() между ними. С увеличением
между ними. С увеличением ![]() различие между сигналами уменьшается и их полное разделение на приеме становится невозможным.
различие между сигналами уменьшается и их полное разделение на приеме становится невозможным.
Условием разделения сигналов является выполнение неравенства
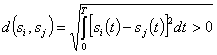 (2.132)
(2.132)
откуда
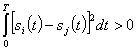
или
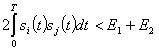 (2.133)
(2.133)
В случае сигналов с равными энергиями ![]()
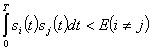 (2.134)
(2.134)
или
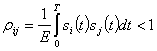 (2.135)
(2.135)
Таким образом, для того чтобы можно было разделить сигналы равных энергий, их скалярное произведение (для случайных сигналов — функция взаимной корреляции) должно быть меньше энергии любого из них или коэффициент корреляции при ![]() меньше единицы.
меньше единицы.
Из выражения (2.135) непосредственно следует, что ортогональность сигналов является достаточным условием их разделения. В случае
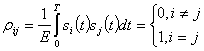
Таким образом, степень различия между сигналами можно характеризовать величиной коэффициента ![]() или коэффициента различимости
или коэффициента различимости
![]() (2.137)
(2.137)
В системах двух сигналов максимальная различимость будет иметь место при выполнении условия
![]() (2.138)
(2.138)
Сигналы, удовлетворяющие равенству (2.138), называются противоположными. С геометрической точки зрения противоположные сигналы представляются векторами, сдвинутыми друг относительно друга на угол π. Для противоположных сигналов ![]() , для ортогональных
, для ортогональных ![]() , для всех других сигналов
, для всех других сигналов ![]() .
.
Заметим, что задача разделения сигналов в той или иной форме возникает всегда при передаче сообщений по каналам связи. Эта задача возникает не только при разделении полезных сигналов, но и при выделении полезных сигналов из помех.

