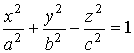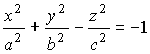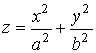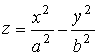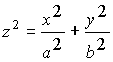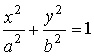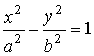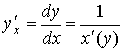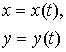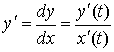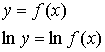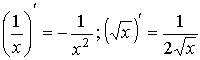3.3. Поверхности второго порядка
4.1. Алгебраическая форма комплексного числа
4.2. Действия над комплексными числами в алгебраической форме
4.3. Тригонометрическая форма комплексного числа
4.4. Показательная форма комплексного числа
4.5. Действия над комплексными числами в тригонометрической и показательной форме
6. Дифференциальное исчисление
6.2. Основные правила дифференцирования
6.3. Производные основных элементарных функций
1. Линейная алгебра
1.1. Определители (детерминанты)
Обозначения определителя матрицы А: D , det A,![]() .
.
Определитель второго порядка: 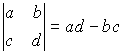 .
.
Определитель третьего порядка:
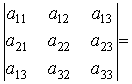
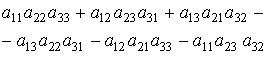
Разложение определителя n-го порядка по i-й строке: 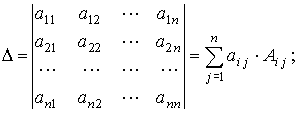
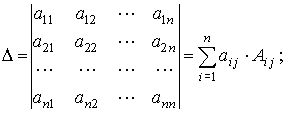
Разложение определителя n-го порядка по j-ому столбцу:
![]() -алгебраическое дополнение элемента
-алгебраическое дополнение элемента ![]() ,
, ![]() ,
,
![]() -минор элемента
-минор элемента ![]() , т.е. определитель, получаемый из исходного определителя вычёркиванием i-й строки и j-го столбца.
, т.е. определитель, получаемый из исходного определителя вычёркиванием i-й строки и j-го столбца.
1.2. Матрицы
| Матрица размерами n x m (n строк и m столбцов): | 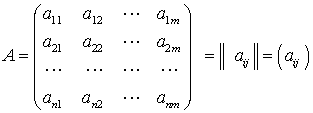 , ,
где |
Равенство матриц: ![]() , если эти матрицы одного размера и
, если эти матрицы одного размера и ![]() .
.
Квадратная матрица порядка n: ![]() .
.
Сложение матриц: ![]() , где
, где ![]() .
.
Свойства сложения матриц:
1) ассоциативность: ![]() ;
;
2) коммутативность: ![]() ;
;
Умножение матрицы на число: ![]() .
.
Умножение матриц: 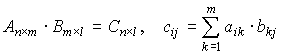 .
.
Свойства умножения матриц:
-
- ассоциативность:
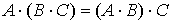 ;
; - некоммутативность.
- определитель произведения квадратных матриц:
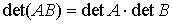 .
.
- ассоциативность:
Транспонирование матрицы: ![]() .
.
Свойство транспонирования произведения матриц: ![]() .
.
Невырожденная (неособая) матрица: ![]() .
.
Обратная матрица для невырожденной матрицы A: ![]() .
.
Свойства обратной матрицы:
1) ![]() ;
;
2) ![]() .
.
Виды матриц:
единичная матрица: 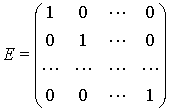
симметрическая матрица: ![]()
![]()
ортогональная матрица: A - невырождена и ![]()
кососимметрическая матрица: ![]() ;
;
матрица-строка: ![]()
матрица-столбец: ![]() .
.
Ранг матрицы ![]() - наибольший порядок её ненулевого минора или наибольшее число линейно независимых строк (столбцов) матрицы.
- наибольший порядок её ненулевого минора или наибольшее число линейно независимых строк (столбцов) матрицы.
1.3. Системы линейных уравнений
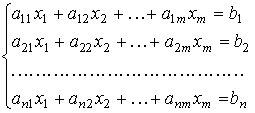 |
|
Матричный вид: ![]() ,
, ![]() - матрица системы,
- матрица системы,
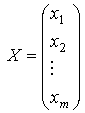 |
- столбец неизвестных, |
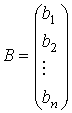 |
- столбец свободных членов. |
Совместность системы: ![]() , где
, где ![]() - расширенная матрица системы (теорема Кронекера-Капелли).
- расширенная матрица системы (теорема Кронекера-Капелли).
Формулы Крамера (n=m): ![]() ,
, ![]() - определитель матрицы системы;
- определитель матрицы системы; ![]() -определитель, полученный при замене i-го столбца матрица A на столбец В.
-определитель, полученный при замене i-го столбца матрица A на столбец В.
Однородная система (B=0):
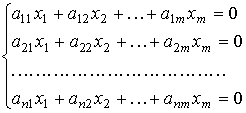 |
Если то система им то существуют ненулевые решения. |
2. Векторная алгебра
|
Наименование |
Обозначение, формула |
|
Вектор и его выражение в декартовых координатах |
a=ax i+ay j+az k=(ax, ay, az) |
|
Модуль (длина) вектора |
|
|
Направляющие косинусы вектора |
|
|
Сложение двух векторов |
a+b=(ax+bx, |
|
Умножение вектора на скаляр |
ka=(kax, |
|
Скалярное произведение двух векторов |
|
| Скалярное произведение в декартовых координатах |
ab=axbx+ayby+azbz |
|
Условие ортогональности двух ненулевых векторов |
ab=0 |
|
Векторное произведение двух векторов |
|
|
Векторное произведение в декартовых координатах |
|
|
Условие коллинеарности двух ненулевых векторов |
|
|
Смешанное произведение трех векторов |
|
|
Смешанное произведение в декартовых координатах |
|
|
Условие компланарности трех ненулевых векторов |
abc=0 векторы (лежат в одной плоскости) |
| Линейно независимая система векторов | {a1,a2,…,an} - линейно независима 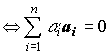 только при условии только при условии |
3. Аналитическая геометрия
3.1. Линейные образы
3.1.1. Прямая на плоскости
Виды уравнений
|
Уравнение |
Наименование |
Параметры |
| общее уравнение прямой на плоскости | n=(A,B) - нормальный вектор прямой;
k - a - отрезок, отсекаемый прямой на оси х; b - отрезок, отсекаемый прямой на оси y; q=(l,m) - направляющий вектор прямой |
|
| уравнение прямой, проходящей через данную точку | ||
| уравнение прямой с данным угловым коэффициентом | ||
| уравнение прямой, проходящей через данную точку с данным угловым коэффициентом | ||
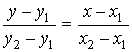 |
уравнение прямой, проходящей через две точки | |
| уравнение прямой в отрезках | ||
| каноническое уравнение прямой |
Формулы для вычисления угла между двумя прямыми на плоскости:
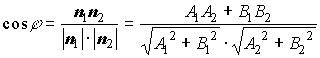 ;
; 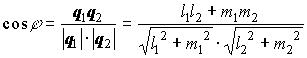 ,
,
где ![]() и
и ![]() -нормальный и направляющий векторы первой прямой;
-нормальный и направляющий векторы первой прямой;
![]() и
и ![]() - нормальный и направляющий векторы второй прямой.
- нормальный и направляющий векторы второй прямой.
Условия параллельности двух прямых на плоскости:
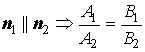 ;
;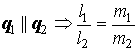 ;
;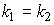 , где
, где 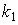 и
и 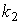 - угловые коэффициенты прямых.
- угловые коэффициенты прямых.
Условия перпендикулярности двух прямых на плоскости:
- n1
 n2
n2  n1
n1 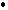 n2=0 или A1A2+B1B2=0;
n2=0 или A1A2+B1B2=0; - q1
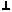 q2
q2 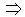 q1
q1 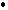 q2=0 или l1l2+m1m2=0;
q2=0 или l1l2+m1m2=0; 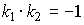
3.1.2. Плоскость в пространстве
Виды уравнений
|
Уравнение |
Наименование |
Параметры |
| общее уравнение плоскости в пространстве |
a,b,c – отрезки, отсекаемые плоскостью
p - длина перпендикуляра, опущенного |
|
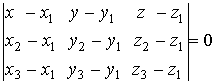 |
уравнение плоскости, проходящей через три точки |
|
| уравнение плоскости в отрезках | ||
|
нормальное уравнение плоскости |
Выражение направляющих косинусов через координаты нормального вектора:
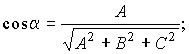
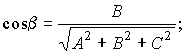
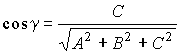 .
.
Формулы для вычисления угла между двумя плоскостями:
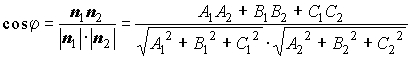 ;
;
где![]() и
и ![]() -нормальные векторы плоскостей.
-нормальные векторы плоскостей.
Условие параллельности двух плоскостей:
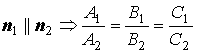 .
.
Условие перпендикулярности двух плоскостей:
n1![]() n2
n2 ![]() n1
n1![]() n2=0 или A1A2+B1B2+С1С2=0.
n2=0 или A1A2+B1B2+С1С2=0.
3.1.3. Прямая в пространстве
Виды уравнений
|
Уравнение |
Наименование |
Параметры |
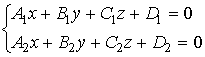 |
общие уравнения прямой в пространстве | направляющий вектор прямой; координаты фиксированных точек на прямой |
| канонические уравнения прямой в пространстве | ||
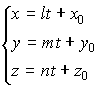 |
параметрические уравнения прямой в пространстве | |
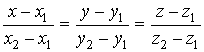 |
уравнения прямой, проходящей через две фиксированные точки |
Формулы для вычисления угла между двумя прямыми в пространстве:
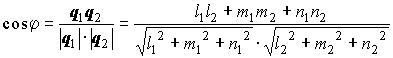 ,
,
где ![]() и
и ![]() - направляющие векторы прямых.
- направляющие векторы прямых.
Условие параллельности двух прямых в пространстве:
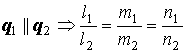 .
.
Условие ортогональности двух прямых в пространстве:
q1 ![]() q2
q2 ![]() q1
q1 ![]() q2=0 или l1l2+m1m2+n1n2=0.
q2=0 или l1l2+m1m2+n1n2=0.
3.2. Кривые второго порядка
Общее уравнение кривой второго порядка:
![]() .
.
3.2.1. Окружность
| Каноническое уравнение:
Радиус окружности: a. |
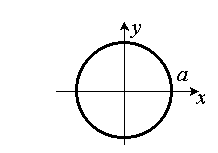 |
||||
| Параметрическое уравнение: | 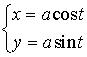 |
Уравнение в полярных координатах: | |||
| Уравнение окружности радиуса |
|||||
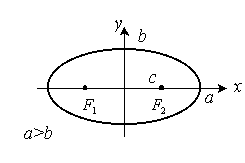
3.2.2. Эллипс
|
Каноническое уравнение:
Полуоси эллипса: |
 |
|||
|
Эксцентриситет: |
 . . |
Параметрическое уравнение: | 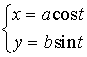 . . |
|
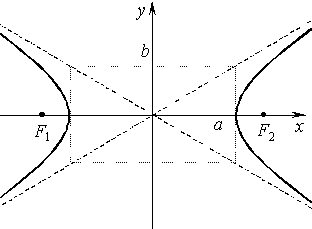
3.2.3. Гипербола
| Каноническое уравнение:
Действительная полуось: a, мнимая полуось: |
 |
|
|
Эксцентриситет: |
Асимптоты: |
Параметрическое |
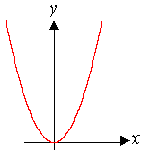
3.2.4. Парабола
| Каноническое уравнение:
Параметр: p. |
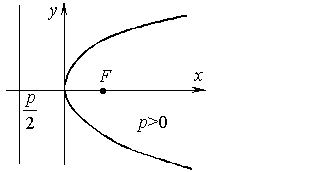 |
3.3. Поверхности второго порядка
|
Каноническое уравнение |
Наименование |
Параметры |
Чертеж |
|
|
сфера |
a – |
 |
|
|
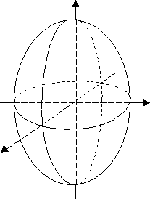
эллипсоид |
|
 |
|
|
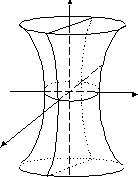
однополостный гиперболоид |
|
 |
|
|
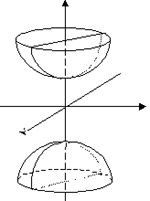
двуполостный гиперболоид |
|
 |
|
|
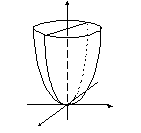
эллиптический параболоид |
|
 |
|
|
гиперболический параболоид |
|
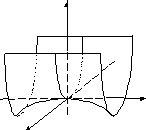 |
|
|
конус |
|
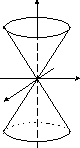 |
|
|
параболический цилиндр |
р - параметр |
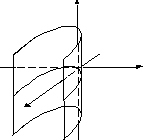 |
|
|
эллиптический цилиндр |
|
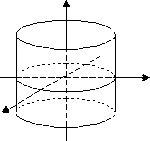 |
|
|
гиперболический цилиндр |
|
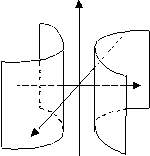 |
3.4. Преобразование координат
3.4.1. Преобразование координат на плоскости
Преобразование декартовой прямоугольной системы координат.
Параллельный перенос: 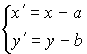 , ,
|
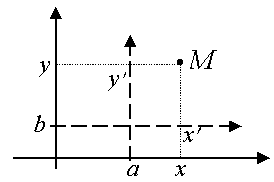 |
где координаты точки M в старой системе координат: ![]() ;
;
координаты точки M в новой системе координат: ![]() ;
;
координаты нового начала координат: ![]() .
.
Поворот: 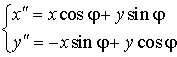 , ,
|
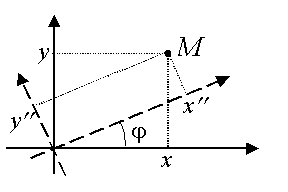 |
где координаты точки M в старой системе координат: ![]() ;
;
координаты точки M в новой системе координат: ![]() ;
;
угол поворота: j .
| Переход от декартовых прямоугольных координат 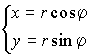 ; ; |
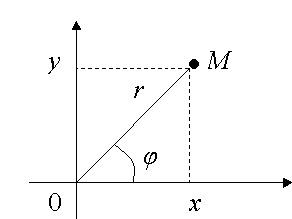 |
3.4.2. Преобразование координат в пространстве
Переход от декартовых координат ![]() к цилиндрическим координатам
к цилиндрическим координатам ![]() и обратно:
и обратно:
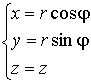 |
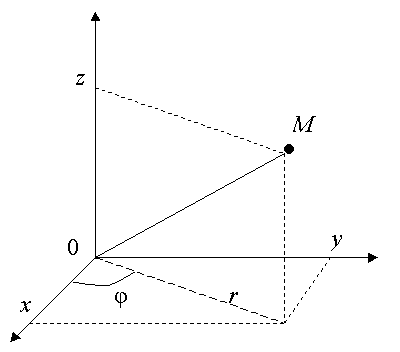 |
Переход от декартовых координат ![]() к сферическим координатам
к сферическим координатам ![]() и обратно:
и обратно:
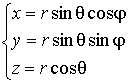 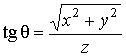 ; ; |
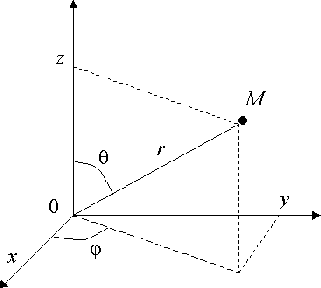 |
4. Комплексные числа
Мнимая единица ![]() .
.
4.1. Алгебраическая форма комплексного числа
![]() , где a, b – действительные числа; a - действительная часть комплексного числа, b - мнимая часть комплексного числа;
, где a, b – действительные числа; a - действительная часть комплексного числа, b - мнимая часть комплексного числа;
Обозначения действительной и мнимой части: ![]() .
.
Модуль комплексного числа: ![]() .
.
Сопряжённые комплексные числа: ![]() и
и ![]() .
.
4.2. Действия над комплексными числами в алгебраической форме
![]() ;
;
![]() ;
;
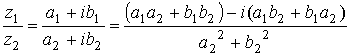 .
.
4.3. Тригонометрическая форма комплексного числа
![]() ,
,
где ![]() - аргумент комплексного числа,
- аргумент комплексного числа, ![]() .
.
4.4. Показательная форма комплексного числа
![]() .
.
Формула Эйлера: ![]() .
.
4.5. Действия над комплексными числами в тригонометрической и показательной форме
![]() ,
,
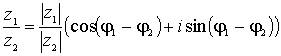 ,
,
![]() , где
, где ![]() .
.
Формула Муавра: ![]() .
.
5. Введение в анализ
5.1. Функции. Общие свойства
Числовая функция определена на множестве D действительных чисел, если каждому значению переменной ![]() поставлено в соответствие некоторое вполне определенное действительное значение переменной y, где D – область определения функции.
поставлено в соответствие некоторое вполне определенное действительное значение переменной y, где D – область определения функции.
Аналитическое представление функции:
в явном виде: ![]() ;
;
в неявном виде: ![]() ;
;
в параметрической форме: 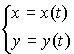 ;
;
разными формулами в области определения (a,c]: 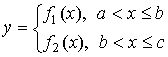 .
.
Четная функция: ![]() .
.
Нечетная функция: ![]() .
.
Периодическая функция: ![]() , где T – период функции,
, где T – период функции, ![]() .
.
5.2. Основные элементарные функции
|
Название |
Формула |
Частные случаи |
|
|
1 |
Постоянная | ||
|
2 |
Степенная функция |
|
|
|
3 |
Показательная функция | ||
|
4 |
Логарифмическая функция | ||
|
5 |
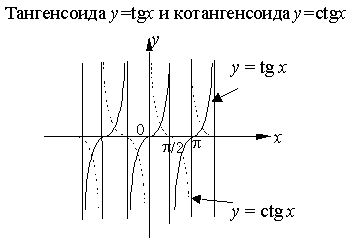
Тригонометрические функции |
|
|
|
6 |
Обратные тригонометрические функции |
|
Графики основных элементарных функций:
|
Парабола
|
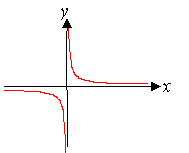
Гипербола
|
|
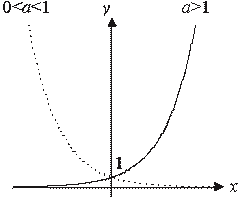
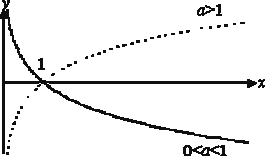
График показательной функции
|
График логарифмической фунгкции
|
|
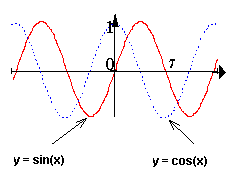
Синусоида
|
|
|
|
|
5.3. Теория пределов
Пределом функции ![]() при
при ![]() называется число b, если для любого
называется число b, если для любого ![]() (e -сколь угодно малое положительное число) можно найти такое значение аргумента
(e -сколь угодно малое положительное число) можно найти такое значение аргумента ![]() ,
,
начиная с которого выполняется неравенство ![]() .
.
Обозначение: ![]() .
.
Пределом функции ![]() при
при ![]() называется число b, если для любого
называется число b, если для любого ![]() (e -сколь угодно малое положительное число) существует такое положительное число d , что для всех значений x, удовлетворяющих неравенству
(e -сколь угодно малое положительное число) существует такое положительное число d , что для всех значений x, удовлетворяющих неравенству ![]() выполняется неравенство
выполняется неравенство ![]() .
.
Обозначение:
![]() .
.
Формула для вычисления предела элементарной функции ![]() в точке
в точке ![]() , где
, где ![]() :
: ![]() .
.
Бесконечно малая величина при ![]() есть функция
есть функция ![]() такая, что
такая, что ![]() .
.
Бесконечно большая величина при ![]() есть функция
есть функция ![]() такая, что
такая, что ![]() .
.
Первый замечательный предел: ![]() .
.
Следствия: ![]() ;
; ![]() ;
;
Второй замечательный предел: 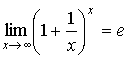 , где e=2,71828…
, где e=2,71828…
Следствия: ![]() ;
; ![]() ;
; 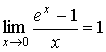 ;
; 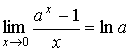 .
.
Эквивалентные бесконечно малые величины при ![]() :
:
x ~sinx ~ tgx
~ arcsinx ~
arctgx ~
ex-1~ ln(1+x).
Виды неопределенностей:
|
Символическое обозначение |
Содержание неопределенности |
Пределы компонент при x ® a |
|
|
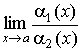 |
a 1(x) a 2(x) |
|
|
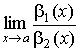 |
b 1(x) b 2(x) |
|
|
a b |
|
|
|
b 1(x) b 2(x) |
|
|
|
g b |
|
|
|
a 1(x) a 2(x) |
|
|
|
a b |
5.4. Непрерывность функции
Функция ![]() непрерывна в точке
непрерывна в точке ![]() , где
, где ![]() , если предел функции при стремлении аргумента к a, существует и равен значению функции в этой точке.
, если предел функции при стремлении аргумента к a, существует и равен значению функции в этой точке.
Эквивалентные условия:
-
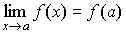 ;
;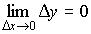 ,
,
где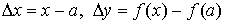 ;
;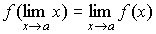 ;
;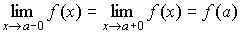 .
.
Классификация точек разрыва:
разрыв I рода:
- устранимый – односторонние пределы существуют и равны;
- неустранимый (скачок) – односторонние пределы не равны;
разрыв II рода: предел функции в точке не существует.
6. Дифференциальное исчисление
6.1. Определение производной
Пусть ![]() - определена и непрерывна в окрестности x0
- определена и непрерывна в окрестности x0
Производная функции в точке x0 и ее обозначения:
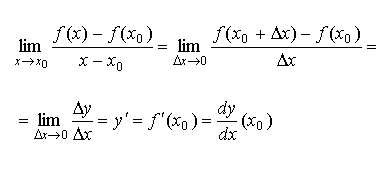
6.2. Основные правила дифференцирования
|
Наименование |
Функция |
Производная |
| Линейная комбинация двух функций
Частные случаи: a) умножение б) сумма (разность) двух функций |
|
|
| Произведение
а) двух функций б) трех функций |
|
|
| Частное двух функций |
|
|
| Сложная функция |
y=F(u), u=j (x) |
|
| Обратная функция |
|
|
| Параметрическое задание функции |
|
|
| Логарифмическое дифференцирование |
|
|
6.3. Производные основных элементарных функций
|
№ п/п |
Наименование функции |
Функция и её производная |
|
1 |
константа | |
|
2 |
степенная функция
частные случаи |
|
|
3 |
показательная функция
частный случай |
|
|
4 |
логарифмическая функция
частный случай |
|
|
5 |
тригонометрические функции | |
|
6 |
обратные тригонометрические функции |
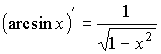 ; ;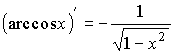 ; ;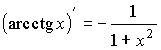 |
6.4. Гиперболические функции
|
Наименование |
Формула |
Производная |
| Гиперболический синус | 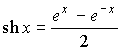 |
|
| Гиперболический косинус формула | 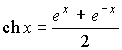 |
|
| Гиперболический тангенс | 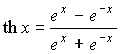 |
|
| Гиперболический котангенс | 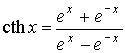 |
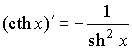 |
Обратные гиперболические функции
|
Наименование |
Формула |
Производная |
| Ареасинус | 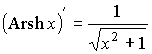 |
|
| Ареакосинус | 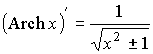 |
|
| Ареатангенс | 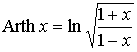 |
|
| Ареакотангенс | 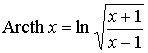 |
Графики гиперболических функций:
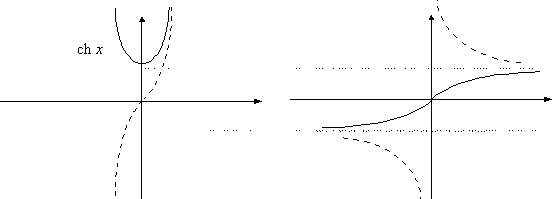
6.5. Производные высших порядков и формула Тейлора
Производная второго порядка функции y=f(x) : 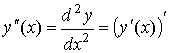
Производная n-го порядка (n-ая производная) функции y=f(x):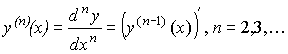
Формула Тейлора:
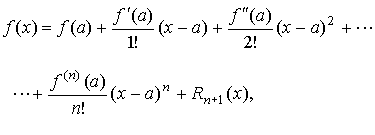
где 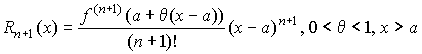
- остаточный член в форме Лагранжа.
Формула Маклорена (a=0):
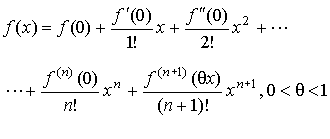
6.6. Исследование функций
План полного исследования функции:
1. Элементарное исследование:
- найти область определения и область значений;
- выяснить общие свойства: четность(нечетность), периодичность;
- найти точки пересечения с осями координат;
- определить участки знакопостоянства.
2. Исследование с помощью предела:
- найти точки разрыва и выяснить их характер;
- найти область непрерывности;
- найти вертикальные и наклонные асимптоты.
3. Исследование с помощью
:
- найти критические точки;
- определить интервалы возрастания и убывания функции;
- определить экстремумы.
4. Исследование с помощью
:
- найти точки, в которых
или не существует;
- найти участки выпуклости и вогнутости;
- определить точки перегиба.
5. Построение графика функции.
Рекомендации по применению плана исследования функции:
- Отдельные элементы исследования наносятся на график постепенно, по мере их нахождения.
- Если появляются затруднения с построением графика функции, то находятся значения функции в некоторых дополнительных точках.
- Целью исследования является описание характера поведения функции. Поэтому строится не точный график, а его приближение, на котором четко обозначены найденные элементы (экстремумы, точки перегиба, асимптоты и т.д.).
- Строго придерживаться приведенного плана необязательно; важно не упустить характерные элементы поведения функции.
7. Интегральное исчисление
7.1. Неопределенный интеграл
7.1.1. Определения и свойства
Функция ![]() называется первообразной для
называется первообразной для ![]() , если
, если ![]() .
.
Неопределенным интегралом от функции f(x) называется совокупность всех первообразных для этой функции.
Обозначение: ![]() , где
, где ![]() - произвольная постоянная.
- произвольная постоянная.
Свойства неопределенного интеграла
-
- Производная неопределенного интеграла:
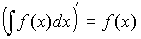 .
. - Дифференциал неопределенного интеграла:
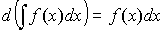 .
. - Неопределенный интеграл от дифференциала:
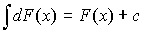 .
.
- Производная неопределенного интеграла:
- Неопределенный интеграл от линейной комбинации функций:
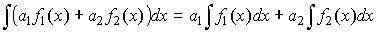 ;
;
4а. Неопределенный интеграл от суммы (разности) двух функций:![]() ;
;
4б. Вынесение постоянного множителя за знак неопределенного интеграла:![]()
7.1.2. Основные методы интегрирования
-
- использование свойств неопределенного интеграла;
- подведение под знак дифференциала;
- метод замены переменной:
а) замена ![]() в интеграле
в интеграле ![]() :
: ![]()
![]() где
где ![]() - функция, интегрируемая легче, чем исходная;
- функция, интегрируемая легче, чем исходная; ![]() - функция, обратная функции
- функция, обратная функции ![]() ;
; ![]() - первообразная функции
- первообразная функции ![]() ;
;
б) замена ![]() в интеграле вида
в интеграле вида ![]() :
:
![]()
![]() ;
;
-
- метод интегрирования по частям:
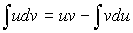 .
.
- метод интегрирования по частям:
7.1.3. Таблица интегралов
- Степенная функция
частные случаи
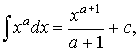
![]()
![]() ,
, ![]()
2. Показательная функция
частный случай
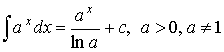
![]()
3. Рациональные функции
![]()
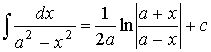
4. Иррациональные функции
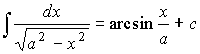
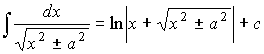
5. Тригонометрические функции
![]()
![]()
![]()
![]()
6. Содержит тригонометрические функции
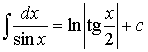
![]()
![]()
7.2. Определенный интеграл
7.2.1. Определения и свойства
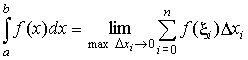 ,
,
где ![]()
Свойства определенного интеграла
-
- Интеграл от суммы или разности двух функций:
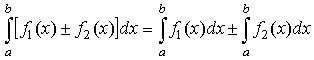 .
.
- Интеграл от суммы или разности двух функций:
- Внесение или вынесение постоянного множителя за знак интеграла:
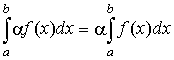 .
.
- Свойство аддитивности:
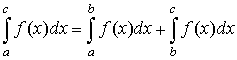 .
. - Неотрицательность интеграла: если
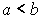 ,
,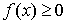 , то
, то 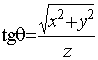 .
. - Сохранение неравенства: если
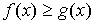 и
и 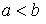 , то
, то 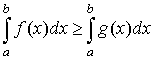 .
. - Теорема о среднем:
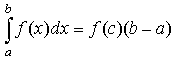 , где
, где 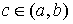 ,
, 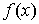 - непрерывна на
- непрерывна на 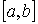 .
. - Формула Ньютона-Лейбница:
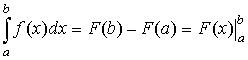 , где
, где 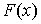 - первообразная для
- первообразная для 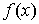 .
. - Интегрирование по частям:
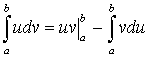 .
. - Замена переменной:
а) 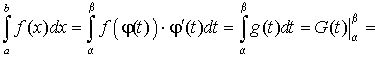
![]() , где
, где ![]() ,
, ![]() ,
, ![]() и
и ![]() непрерывна на
непрерывна на ![]() , а
, а ![]() непрерывна и монотонна на
непрерывна и монотонна на ![]()
б) 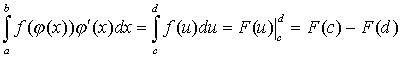 , где u=j (x), c=j (a), d=j (b).
, где u=j (x), c=j (a), d=j (b).
7.2.2. Приложения определенного
интеграла
|
Характеристика |
Вид функции |
Формула |
| площадь криволинейной трапеции | в декартовых координатах | 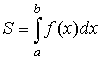 |
| площадь криволинейного сектора | в полярных координатах | 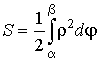 |
| площадь криволинейной трапеции | в параметрической форме | 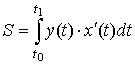 |
| длина дуги кривой | в декартовых координатах | 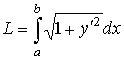 |
| длина дуги кривой | в полярных координатах | 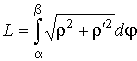 |
| длина дуги кривой | в параметрической форме | 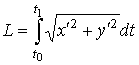 |
| объём тела вращения | в декартовых координатах | 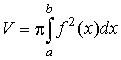 |
| объём тела с заданным поперечным сечением | 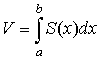 |


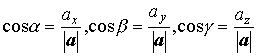
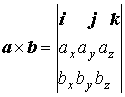
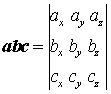
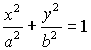 .
.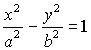 .
.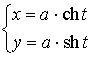
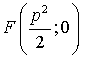 ;
;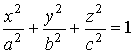 .
.