Источник дискретных сообщений характеризуется совокупностью возможных элементов сообщения и вероятностями появления этих элементов на выходе источника . В передающем устройстве сообщение преобразовывается в сигнал таким образом, что каждому элементу сообщения соответствует определенный сигнал. Обозначим эти сигналы через , a их вероятности появления на выходе передатчиков (априорные вероятности) соответственно через . Очевидно, априорные вероятности сигналов P(s) равны априорным вероятностям P(u) соответствующих сообщений . В процессе передачи на сигнал накладывается помеха. Пусть эта помеха имеет равномерный спектр мощности с интенсивностью

Тогда сигнал на входе можно представить как сумму переданного сигнала S(t) и помехи w (t):

Поскольку сигналы x(t) и помеха (t) заданы на конечном интервале (0<t<Т), то согласно (2.70) их можно представить в виде разложений по ортогональным функциям:

(5.18)

(5.19)

(5.20)

где

(5.21)

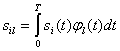(5.22)

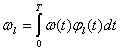(5.23)

Так как мы предполагаем, что помеха имеет нормальное распределение, то и коэффициенты Фурье в выражении (5.23) будут иметь нормальное распределение с дисперсией и средним значением, равным нулю:

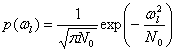(5.24)

Коэффициенты x также имеют нормальное распределение с той же дисперсией и средним значением

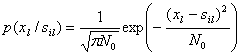(5.25)

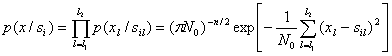(5.26)

В силу независимости коэффициентов многомерное распределение коэффициентов хт. е. условное распределение p(x/s), будет равно произведению одномерных распределений (5.25):

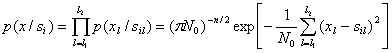(5.26)

Подставляя это выражение в (5.5), получим следующее неравенство, определяющее условие оптимального приема по Котельникову:

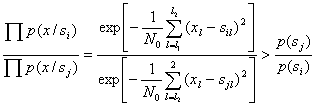(5.27)

Логарифмируя обе части неравенства, приходим к эквивалентному выражению

(5.28)

В соответствии с выражениями (5.20) и (5.18) имеем

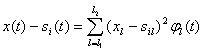(5. 29)

После возведения в квадрат и усреднения по времени выражения (5.29) с учетом свойств ортогональных функций (t) (2.55) получаем

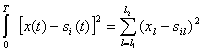(5.30)

Тогда условие оптимального приема (5.28) можно записать в другом виде:

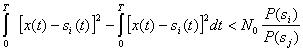(5.31)

Неравенства (5.27) или им эквивалентные неравенства (5.28) и (5.31) определяют условия правильного приема сигнала s(t). В случае, когда априорные вероятности сигналов одинаковы

— , критерий Котельникова принимает более простой вид:

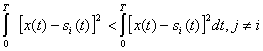(5.32)

Отсюда следует, что при равновероятных сигналах оптимальный приемник воспроизводит сообщение, соответствующее тому переданному сигналу, который имеет наименьшее среднеквадратичное отклонение от принятого сигнала.

Неравенство (5.32) можно записать в другом виде, раскрыв скобки:

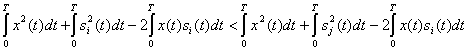
00

Для сигналов, энергии которых одинаковы, это неравенство для всех принимает более простую форму:

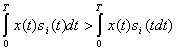(5.33)

В этом случае условие оптимального приема можно сформулировать следующим образом. Если все возможные сигналы равновероятны и имеют одинаковую энергию, оптимальный приемник воспроизводит сообщение, соответствующее тому переданному сигналу, взаимная корреляция которого с принятым сигналом максимальна.

Для двоичной системы полученным результатам можно дать весьма наглядную геометрическую трактовку. Пусть передаются два равновероятных сообщения ии u2 с помощью сигналов и s2. Первому сигналу соответствует вектор в n-мерном пространстве, а второму — вектор s2. Принятому сигналу соответствует вектор х, равный сумме векторов сигнала s и помехи w. Пространство возможных значений сигнала можно разбить на две области так, чтобы при попадании конца вектора х в первую область воспроизводился сигнал (область сигнала ) а при попадании в другую область — воспроизводился сигнал s2 (область сигнала s2). Если х, соответствующий данному сигналу, попадает в область другого сигнала, то происходит ошибка (вместо s\ воспроизводится s2 или, наоборот, s2 вместо s1). Вероятность ошибки, очевидно, зависит от конфигурации областей сигнала. В оптимальном приемнике Котельникова пространство сигналов разбивается на области сигнала si и сигнала s2 так, чтобы полная вероятность ошибки (5.13) была минимальной.

В случае равновероятных сигналов и помехи с равномерным распределением оптимальным разбиением пространства будет такое, при котором любая точка х относится к области того сигнала s, конец вектора которого ближе всего к точке х. В двухмерной модели (рис. 5.3) для двоичной системы граница областей сигналов и s2 есть геометрическое место точек, равноотстоящих от и s2, т. е. гиперплоскость, перпендикулярная к вектору разности и делящая его пополам.

Если, например, передавался сигнал , то ошибка произойдет в том случае, когда выполняется неравенство

(5.34)

Или

(5.35)

где , и — проекция w на вектор, коллинеарный s, т. е.

.Вместо неравенства (5.34) можно записать или в эвклидовой метрике

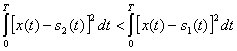(5.36)

Условие (5.36) полностью совпадает с условием (5.32). Структурная схема приемника, реализующего операции (5.36), приведена на рис. 5.4. Здесь Г и Г2 — генераторы опорных сигналов, формирующие точные копии переданных сигналов s1 и s2, В — вычитающее устройство, KB — квадратирующее устройство, И — интегратор, РУ — схема сравнения и выбора (решающее устройство).

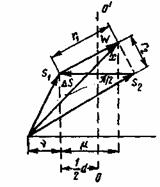
Рис. 5.3. Геометрическое представление работы оптимального приемника

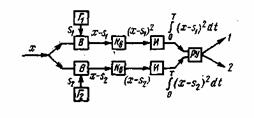
Рис. 5.4. Оптимальный приемник Котельникова

Неравенство (5.36) можно записать в другом виде, раскрыв скобки под интегралами:

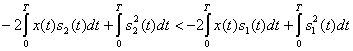
или

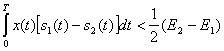(5.37)

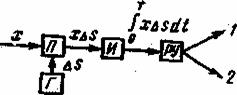
Рис. 5.5. Оптимальный пороговый приемник

Это неравенство совершенно эквивалентно неравенству (5.36), но оно ведет к другой схемной реализации оптимального приемника.

На рис. 5.5 приведена структурная схема приемника, реализующего условия работы (6.37). В этой схеме после операции перемножения (П) и интегрирования (И) производится сравнение полученного результата с постоянным порогом, равным разности энергий сигналов

Эта схема проще, чем схема рис. 5.4. Однако она обладает тем недостатком, что при изменении уровня сигналов порог нужно автоматически регулировать. Этот недостаток устраняется, если сигналы имеют равную энергию E2=E, тогда порог равен нулю и решающая схема определяет только знак сигнала на выходе.

При упрощается и схема приемника рис. 5.4. Раскрывая скобки в (5.36), получаем условия оптимального приема в следующем виде:

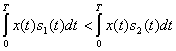(5.38)

что совпадает с условием (5.33). Таким образом, при приемник Котельникова превращается в корреляционный (когерентный) (рис. 5.6).

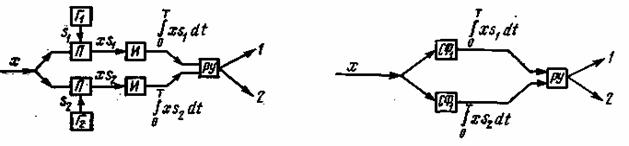
Рис. 5.6. Корреляционный приемник Рис. 5.7. Приемник с согласованными фильтрами

Оптимальный прием можно также реализовать в схеме с согласованными линейными фильтрами (рис. 5.7), импульсные реакции которых должны быть , где с — постоянный коэффициент (см. § 4.6).

Рассмотренные схемы оптимальных приемников относятся к типу когерентных, в них учитывается не только амплитуда, но и фаза высокочастотного сигнала.

Заметим, что в схемах оптимальных приемников отсутствуют фильтры на входе, которые в реальных приемниках всегда имеются. Это означает, что оптимальный приемник при флуктуационных помехах не требует фильтрации на входе. Его помехоустойчивость, как мы увидим дальше, не зависит от ширины полосы пропускания приемника.