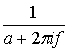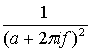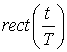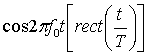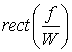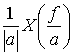А.1. Сигналы, спектры и линейные системы
А.2. Применение методов Фурье к анализу линейных систем
А.3. Свойства преобразования Фурье
А.5.1. Графическая иллюстрация свертки
А.1. Сигналы, спектры и линейные системы
Электрические сигналы связи — это меняющиеся со временем сигналы напряжения или тока, обычно описываемые во временной области. С другой стороны, подобные сигналы также удобно описывать в частотной области, где описание сигнала называется его спектром. Спектральные понятия достаточно важны при анализе и проектировании систем связи; они могут описывать сигнал через его среднюю мощность или энергетическое содержание на различных частотах и показывают, какую часть (полосы) электромагнитного спектра занимает сигнал. Федеральная комиссия по средствам связи США (Federal Communications Commission — FCC) требует, чтобы теле- и радиостанции работали на выделенных им частотах при крайне малых промежутках между полосами, занятыми различными станциями. Например, амплитудно-модулированные радиоканалы разделены полосой 10 кГц, а телевизионные каналы — полосой 6 МГц. Так что наш интерес к спектрам и анализу Фурье объясняется реальными требованиями помещения сигнала в точно заданные границы.
Частотные спектральные характеристики можно приписать как к собственно сигналам, так и электрическим схемам. Если говорится, что конкретный спектр описывает сигнал, подразумевается, что один из способов описания сигнала — это задать его амплитуду и фазу как функции частоты. В то же время, когда мы говорим о спектральных параметрах схемы, имеем в виду передаточную функцию (или частотную характеристику), связывающую выход схемы с ее входом; другими словами, схема характеризуется тем, какая часть спектра входного сигнала пройдет на выход.
А.2. Применение методов Фурье к анализу линейных систем
Методы Фурье используются для анализа линейных схем или систем: (1) для предсказания реакции (отклика) системы; (2) для определения динамики системы (передаточной функции) и (3) для оценки или интерпретации результатов тестов. Предсказание реакции системы (1) схематически проиллюстрировано на рис. А.1. Пусть на вход системы подается произвольный периодический сигнал с периодом Т0секунд. Методы Фурье-анализа, как показано на рисунке, позволяют описать подобный вход как сумму синусоидальных сигналов. Наименьшая (или собственная) частота этих сигналов — 1/Т Гц; остальные частоты кратны данной (2/Т0, 3/Т0, ...) и называются гармониками. Важной особенностью линейной системы является принцип суперпозиции — реакция на сумму сигналов равна сумме откликов на каждый сигнал. Фактически это свойство используется как определение линейности. Математически система линейна, если для всех a, b, x1(t) и х2(t)
y1(t) — реакция системы на x1(t);
y2(t) — реакция системы на x2(t);
ay1(t) + by2(t) — реакция системы на ax1(t) + bx2(t).
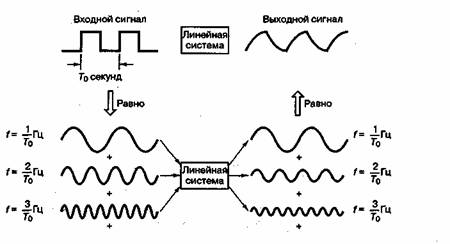
Рис. А. 1. Предсказание реакции системы
Данное определение свидетельствует о том, что выходной отклик линейной системы с входными синусоидальными сигналами должен составляться из синусоидальных сигналов с теми же частотами, что и у входных сигналов; обычно подобная система задается частотной передаточной функцией (частотной характеристикой), описывающей изменение амплитуды и фазы сигнала в зависимости от частоты, как показано на рис. А.2. На рис. А.2, а представлена характерная зависимость амплитуды сигнала от частоты; подобным образом на рис. А.2, б показана зависимость фазы сигнала от частоты.
Передаточная функция является рабочей характеристикой системы, т.е. описывает отклик системы на каждую синусоиду. Следовательно, имея передаточную функцию системы, можно предсказать каждый выходной компонент. С помощью принципа суперпозиции эти выходные компоненты суммируются, что дает реакцию системы на любой входной сигнал (рис. А.1). Подобным образом, зная входной и выходной сигналы, можно определить передаточную функцию системы.
Развитие методов Фурье-анализа оказало большое влияние на анализ линейных систем; оно позволило связать переходные процессы и методы работы с гармоническими функциями, а также упростило анализ линейных систем при их активизации произвольным входным сигналом. Как логарифм позволяет превратить операцию умножения в операцию сложения, так и методы Фурье-анализа позволяют заменить сложные сигналы гармоническими составляющими и методами работы с гармоническими функциями.
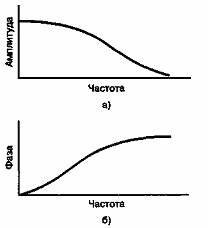
Рис. А.2. Передаточная функция системы:
а) амплитудная характеристика;
б) фазовая характеристика
А.2.1. Разложение в ряд Фурье
Периодические сигналы с конечной энергией, передаваемой за период, можно представить в виде ряда Фурье. Произвольный периодический сигнал x(![]() ) выражается через бесконечное число гармоник с возрастающими частотами.
) выражается через бесконечное число гармоник с возрастающими частотами.
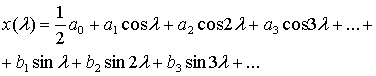 (А.1)
(А.1)
Члены cos![]() и sin
и sin![]() , называются основными; члены cos n
, называются основными; члены cos n![]() и sin n
и sin n![]() при n > 1, где п — целое, именуются гармоническими. Члены апи bn представляют коэффициенты гармоник, а
при n > 1, где п — целое, именуются гармоническими. Члены апи bn представляют коэффициенты гармоник, а ![]()
![]() — это постоянный член или составляющая постоянного тока.
— это постоянный член или составляющая постоянного тока.
Период функции х(![]() ) должен равняться 2
) должен равняться 2![]() или кратной величине; кроме того, функция х(
или кратной величине; кроме того, функция х(![]() ) должна быть однозначной. Ряд Фурье можно рассматривать как «рецепт приготовления» любого периодического сигнала из синусоидальных составляющих. Чтобы данный ряд имел практическое значение, он должен сходиться, т.е. частичные суммы ряда должны иметь предел.
) должна быть однозначной. Ряд Фурье можно рассматривать как «рецепт приготовления» любого периодического сигнала из синусоидальных составляющих. Чтобы данный ряд имел практическое значение, он должен сходиться, т.е. частичные суммы ряда должны иметь предел.
Процесс создания произвольного периодического сигнала из коэффициентов, описывающих смешивание гармоник, называется синтезом. Обратный процесс вычисления коэффициентов именуется анализом. Вычисление коэффициентов облегчается тем, что среднее от перекрестных произведений синусоиды на косинусоиду (а также средние любой синусоиды или косинусоиды) равно нулю. Ниже приводятся формулы, иллюстрирующие основные свойства средних от гармонических функций.
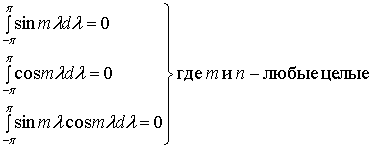 (А.2)
(А.2)
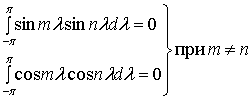 (А.3)
(А.3)
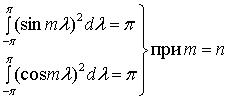 (А.4)
(А.4)
Рассмотрим, как вычисляются значения коэффициентов аn или bn в формуле (А.1). Например, для вычисления коэффициента а3 обе стороны формулы (А. 1) можно умножить на cos 3![]() d
d![]() , а затем проинтегрировать.
, а затем проинтегрировать.
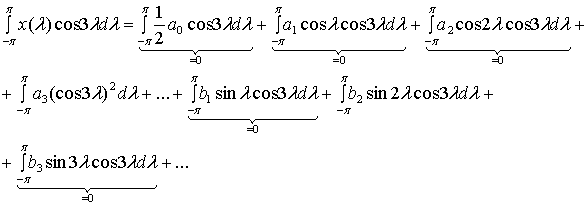
![]()
![]()
Полученный вывод можно обобщить.
![]() (A.5)
(A.5)
![]() (А.6)
(А.6)
Коэффициент а0 находится из (А.5) при n = 0. В результате получаем следующее.
![]() (A.7)
(A.7)
Данное выражение — это член нулевой частоты, или среднее значение периодического сигнала. Процесс синтеза уравнения (А.1) можно записать в более компактной форме.
![]() (A.8)
(A.8)
Существует несколько способов выражения пары преобразований (анализа и синтеза) Фурье. Наиболее распространенная форма - это выражение синуса и косинуса через экспоненты с комплексным показателем.
![]() (А.9)
(А.9)
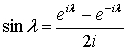 (А.10)
(А.10)
Периодическая функциях c периодом Т0секунд имеет следующие частотные компоненты — ![]() ,
, ![]() ,
, ![]() , ..., где f0 = 1/Т0называется собственной частотой. Иногда частотные компоненты записывают как
, ..., где f0 = 1/Т0называется собственной частотой. Иногда частотные компоненты записывают как ![]() , 2
, 2![]() , 3
, 3![]() , …, где
, …, где ![]() именуется собственной угловой частотой; частота f измеряется в герцах, частота w — в радианах в секунду. Заменим п
именуется собственной угловой частотой; частота f измеряется в герцах, частота w — в радианах в секунду. Заменим п![]() в аргументах гармонических функций в формулах (А.5)-(А.8) на
в аргументах гармонических функций в формулах (А.5)-(А.8) на ![]() , где n- целое. При n = 1, пf0 представляет собственную частоту, а при п>1 - гармоники собственной частоты. Используя формулы (А.8)-(А.10), можно записать x(t) в экспоненциальной форме.
, где n- целое. При n = 1, пf0 представляет собственную частоту, а при п>1 - гармоники собственной частоты. Используя формулы (А.8)-(А.10), можно записать x(t) в экспоненциальной форме.
![]() (A.11)
(A.11)
Обозначим через спкомплексные коэффициенты, или спектральные компоненты x(t), связанные с коэффициентами апи bn следующим образом.
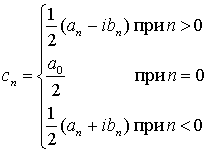 (A.12)
(A.12)
Теперь формулу (А. 11) можно упростить.
![]() (A.13)
(A.13)
Здесь коэффициенты экспоненциальных гармоник определяются следующим образом.
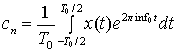 (A. 14)
(A. 14)
Для проверки справедливости формулы (А. 14) умножим обе части выражения (А. 13) на![]() , проинтегрируем по промежутку (
, проинтегрируем по промежутку (![]() ) и используем следующую формулу.
) и используем следующую формулу.
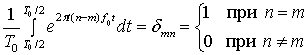 (А.15)
(А.15)
Здесь ![]() называется дельта-функцией Кронекера. После выполнения указанных действий получаем
называется дельта-функцией Кронекера. После выполнения указанных действий получаем
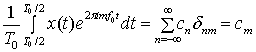 (A.16)
(A.16)
для всех целых т. В общем случае коэффициент сn - комплексное число, выразить которое можно следующим образом.
![]() (А.17)
(А.17)
![]() ,
,![]() (А.18)
(А.18)
где
![]() (А.19)
(А.19)
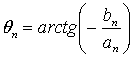 (А.20)
(А.20)
Значение |сn| определяет амплитуду n-й гармоники периодического сигнала, так что график зависимости |сn| от частоты, называемой амплитудным спектром, дает амплитуду каждой из n дискретных гармоник сигнала. Подобным образом график зависимости ![]() от частоты, именуемой фазовым спектром, дает фазу каждой гармоники сигнала. Коэффициенты Фурье вещественной периодической по времени функции обладают следующим свойством.
от частоты, именуемой фазовым спектром, дает фазу каждой гармоники сигнала. Коэффициенты Фурье вещественной периодической по времени функции обладают следующим свойством.
![]() (А.21)
(А.21)
где ![]() — комплексно сопряженное сn. Таким образом, получаем следующее.
— комплексно сопряженное сn. Таким образом, получаем следующее.
![]() (А.22)
(А.22)
Амплитудный спектр является четной функцией частоты. Подобным образом фазовый спектр ![]() — это нечетная функция частоты, поскольку из формулы (А.20) следует, что
— это нечетная функция частоты, поскольку из формулы (А.20) следует, что
![]() . (А.23)
. (А.23)
Итак, как отмечалось выше, ряды Фурье особенно полезны при описании произвольных периодических сигналов с конечной энергией каждого периода. Кроме того, они могут использоваться для описания непериодических сигналов, имеющих конечную энергию за конечный интервал. Впрочем, для таких сигналов более удобным является представление в виде интеграла Фурье (см. раздел А.2.3).
А.2.2. Спектр последовательности импульсов
В цифровой связи весьма важным сигналом является идеальная периодическая последовательность прямоугольных импульсов, показанная на рис. А.З. Для коэффициентов ряда Фурье последовательности импульсов xp(t) с периодом T0 (каждый импульс имеет амплитуду А и длительность T) справедливо следующее выражение (проверить справедливость можно с помощью формул (А. 14) и (А.10)).
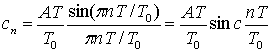 (A.24)
(A.24)
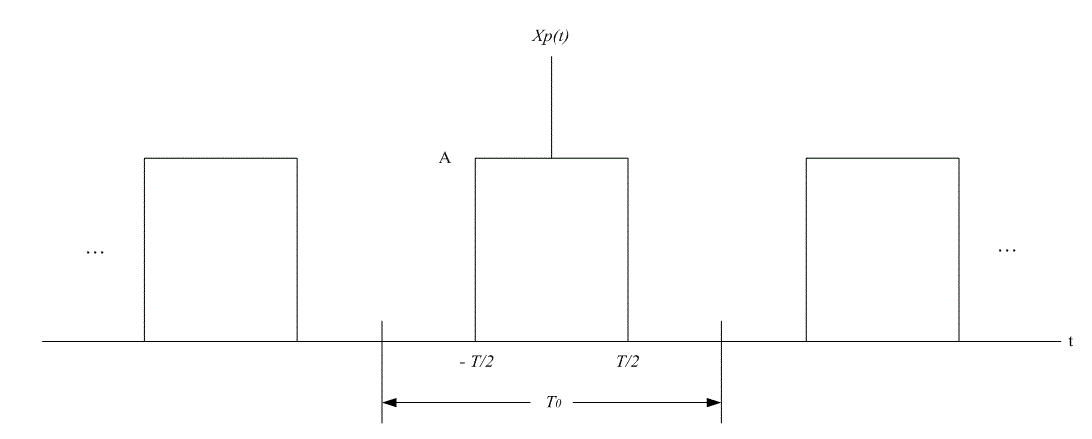
Рис. А.З. Последовательность импульсов
В данном выражении
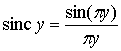
Функция sinc, как показано на рис. А.4, достигает максимума (единицы) при у=0 и стремится к нулю при у![]() , осциллируя с постепенно уменьшающейся амплитудой. Через нуль она проходит в точках у = ±1, ±2, .... На рис. А.5, а как функция отношения п/Т0показан амплитудный спектр последовательности импульсов |сп|, а на рис. А.5, б изображен фазовый спектр
, осциллируя с постепенно уменьшающейся амплитудой. Через нуль она проходит в точках у = ±1, ±2, .... На рис. А.5, а как функция отношения п/Т0показан амплитудный спектр последовательности импульсов |сп|, а на рис. А.5, б изображен фазовый спектр ![]() . Следует отметить, что положительные и отрицательные частоты двустороннего спектры - это весьма полезный способ математического выражения спектра; очевидно, что в лабораторных условиях воспроизвести можно только положительные частоты.
. Следует отметить, что положительные и отрицательные частоты двустороннего спектры - это весьма полезный способ математического выражения спектра; очевидно, что в лабораторных условиях воспроизвести можно только положительные частоты.
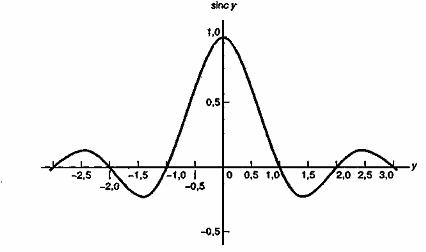
Рис. А.4. Функция sinc
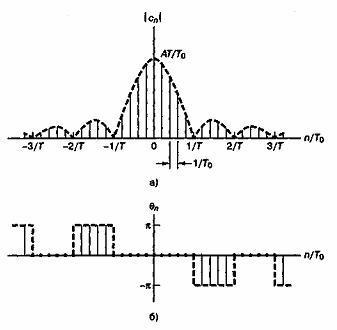
Рис. А.5. Спектр последовательности импульсов:
а) амплитудный; б) фазовый
Синтез выполняется посредством подстановки коэффициентов из формулы (А.24) в формулу (А.13). Получаемый ряд представляет исходную последовательность импульсов xр(t), синтезированную из составных элементов.
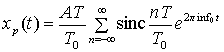 (A.25)
(A.25)
Идеальная периодическая последовательность импульсов включает все гармоники, кратные собственной частоте. В системах связи часто предполагается, что значительная часть мощности или энергии узкополосного сигнала приходится на частоты от нуля до первого нуля амплитудного спектра (рис. А.5, а). Таким образом, в качестве меры ширины полосы последовательности импульсов часто используется величина 1/Т (где Т — длительность импульса). Отметим, что ширина полосы обратно пропорциональна длительности импульса; чем меньше импульсы, тем более широкая полоса с ними связана. Отметим также, что расстояние между спектральными линиями ![]() обратно пропорционально периоду импульсов; при увеличении периода линии располагаются ближе друг к другу.
обратно пропорционально периоду импульсов; при увеличении периода линии располагаются ближе друг к другу.
А.2.3. Представление в виде интеграла Фурье
В системах связи часто встречаются непериодические сигналы, имеющие конечную энергию в конечном интервале и нулевую энергию за пределами этого интервала. Подобные сигналы удобно описывать, используя представление в виде интеграла Фурье, или просто Фурье-образ. Непериодический сигнал можно описать как периодический в предельном смысле. Рассмотрим, например, последовательность импульсов, показанную на рис. А.З. Если Т0стремится к бесконечности, последовательность импульсов превращается в отдельный импульс x(t), число спектральных линий стремится к бесконечности, а график спектра превращается в гладкий спектр частот Х(f). Для данного предельного случая можно определить пару интегральных преобразований Фурье.
![]() (A.26)
(A.26)
и
![]() , (A.27)
, (A.27)
где f - частота, измеряемая в герцах. Данную пару преобразований можно использовать при описании частотно-временных соотношений непериодических сигналов.
С этого момента применение преобразования Фурье будем обозначать ![]()
![]() , а обратное преобразование —
, а обратное преобразование — ![]() . Связь частотной и временной областей будем указывать с использованием знака
. Связь частотной и временной областей будем указывать с использованием знака ![]() .
.
![]()
Данная запись означает, что X(f) получается в результате применения преобразования Фурье к x(t), а х(t) - в результате применения обратного преобразования Фурье к X(f). В контексте систем связи x(t) — вещественная функция, a X(f) — комплексная функция, имеющая действительный и мнимый компоненты; в полярной форме спектр X(f) можно задать через его амплитудную и фазовую характеристики.
![]() (А.28)
(А.28)
Свойства X(f), спектра непериодического сигнала, подобны свойствам периодического сигнала, представленным в формулах (А.17)-(А.23); т.е. если x(t) принимает вещественные значения,
![]() (А.29)
(А.29)
![]() , (А.30)
, (А.30)
где X* — комплексно сопряженное X. Амплитудный спектр |X(f)| — это четная функция f, а фазовый спектр — нечетная функция f. Во многих случаях функция X(f) имеет или только действительную часть, или только мнимую, так что для ее описания достаточно одного графика.
А.3. Свойства преобразования Фурье
Существует множество хороших справочников, в которых подробно рассмотрены преобразования Фурье и их свойства [1-4]. В данном приложении внимание акцентируется на свойствах, представляющих интерес в теории связи. Некоторыми ключевыми особенностями передач в системах связи являются временная задержка, сдвиг фазы, перемножение с другими сигналами, трансляция частоты, свертка сигнала и свертка спектра. Остановимся подробнее на свойствах преобразования Фурье (сдвиг и свертка), необходимых для описания данных особенностей.
А.3.1. Сдвиг во времени
Если ![]() , то
, то
![]() (A.31)
(A.31)
Пусть ![]() , тогда
, тогда
![]()
Если сигнал запаздывает во времени, амплитуда его частотного спектра не меняется, а фазовый спектр сдвигается по фазе. Сдвиг на время t0 во временной области эквивалентен умножению на ![]() (сдвигу фазы на
(сдвигу фазы на ![]() ) во временной области.
) во временной области.
А.3.2. Сдвиг по частоте
Если ![]() , то
, то
![]() (A.32)
(A.32)
Выше приведено свойство трансляции частоты, которое описывает смещенный спектр, возникающий при умножении сигнала на ![]() . Используя формулу (А.32) вместе с формулой (А.9), можно получить выражения для Фурье-образа сигнала, умноженного на косинусоиду.
. Используя формулу (А.32) вместе с формулой (А.9), можно получить выражения для Фурье-образа сигнала, умноженного на косинусоиду.
![]()
![]() (А.33)
(А.33)
Данное свойство также называется теоремой о модуляции (или смешивании). Умножение произвольного сигнала на синусоиду частоты f0 приводит к трансляции исходного спектра сигнала на f0 и -f0.
А.4. Полезные функции
А.4.1. Дельта-функция
Полезной функцией в теории связи является так называемая дельта-функция Дирака, или единичный импульс, ![]() . Импульсную функцию можно определить из любой фундаментальной функции (например, прямоугольного или треугольного импульса). В любом случае импульсная функция определяется в пределе (амплитуда импульса стремится к бесконечности, длительность импульса — к нулю, а площадь импульса равна единице) [5]. Единичная импульсная функция имеет следующие свойства.
. Импульсную функцию можно определить из любой фундаментальной функции (например, прямоугольного или треугольного импульса). В любом случае импульсная функция определяется в пределе (амплитуда импульса стремится к бесконечности, длительность импульса — к нулю, а площадь импульса равна единице) [5]. Единичная импульсная функция имеет следующие свойства.
![]() (А.34)
(А.34)
![]() (А.35)
(А.35)
![]() не ограничена в точке t = 0 (А.36)
не ограничена в точке t = 0 (А.36)
![]() (А.37)
(А.37)
![]() (A.38)
(A.38)
Формула (А.38) представляет просеивающее (или выборочное) свойство; результат интегрирования функции x(t) с дельта-функцией — выборка функции x(t) в точке t = t0.
В некоторых задачах полезными бывают следующие представления дельта-функции в частотной и временной областях.
![]() (А.39)
(А.39)
![]()
![]() (A.40)
(A.40)
A.4.2. Спектр синусоиды
Для нахождения Фурье-образа синусоидального сигнала Необходимо предположить, что данный сигнал существует только в интервале (![]() ). При таком условии функция будет иметь Фурье-образ, пока Т0будет конечно. В пределе Т0предполагается очень большим, но конечным. Спектр сигнала x(t) =
). При таком условии функция будет иметь Фурье-образ, пока Т0будет конечно. В пределе Т0предполагается очень большим, но конечным. Спектр сигнала x(t) =![]() можно найти, используя формулы (А.9) и (А.26).
можно найти, используя формулы (А.9) и (А.26).
![]()
Как видно из формулы (А.40), данное интегральное выражение можно записать через следующие единичные импульсные функции.
![]() (А.41)
(А.41)
Подобным образом можно показать, что спектр синусоидального сигнала ![]() равен следующему.
равен следующему.
![]() (А.42)
(А.42)
Спектр косинусоидального сигнала показан на рис. А.6, а спектр синусоидального сигнала — на рис. А.7. Все дельта-функции на этих рисунках изображены как пики с весовыми коэффициентами А/2 или -А/2.
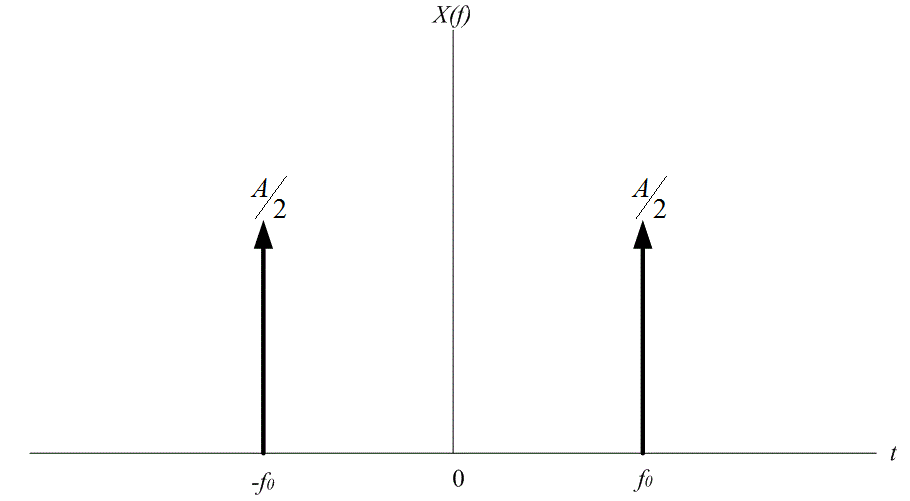
Рис. А.6. Спектр сигнала x(t) =![]()
А.5. Свертка
В конце XIX века Оливер Хевисайд (Oliver Heaviside) использовал свертку для вычисления тока на выходе электрической схемы, на вход которой подан сигнал, описываемый сложной функцией напряжения. Использование методов Хевисайда предшествовало применению аналитических методов, разработанных Фурье и Лапласом (хотя публикации Фурье и Лапласа вышли раньше).
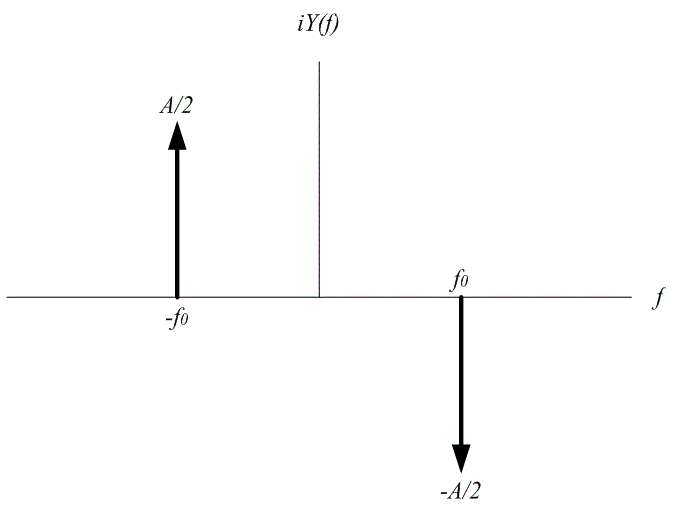
Рис. A.7. Спектр сигнала ![]()
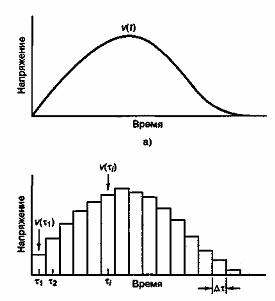
Отклик схемы на входное импульсное возмущение ![]() называется импульсной характеристикой и обозначается h(t), как показано на рис. А.8, т.е. это просто выходное напряжение, полученное при подаче на вход дельта-функции. Хевисайд аппроксимировал произвольный сигнал, подобный показанному на рис. А.9, а, набором равноотстоящих импульсов. Подобные импульсы конечной высоты и ненулевой длительности показаны на рис. А.9, б. В пределе при длительности импульса
называется импульсной характеристикой и обозначается h(t), как показано на рис. А.8, т.е. это просто выходное напряжение, полученное при подаче на вход дельта-функции. Хевисайд аппроксимировал произвольный сигнал, подобный показанному на рис. А.9, а, набором равноотстоящих импульсов. Подобные импульсы конечной высоты и ненулевой длительности показаны на рис. А.9, б. В пределе при длительности импульса ![]() каждый импульс стремится к дельта-функции с весовым коэффициентом, равным площади импульса. Далее будем считать, что данные равноотстоящие импульсы имеют нулевую длительность, хотя строго они являются такими только в пределе.
каждый импульс стремится к дельта-функции с весовым коэффициентом, равным площади импульса. Далее будем считать, что данные равноотстоящие импульсы имеют нулевую длительность, хотя строго они являются такими только в пределе.
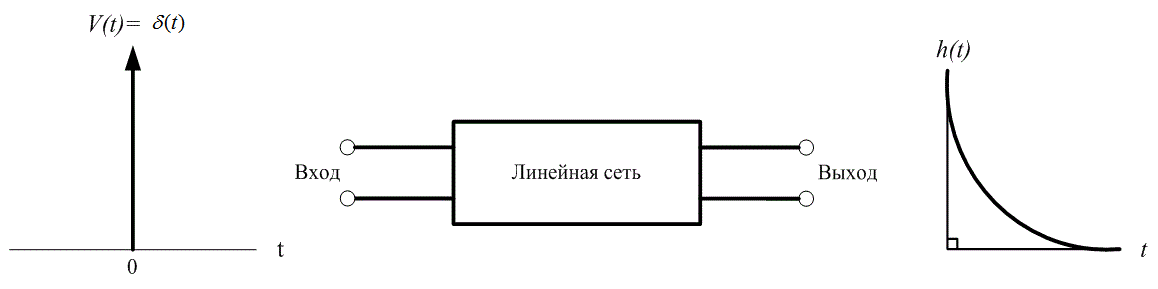
Рис. А.8. Импульсная характеристика линейной системы
Поскольку нас интересует как время подачи импульсов на вход, так и время наблюдения реакции на них на выходе, следует весьма аккуратно относиться к записи времени. Поэтому определим две различные временные последовательности; начнем с использования следующей формы записи.
1. Время на входе будем обозначать через ![]() , так что входные импульсы напряжения будут записываться как
, так что входные импульсы напряжения будут записываться как ![]() ,
, ![]() , …,
, …, ![]() .
.
2. Время на выходе будем обозначать через t, так что выходные функции тока будут записываться как i(t1), i(t2), …, i(tN).
Хевисайд нашел отклик схемы (или ток на выходе) для каждого входного импульса; после этого он сложил эти токи и получил общий ток на выходе. Весовой коэффициент прямоугольного импульса, поданного в момент ![]() — это произведение
— это произведение ![]() . Если устремить
. Если устремить ![]() к нулю, последовательность импульсов будет аппроксимировать произвольное входное напряжение настолько точно, насколько это нужно. Снова отметим, что момент подачи импульса на вход — это
к нулю, последовательность импульсов будет аппроксимировать произвольное входное напряжение настолько точно, насколько это нужно. Снова отметим, что момент подачи импульса на вход — это ![]() , а момент определения реакции системы - ti, где
, а момент определения реакции системы - ti, где ![]() - переменная входного времени, a t - переменная выходного времени, i = 1, ..., N.
- переменная входного времени, a t - переменная выходного времени, i = 1, ..., N.
б)
Рис. А.9. Аппроксимация произвольного входного сигнала:
а) входной сигнал; б) аппроксимация входного сигнала
На рис. А.10 показана выходная реакция i(t) = A1h(t-![]() ) на импульс с весовым коэффициентом
) на импульс с весовым коэффициентом ![]() . Поскольку входной импульс в момент
. Поскольку входной импульс в момент ![]() не является единичным, он умножается на весовой коэффициент — интенсивность (или площадь)
не является единичным, он умножается на весовой коэффициент — интенсивность (или площадь) ![]() . В некоторый момент времени t1 где
. В некоторый момент времени t1 где ![]() , выходная реакция на импульс
, выходная реакция на импульс ![]() , как показано на рис. А.10, выражается следующим образом.
, как показано на рис. А.10, выражается следующим образом.
![]() при
при ![]()
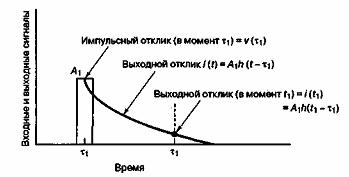
Рис. А. 10. Реакция на импульс в момент ![]()
При наличии нескольких входных импульсов общий выходной отклик линейной системы — это просто сумма отдельных откликов. На рис. А.11 показан отклик сети на два единичных импульса. При N импульсах на входе ток на выходе, измеренный в момент времени t1, можно записать следующим образом.
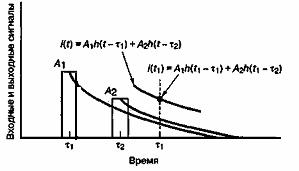
Рис. А. 11. Реакция на два импульса
i(t1) = ![]() +
+![]() + …+
+ …+![]() ,
,
где импульсы подаются в моменты ![]() ,
, ![]() , …,
, …, ![]() и где
и где ![]() .
.
Все импульсы, поданные на вход после момента t1, не учитываются, поскольку они не дают вклада в i(t1). Это согласуется с требованием причинности физически реализуемых систем — отклик системы должен быть нулевым до применения возмущения. Итак, можно записать ток на выходе в любой момент времени t следующим образом.
i(t) = ![]() +
+![]() + …+
+ …+![]()
или, поскольку весовой коэффициент импульса в момент времени ![]() равен
равен ![]() ,
,
![]() (A.43)
(A.43)
Когда ![]() стремится к нулю, сумма входных импульсов — к действительному напряжению
стремится к нулю, сумма входных импульсов — к действительному напряжению ![]() ,
, ![]() можно заменить
можно заменить ![]() , при этом сумма переходит в интеграл свертки.
, при этом сумма переходит в интеграл свертки.
![]() (А.44,а)
(А.44,а)
или
![]() (A.44,б)
(A.44,б)
В сокращенной записи
![]() (A.45)
(A.45)
Итак, i(t) - это сумма реакций на отдельные импульсные возмущения, произведенные в некоторый входной момент ![]() , причем каждый импульс умножается на весовой коэффициент — интенсивность.
, причем каждый импульс умножается на весовой коэффициент — интенсивность.
А.5.1. Графическая иллюстрация свертки
Рассмотрим квадратный импульс v(t), подаваемый на вход линейной сети, импульсная характеристика которой равна h(t) (рис. А. 12, а). Отклик на выходе описывается интегралом свертки, представленным в формуле (А.44).
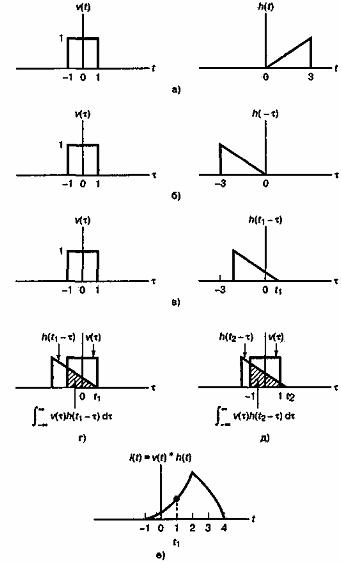
Рис. А. 12. Графическая иллюстрация свертки
Независимой переменной в интеграле свертки является ![]() . На рис. А. 12, б показаны функции
. На рис. А. 12, б показаны функции ![]() и
и ![]() . Отметим, что
. Отметим, что ![]() получается отображением
получается отображением ![]() относительно оси
относительно оси ![]() . Член
. Член ![]() представляет функцию
представляет функцию ![]() , смещенную на t секунд вдоль положительного направления оси
, смещенную на t секунд вдоль положительного направления оси ![]() . На рис. А. 12, в показана функция
. На рис. А. 12, в показана функция ![]() . Значение интеграла свертки в момент времени t=t1 получается из формулы (А.44), в которой положено t = tl. Это просто площадь под кривой произведения
. Значение интеграла свертки в момент времени t=t1 получается из формулы (А.44), в которой положено t = tl. Это просто площадь под кривой произведения ![]() на
на ![]() , показанного на рис. А. 12, г. Подобным образом интеграл свертки, взятый в момент t = t2, равен заштрихованной области на рис. А. 12, д. На рис. А. 12, е приведен график отклика на выходе схемы при квадратном импульсе на входе, показанном на рис. А. 12, а. Каждое вычисление интеграла свертки для некоторого момента времени t1 дает одну точку i(ti) графика на рис. А.12, е.
, показанного на рис. А. 12, г. Подобным образом интеграл свертки, взятый в момент t = t2, равен заштрихованной области на рис. А. 12, д. На рис. А. 12, е приведен график отклика на выходе схемы при квадратном импульсе на входе, показанном на рис. А. 12, а. Каждое вычисление интеграла свертки для некоторого момента времени t1 дает одну точку i(ti) графика на рис. А.12, е.
А.5.2. Свертка по времени
Если ![]() и
и ![]() , то
, то
![]()
![]()
Для линейных систем порядок интегрирования можно изменить.
![]() (A.46)
(A.46)
С помощью свойства сдвига во времени второе интегральное выражение правой части можно заменить на ![]() .
.
![]() (A.47)
(A.47)
Следовательно, операцию свертки во временной области можно заменить умножением в частотной области.
А.5.3. Свертка по частоте
Можно показать, что, вследствие симметрии пары преобразований Фурье (формулы (А.26) и (А.27)), умножение во временной области переходит в свертку в частотной области.
![]() (A.48)
(A.48)
Данный переход умножения в одной области в свертку в другой весьма удобен, поскольку, как правило, одну из этих операций выполнить значительно проще, чем другую. Например, ранее говорилось, что Хевисайд использовал свертку для нахождения тока на выходе линейной системы при подаче на вход произвольного переменного напряжения. Подобные методы часто включают вычисление (иногда трудоемкое) свертки входного сигнала с импульсной характеристикой системы. Поскольку, как видно из формулы (А.47), свертка во временной области переходит в умножение в частотной, для линейной системы входной сигнал можно просто умножить на передаточную функцию системы. Выходной сигнал затем получается путем применения к произведению обратного преобразования Фурье.
![]() (А.49)
(А.49)
Вычислить выражение (А.49) часто намного проще, чем (А.45). В то же время, при определенных обстоятельствах, операция свертки настолько проста, что ее можно выполнить графически, просто внимательно изучив соответствующий график. Предположим, что некоторый произвольный сигнал необходимо умножить на косинусоиду фиксированной частоты, например несущую (если речь идет о модуляции). С помощью формулы (А.48) спектр произвольного сигнала можно свернуть со спектром косинусоиды, что, как показывается в следующем разделе, выполняется довольно просто.
А.5.4. Свертка функций с единичным импульсом
При использовании свойства, представленного в формуле (А.47), очевидно, что если
![]()
и
![]() ,
,
то
![]() . (А.50)
. (А.50)
Также должно быть очевидно, что
![]() (A.51)
(A.51)
и
![]() (A.52)
(A.52)
Следовательно, можно сделать вывод, что свертка функции с единичным импульсом дает исходную функцию. Простое развитие формулы (А.52) дает следующее.
![]() (A.53)
(A.53)
На рис. А. 13 показано, насколько просто производится свертка спектра произвольного сигнала со спектром косинусоиды. На рис. А. 13, а представлен спектр X(f) произвольного узкополосного сигнала. На рис. А.13, б показан спектр ![]() . Выход Z(f) = Х(f)*Y(f) на рис. А.13, в получается при свертке спектра сигнала с импульсной функцией Y(f), согласно формуле (А.53), где импульсы действуют как стробирующие функции. Следовательно, в данном простом примере свертку можно выполнить графически, заметая стробирующие импульсы через спектр сигнала. Умножение на импульсные функции на каждом шаге заметания приводит к повторению спектра сигнала. Результат, показанный на рис. А.13, в, — это версия исходного спектра X(f), смещенная к месторасположению импульсных функций, изображенных на рис. А.13, б.
. Выход Z(f) = Х(f)*Y(f) на рис. А.13, в получается при свертке спектра сигнала с импульсной функцией Y(f), согласно формуле (А.53), где импульсы действуют как стробирующие функции. Следовательно, в данном простом примере свертку можно выполнить графически, заметая стробирующие импульсы через спектр сигнала. Умножение на импульсные функции на каждом шаге заметания приводит к повторению спектра сигнала. Результат, показанный на рис. А.13, в, — это версия исходного спектра X(f), смещенная к месторасположению импульсных функций, изображенных на рис. А.13, б.
А.5.5. Применение свертки при демодуляции
В разделе А.5.4 рассматривался сигнал, умноженный на ![]() . Было показано, как в частотной области выглядит свертка спектра сигнала со спектром косинусоиды. В данном разделе рассматривается обратный процесс. Необходимо демодулировать сигнал, умноженный на
. Было показано, как в частотной области выглядит свертка спектра сигнала со спектром косинусоиды. В данном разделе рассматривается обратный процесс. Необходимо демодулировать сигнал, умноженный на ![]() (сигнал нужно восстановить в его изначальном диапазоне частот).
(сигнал нужно восстановить в его изначальном диапазоне частот).
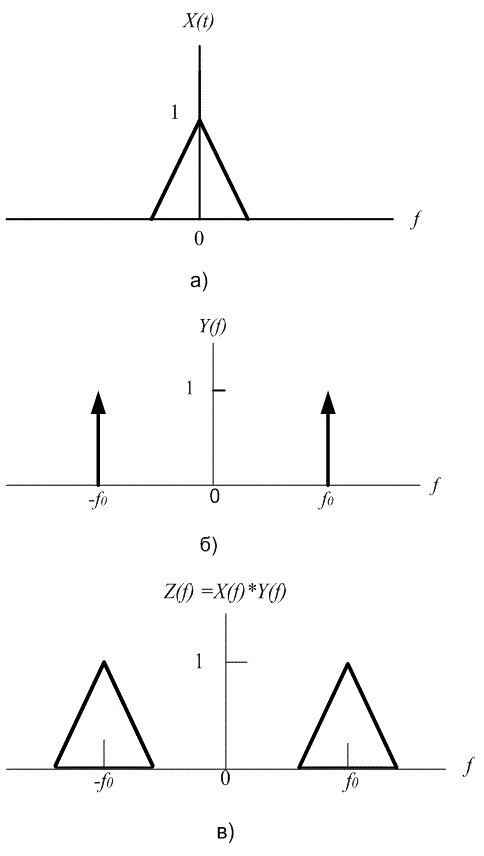
Рис. А.13. Свертка спектра сигнала со спектром косинусоиды
На рис. А. 14, а представлен спектр, Z(f), сигнала, смещенного вверх по частоте.
Можно демодулировать данный смещенный сигнал и восстановить исходный сигнал, умножив данный сигнал на ![]() . Вместо этого мы можем проиллюстрировать процесс обнаружения в частотной области, свернув Z(f) со спектром несущей,
. Вместо этого мы можем проиллюстрировать процесс обнаружения в частотной области, свернув Z(f) со спектром несущей, ![]() , показанным на рис. А. 14, б.
, показанным на рис. А. 14, б.
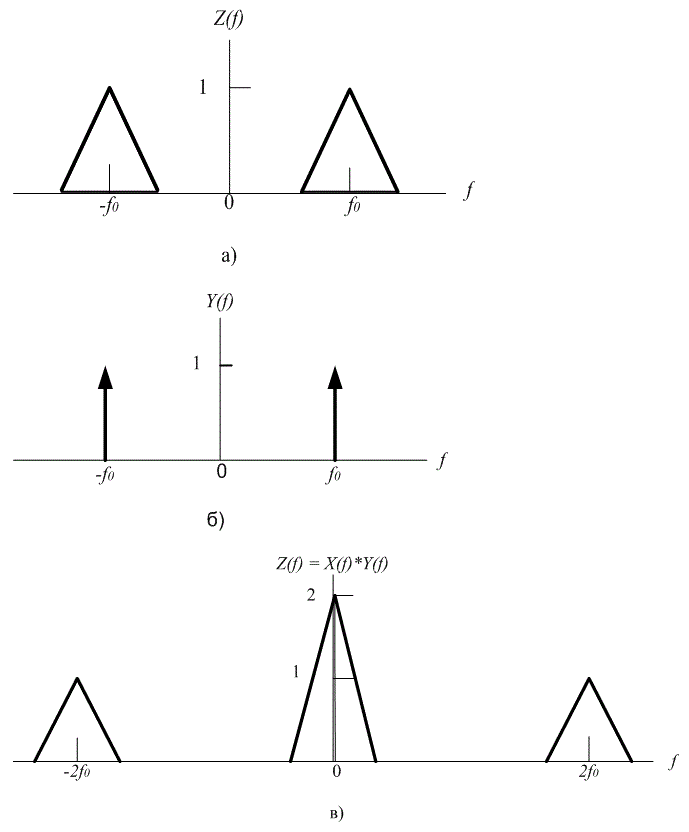
Рис. А.14. Применение демодуляции
Использование формул (А.52) и (А.53) позволяет записать следующее.
![]() (A.54)
(A.54)
Следовательно, результат демодуляции X(f)=Z(f)*Y(f) получаем в результате применения формулы (А. 54). Получающийся спектр сигнала — это спектр исходного сигнала плюс компоненты, центрированные на частотах ±2f0, как показано на рис. А. 14, в. Как и в предыдущем разделе, свертку можно выполнить графически. На рис. А. 14, в отображены следующие члены.
![]() =
=
= ![]()
+![]() =
=
= ![]() (А.55)
(А.55)
Отметим, что результат — это спектр исходного сигнала плюс члены, связанные с высокочастотными компонентами. Данный результат типичен для процесса обнаружения; высокочастотные члены отфильтровываются и отбрасываются, оставляя спектр демодулированного исходного сигнала.
А.6. Таблицы Фурье-образов и свойств преобразования Фурье
В табл. А.1 и А.2 приведены Фурье-образы наиболее часто встречающихся функций и некоторые свойства преобразования Фурье.
Таблица А. 1. Фурье-образы
|
|
|
|
1. |
1 |
|
2. 1 |
|
|
3. |
|
|
4. |
|
|
5. |
|
|
6. |
|
|
7. |
|
|
8. |
|
|
9. |
|
|
10. |
|
|
11. |
|
|
12. |
|
|
13. |
|
|
14. |
|
|
15. |
|
|
16. |
|
Примечание: rect(f/2W) = 1 для -W<f< W и 0 для | f | > W; sinc x = (sin![]() )/
)/![]() .
.
Таблица A. 2. Свойства преобразования Фурье
|
Действие |
|
|
|
1. Изменение масштаба |
x(at) |
|
|
2. Сдвиг во времени |
|
|
|
3. Сдвиг по частоте |
|
|
|
4. Дифференцирование по времени |
|
|
|
5. Дифференцирование по частоте |
|
|
|
6. Интегрирование по времени |
|
|
|
7. Свертка по времени |
|
|
|
8. Свертка по частоте |
|
|
Литература
1. Papoulis A. Signal Analysis. McGraw-Hill Book Company, New York, 1977.
2. Panter P. F. Modulation, Noise, and Spectral Analysis. McGraw-Hill Book Company, New York, 1965.
3. Bracewell R. The Fourier Transfer and Its Applications. McGraw-Hill Book Company, New York, 1978.
4. Haykin S. Communications Systems. John Wiley & Sons, Inc., New York, 1983.
5. Schwartz M. Information, Transmission, Modulation, and Noise. McGraw-Hill Book Company, New York, 1980.