Во многих радиотехнических задачах возникает необходимость учета случайного характера огибающих и начальных фаз узкополосных случайных процессов. При этом в качестве узкополосного процесса чаще всего выступает нормальный случайный процесс. Поэтому в дальнейшем мы остановимся на изучении такого вида процессов.

Итак, пусть – узкополосный случайный процесс, мгновенные значения которого распределены по нормальному закону с нулевым математическим ожиданием

.

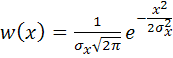Этому процессу соответствует комплексный случайный процесс

,

причем комплексно-сопряженный процесс также распределен по нормальному закону с нулевым математическим ожиданием и той же дисперсией, т.е.

.

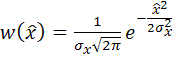Так как значения и некоррелированы, а для нормальных случайных процессов некоррелированность означает и статистическую независимость, то это значит, что двумерная плотность вероятности

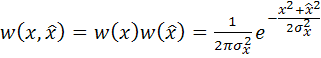. (5.95)

Для определения законов распределения огибающей и начальной фазы необходимо перейти от декартовой к полярной системе координат (рис. 5.10) связь между двумя координатными 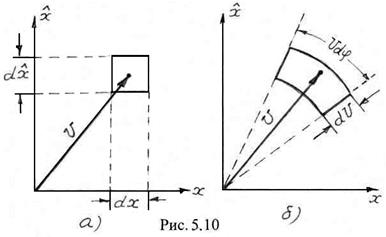системами определяется следующими соотношениями:

; . (5.96)

Выделим бесконечно малую область в окрестности конца вектора в декартовой системе координат (рис. 5.10а). Очевидно, площадь этой области будет равна , а вероятность попадания конца вектора в эту область

. (5.97)

При переходе к полярной системе координат область трансформируется в область (рис. 5.10б). Вероятность попадания конца вектора в эту область будет равна:

. (5.98)

Так как при переходе из одной системы координат в другую вероятности попадания конца вектора в элементарные области должны

быть равны, приравняем правые части (5.97) и (5.98)

. (5.99)

Подстановка (5.95) и (5.96) в (5.99) с учетом того, что ; после несложных преобразований дает

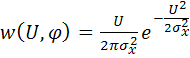. (5.100)

Выражение (5.100) представляет собой двумерную плотность распределения значений огибающей и начальной фазы узкополосного СП.

Для того, чтобы найти одномерную плотность распределения огибающей необходимо (5.100) проинтегрировать по всем значениям фазы от до

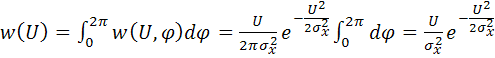. (5.101)

Таким образом, значения огибающей узкополосного СП распределены по закону Рэлея.

Аналогично для определения одномерной плотности распределения значений начальной фазы проинтегрируем (5.100) по всем значениям от до

.

Подстановка в это выражение формулы (5.100) с учетом того, что

,

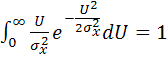(условие нормировки), дает:

. (5.102)

Отсюда следует, что значения фазы узкополосного СП распределены по равномерному закону в пределах от до .

Рассмотри случай, когда случайный процесс представляет сумму узкополосного детерминированного сигнала

,

и случайного процесса (5.84). Представляя суммарный процесс в комплексной форме и проводя аналогичные рассуждения, можно получить выражение для одномерной плотности вероятности огибающей

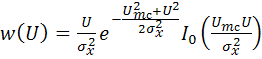, (5.103)

где – модифицированная функция Бесселя нулевого порядка.

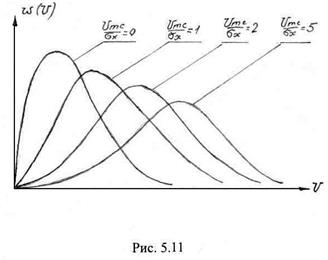Выражение (5.103) представляет собой обобщенный закон Рэлея или закон Райса. На рис. 5.11 представлены кривые плотности вероятности огибающей суммарного процесса. Из рисунка следует, что форма кривой и ее положение зависит от отношения , т.е. от отношения амплитуды сигнала к средне-квадратичному значению шума, в качестве которого здесь выступает процесс (5.84). При кривая закона Райса приближается к нормальному закону.