2.8.1. Представление двоичных цифр в форме сигналов
2.8.3. Спектральные параметры сигналов PCM
2.8.4. Число бит на слово PCM и число бит на символ
2.8.1. Представление двоичных цифр в форме сигналов
В разделе 2.6 показывалось, как аналоговые сигналы преобразовываются в двоичные цифры посредством использования РСМ. В результате этого не получается ничего «физического», только цифры. Цифры - это просто абстракция, способ описания информации, содержащейся в сообщении. Следовательно, нам необходимо иметь что-то физическое, что будет представлять цифры или «являться носителем» цифр.
Чтобы передать двоичные цифры по узкополосному каналу, будем представлять их электрическими импульсами. Подобное представление изображено на рис. 2.21. На рис. 2.21, а показаны разделенные во времени интервалы передачи кодовых слов, причем каждое кодовое слово является 4-битовым представлением квантованной выборки. На рис. 2.21, б каждая двоичная единица представляется импульсом, а каждый двоичный нуль - отсутствием импульса. Таким образом, последовательность электрических импульсов, представленная на рис. 2.21, б, может использоваться для передачи информации двоичного потока РСМ, а значит информации, закодированной в квантованных выборках сообщения.
Задача приемника - определить в каждый момент приема бита, имеется ли импульс в канале передачи. В разделе 2.9 будет показано, что вероятность точного определения наличия импульса является функцией энергии принятого импульса (или площади под графиком импульса). Следовательно, ширину импульса 
(рис. 2.21, б) выгодно делать как можно больше. Если увеличить ширину импульса до максимально возможного значения (равного времени передачи бита 
), то получится сигнал, показанный на рис. 2.21, в. Вместо того чтобы описывать этот сигнал как последовательность импульсов и их отсутствий (униполярное представление), мы можем описать его как последовательность переходов между двумя ненулевыми уровнями (биполярное представление). Если сигнал находится на верхнем уровне напряжения, он представляет двоичную единицу, а если на нижнем - двоичный нуль.
2.8.2. Типы сигналов РСМ
При применении импульсной модуляции к двоичному символу получаем двоичный сигнал, называемый сигналом с импулъсно-кодовой модуляцией (pulse-code modulation - PCM). Существует несколько типов сигналов РСМ; они изображены на рис. 2.22 и будут описаны ниже. В приложениях телефонной связи эти сигналы часто именуются кодами канала (line code).
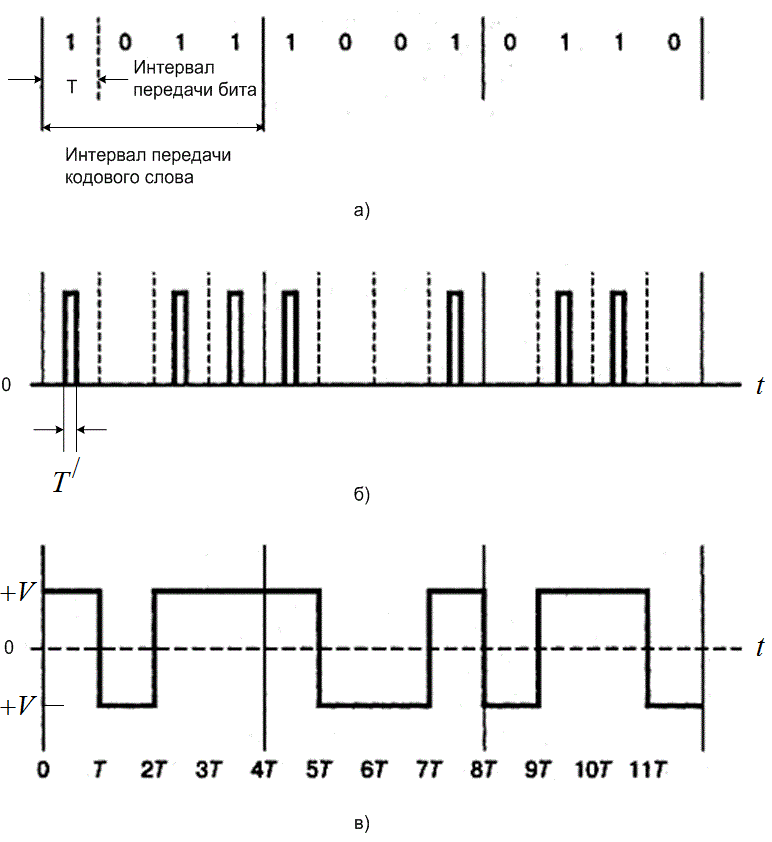
Рис. 2.21. Пример представления двоичных цифр в форме сигналов:
а) последовательность PCM; б) импульсное представление последовательности PCM; в) импульсный сигнал (переход между двумя уровнями)
При применении импульсной модуляции к недвоичному символу получаем сигнал, называемый М-арным импульсно-модулированным; существует несколько типов таких сигналов. Описываются они в разделе 2.8.5, особое внимание уделяется амплитудно-импульсной модуляции (pulse-amplitude modulation - РАМ). На рис. 2.1 в выделенном блоке «Узкополосная передача сигналов» показана базовая классификация сигналов РСМ и М-арных импульсных сигналов. Сигналы РСМ делятся на четыре группы.
1. Без возврата к нулю (nonreturn-to-zero - NRZ)
2. С возвратом к нулю (return-to-zero - RZ)
3. Фазовое кодирование
4. Многоуровневое бинарное кодирование
Самыми используемыми сигналами РСМ являются, пожалуй, сигналы в кодировках NRZ. Группа кодировок NRZ включает следующие подгруппы: NRZ-L (L = level - уровень), NRZ-M (М = mark - метка) и NRZ-S (S = space - пауза). Кодировка NRZ-L (nonreturn-to-zero level - без возврата к нулевому уровню) широко используется в цифровых логических схемах. Двоичная единица в этом случае представляется одним уровнем напряжения, а двоичный нуль - другим.
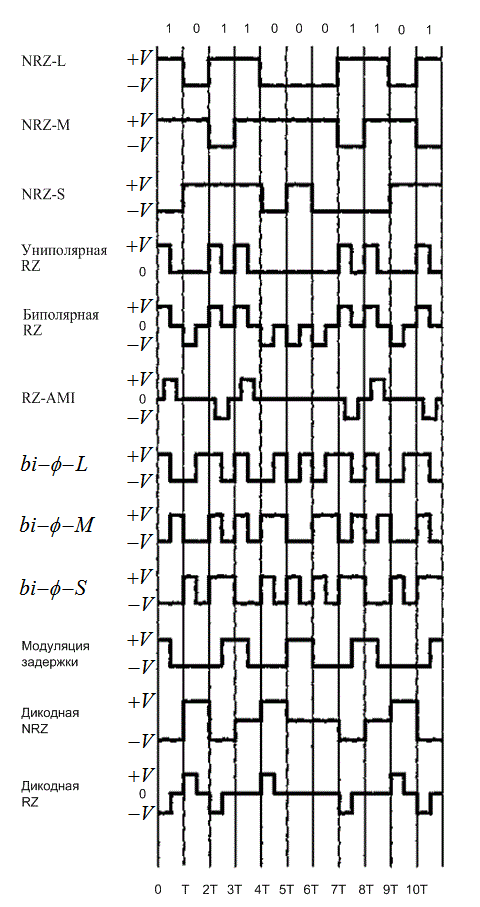
Рис.2.22. Различные сигналы PCM
Изменение уровня происходит всякий раз при переходе в последовательности передаваемых битов от нуля к единице или от единицы к нулю. При использовании кодировки NRZ-M двоичная единица, или метка (mark), представляется изменением уровня, а нуль, или пауза (space), - отсутствием изменения уровня. Такая кодировка часто называется дифференциальной. Применяется кодировка NRZ-M преимущественно при записи на магнитную ленту. Кодировка NRZ-S является обратной к кодировке NRZ-M: двоичная единица представляется отсутствием изменения уровня, а двоичный нуль - изменением уровня.
Группа кодировок RZ включает униполярную кодировку RZ, биполярную кодировку RZ и кодировку RZ-AMI. Эти коды применяются при узкополосной передаче данных и магнитной записи. В униполярной кодировке RZ единица представляется наличием импульса, длительность которого составляет половину ширины бита, а нуль - его отсутствием. В биполярной кодировке RZ единицы и нули представляются импульсами противоположных уровней, длительность каждого из которых также составляет половину ширины бита. В каждом интервале передачи бита присутствует импульс. Кодировка RZ-AMI (AMI = alternate mark inversion - с чередованием полярности) - это схема передачи сигналов, используемая в телефонных системах. Единицы представляются наличием импульсов равных амплитуд с чередующимися полярностями, а нули - отсутствием импульсов.
Группа фазового кодирования включает следующие кодировки: 
(bi-phase-level - двухфазный уровень), более известная как манчестерское кодирование (Manchester encoding); 
(bi-phase-mark); 
(bi-phase-space); и модуляция задержки (delay modulation - DM), или кодировка Миллера. Схемы фазовых кодировок используются в системах магнитной записи и оптической связи, а также в некоторых спутниковых телеметрических каналах передачи данных. В кодировке единица представляется импульсом, длительностью в половину ширины бита, расположенным в первой половине интервала передачи бита, а нуль - таким же импульсом, но расположенным во второй половине интервала передачи бита. В кодировке в начале каждого интервала передачи бита происходит переход. Единица представляется вторым переходом в середине интервала, нуль - единственным переходом в начале интервала передачи бита. В кодировке в начале каждого интервала также происходит переход. Единица представляется этим единственным переходом, а для представления нуля необходим второй переход в середине интервала. При модуляции задержки [4] единица представляется переходом в середине интервала передачи бита, а нуль - отсутствием иных переходов, если за ним не следует другой нуль. В последнем случае переход помещается в конец интервала передачи первого нуля. Приведенные объяснения станут понятнее, если обратиться к рис. 2.22.
Многие двоичные сигналы для кодировки двоичных данных используют три уровня, а не два. К этой группе относятся сигналы в кодировках RZ и RZ-AMI. Кроме того, сюда входят схемы, называемые дикодной (dicode) и двубинарной кодировкой (duobinary). При дикодной кодировке NRZ переходы в передаваемой информации от единицы к нулю и от нуля к единице меняют полярность импульсов; при отсутствии переходов передается сигнал нулевого уровня. При дикодной кодировке RZ переходы от единицы к нулю и от нуля к единице вызывают изменение полярности, длительностью в половину интервала импульса; при отсутствии переходов передается сигнал нулевого уровня. Подробнее трехуровневые двубинарные схемы передачи сигналов рассмотрены в разделе 2.9.
Может возникнуть вопрос, почему так много различных сигналов РСМ? Неужели так много уникальных приложений требуют разнообразных кодировок для представления двоичных цифр? Причина такого разнообразия заключается в отличии производительности, которая характеризует каждую кодировку [5]. При выборе кодировки РСМ внимание следует обращать на следующие параметры.
1. Постоянная составляющая. Удаление из спектра мощностей постоянной составляющей позволяет системе работать на переменном токе. Системы магнитной записи или системы, использующие трансформаторную связь, слабо чувствительны к гармоникам очень низких частот. Следовательно, существует вероятность потери низкочастотной информации.
2. Автосинхронизация. Каждой системе цифровой связи требуется символьная или битовая синхронизация. Некоторые кодировки РСМ имеют встроенные функции синхронизации, помогающие восстанавливать синхронизирующий сигнал. На пример, манчестерская кодировка включает переходы в середине каждого интервала передачи бита, вне зависимости от передаваемого знака. Этот гарантированный переход и может использоваться в качестве синхронизирующего сигнала.
3. Выявление ошибок. Некоторые схемы, такие как двубинарная кодировка, предлагают средство выявления информационных ошибок без введения в последовательность данных дополнительных битов выявления ошибок.
4. Сжатие полосы. Такие схемы, как, например, многоуровневые кодировки, повышают эффективность использования полосы, разрешая уменьшение полосы, требуемой для получения заданной скорости передачи данных; следовательно, на единицу полосы приходится больший объем передаваемой информации.
5. Дифференциальное кодирование. Этот метод позволяет инвертировать полярность сигналов в дифференциальной кодировке, не затрагивая при этом процесс обнаружения данных. Это большой плюс в системах связи, в которых иногда происходит инвертирование сигналов. (Дифференциальная кодировка подробно рассмотрена в главе 4, раздел 4.5.2.)
6. Помехоустойчивость. Различные типы сигналов РСМ могут различаться по вероятности появления ошибочных битов при данном отношении сигнал/шум. Некоторые схемы более устойчивы к шумам, чем другие. Например, сигналы в кодировке NRZ имеют лучшую достоверность передачи, чем сигналы в униполярной кодировке RZ.
2.8.3. Спектральные параметры сигналов РСМ
Наиболее распространенными критериями, используемыми при сравнении кодировок РСМ и выборе подходящего типа сигнала из многих доступных, являются спектральные характеристики, возможности битовой синхронизации и выявления ошибок, устойчивость к интерференции и помехам, а также цена и сложность реализации. Спектральные характеристики некоторых распространенных кодировок РСМ показаны на рис. 2.23. Здесь изображена зависимость спектральной плотности мощности (измеряется в Вт/Гц) от нормированной ширины полосы, WT, где W- ширина полосы, а Т- длительность импульса. Произведение WT часто называют базой сигнала. Поскольку скорость передачи импульсов или сигналов 
обратна Т, нормированную ширину полосы можно также выразить как 
. Из последнего выражения видно, что нормированная ширина полосы измеряется в герц/(импульс/с) или в герц/(символ/с). Это относительная мера ширины полосы; она описывает, насколько эффективно используется полоса пропускания при интересующей нас кодировке. Считается, что любой тип кодировки, требующий менее 1,0 Гц для передачи одного символа в секунду, эффективно использует полосу. Примеры: модулирование задержки и двубинарная кодировка (см. раздел 2.9). Для сравнения, любая кодировка, требующая более 1,0 Гц полосы для передачи одного символа в секунду, неэффективно использует полосу. Пример: двухфазная (манчестерская) кодировка. На рис. 2.23 можно также видеть распределение энергии сигналов в различных кодировках по спектру. Например, двубинарная кодировка и схема NRZ имеют значительное число спектральных компонентов около постоянной составляющей и на низких частотах, тогда как двухфазная кодировка вообще не содержит энергии на частоте постоянной составляющей.
Важным параметром измерения эффективности использования полосы является отношение R/W (измеряется в бит/с/герц). Эта мера характеризует скорость передачи данных, а не скорость передачи сигналов. Для данной схемы передачи сигналов отношение R/W описывает, какой объем данных может быть передан из расчета на каждый герц доступной полосы. (Подробнее об эффективности использования полосы в главе 9.)
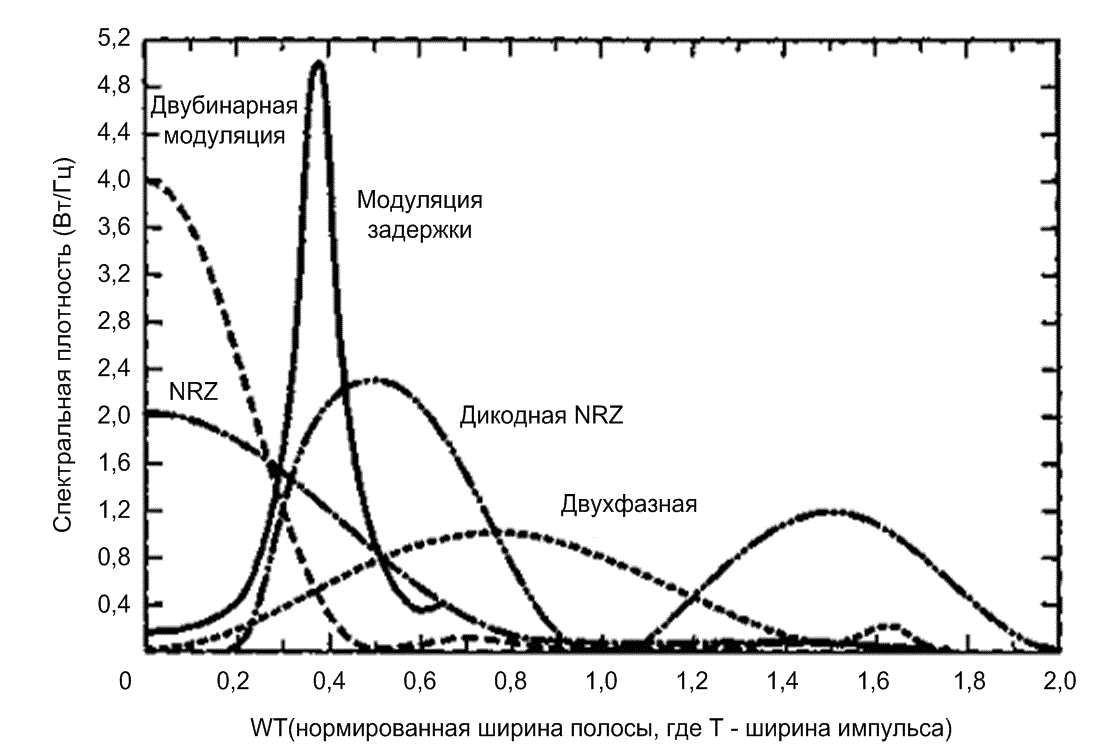
Рис.2.23. Спектральные плотности различных кодировок PCM
2.8.4. Число бит на слово РСМ и число бит на символ
До настоящего момента для разбиения битов на группы с целью формирования символов для обработки и передачи сигналов использовалось двоичное разделение 
. Рассмотрим теперь аналогичное приложение, где также применима концепция 
. Опишем процесс форматирования аналоговой информации в двоичный поток посредством дискретизации, квантования и кодирования. Каждая аналоговая выборка преобразовывается в слово РСМ, состоящее из группы битов. Размер слова РСМ можно выразить через число квантовых уровней, разрешенных для каждой выборки; это равно числу значений, которое может принимать слово РСМ. Квантование также можно описать числом битов, требуемых для определения этого набора уровней. Связь между числом уровней на выборку и количеством битов, необходимых для представления этих уровней, аналогична связи между размером набора символов сообщения и числом битов, необходимых для представления символа . Чтобы различать эти два случая, изменим форму записи для сигналов РСМ. Вместо будем писать 
, где L - число квантовых уровней в слове РСМ, а l - число битов, необходимых для представления этих уровней.
2.8.4.1. Размер слова РСМ
Сколько бит нужно выделить каждой аналоговой выборке? Для цифровых телефонных каналов каждая выборка речевого сигнала кодируется с использованием 8 бит, что дает 
, или 256 уровней на выборку. Выбор числа уровней (или числа бит на выборку) зависит от того, какое искажение, вызванное квантованием, мы можем допустить при использовании формата РСМ. Вообще, полезно вывести общую формулу, выражающую соотношение между требуемым числом бит на аналоговую выборку (размер слова РСМ) и допустимым искажением, вызванным квантованием. Итак, пусть величина ошибки вследствие квантования, |e|, определяется как часть р удвоенной амплитуды напряжения аналогового сигнала.
(2.24)
Поскольку ошибка квантования не может быть больше 
, где q - интервал квантования, можем записать
, (2.25)
где L - число уровней квантования. Для большинства приложений число уровней достаточно велико, так что (L-1) можно заменить L, что и было сделано выше. Следовательно, из формул (2.24) и (2.25) можем записать следующее.
(2.26)
уровней (2.27)
и
бит (2.28)
Важно отметить, что мы не путаем число бит на слово РСМ, обозначенное через l в уравнении (2.28), и число бит k, используемое в описании M-уровневой передачи данных. (Несколько ниже приводится пример 2.3, который поможет понять, чем отличаются эти два понятия.)
2.8.5. M-арные импульсно-модулированные сигналы
Существует три основных способа модулирования информации в последовательность импульсов: можно варьировать амплитуду, положение или длительность импульсов, что дает, соответственно, следующие схемы: амплитудно-импульсная модуляция (pulse-amplitude modulation - РАМ), фазово-импульсная модуляция (pulse-position modulation - PPM) и широтно-импульсная модуляция (pulse-duration modulation - PDM или pulse-width modulation - PWM). Если информационные выборки без квантования модулируются в импульсы, получаемая импульсная модуляция называется аналоговой. Если информационные выборки вначале квантуются, превращаясь в символы М-арного алфавита, а затем модулируются импульсами, получаемая импульсная модуляция является цифровой, и мы будем называть ее М-арной импульсной модуляцией. При М-арной амплитудно-импульсной модуляции каждому из М возможных значений символов присваивается один из разрешенных уровней амплитуды. Ранее сигналы РСМ описывались как двоичные, имеющие два значения амплитуды (например, кодировки NRZ, RZ). Отметим, что такие сигналы РСМ, требующие всего двух уровней, представляют собой частный случай (М=2) М-арной кодировки РАМ. В данной книге сигналы РСМ выделены (см. разделы 2.1 и 2.8.2) и рассмотрены особо, поскольку они являются наиболее популярными схемами импульсной модуляции.
М-арная фазово-импульсная модуляция (РРМ) сигнала осуществляется через задержку (или упреждение) появления импульса на время, соответствующее значению информационных символов. M-арная широтно-импульсная модуляция (PDM) осуществляется посредством измерения ширины импульса на величину, соответствующую значению символа. Для кодировок РРМ и PDM амплитуда импульса фиксируется. Стоит отметить, что узкополосные модуляции с использованием импульсов имеют аналоги среди полосовых модуляций. Кодировка РАМ подобна амплитудной модуляции, тогда как кодировки РРМ и PDM подобны, соответственно, фазовой и частотной модуляциям. В данном разделе мы рассмотрим только M-арные сигналы РАМ и сопоставим их с сигналами РСМ.
Полоса пропускания, необходимая для двоичных цифровых сигналов, таких как сигналы в кодировке РСМ, может быть очень большой. Как сузить требуемую полосу? Одна из возможностей - использовать многоуровневую передачу сигналов. Рассмотрим двоичный поток со скоростью передачи данных R бит/секунду. Чтобы не передавать импульсные сигналы для каждого отдельного бита, можно вначале разделить данные на k-битовые группы, после чего использовать для передачи -уровневые импульсы. При такой многоуровневой передаче сигналов, или M-арной амплитудно-импульсной модуляции, каждый импульсный сигнал может теперь представлять M-битовый символ в потоке символов, перемещающемся со скоростью R/k символов в секунду (в k раз медленнее, чем поток битов). Следовательно, при данной скорости передачи данных для уменьшения числа символов, передаваемых в секунду, может использоваться многоуровневая (М>2) передача сигналов; другими словами, при уменьшении требований к ширине полосы передачи может применяться не двоичная кодировка РСМ, а М-уровневая кодировка РАМ. Чем мы платим за такое сужение полосы, и платим ли мы вообще чем-либо? Разумеется, ничто не достается даром, и это будет рассмотрено ниже.
Рассмотрим задачу, которую должен выполнять приемник. Он должен различать все возможные уровни каждого импульса. Одинаково ли легко приемник различает восемь возможных уровней импульса, приведенного на рис. 2.24, а, и два возможных уровня каждого двоичного импульса на рис. 2.24, б? Передача восьмиуровневого (по сравнению с двухуровневым) импульса требует большей энергии для эквивалентной эффективности обнаружения. (Достоверность обнаружения сигнала определяется отношением 
в приемнике.) При равной средней мощности двоичных и восьмеричных импульсов первые обнаружить проще, поскольку детектор приемника при принятии решения о принадлежности сигнала к одному из двух уровней располагает большей энергией сигнала на каждый уровень, чем при принятии решения относительно принадлежности сигнала к одному из 8 уровней. Чем расплачивается разработчик системы, если решает использовать более удобную в обнаружении двоичную кодировку РСМ, а не восьмиуровневую кодировку РАМ? Плата состоит в трехкратном увеличении ширины полосы для данной скорости передачи данных, по сравнению с восьмеричными импульсами, поскольку каждый восьмеричный импульс должен заменяться тремя двоичными (ширина каждого из которых втрое меньше ширины восьмеричного импульса). Может возникнуть вопрос, почему бы ни использовать двоичные импульсы той же длительности, что и восьмеричные, и разрешить запаздывание информации? В некоторых случаях это приемлемо, но для систем связи реального времени такое увеличение задержки допустить нельзя - шестичасовые новости должны приниматься в 6 часов. (В главе 9 будет подробно рассмотрен компромисс между мощностью сигнала и шириной полосы передачи.)
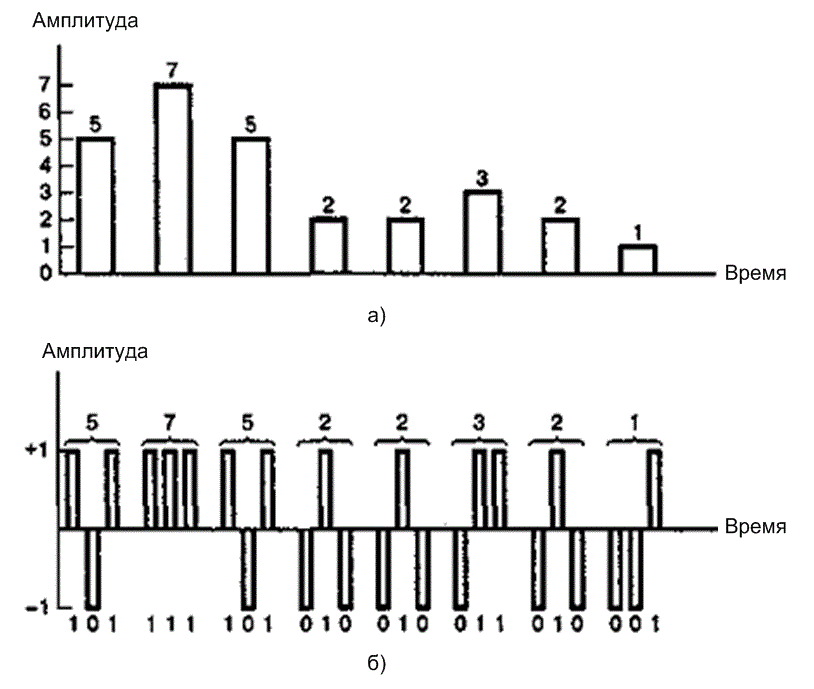
Рис.2.24. Передача сигналов с использованием импульсно-кодовой модуляции: а) восьмиуровневая передача; б) двухуровневая передача
Пример 2.3. Уровни квантования и многоуровневая передача сигналов
Информацию в форме аналоговых сигналов с максимальной частотой 
кГц необходимо передать через систему с M-уровневой кодировкой РАМ, где общее число уровней импульсов М=16. Искажение, вызванное квантованием, не должно превышать 
удвоенной амплитуды аналогового сигнала.
а) Чему равно минимальное число бит в выборке или слове РСМ, которое можно использовать при оцифровывании аналогового сигнала?
б) Чему равны минимальная требуемая частота дискретизации и получаемая при этом скорость передачи битов?
в) Чему равна скорость передачи импульсов в кодировке РАМ (или символов)?
г) Если ширина полосы передачи (включая фильтрацию) равна 12 кГц, чему будет равно эффективное использование полосы для этой системы?
В этом примере мы имеем дело с двумя типами уровней: несколькими уровнями квантования, необходимыми для удовлетворения требовании ограничения искажения, и 16 уровнями импульсов в кодировке РАМ.
Решение
а) С помощью формулы (2.28) вычисляем следующее.
Следовательно, l=6 уровней удовлетворяют требованиям, относящимся к искажению.
б) Используя критерий Найквиста, получаем минимальную частоту дискретизации 
выборок/секунду. Из п. а получаем, что каждая выборка - это 6-битовое слово в кодировке РСМ. Следовательно, скорость передачи битов 
бит/с.
в) Поскольку нужно использовать многоуровневые импульсы с 
уровнями, то 
бит/символ. Следовательно, поток битов разбивается на группы по 4 бита с целью формирования новых 16-уровневых цифр РАМ, и полученная скорость передачи символов равна 
символов/с.
г) Эффективность использования полосы - это отношение пропускной способности к ширине полосы в герцах, R/W. Поскольку R=36000 бит/с, a W=12 кГц, получаем R/W=3 бит/с/Гц.