1. Информационные характеристики сигнала

2. Энтропия дискретного источника с независимым выбором сообщений

3. Энтропия дискретного источника с зависимыми сообщениями

4. Избыточность источника

5. Производительность источника

6. Совместная энтропия двух источников

7. Взаимная информация источников сообщений

8. Скорость передачи и пропускная способность канал связи

9. Статистическое кодирование дискретных сообщений

10. Энтропия непрерывного источника и её свойства

11. Пропускная способность непрерывного канала связи

12. Эпсилон-энтропия источника непрерывных сообщений

1. Информационные характеристики сигнала

Система связи служит для передачи сообщений от производителя к получателю. Однако не всякое сообщение содержит информацию. Информация – это совокупность сведений об объекте или явлении, которые увеличивают знания потребителя об этом объекте или явлении.

В математической теории связи(теории информации) исходят из того, что в некотором сообщении x_i количество информации I(x_i) зависит не от её конкретного содержания, степени важности и т.д., а от того, каким образом выбирается данное сообщение из общей совокупности возможных сообщений.

В реальных условиях выбор конкретного сообщения производится с некоторой априорной вероятностью P(x_i). Чем меньше эта вероятность, тем больше информации содержится в данном сообщении.

Вероятностный подход и положен в основу определения меры количества информации.

При определении количества информации исходят из следующих требований:

1. Количественная мера информации должна обладать свойством аддитивности: количество информации в нескольких независимых сообщениях должно равняться сумме количества информации в каждом сообщении.

2. Количество информации о достоверном событии (P(x_i)=1) должно равняться нулю, так как такое сообщение не увеличивает наших знаний о данном объекте или явлении.

Указанным требованиям удовлетворяет логарифмическая мера, определяемая формулой

(1)

Чаще всего логарифм берётся с основанием 2, реже – с основанием e:

двоичных систем информации(бит)

натуральных единиц информации(нит)

Одну единицу информации содержит сообщение, вероятность выбора которого равняется 1/2.

В этом случае

двоичных единиц информации (бит)

При применении натуральных логарифмов одну натуральную единицу информации содержит сообщение, вероятность выбора которого равняется 1/e: натуральных единиц информации (нит)

Учитывая, что в практике передачи и преобразования информации широко применяются двоичные символы, двоичная логика, двоичные источники сообщений и двоичные каналы передачи, наиболее часто используется двоичная единица информации (бит).

Хотя при определении количества информации под сообщениями модно понимать любые фразы или телеграфные сообщения, мы здесь элементарными сообщениями будем называть отдельные буквы или слова. При использовании двухуровневых дискретных сигналов, например, мы будем пользоваться элементарными двоичными сигналами “0” и “1” считая их буквами.

Таким образом, алфавит двоичного источника состоит всего из двух букв, из которых можно строить длинные комбинации, называемые кодовыми словами.

2. Энтропия дискретного источника с независимым выбором сообщений

В теории информации чаще всего необходимо знать не количество информации I(x_i) содержащееся в отдельном сообщении, а среднее количество информации в одном сообщении, создаваемом источником сообщений.

Если имеется ансамбль(полная группа) из k сообщений x₁, x₂,… x_i,..x_k с вероятностями P(x₁)…P(x_k), то среднее количество информации, приходящееся на одно сообщение и называемое энтропией источника сообщений H(x) определяется формулой

(2) или

(3)

Размерность энтропии – количество единиц информации на символ. Энтропия характеризует источник сообщений с точки зрения неопределённости выбора того или другого сообщения.

Рассмотрим свойства энтропии.

1. Чем больше неопределённость выбора сообщений, тем больше энтропия. Неопределённость максимальна при равенстве вероятностей выбора каждого сообщения:

В этом случае

(4)

т.е. максимальная энтропия равна логарифму от объёма алфавита.

Например, при k=2(двоичный источник)

бит

2. Неопределённость минимальна, если одна из вероятностей равна единице, а остальные – нулю(выбирается всегда только одно, заранее известное сообщение, например - одна буква):

. В этом случае

Эти свойства энтропии иллюстрируются следующим образом.

Пусть имеется двоичный источник сообщений, т.е. осуществляется выбор из двух букв (k=2): x₁ и x₂ P(x₁)+P(x₂)=1

Тогда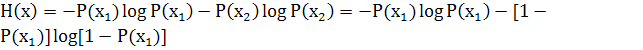

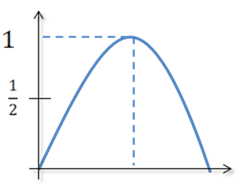
Зависимость H(x) от вероятностей выбора для двоичного источника приведена на рис.1

Рис. 1

3. Укрупним алфавит. Пусть на выходе двоичного источника имеется устройство, которое группирует буквы в слова из n букв. Тогда k=2ⁿ слов(объём алфавита). В этом случае

бит

Таким образом, укрупнение алфавита привело к увеличению энтропии в n раз, так как теперь уже слово включает в себя информацию n букв двоичного источника. Тем самым доказывается свойство аддитивности энтропии.

4. Энтропия дискретного источника не может быть отрицательной.

Термин “энтропия” заимствован из термодинамики и применительно к технике связи предложен К. Шеноном, в трудах которого были заложены основы теории информации(математической теории связи).

3. Энтропия дискретного источника с зависимыми сообщениями

Ранее при определении энтропии предполагалось, что каждое сообщение (буква или слово) выбирается независимым образом. Рассмотрим более сложный случай, когда в источнике сообщений имеются корреляционные связи. В так называемом эргодическом источнике выбор очередной буквы сообщения зависит от каждого числа предшествующих n букв. Математической моделью такого источника является марковская цепь n-го порядка, у которой вероятность выбора очередной буквы зависит от n предшествующих букв и не зависит более ранних, что можно записать в виде следующего равенства:

(7)

где c – произвольное положительное число.

Если объём алфавита источника равен K, а число связанных букв, которые необходимо учитывать при определении вероятности очередной буквы, равно порядку источника n, то каждой букве может предшествовать M=Kⁿ различных сочетаний букв(состояний источника), влияющих на вероятность появления очередной буквы x_i на выходе источника. А вероятность появления в сообщении любой из K возможных букв определяется условной вероятностью (7) с учётом предшествующих букв, т.е. с учётом M возможных состояний. Эти состояния обозначим как q₁, q₂,..q_m.

Рассмотрим два простых примера.

Пример 1. Пусть имеется двоичный источник(объём алфавита k=2), выдающий только буквы a и b; порядок источника n=1. Тогда число состояний источника M=K¹=2¹=2(назовём эти состояния q₁ и q₂). В этом случае вероятности появления букв a и b будут определяться следующими условными вероятностями:

P(a/q₁=a), P(a/q₂=b),

где: q₁=a – 1^е состояние источника

q₂=b – 2^е состояние источника

т.е. P(q₁)=P(a); P(q₂)=P(b)

Пример 2. Пусть по-прежнему K=2(буквы a и b), однако число связанных букв n=2. Тогда M=2²=4(четыре возможных состояния): (a,a)=q₁, (a,b)=q₂, (b,a)=q₃, (b,b)=q₄

В этом случае имеем дело со следующими условными вероятностями

P(a/a,a); P(a/a,b); P(a/b,a); P(a/b,b); P(b/a,a)… и т.д. Вероятности состояний определяются равенствами P(q₁)=P(a,a), P(q₂)=P(a,b), P(q₃)=P(b,a), P(q₄)=P(b,b).

Энтропия эргодического дискретного источника определяется в два этапа:

1) Вычисляется энтропия источника в каждом из M состояний, считая эти состояния известными:

для состояния q₁
q₂

………..……………………………..….… q_m

2) Далее находим H(x) путём усреднения по всем состояниям q;

(8)

При наличии корреляционных связей между буквами в эргодическом источнике энтропия уменьшается, т.к. при этом уменьшается неопределённость выбора букв и в ряде случаев часть букв можно угадать по предыдущим или ближайшим буквам.

4. Избыточность источника

Как было показано ранее, энтропия максимальна при равновероятном выборе элементов сообщений и отсутствии корреляционных связей. При неравномерном распределении вероятностей и при наличии корреляционных связей между буквами энтропия уменьшается.

Чем ближе энтропия источника к максимальной, тем рациональнее работает источник. Чтобы судить о том, насколько хорошо использует источник свой алфавит, вводят понятие избыточности источника сообщений: ячс& (9)

или

&

Наличие избыточности приводит к загрузке канала связи передачей лишних букв сообщений, которые не несут информации (их можно угадать и не передавая).

Однако, преднамеренная избыточность в сообщениях иногда используется для повышения достоверности передачи информации – например, при помехоустойчивом кодировании в системах передачи информации с исправлением ошибок любой язык, в том числе и русский или английский имеет избыточность до 50%. Благодаря избыточности обеспечивается понимание речи при наличии дефектов в произношении или при искажениях речевых сигналов в каналах связи.

5. Производительность источника

Производительность источника определяется количеством информации, передаваемой в единицу времени. Измеряется производительность количеством двоичных единиц информации (бит) в секунду. Если все элементы сообщения имеют одинаковую длительность τ, то производительность

, [Бит/с] (10)

Если же различные элементы сообщения имеют разную длительность, то в приведённой формуле надо учитывать среднюю длительность τ, равную математическому ожиданию величины τ:

Однако в последней формуле P(τ_i) можно заменить на P(x_i) (вероятность i-того сообщения), т.к. эти вероятности равны. В результате получаем

(11)

а производительность источника будет равна

(12)

Максимально возможная производительность дискретного источника равна

(13)

Для двоичного источника, имеющего одинаковую длительность элементов сообщения (k=2, =τ) имеем

бит/с (14)

При укрупнении алфавита в слова по n букв, когда k=2ⁿ, =nτ, имеем

бит/с, что совпадает с (14)

Таким образом, путём укрупнения алфавита увеличить производительность источника нельзя, так как в этом случае и энтропия, и длительность сообщения одновременно возрастают в одинаковое число раз (n).

Увеличить производительность можно путём уменьшения длительности элементов сообщения, однако возможность эта ограничивается полосой пропускания канала связи. Поэтому производительность источника можно увеличить за счёт более экономного использования полосы пропускания, например, путём применения сложных многоуровневых сигналов

где m – основание кода

6. Совместная энтропия двух источников

Пусть имеется два дискретных источника с энтропиями H(x) и H(y) и объёмами алфавитов k и l (рис. 2)

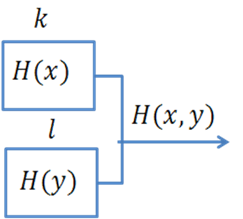
Рис. 2

Объединив оба эти источника в один сложный источник и определим совместную энтропию. Элементарное сообщение на выходе системы содержит элементарное сообщение x_i и сообщение y_i. Алфавит сложной системы будет иметь объём K.L, а энтропия будет равна

(15)

или

(16)

По теореме умножения вероятностей

Подставляя эти соотношения в (15), получим (17)

Аналогично можно получить

(18)

Здесь H(x) и H(y) – собственная энтропия источников x и y

(19)

-условная энтропия источника y относительно источника x. Она показывает, какую энтропию имеют сообщения y, когда уже известно сообщения x.

Если источники независимы, то

P(y/x)=P(y) и H(y/x)=H(y). В этом случае H(x,y)=H(x)+H(y).

Если источники частично зависимыми, то H(x,y)<H(x)+H(y).

Если источники полностью зависимыми(x и y – содержат одну и ту же информацию), то H(y/x)=0 и H(x,y)=H(x)=H(y).

7. Взаимная информация источников сообщений

На рис.3 показана(условно) собственная энтропия H(x) и H(y), условные энтропии H(x/y) и H(y/x) и совместная энтропия H(x,y). Из этого рисунка, в частности, следует соотношения (17) и (18)

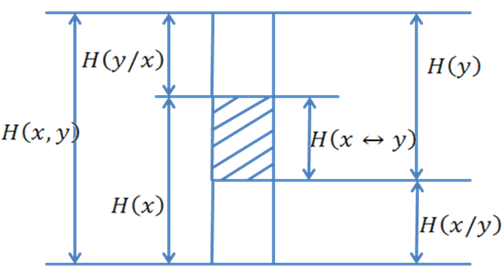
Рис. 3

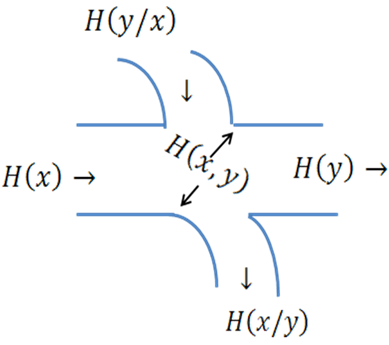
Рис. 4

Часть рисунка, отмеченная штриховкой, называется взаимной информацией H( ). Она показывает, какое(в среднем) количество информации содержит сообщение x о сообщении y(или наоборот, сообщение y о сообщении x).

Как следует из рис. 3

H(x↔y)=H(x)-H(x/y)=H(y)-H(y/x) (20)

Если сообщения x и y полностью независимы, то взаимная информация отсутствует и H(x )=0. Если x и y полностью зависимы (x и y содержат одну и ту же информацию), то H( )=H(x)=H(y). Понятие взаимной информации очень широко используется в теории передачи информации. Требования к взаимной информации различны в зависимости от того, с какой информацией мы имеем дело. Например, если x и y – это сообщения, публикуемые различными газетами, то для получения возможно большей суммарной(совместной) информации взаимная (т.е. одинаковая в данном случае) информация должна быть минимальной. Если же x и y – это сообщения на входе и на выходе канала связи с помехами, то для получения возможно большей информации её получателем необходимо, чтобы взаимная информация была наибольшей. Тогда условная энтропия H(x/y) – это потери информации в канале связи (ненадежность канала). H(x/y) – энтропия шума(помех) равная H(ξ), т.е. H(y/x)=H(ξ) .

8. Скорость передачи и пропускная способность канал связи

В дискретной системе связи при отсутствии помех информация на выходе канала связи (канала перед. информац.) полностью совпадает с информацией на его выходе, поэтому скорость передачи информации численно равна производительность источника сообщений:

(21)

При наличии помех часть информации источника теряется и скорость передачи информации оказывается меньше, чем производительность источника. Одновременно в сообщении на выходе канала добавляется информация о помехах (рис. 5)

Рис. 5

Поэтому при наличии помех необходимо учитывать на выходе канала не всю информацию, даваемую источником, а только взаимную информацию.

(22)

На основании формулы (20) имеем

или

(23)

где H’(x) – производительность источника.

H’(x/y) – “ненадёжность” канала (потери) в ед. времени

H’(y) – энтропия выходного сообщения в ед. времени

H’(y/x)=H’(ξ) – энтропия помех (шума) в ед. времени

Пропускной способностью канала связи (канала передачи информации) C называется максимально возможная скорость передачи информации по каналу.

C=maxR(x,y) (24)

Для достижения максимума учитываются все возможные источники на входе и все возможные способы кодирования.

Таким образом, пропускная способность канала связи равна максимальной производительности источника на входе канала, полностью согласованного с характеристиками этого канала, за вычетом потерь информации в канале из-за помех.

В канале без помех , т.к. . При использовании равномерного кода с основанием m состоящего из n элементов длительностью τ_э, в канале без помех

C=max (25)

при m=2, c= бит/сек

Для эффективного использования пропускной способности канала необходимо его согласование с источником информации на входе. Такое согласование возможно как для каналов без помех, так для каналов связи с помехами на основании двух теорем, доказанных К. Шенноном.

1-ая теорема (для канала связи без помех)

Если источник сообщений имеет энтропия H(x)(бит на символ), а канал связи – пропускную способность C (бит в секунду), то можно закодировать сообщение таким образом, чтобы передавать информацию по каналу со средней скоростью, сколь угодно близкой к величине C, но не превзойти её.

К. Шеннон предложил и метод такого кодирования, который получил название статического или оптимального кодирования. В дальнейшем идея такого кодирования была развита в работах Фано и Хоффмена и в настоящее время широко используется на практике для “сжатия сообщений”.

2-ая теорема (для каналов связи с помехами)

Если пропускная способность канала равна C, а производительность источника H’(x)<C, то путём соответствующего кодирования можно передавать информацию со скоростью, сколь угодно близкой к C и с вероятностью ошибки сколь угодно близкой к нулю. При H’(x)>C такая передача невозможна.

К сожалению, теорема К. Шеннона для канала с шумами(помехами) указывает только на возможность такого кодирования, но не указывает способа построения соответствующего кода. Однако, известно, что при приближении к пределу, устанавливаемому теоремой Шеннона, резко возрастает время запаздывания сигнала в устройствах из-за увеличения длины кодового слова n. При этом вероятность же ошибки на выходе сигнала стремится к величине

(26)

Очевидно, что P_экв→0,когда и τ_экв→∞, и, следовательно, имеет место “обмен” вероятности передачи на скорость и задержку передачи.

9. Статистическое кодирование дискретных сообщений

Используя теорему К. Шеннона, сформулированную в предыдущем разделе, можно увеличить производительность источника дискретных сообщений, если априорные вероятности различных элементов сообщения неодинаковы, К.Шеннон предложил и метод такого кодирования, который получил название статистического или оптимального кодирования. В дальнейшем идея такого кодирования была развита в работах Фано и Хаффмена и в настоящее время широко используется на практике для "сжатия сообщений".

Основой статистического (оптимального) кодирования сообщений является теорема К. Шеннона для каналов связи без помех.

Кодирование по методу Шеннона-Фано-Хаффмена называется оптимальным, так как при этом повышается производительность дискретного источника, и статистическим, так как для реализации оптимального кодирования необходимо учитывать вероятности появления на выходе источника каждого элемента сообщения (учитывать статистику сообщений).

Используя определения производительности и избыточности дискретного источника, приведённые можно получить

Из этой формулы видно, что для увеличения производительности нужно уменьшать избыточность χ или среднюю длительность сообщений .

Идея статического кодирования заключается в том, что, применяя неравномерный неприводимый код, наиболее часто встречающиеся сообщения (буквы или слова) кодируются короткими кодовыми словами этого кода, а редко встречающиеся сообщения кодируются более длительными кодовыми словами.

Рассмотрим принципы оптимального кодирования на приводимом ниже примере. Пусть источник сообщений выдаёт 8 различных сообщений x1…x8 с вероятностями 0,495; 0,4; 0,026; 0,02; 0,018; 0,016; 0,015; 0,01 (сумма вероятностей равна 1).

Располагаем эти сообщения столбцом в порядке убывание вероятностей.

{x_i, p(x_i)} Кодовое дерево Код N_i p(x)N_i

------------- ---------------------------

x₁ 0,495 0 1 0,495

x₂ 0,4 10 2 0,8

x₃ 0,026 1100 4 0,104

x₄ 0,02 1110 4 0,08

x₅ 0,018 11010 5 0,09

x₆ 0,016 11011 5 0,08

x₇ 0,015 11110 5 0,075

x₈ 0,01 11111 5 0,05

------------- ---------------------------

Рисунок 6 - Статистическое кодирование

Объединяем два сообщения с самыми минимальными вероятностями двумя прямыми и в месте их соединения записываем суммарную вероятность: p(x7)+p(x8)=0,015+0,01=0,025. В дальнейшем полученное число 0,025 учитываем в последующих расчётах наравне с другими оставшимися числами, кроме чисел 0,015 и 0,01. Эти уже использованные числа из дальнейшего расчёта исключаются. Далее таким же образом объединяются числа 0,018 и 0,016, получается число 0,034, затем вновь объединяются два минимальных числа (0,02 и 0,026) и т.д.

Построенное таким образом кодовое дерево используется для определения кодовых слов нового кода. Напомним, что для нахождения любого кодового слова надо исходить из корня дерева (точка с вероятностью 1) и двигаться по ветвям дерева к соответствующим сообщениям x1…x8. При движении по верхней ветви элемент двоичного кода равен нулю, а при движении по нижней - равен единице. Например, сообщению x5 будет соответствовать комбинация 11010. Справа от кодового дерева записаны кодовые слова полученного неравномерного кода. В соответствии с поставленной задачей, наиболее часто встречающееся сообщение x1 (вероятность 0,495) имеет длительность в 1 элемент, а наиболее редко встречающиеся имеют длительность в 5 элементов. В двух последних столбцах рисунка приведено число элементов Ni в кодовом слове и величина произведения p(xi)Ni=∑ p(xi)Ni= 1,774 представляет собой число элементов, приходящееся на одно слово, т.е. в данном случае .

Если бы для кодирования был применён равномерный двоичный код, который чаще всего применяется на практике, число элементов в каждом кодовом слове для кодирования восьми различных сообщений равнялось бы трём (2³=8), т.е. ..В рассматриваемом примере средняя длительность кодового слова благодаря применённому статистическому кодированию уменьшилась в 3/1,774=1,72 раза. Во столько же раз увеличилась и производительность источника.

Дальнейшим развитием оптимального статистического кодирования является кодирование кодовых слов. В этом методе применяется также оптимальное кодирование по методу Шеннона-Фано-Хаффмена, однако не к отдельным буквам, а к кодовым словам( сочетаниям n букв первичного сообщения). Статистическое кодирование слов позволяет ещё больше уменьшить среднюю длительность сообщений, так как алфавит источника быстро увеличивается с увеличением длины слова. Число возможных кодовых слов (алфавит источника после объединения букв) определяется выражением m=kⁿ, где k - алфавит букв первичного сообщения. Пусть, например, у нас имеется двоичный источник с алфавитом a₁и a₂(например, “1” и “0”). При передаче этих букв по каналу связи используются сигналы длительностью τ_э, а =τ_э.

Рассмотрим пример, когда p(a₁)=0,8 и p(a₂)=0,2 (если вероятности p(a₁)и p(a₂)равны между собой, никакое кодирование не может уменьшить среднюю длительность сообщения). Образуем из элементов a₁ и a₂слова из двух букв (n=2), беря различные сочетания из этих букв. Если у нас источник с независимым выбором элементов сообщений, то

p(a₁a₁)=0,8*0,8=0,64;

p(a₁a₂)= p(a₂a₁)=0,8*0,2=0,16;

p(a₂a₂)=0,2*0,2=0,04.

Применяя к полученным словам кодирование по методу Шеннона-Фано-Хаффмена, получаем кодовое дерево (рисунок 2.6), из которого видно, что новые кодовые слова неравномерного кода имеют длительность τ_э, 2τ_э и 3τ_э.

Средняя длина кодового слова

τ_сл=0,64τ_э+0,16*2τ_э+0,16*3τ_э+ 0,04*3τ_э=1,56τ_э.

Но так как каждое слово содержит информацию о двух буквах первичного сообщения, то в расчёте на 1 букву получаем τэ, Отсюда видно, что средняя длина элемента сообщения сократилась по сравнению с первоначальной в 1/0,78=1,38 раза.

a₁a₁

a₁a₂

a₂a₁

a₂a₂

Рисунок 7 – Алфавит источника после объединения букв

Если усложнить кодирование и использовать n=3, то в этом случае получим . Это уже почти предел, дальше уменьшать n уже нецелесообразно. Чтобы убедиться в этом, рассчитаем производительность источника сообщений для всех трёх случаев. Энтропия источника

бит.

Последняя величина близка к предельно возможной величине 1/ τ_э.

Статистическое кодирование слов целесообразно применять также в случае использования эргодического дискретного источника (источника с корреляционными связями букв), так как объединение букв в слова приводит к разрушению корреляционных связей (величина n должна быть не менее порядка эргодического источника, а nτ_э, соответственно, больше интервала корреляции букв первичного сообщения). Корреляционные связи между буквами трансформируются в различные вероятности появления возможных слов (n - буквенных сочетаний). При этом необходимо помнить, что вероятность n-буквенных сочетаний определяется не произведением вероятностей отдельных букв, а, в соответствии с теоремой умножения вероятностей надо учитывать также условные вероятности. Так, например, для источника с независимым выбором букв p(a₁a₁)=p(a₁)p(a₁), эргодического источника с корреляционными связями букв p(a₁a₁)=p(a₁)p(a₁/a₁).

10. Энтропия непрерывного источника и её свойства

Энтропия дискретного сигнала определялась выражением (2). Для непрерывной случайной величины воспользуемся эти же выражением, заменив вероятность P(x) на W(x)dx

В результате получим

Но логарифм бесконечно малой величины (dx) равен минус бесконечности, в результате чего получаем

H(x)=∞-

Таким образом, энтропия непрерывной случайной величины бесконечно велика. Но т.к. в последнем выражении первое слагаемое (∞) от величины x или от W(x) не зависит, при определении энтропии непрерывной величины это слагаемое отбрасывают, учитывая только второе слагаемое (некоторою “добавку” к бесконечности). Эта добавочная энтропия определяемая формулой

(27)

называется дифференциальной энтропией непрерывной случайной величины.

В дальнейшем слово “дифференциальная” в определении энтропии будем иногда опускать. Как и для дискретных сообщений, существуют следующие разновидности дифференциальной энтропии непрерывной величины.

1. Условная энтропия случайной величины у относительно случайной величины x

, или

(28)

2. Совместная энтропия двух непрерывных случайных величин равна

, или

(29)

Для независимых x и y H(x,y)=H(x)+H(y). Для совместной дифференциальной энтропии непрерывной случайной величины справедливы соотношения (17) и (18)

H(x,y)=H(x)+H(y/x)

H(x,y)=H(y)+H(x/y)

3. Взаимная информация H(x↔y) содержащаяся в двух непрерывных сигналах x и y, определяется формулой (20)

Для независимых x и y H(x↔y)=0

4. Если случайная величина ограничена в объёме V=b-a, то её дифференциальная энтропия максимальна при равномерном законе распределения этой величины

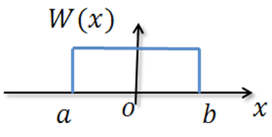
Рисунок 8

Так как эта величина зависит только от разности (b-a), а не зависит от абсолютных величин b и a, следовательно, H_max(x) не зависит от математического ожидания случайной величины x.

5. Если случайная величина не ограничена в объёме (т.е. может изменяться в пределах от -∞ до +∞), а ограничена только по мощности, то дифференциальная энтропия максимальна в случае гаусcовского закона распределения этой величины. Определим этот максимум в соответствии с (27)

W(x)=

отсюда

Но математическое ожидание m{(x-a)²}= , отсюда получаем

или окончательно

(30)

Следовательно, энтропия зависит только от мощности δ². Эта важная формула будет использоваться позднее для определения пропускной способности непрерывного канала связи.

Замети, что, как и ранее, H_max(x) не зависит от математического ожидания a случайной величины x. Это важное свойство энтропии. Оно объясняется тем, что мат. ожидание является не случайной величиной.

11. Пропускная способность непрерывного канала связи

Если x(t)-сигнал на входе канала связи, а y(t)=x(t)+ς(t) – сигнал на его выходе(ς(t)-аддитивная помеха), то скорость передачи информации по непрерывному каналу связи будет определяться выражением (23), в котором величину 1/τ надо заменить на 2F_max=2F_k

(31)

где, как и ранее, H(y) – это энтропия выходного сообщения, H(y,x) – энтропия шума(почему она так называется, будет видно из дальнейшего изложения).

Пропускная способность равна максимально возможной скорости передачи по каналу связи, когда источник сигнала полностью согласован с характеристиками канала связи:

(32)

Максимум H(y) достигается в случае гаусcовского закона распределения величины y. При этом:

(33)

При учёте влияния помехи необходимо рассматривать наихудший случай, когда помеха распределена также по гаусcовскому закону. Условная вероятность P(y/x) – это попросту плотность вероятности W(y/x) случайной величины y при якобы известном заранее x является случайной. Но, так как, y(t)=x(t)+ξ(t) можно записать

,

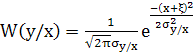где - дисперсия величины y при известном x, т.е. дисперсия помехи .

Определим условную энтропию H(y/x)

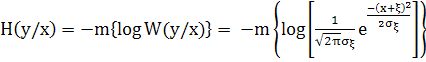
В этом выражении предполагается, что x известно заранее. Таким образом, величина x в приведенном выражении является попросту математическое ожидание величины y. Однако известно, что энтропия непрерывного случайного процесса от математического ожидания не зависит. Тогда получаем

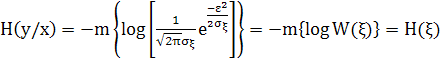
отсюда видно, почему условная энтропия H(y/x) называется энтропией шума.

Для гауссовского закона распределения помехи максимальное значение энтропии шума, в соответствии (30) будет равно

(34)

Подставляя (33) и (34) в (32) получаем

(35)

Перенося число 2 под знак логарифма, получим . В этом выражении - мощность помехи, а , где P_c – мощность сигнала на выходе канала связи. С учётом этого получаем окончательно формулу для вычисления пропускной способности непрерывного канала связи(формулу Шеннона):

(36)

В заключении отметим следующее. Для достижения скорости передачи информации по непрерывному каналу связи, близкой к пропускной способности канала связи, сигнал x(t) по статической структуре должен быть близок к флуктуационной помехе (белому шуму) с гауссовским законом распределения.

12. Эпсилон-энтропия источника непрерывных сообщений

Сигнал на выходе источника (И) непрерывных сообщений (например, микрофона, телефона, датчика температуры и пр.) представляет собой непрерывный случайный процесс, энтропия которого в любом из сечений в общем случае равна бесконечности. Такое количество информации не может быть передано по реальному каналу связи, пропускная способность которого всегда ограничена. Это и не нужно, так как скорость восприятия информации любым потребителем на выходе канала всегда ограничена его физическими возможностями. Поэтому непрерывный сигнал на выходе канала связи даже без помех отличается от сигнала на входе, так как содержит не всю информацию о нём (причём под каналом связи можно понимать любое преобразование одного ансамбля сигналов в другое: модуляцию, усиление, дискретизацию и пр.). Уже преобразование непрерывного сообщения в сигнал соответствующим устройством (микрофоном или др. датчиком сигнала) связано с потерей части информации, а сигнал отображает сообщении лишь с некоторой точностью

где x(t) - сигнал на входе преобразователя; – сигнал на выходе преобразователя (Пр) или оценка входного сигнала преобразователем, который всегда представляет собой некоторое решающее устройство, работающее по определенному правилу и заданному критерию качества.

Критерий качества, как известно, определяется потребителем информации, например, среднеквадратическое отклонение

или дисперсия ошибки

Эпсилон-энтропией H_ε(x)(ε-энтропией) называется минимальное количество информации, которое должно содержаться в выходном сигнале о входном сигнале x(t), чтобы этот сигнал можно было восстановить с заданной точностью ε_ср.

где

I(x, )-взаимная информация x и ;

h(x) и h(x/ )-соответственно, дифференциальная энтропия сигнала x(t) и условная энтропия x(t), когда известно; min и max берутся по всевозможным условным ФПВ w(x/ ).

В общем случае, когда сигнал (или сообщение) x(t) является гауссовским с дисперсией , ошибка ε(t) также является гауссовской с дисперсией , а с учётом аддитивного характера ошибки ε(t) условная энтропия h(x/ ) полностью определяется дифференциальной энтропией h(ε). Соответственно, maxh(x/ )=maxh(ε)= .

Тогда ε – энтропия одного сечения гауссовского источника(ε – энтропия одного отсчёта)

h_ε(x)= - =0,5 .

Величина показывает отношение мощности(дисперсии) сигнала x(t) к мощности(дисперсии) ошибки, при котором среднеквадратическое отклонение сигналов x(t) и не превышает .

Следовательно, производительность источника непрерывных сообщений можно определить как количество информации, которое необходимо передавать в единицу времени, чтобы восстановить сообщение с заданной точностью.

h_ε(x)=vh_ε(x),

где v=1/ - скорость передачи отсчетов на выходе источника, – интервал между отсчетами.

Для стационарного сигнала с ограниченным спектром =1/(2F_max), тогда h_ε(x)=2F_max h_ε(x).

Если, кроме того, что источник является гауссовским, то

h_ε(x)= F_max .

Количество информации, выдаваемое гауссовским источником за время T_c, равно T_c h_ε(x)= T_cF_max , что совпадает с формулой для объёма сигнала, когда динамический диапазон сигнала

D_c= .

Это значит, что объём сигнала на выходе источника равен количеству информации, которое содержится в сигнале для его воспроизведения с заданной точностью.

Для канала с пропускной способностью C, на выходе которого подключен источник с производительностью h_ε(x), теорема К. Шеннона для канала с шумами принимает вид:

Если при заданном критерии точности источника (например, ) его эпсилон-производительность меньше пропускной способности канала h_ε(x)<C, то существует способ кодирования (преобразования сигнала), при котором неточность воспроизведения сколь угодно близка к ; при h_ε(x)>C такого способа не существует.

Теорема К. Шеннона определяет предельные возможности согласования источника непрерывных сообщений с каналом связи. Практически это достигается применением помехоустойчивых видов модуляции и кодирования.