9.1. Недостатки обычных линий передачи и преимущества волноводов

9.1.1. Типы волноводов

9.2. Особенности направляемых волн

9.3. Волновые уравнения полей в волноводе произвольного сечения

9.4. Классификация ЭМВ

9.4.1. Е - волны

9.4.2. Н - волны

9.5. Прямоугольный волновод

9.5.1. Основная волна в прямоугольном волноводе. Преимущества волны Н₁₀

9.5.2. Токи в стенках волновода

9.5.3. Передача энергии по волноводу

9.5.4. Потери энергии в волноводе

9.5.5. Е - волны в прямоугольном волноводе

9.6. Круглые волноводы

9.6.1. Волны "Е" - типа в круглом волноводе

9.6.2. Волны "H" - типа в круглом волноводе

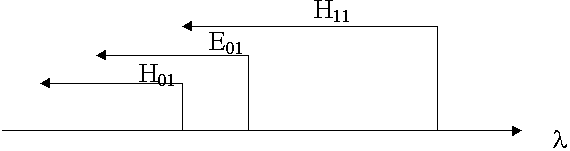
9.6.3. Волна Н₀₁ в круглом волноводе. Применения ее в дальней cвязи

9.7. Волноводы сложного сечения

9.8. Возбуждение волноводов

Под направляющей системой понимают устройство, ограниченное в двух измерениях и осуществляющее передачу ЭМ энергии в третьем измерении. Волны, которые распространяются в таких направляющих системах получили название - направляемые электромагнитные волны. Такие направляющие системы называются волноводами.

9.1. Недостатки обычных линий передачи преимущества волноводов

Широкое развитие получили двухпроводные и коаксиальные линии еще в прошлом веке.

Недостатки: В 2-х проводных и коаксиальных линиях резко возрастает затухание энергии с ростом частоты. Факторы:

1. Поверхностный эффект в проводниках приводит к росту потерь с ростом частоты 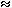f ^1/2.
2. Диэлектрические потери. С ростом f диэлектрические потери увеличиваются пропорционально f 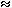f.
3. Излучение. В 2-х проводной линии эффект излучения очень значителен мощность излучения пропорционально квадрату f ~ f².

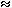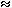В двухпроводных линиях при 1 м и короче потери такие больше, что ее нецелесообразно применять; на _ген = 3 м, затухание в коаксиальном кабеле в среднем 0,2 дБ/м _ген = 10 см затухание 2 дБ/м, т.е. ничего не дойдет от передатчика к антенне.

Из двухпроводной линии можно сделать волновод, но так не делают на практике, только на бумаге, как в детском конструкторе. Входное сопротивление отрезка длиной имеет бесконечно большое значение:

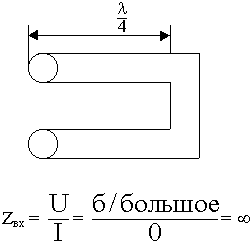
Если подключить отрезок к линии, то он никак не повлияет, т.к. 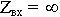. И так сколько угодно можно подключить таких отрезков. Получили волновод.

Достоинства:

• Трубка жесткая. Простая конструкция.
• Фактор диэлектрических потерь исключается.
• Фактор излучения - исключается.
• Плотность токов значительно меньше, т.к. они распределены по всем стенкам.
• Можно передать большие мощности.

Академик Капица подсчитал, что в трубе (круглой) диаметром 1 м. можно передать всю мощность Красноярской ГЭС.

9.1.1. Типы волноводов

Различают 2 типа:

- односвязные волноводы,
- двухсвязные волноводы.

Порядок связности определяется тем, что поле распределено в какой-то области и не с чем не связано.

Используются и сложные формы сечения.

Все это односвязные волноводы.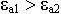

Волны могут распространятся вдоль диэлектрических стержней. Их называют диэлектрическими волноводами, а в оптике - световодами. Металла вообще нет.

К 2-х связным системам относится коаксиальный волновод. Поле определяется уже двумя проводниками.

9.2. Особенности направляемых ЭМВ

Рассмотрим идеально проводящую плоскость, на которую под некоторым углом падает плоская ЭМВ.

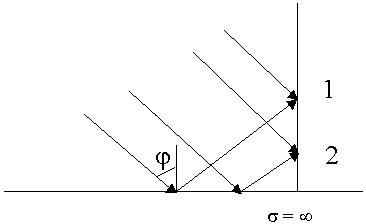
Выясним, как распределено ЭМП над плоскостью, если на нее падает ЭМВ. В т.1 поступает отраженная волна и додающая. В каждой точке над металлической плоскостью ЭМП определяется суперпозицией полей падающих и отраженных. Результат суперпозиции зависит от того, в каких фазах эти поля складываются. Там где фазы одинаковы, будет max, где в противофазе будет min. Из граничных условий. Касательная составляющая вектора Е должна обращаться в 0, поэтому вторую плоскость располагаем в нулях. Физическая основа передачи энергии по волноводам связана с многократным отражением ЭМВ от идеально проводящих стенок. В волноводах могут распространяться ЭМВ с различной структурой поля. Угол j зависит от частоты. С уменьшением частоты угол j уменьшается.

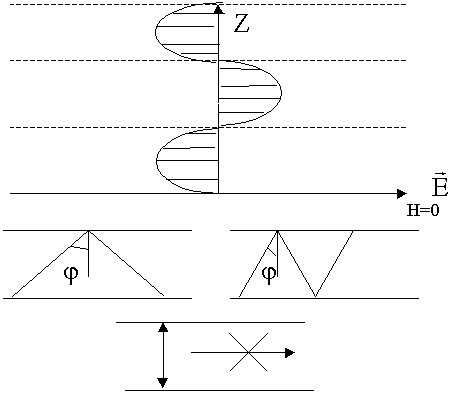
Выводы:

Из качественного рассмотрения. В волноводе существует минимальная частота (критическая f_кр). Ниже этой критической частоты энергию по волноводу передавать нельзя f = f_кр (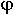 = 0) .

Пример: Если по трубе подать световые волны в критическом режиме, то в конце трубы будет темно. При f 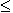f_кр энергия не передается.

Покажем, что V_ф всегда > С.

Перемещение фронта одинаковых фаз не совпадает с осью волновода. Почему так происходит ? Волна идет под углом многократно отражаясь.

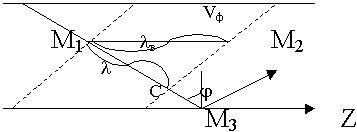
Направление распространения волны из т. М₁ в т. М₂ показано. Волна распространяется со скоростью света. В т. М₁ был 0, через длину волны в т. М₂ тоже 0 (расстояние равное ). За это же самое время вдоль оси расстояние будет пройдено другое (фазовый фронт тот же). Чтобы в т. М₃ прийти с той же фазой волне надо двигаться с большей скоростью.

Вывод: _в всегда > , V_ф всегда > С.

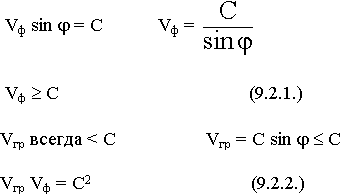
При распространении ЭМВ всегда появляется продольная составляющая либо Е либо Н.

9.3. Волновые уравнения полей в волноводе произвольного сечения

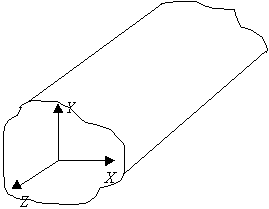
Стенки трубы идеально проводящие. Среда с параметрами 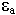, 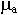неизменна. Генератор, источник сторонних полей далеко вынесен. Тогда в любой точке этого волновода справедливы уравнения Максвелла:

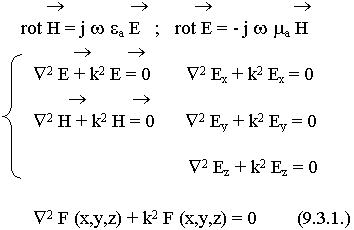
Под F понимаем любую проекцию (Е_х Е_я и т.д.).

Как можно решить такое уравнение ? Много методов. Один из наиболее удобных - метод разделения переменных по Фурье. Идея метода Фурье заключается в том, что решение ищется в виде произведения функций, каждая из которых зависит от одной из координат. Энергия в волноводе распространяется вдоль оси Z, это обстоятельство мы учтем, выделив функциональную зависимость от Z.

F (x,y,z) = f (x,y) Ф (z) (9.3.2.)

Поскольку решение записано в такой форме, оно должно удовлетворять уравнению.

Проверка:

Ф (z)(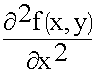)+ Ф (z)( 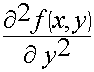) + f (x,y) (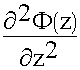)+ k² f (x,y) Ф (z) = 0

(9.3.3.)

Разделим все члены уравнения на коэффициент при k²

(f (x,y) Ф (z))

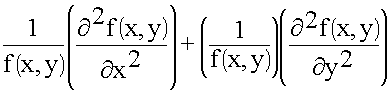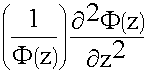+ = - k²

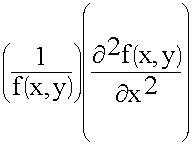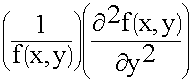+=-k²_s (9.3.4.)

Индекс “S” означает, что поля изменяются только в поперечных координатах. Это поперечное волновое число.

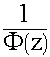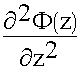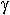. = ² - продольное волновое число

k² = k²_s + 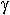² (9.3.5.)

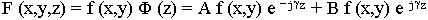
для общего случая

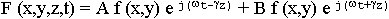
(9.3.6.)

Общее решение представляет собой два волновых процесса с амплитудами А и В и одинаковым распределением поля в поперечном сечении (f (x,y)) и распространяющихся в противоположных направлениях. Поскольку волновод бесконечно длинный, отраженной волны нет, В = 0. Нет физических условий для возникновения отраженной волны. Общая запись полей для произвольного сечения волновода:

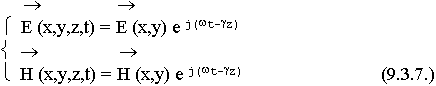
Для конкретизации задаются 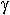, Е (х,у) Н (х,у)

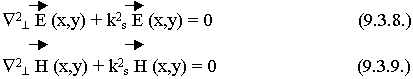
В общем виде уравнения не решаются.

Установим связь между в свободном пространстве, _в и _кр.

В свободном пространстве волновое число:

k = (9.3.10.)

Продольное волновое число = (9.3.11.)

Поперечное волновое число k_s = (9.3.12.)

k² = k_s² + ² ()² = (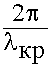)² + ()² (9.3.13.)

_в = 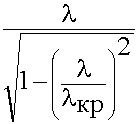(9.3.14.)

если умножить на f правую и левую часть уравнения (9.3.14) получим:

V_ф = _в f = 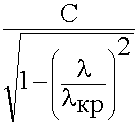(9.3.15.)

9.4. Классификация ЭМВ

В основе классификации лежит критерий - наличие или отсутствие одной из продольных составляющих. Классификация волн позволяет упростить анализ волн в волноводе и записать все составляющие полей через одну составляющую. Установим связь между поперечными составляющими полей и продольными. Для этой цели спроектируем уравнения Максвелла на оси координат:

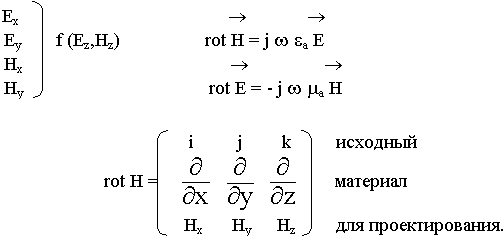
Проекции на оси х, у, z:

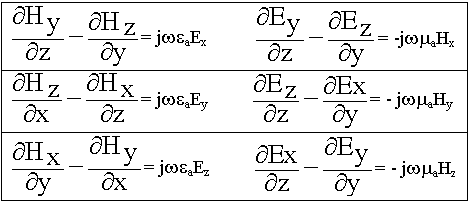
(9.4.1.)

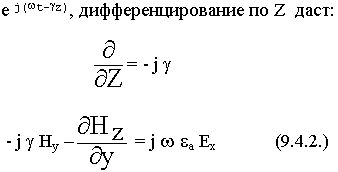
Начнем с уравнения (9.4.2.). Из поперечных составляющих имеем Е_х и Н_у. Эти же составляющие имеем в (9.4.6.). Из (9.4.2.) находим Н_у и подставляем в уравнение (9.4.6.). В результате подстановки составляющие Е_х, Е_у, Н_х, Н_у будут выражены следующим образом:

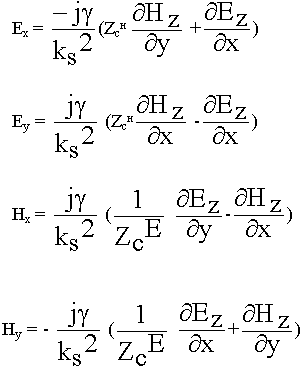
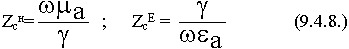
Эти соотношения показывают, что отличные от 0 поперечные составляющие полей в волноводе имеют место, когда одна из продольных составляющих обращается в 0. Различают 4 класса полей.

Первый класс - Электрические волны.

Для этого класса Е_z 0 , H_z = 0 (Е - волны)

Второй класс - Магнитные волны.

Для этого класса H_z 0 , E_z = 0 (Н - волны)

Третий класс - Поперечные волны, Т - волны.

H_z = 0 , E_z = 0 (пример плоская ЭМВ)

Четвертый класс - Гибридные волны.

E_z 0 , H_z 0 (такие волны характерны для световода).

Конкретизируем связь поперечных и продольных составляющих для каждого класса.

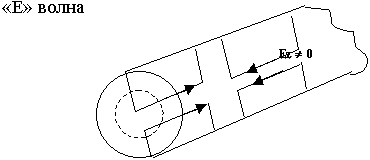
9.4.1. Е - волны

Е_z 0 , H_z = 0

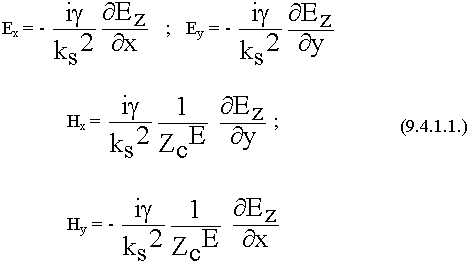
Смысл классификации:

Для расчета полей достаточно найти продольную составляющую.

9.4.2. Н - волны

E_z = 0 , H_z 0

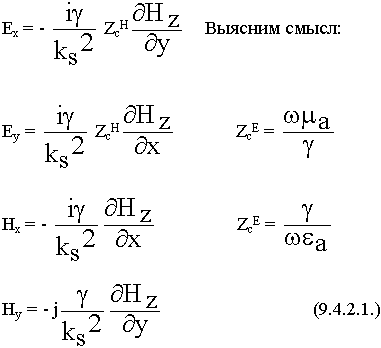
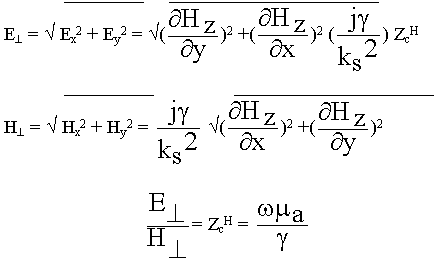
= Z_c^H- называют характеристическим сопротивлением Н - волны.

Аналогично для волны типа Е:

= Z_c^E = 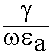- характеристическое сопротивление волны типа Е. (9.4.2.2.)

Что произойдет, если Е_z = 0, H_z = 0 ? “Т - волна”. Отличные от 0 поперечные составляющие могут существовать только в одном случае, когда k_s = 0, тогда неопределенность (0/0) может дать при раскрытии конечное число.

k_s = 0 _кр = =

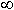
Волна “Т” существует в таких линиях передачи, в которых может поддерживаться устойчивое распределение электрических и магнитных полей в поперечном сечении волновода.

Пример: “Т” волна в коаксиальной линии

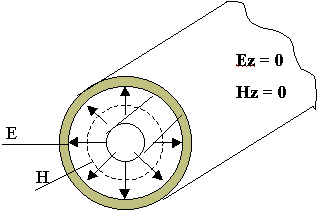
Коаксиальная линия обладает таким свойством. Существует “Т” волна. По такой линии можно передать и постоянный и переменный ток.

Если будет заряд, он создает поле, которое растекается по поверхности.

Убираем внутренний проводник. Пустая труба. Переменное электрическое поле будет порождать переменное магнитное поле. В поперечном сечении устойчивое распределение полей создать нельзя. В полых трубах волны “Т” распространяться не могут, а только Е, либо Н. В двух связных системах “Т” волны.

9.5. Прямоугольный волновод

Это металлическая труба прямоугольного сечения.

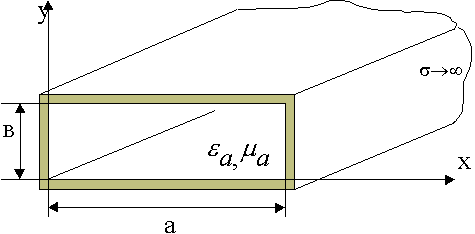
Задача:

1) найти распределение полей.
2) найти _кр

Знаем, что все поля в волноводе можно рассчитать через продольную составляющую.

“Н” - волны в прямоугольном волноводе.

Требуется найти H_z:

1) H_z = ? 2) E_x , E_y , H_x , H_y - находим через H_z все остальные. 3) конкретизация полей по выполнению граничных условий.

Составляющая Н_z удовлетворяет волновому уравнению.

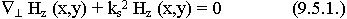
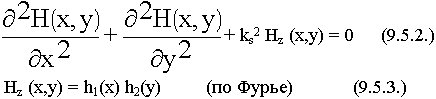
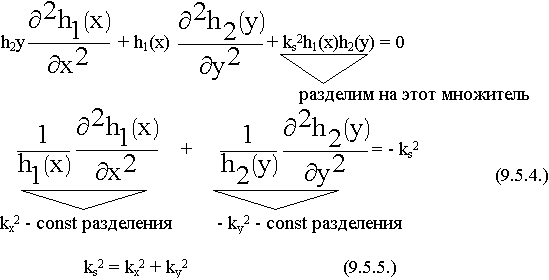
const разделения будем называть поперечными волновыми числами.

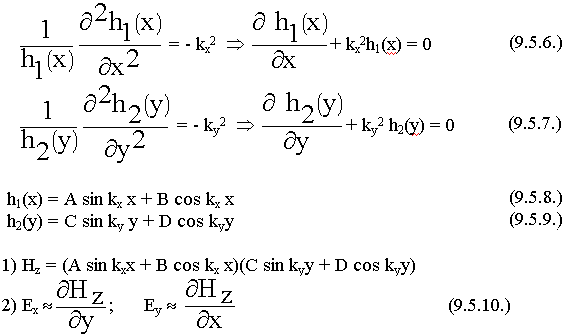
3) Запишем граничные условия для данной задачи.

а) E_x = 0 при у = 0 ; y = b

б) Е_у = 0 при х = 0 ; x = a

E_x 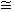(A sin k_xx + B cos k_xx) k_y (C cos k_yy - D sin k_yy) (9.5.11.)

Накладываем граничные условия:

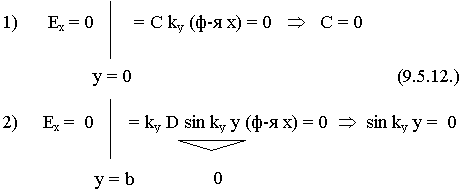
const D нельзя приравнивать к 0, т.к. исчезнет поле H_z, значит sin k_yy = 0

k_yb = n ; k_y =

n = 0, 1, 2 . . . (9.5.13.)

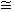
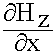
3) E_y 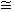таким же образом можно показать, что const А = 0 из условия

Е_у = 0 при х = 0 (9.5.14.)

4) Е_у = 0 при х = а

k_x = (9.5.15.)

m = 0, 1, 2 . . .

H_z(x,y) = H₀ cos () x cos () y^.е^{j(w t-g z)} ; H₀ = B D (9.5.16.)

В рамках задачи нельзя определить Н₀, т.к. не задана мощность волны на входе. Окончательно другие составляющие полей.

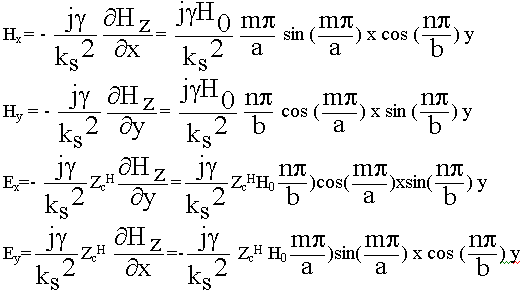
Составляющие Н_х, Н_у, Е_х, Е_у умножаем на е^{j(w t-g z)} (9.5.17.)

Соотношения (9.5.5.), (9.5.13.), (9.5.15.) позволяют определить _кр.

_кр =; k_s² = k_x² + k_y² = ()² + ()²

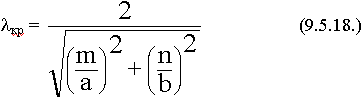
Каждому набору значений индексов m и n соответствует свое распределение поля в волноводе, своя критическая длина волны Н_mn. Минимальные значения индексов если m = 0, n = 0, но поля нет. Одновременно индексы не могут быть равны нулю, по частям возможно.

m = 0, 1, 2, 3 . . .

n = 0, 1, 2, 3 . . .

Индексы m и n определяет распределение поля по координатам х, у. С учетом периодичности функции cos, число m имеет смысл - количество полуволн, укладывающихся вдоль а, n - число полуволн, укладывающихся вдоль b. Условием распространения волны в волноводе, является ^ген < _кр. В волноводе бесчисленное множество волн, но не все эти волны могут распространяться. Распространяются только те, которые удовлетворяют условию: ^ген < _кр

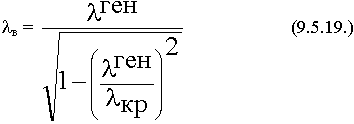
_в – длина волны в волноводе.

_кр зависит от размеров поперечного сечения а и b, и значения индексов m и n. Максимальная _кр будет для индексов m = 1, n = 0, т.е. волны, у которой значения индексов минимальны.

a > b ; m = 1 , n = 0

Максимальной _кр, обладает волна Н₁₀* _кр = 2а. У всех других волн критическая длина волны меньше, волну Н₁₀ называют основной волной в волноводе. Она наиболее часто используется.

Выделим ось, где откладываем .

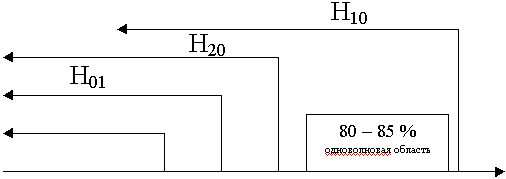
Диаграмма спектра волн в прямоугольном волноводе.

Если ^ген > 2a, то волны не распространяются.

m = 1, n = 0 Н_{10 кр} = 2а

m = 2 , n = 0 H₂₀ , _кр = а

m = 0 , n = 1 H₀₁ , _кр = 2b

Стандартный волновод 2b < a для волны Н₁₀:

a ^ген 2a - одноволновый режим.

Диапазон использования одноволновой области 80 - 85 %. Не рекомендуется подходить к критическому режиму (справа и слева).

Предположим, имеем прямоугольный волновод, на входе этого волновода имеется генератор СВЧ диапазона и возбудитель волны.

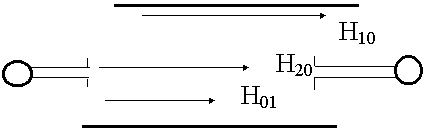
Возбудитель может возбудить любую волну (Н₁₀, Н₂₀ и т.д.). На выходе стоит похожее устройство, принимающее сигнал индикатора. Эксперимент заключается в следующем: генератор перестраивается в широком диапазоне частот.

Если ^ген > 2а , индикатор ничего не показывает, энергия не идет по волноводу.
^ген 2а Н₁₀
^ген < а Н₂₀ часть энергии идет на волне Н₂₀
(условно из 10 Вт генер. 8 Вт передается волной Н₂₀)
^ген < 2b H₀₁

Специалисту нужно, чтобы была одна волна, для этого нужно уменьшать поперечное сечение волновода (частота генератора остается неизменной).

В реальных условиях нереально создать условия, когда волны существуют в волноводе независимо друг от друга. Многоволновое распространение нежелательно, т.к. информация из канала в канал передается. Стараются избежать взаимной связи между волнами и использовать одноволновый режим. Волна - mode - по английски. Говорят одномодовый, многомодовый.

9.5.1. Основная волна в прямоугольном волноводе. Преимущества волны Н₁₀

• Имеет место максимальный диапазон одноволновой передачи.
• При передаче энергии на волне Н₁₀ потери энергии волны минимальны.
• Поперечные размеры волновода наименьшие при передаче волны типа Н₁₀.

Выпишем составляющие волны Н₁₀

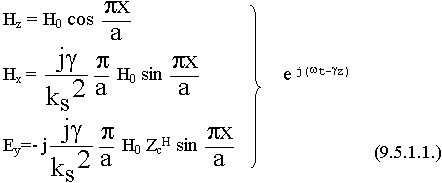
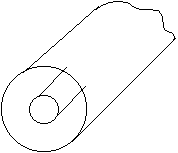
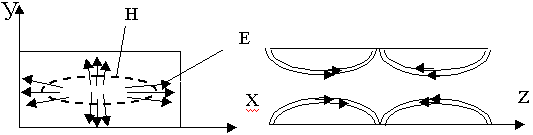
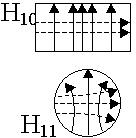
Восстановим из уравнений распределение силовых линий Е и Н поля для основной волны. Рассмотрим поперечное сечение волновода.

Электрическое поле волны Н₁₀ имеет одну составляющую Е_у, она max в середине волновода.

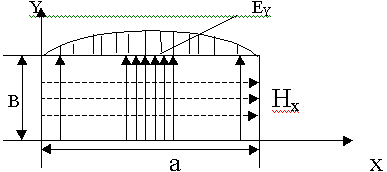
Поле Е направлено от одной стенки к другой. Магнитное поле имеет 2 составляющие Н_х и Н_z.

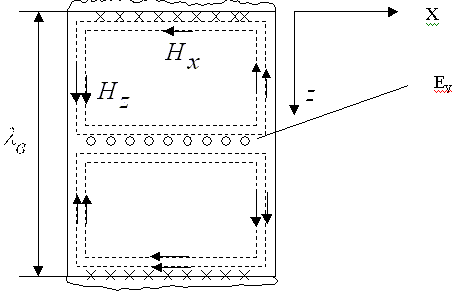
У боковых стенок волновода Н_Z максимальна. В силу непрерывности линий магнитного поля Н_z замыкается через Н_х (Н_z переходит в Н_х). Эта картинка перемещается в волноводе со скоростью:

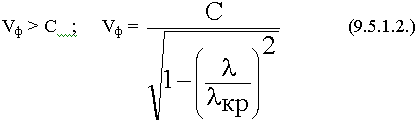
9.5.2. Токи в стенках волновода

В силу закона электромагнитной индукции переменное магнитное поле вблизи проводников возбуждает электрический ток. Переменное магнитное

поле вблизи стенок будет создавать токи проводимости. Посмотрим как протекают токи ? Знание токов позволяет решить 2 задачи:

• Рассчитать потери в волноводе.
• Определить как осуществить разрез стенок, чтобы из волновода извлечь энергию, либо наоборот, не нарушать распределения токов.

Установим связь между плотностью поверхностных токов и напряженностью магнитного поля. Разберем простейший случай.

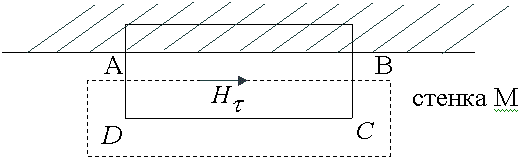
Вблизи стенки волновода магнитное поле всегда имеет только касательную составляющую. Применим закон полного тока к контуру, часть которого находится в металле, часть нет.

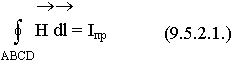
определим по частям:

^ABCD

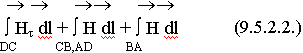
Предположим контур мал, Нt всегда перпендикулярна СВ, АD. Участок АВ находится в глубине металла. В силу поверхностного эффекта токи поверхностные быстро затухают. Значение магнитного поля на участке ВА очень мало. Этот интеграл обращается в 0.

Для малых АВСD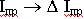

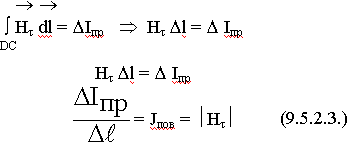
Плотность поверхностного тока числено равна касательной составляющей магнитного поля и они взаимно перпендикулярны.

Чтобы восстановить распределения токов надо воспользоваться разверткой.

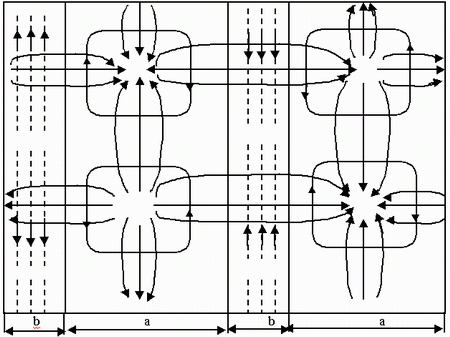
Составляющая Н_х порождает ток J _z. В широкой стенке 2 тока, продольный J_z, поперечный J_y. В боковой стенке поперечные токи J_y.

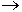Н_х J_z , H_z J_x

Если щель в волноводе пересекает токи, то такая щель будет хорошо излучать, если щель вдоль токов, то она не излучает. Щели 1, 2 - не излучают; 3,4 - излучают.

9.5.3. Передача энергии по волноводу

Рассмотрим процесс передачи энергии на примере основной волны Н₁₀:

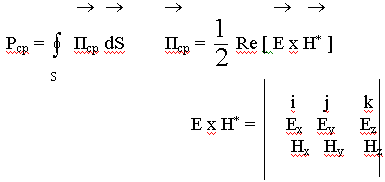
П_{z ср} = Е_х Н_у^* - Е_уН_х^* = - Е_у Н_х ^. Энергия, передаваемая вдоль волновода определяется только поперечными составляющими полей. (9.5.3.1.)

-E_yH_x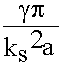^* =()² H₀² Z_c^H sin²() (9.5.3.)

Вычислим теперь среднюю мощность:

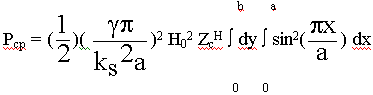
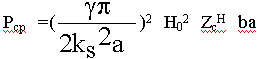средняя мощность, передаваемая в волноводе. (9.5.3.3.)

Передаваемая мощность по волноводу зависит от амплитуды продольной составляющей магнитного поля Р_ср 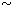Н₀² . Мы можем увеличить передаваемую мощность, увеличивая размеры волновода. Найдем Н₀:

H₀ = 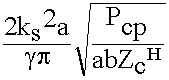(9.5.3.4.)

Эта составляющая числено равна поперечному току в стенках волновода. Она возбуждает в стенках волновода ей ток.

Н₀ = | J_x| = | J_y|

E_y = - (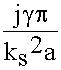) Z_c^H H₀ sin

E_y0 = 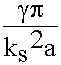Z_c^H (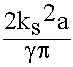) 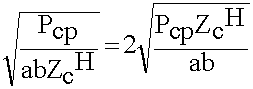^. > (9.5.3.5.)

Напряженность электрического поля возрастает с ростом передаваемой по волноводу мощности.

Е_проб^max 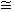30 для воздуха

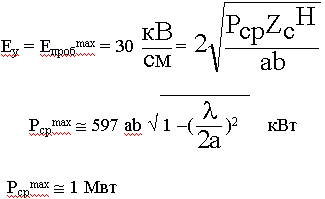
a , b - см.

a x b = 2,3 x 1,0 см Р_ср^max 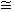1 Мвт

При проектировании различных устройств обязательно делают запас прочности:

Р_раб = (0,2 ¸ 0,3 ) Р_ср^max

Один из путей повышения уровня передаваемой мощности связан с заполнением его средой, имеющей более высокое значение пробивного напряжения, чем у воздуха.

9.5.4. Потери энергии в волноводе

Можно выделить 3 основных фактора, которые несут ответственность за потери энергии:

• Конечная проводимость стенок волновода. За счет этого часть токов в стенках волновода преобразуется в тепло, греет волновод (омические потери).
• Несовершенство среды, которая заполняет волновод (диэлектрические потери).
• Связан с нарушением однородности стенок. Из-за непрерывной эксплуатации или других факторов образуются какие-то щели и через них проходит излучение энергии.

Любая из этих причин приводит к тому, что 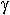- постоянная распространения величина комплексная, как и в случае плоских волн.

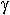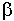= - j;

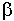- фазовая постоянная

- коэффициент затухания.

Предположим, что имеется отрезок волновода.

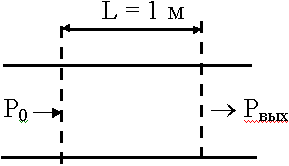
На входе Р₀, на выходе Р_вых. Сколько теряется энергии ?

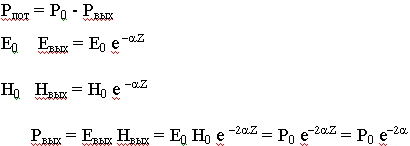
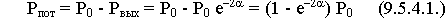
В случае, когда параметр << 1, тогда:

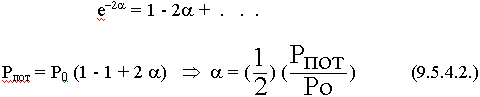
Основным фактором потерь являются омические потери.

Нужно собрать все потери в стенках волновода:

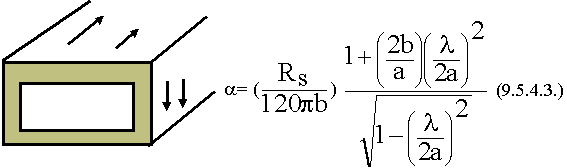
R_s - поверхностное сопротивление.

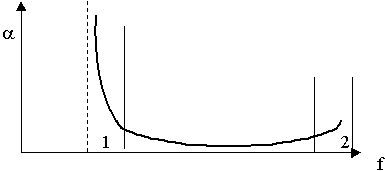
В области (1) потери большие, так как частота близка к критической. А дальше с ростом частоты растет поверхностное сопротивление металла, т.е. работает поверхностный эффект. Расчет по формуле (9.5.4.3.) дает чуть меньше коэффициент затухания, чем на самом деле. Поскольку мы не учитываем качество обработки поверхности. Для уменьшения потерь нужно высокое качество обработки и материал с максимально большой проводимостью. С этой целью используется покрытие стенок серебром. Реально достижимые потери (0,1 ¸ 0,01 ) дБ/м.

Волновод, заполненный диэлектриком

R_s =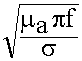

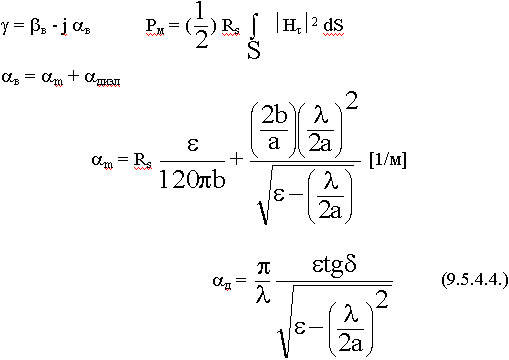
9.5.5. Е - волны в прямоугольном волноводе

Наряду с волнами Н - типа, в прямоугольном волноводе могут распространяться волны Е- типа. Анализ волн проводится по той же схем, что и в случае Н - волн.

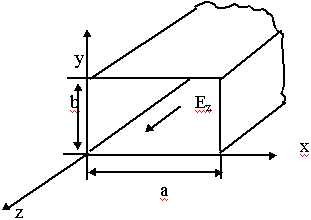
Е - волны Е_z 0, H_z = 0

Решается уравнение:

Результатом решения будет:

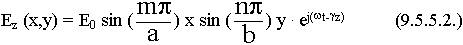
Запись удовлетворяет граничным условиям на стенках волновода.

m = 1, 2, 3 . . . m 0

n = 1, 2, 3 . . . n 0

Если одно из чисел m или n обращается в 0, то волны не будет.

Е_e = 0 при х = 0, х = а, Е_х = 0 при у = 0, у = b.

Каждому набору индексов m и n соответствует своя структура поля в поперечном сечении, каждая из волн имеет свою _кр.

_кр = 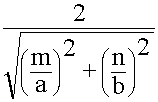(9.5.5.3.)

Выражение (9.5.5.3.) совпадает с выражением (9.5.18) для Н - волн. Волны Н и Е с одинаковыми индексами m и n имеют одно значение _кр и V_ф. Пример: Н₁₁, Е₁₁ - одинаковые _кр , V_ф. Волны, имеющие одинаковые V_ф, _кр, но различные структуры в поперечном сечении называются вырожденными.

У волны Е индексы m и n не равны 0. У “Н” один из индексов может быть равен нулю. Из “E” - волн самая простая Е₁₁.

Магнитное поле для волн типа Е всегда в плоскости поперечного сечения волновода, т.к. линии Е всегда перпендикулярны Н.

Для волн “Е” характерно присутствие Е_z вдоль оси Z. Волноводы с волной “Е” используются в ускорителях и в электровакуумных приборах (в тех случаях, где необходимо осуществить взаимодействие элементарных частиц с электромагнитным полем).

9.6. Круглые волноводы

Представляют собой металлическую трубу круглого сечения. Для изучения полей в каждой точке надо применить цилиндрическую систему координат.

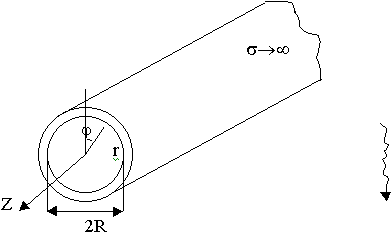
Особенности: своеобразная запись граничных условий. Внутри поверхности, любая касательная составляющая (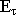 = 0) электрических полей должна обращаться в 0. Требования для граничных условий.

1) = 0 при r = R.

2) 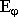= 0 при r = R.

9.6.1. Волны “Е” типа в круглом волноводе

Е_z 0, H_z = 0

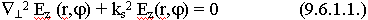
Это уравнение должно решаться в цилиндрических координатах.

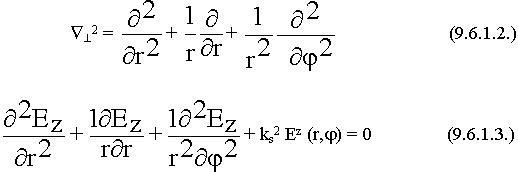
Решаем по м. Фурье с разделением переменных:

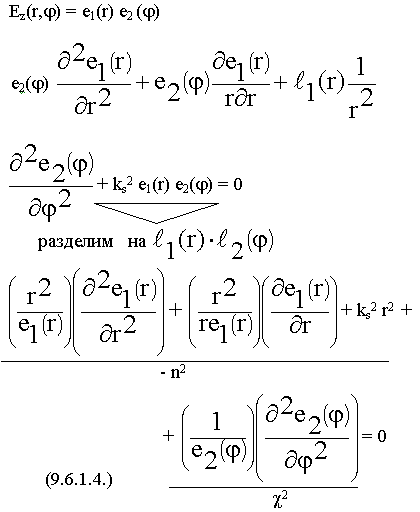
Результат разделения: n² = ² – константы разделения

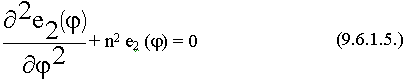
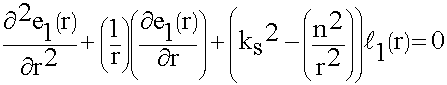(9.6.1.6.)

Поделим на r².Решением первого уравнения ( 9.6.1.5.) являются тригонометрические функции. Из (9.6.1.5.):

е₂() = A sin n + B cos n (9.6.1.7.)

Решением уравнения (9.6.1.6.) являются функции Бесселя и Неймана:

J_n - функция Бесселя.

N_n - функция Неймана.

У функций Бесселя есть значения аргументов, при которых функции обращаются в 0. Эти значения называют корнями.

_nm

n - порядок функции Бесселя.

m - порядковый номер корня.

Поскольку в любой точке поля должны быть конечны, то коэффициент D = 0, т.к. функция Неймана может давать бесконечно большое значение функции:

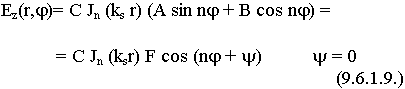
Начало отсчета угла можно начать с любого места:

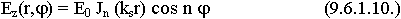
Выясним, какие значения принимает “n” - распределение поля по азимуту. Сделав оборот по углу j на 360⁰ мы попадаем в ту же точку, значения полей не должны изменяться. Из условий периодичности параметр n всегда целое число (n = 0, 1, 2). Для нахождения _кр используем граничные условия по составляющим Е_z. Е_z (r, ) при r = R должно быть равно нулю.

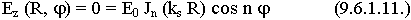
Это возможно в одном случае, когда значение аргумента равно корню функции:

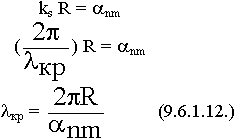
Значения корней функции Бесселя затабулированы. Минимальным значением корня обладает функция Бесселя нулевого порядка ₀₁.

₀₁ = 2,405 ; _кр = 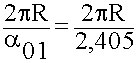=2,61 R = _кр (9.6.1.13.)

Каждому значению n и m соответствует свое распределение поля. Первый индекс указывает сколько полуволн укладывается по азимуту, а второй по радиусу (диаметру).

Простейшая волна Е₀₁.

Е₁₁ 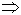Е₀₁ преобразуется волна Е₁₁ в прямоугольном волноводе в волну Е₀₁ круглого волновода. При деформации стенок волновода, линии вектора Е всегда перпендикулярны проводнику.

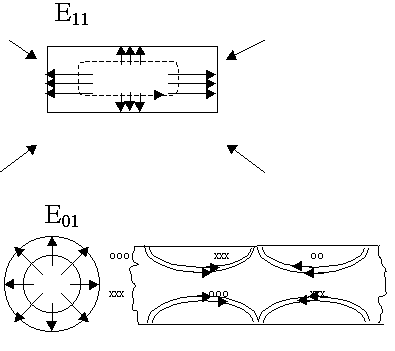
Волна Е₀₁ называется симметричной. Используется во вращающихся сочленениях радиолокационных станций.

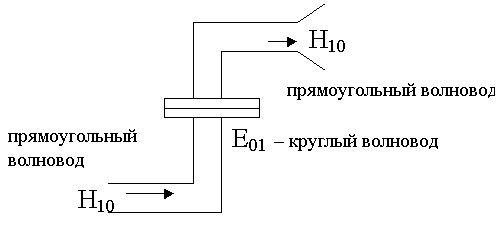
Вращающееся сочленение в радиолокационных станциях.

9.6.2. Волны “Н” типа в круглом волноводе

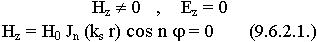
Граничные условия в случае волны типа Н:

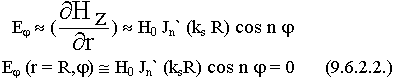
Это требование выполняется, когда значение аргумента k_sR равно корню производной функции Бесселя.

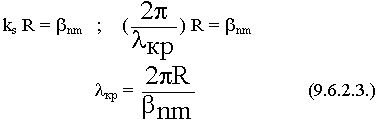
Каждому значению n и m соответствует своя структура, своя _кр.

_кр^max при n = 1 , m = 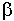₁₁ = 1, 84 _кр = 3,41 R

Волна Н₁₁ - является основной волной круглого волновода. Волну Н₁₁ можно получить путем деформации волны Н₁₀ в прямоугольном волноводе.

9.6.3. Волна Н₀₁ в круглом волноводе. Возможности применения ее в дальней связи

Н₀₁ - симметричная магнитная волна соответствует значению корня функции Бесселя 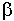₀₁ = 3,83 ;

_кр = 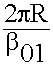= 1,64 R

Критическая длина волны ( _кр) у Н₀₁ меньше чем у Н₁₁ и Е₀₁. По отношению к волнам Н₁₁ и Е₀₁ волна Н₀₁ является высшей.

Структура поля Н₀₁

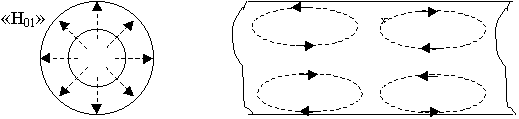
У волны Н₀₁ имеет место аномальные поведение затухание в зависимости от частоты.

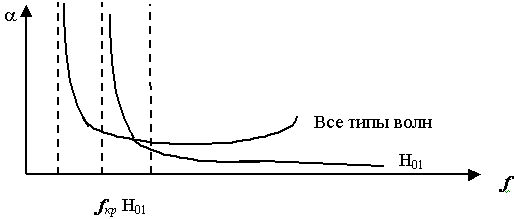
Для специалистов связи, это большое преимущество. С увеличением частоты расширяется возможность увеличения числа каналов. Увеличивается дальность связи за счет уменьшения потерь.

Почему происходит уменьшение затухания от частоты? Затухание связано с токами в стенках волновода.

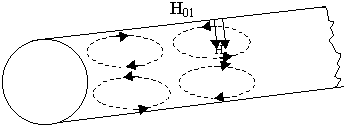
У стенок волновода находится продольная составляющая Н_z. Как токи направлены ? Линии тока всегда перпендикулярны Н_z, значит есть только кольцевые токи в стенках волновода. Источником этих токов являются продольные составляющие магнитного поля Н_z.

Для всех волн характерно, что с увеличением частоты продольные составляющие полей Н_z и E_z убывают.

Физическое объяснение. У волн других типов существуют и продольные и поперечные токи, которые возбуждаются продольными и поперечными магнитными полями. Наличие продольных токов приведет к увеличению потерь.

Пример:

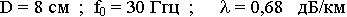
При усилении на 90 дБ длина усилительного участка L_ус = 130 км.

f₀ = 50 Ггц для тех же данных = 0, 28 дБ/км.

L_ус = 320 км

Основная трудность реализации идеи дальней связи заключается в том, что Н₀₁ является высшим типом. При D = 6 см и ₀ = 6 мм существует одновременно 300 типов волн.

Это неприятный момент. В реальных условиях происходит взаимодействие волн. Часть энергии волны Н₀₁ передается волнами других типов. Высшие типы волн быстро затухают, значит и часть энергии волны Н₀₁ - тоже затухает.

Вопрос: Как бороться с таким явлением ?

• В волноводе можно сделать пленку, которая оказывает сильное влияние на высшие типы и не оказывает на Н₀₁.
• В волноводе кольцевые токи. Можно сделать волновод из колец.

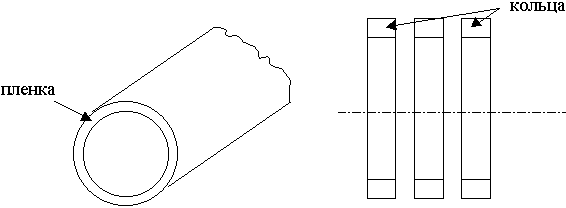
Для кольцевых токов Н₀₁ это не страшно, для других типов волн будет разрыв продольных токов. Наборный волновод сделать сложно, поэтому делают спиральный волновод. Созданы опытные волноводы.

Спектр волн в круглом волноводе.

9.7. Волноводы сложного сечения

Наибольшее применения нашли эллиптические волноводы. Идея пришла из биологии (рыба плывет извиваясь, но поперечное сечение не изменяется).

Достоинства эллиптических волноводов:

• Волновод можно наматывать на барабаны.
• Существует устойчивая поляризация передаваемой волны.

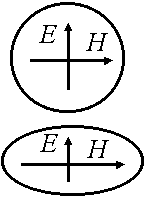
В режиме передачи и режиме приема строго должны быть выполнены условия неизменного поперечного сечения волновода.

В эллиптическом волноводе поляризация вертикальная и горизонтальная развязаны между собой.

“П” - образные волноводы.

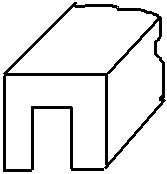
Достоинство волноводов:

• Обычно прямоугольный волновод имеет небольшую полосу рабочих частот.

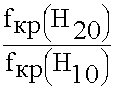= 2

Системы многоканальной связи работают в более широком диапазоне.

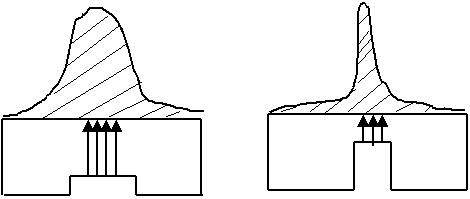
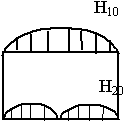
Введение выступа в широкой стенке не оказывает влияние на волну Н₂₀, на волну Н₁₀ оказывает сильное влияние. За счет концентрации поля можно увеличивать широкополосность.

= 5 ¸ 6

Недостатки “П” - образных волноводов:

• Сильная концентрация поля, плотность токов растет, потери возрастают.
• Может возникнуть пробой в месте большой концентрации поля. Падает передаваемая мощность.

9.8. Возбуждение волноводов

Возбуждение волноводов осуществляется с помощью элементарных электрических и магнитных излучателей.

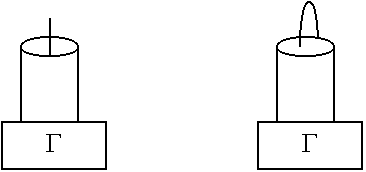
Для возбуждения волны в волноводе используется 3 принципа:

• Линии Е, создаваемые возбудителем, должны совпадать в некотором сечении волновода с линиями Е возбуждаемого типа волны.
• Линии Н, создаваемые возбудителем, совпадают с линиями типа Н возбуждаемого типа волны.
• Токи, создаваемые возбудителем, должны совпадать с токами в стенках волновода требуемого типа.

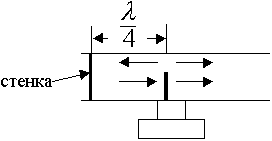
Если одно из условий удовлетворяется, то можно возбудить волну в волноводе, но это еще не гарантирует, что именно одна волна будет. В качестве возбудителя возьмем элементарный электрический излучатель.

Штырь параллелен вектору Е

1)

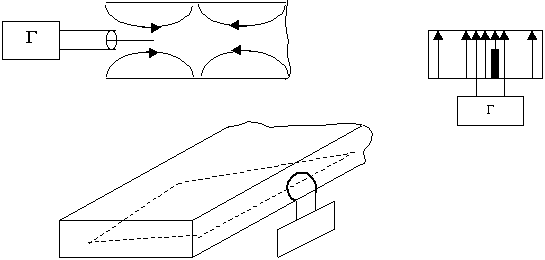
2)

Для того, чтобы от возбудителя волны распространялись в одну сторону, нужно поставить стенку на расстоянии . В этом случае будет синфазное сложение волн падающих и отраженных.