2.1. Исходные уравнения электродинамики

2.2. Плоские волны как простейший случай волнового процесса

2.1. Исходные уравнения электродинамики

Основные уравнения электродинамики поля, называемые уравнениями Максвелла, обобщают два основных закона электродинамики: закон полного тока и закон электромагнитной индукции.

Закон полного тока устанавливает количественное соотношение между напряженностью магнитного поля H и током :

, (2.1)

где j - объёмная плотность постоянного тока, протекающего в теле;

p - координаты;

n - вектор нормали, задающий положительное направление обхода контура L (как вращение правого винта с направлением движения по вектору);

Согласно данному закону линейный интеграл напряженности магнитного поля по замкнутому кругу равен полному току, проходящему сквозь поверхность, ограниченную этим контуром.

Уравнение (2.1) называется первым уравнением Максвелла.

Закон электромагнитной индукции (Фарадея) устанавливает соотношение между напряженностью электрического поля Е и магнитным потоком .Закон электромагнитной индукции гласит, что электродвижущая сила, возникающая в контуре при изменении магнитного потока , проходящего сквозь поверхность, ограниченную контуром, равна скорости изменения этого потока с обратным знаком:

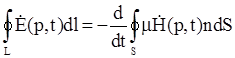(2.2)

Это уравнение называют вторым уравнением Максвеллом.

Уравнение (2.1) и (2.2) представляют собой интегральную запись уравнений Максвелла, чаще пользуются уравнениями в дифференциальной форме. При этом к левой части уравнений применяют известную формулу Стокса:

, .

Введём обозначение

,

где - где - удельная проводимость среды (См/м = 1/(Ом м).

С учетом этого::

(2.3),

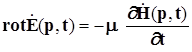, (2.4)

где - магнитная проводимость среды (Г/м, ).

Второе слагаемое в правой части уравнения (2.3) введено Максвеллом для учёта токов смещения в непроводящей среде

,

где - диэлектрическая проницаемость среды (Ф/м Ф/м).

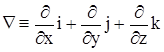
Понятие (rot) означает, что движение происходит по замкнутой кривой: спирали (, -(набла)).

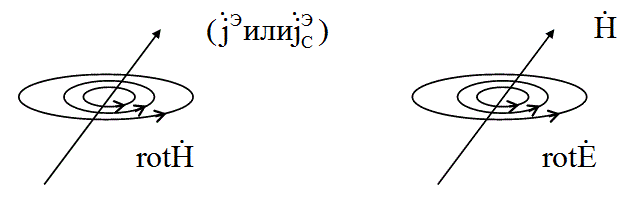
Заметим, что в интегральной форме направление движения задавало направление вектора нормали n.

Записанные уравнения обладают симметрией в следующем смысле: согласно первому уравнению изменение во времени электрической индукции порождает вихревое магнитное поле, вектор напряженности которого изменяется в пространстве, согласно второму уравнению изменение во времени магнитной индукции порождает вихревое электрическое поле, изменяющееся в пространстве. Из этого следует возможность существования электромагнитных полей в средах вдали от тел стоками проводимости. Электрические и магнитные поля могут существовать, взаимно порождая друг друга.

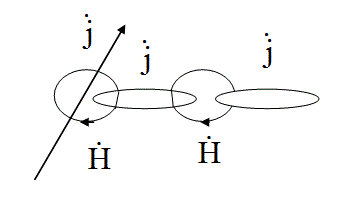
Кроме названных уравнений систему дополняют ещё два уравнения:

, (2.5),

где - плотность электрического заряда,

которые являются вспомогательными. ()

Из соотношений (2.5) первое означает, что через поверхность, ограничивающую некий объём, линии электрического поля расходятся в окружающее пространство или сходятся в него. Электрическое поле имеет источники и характеризуется плотностью электрического заряда. Второе уравнение выражает принцип непрерывности магнитного поля. Оно показывает, что магнитные линии всегда непрерывны и образуют замкнутые петли. Они нигде не начинаются и не заканчиваются. Магнитное поле не имеет источников.

Для гармонических колебаний:

и (2.6)

Тогда основные уравнения запишутся в виде:

(2.7)

.

Комплексная диэлектрическая проницаемость среды.

Первое уравнение может быть записано в виде:

(2.8)

где величину называют комплексной диэлектрической проницаемости среды.

Волновые уравнения в векторной форме. Уравнения Максвелла (2.8) образуют систему взаимосвязанных дифференциальных уравнений первого порядка, решение которых с учетом граничных условий в некотором случае весьма затруднительно. Для преодоления указанных трудностей переходят к более простой форме записи уравнений. Для её получения применяют к обеим частям уравнения (2.8) операцию rot. Отсюда, допустим для первого уравнения получают: (учитывая 2.9)

или

,

(Примечание: , но

; Следовательно К тому же .)

Обозначив в окончательном виде имеем:

. (2.9)

Величина определяется свойствами среды, в которой распространяются электромагнитные колебания и называется коэффициентом распространения среды. В общем случае это величина комплексная. Её действительная часть - характеризует процессы затухания в среде распространения и потому называется коэффициентом затухания. Величина - характеризует величину набега фазы и потому носит название коэффициент фазы.

Совершенно аналогично может быть получено второе уравнение относительно вектора напряженности электрического поля:

. (2.10)

Полученные уравнения (2.9) и (2.10) дают одинаковый закон изменения , и являются волновыми уравнениями в векторной форме.

Преимуществом этих уравнений их независимость от системы координат. Так как вектора и взаимосвязаны, то решение задачи распространения электромагнитных колебаний может быть найдено для одного из них, а за тем для другого получено путем учета их взаимосвязанности. ()

В математике уравнения вида (2.9) и (2.10) получили название уравнений Гельмгольца.

2.2. Плоские волны как простейший случай волнового процесса

Плоской называют такую волну при которой в электромагнитном поле можно провести ряд параллельных плоскостей, перпендикулярных направлению распространения волны так, чтобы векторы напряженности и в каждый момент времени лежали в этих плоскостях и сохраняли как своё значение так и своё направление. Основное свойство плоской волны взаимная перпендикулярность векторов и .

При плоской волне, распространяющейся вдоль оси z, с учетом того, что 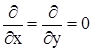, одно из уравнений например уравнение (2.11) приобретает вид:

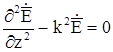. (2.11)

Общее решение уравнения (2.12) зависит только от координаты z, и определяется выражением:

, (2.12)

где и - постоянные интегрирования.

Оба слагаемые в уравнении (2.12) представляют плоские волны: одну бегущую (падающую волну) в направлении положительной оси z (выражение - ), другую в обратном направлении - отраженная волна (). Направление определяется выбором временного множителя .