Базовым элементом интегральной оптики является плоский оптический волновод, представляющий собой тонкий диэлектрический слой с показателем преломления п_в на подложке с показателем преломления п_п меньшим п_в. Поверх волноводного слоя может быть нанесен покровный слой с показателем преломления п_отакже меньшим п_в (в наиболее распространенном случае п_в > п_п > п_о). Обязательное требование к материалу оптического волновода (а также к подложке и покровному слою, как будет ясно из изложенного ниже) — оптическая прозрачность в используемом спектральном диапазоне и совершенство поверхностей раздела волноводной структуры.

Процессы, происходящие в плоском диэлектрическом волноводе, интерпретируются на основе геометрической (лучевой) оптики, которая по необходимости дополняется более общей волновой теорией.

В диэлектрическом волноводе толщиной порядка длины волны используемого света, находящейся обычно в пределах 0,1 —10 мкм, наблюдается ряд явлений, не рассматриваемых в обычной оптике, а аналогичных происходящим в диэлектрических радиоволноводах СВЧ-диапазона. В зависимости от соотношения показателей преломления п_в, п_п и п_о, а также от угла падения световой волны на границе раздела волна может либо канализироваться в волноводном слое (направленная, волноводная мода), либо выходить в подложку или покровный слой (излучательные, радиационные моды).

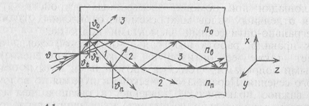
Рассмотрим планарную структуру, изображенную на рис. 4.1. На плоскую торцевую поверхность волноводного (световедущего) слоя направим луч света под углом θ к нормали. Часть световой энергии отразится от торцевой поверхности под углом, равным углу падения θ, а преломленная волна попадет в волноводный слой под углом преломления θ_t, связанным с углом θ законом преломления

(4.1)

(предполагается, что падающий луч распространяется в среде с п=1). При изменении угла θ должен также изменяться и угол падения на поверхность раздела волновода с подложкой и покровным слоем θ_В, причем θ_в = π/2 — θ_t если оба угла отсчитывать от нормалей к поверхностям раздела. Поскольку п_в больше n_п и n_о, то при достаточно больших углах θ_В (малых θ) имеет место явление полного внутреннего отражения, заключающееся в том, что преломления света на верхней и нижней границах волновода не происходит и вся энергия уносится отраженной волной, т. е. возвращается в оптически более плотную среду. Критический угол падения, больше которого наступает полное внутреннее отражение, зависит от соотношения показателей преломления материалов по обе стороны от поверхности раздела. Для верхней и нижней границ раздела при п_п ≠п₀ эти углы различаются и соответственно составляют

, (4.2)

, (4.3)

причем наиболее часто φ_о заметно меньше φ_п (значение п_В – п₀ составляет десятые доли или даже единицы, а п_В — п_П— всего 10^-2-10^-4).

Если угол падения луча на поверхность волновода θ_В меньше как φ_о, так и φ_п (луч 1 на рис. 4.1), полного внутреннего отражения не происходит ни на одной поверхности волноводного слоя. Свет будет частично отражаться от верхней его границы и частично преломляться, выходя в покровный слой или окружающее пространство. Отраженный от верхней границы свет, подойдя к нижней поверхности раздела, также частично отразится в волноводный слой, а частично преломиться в подложку. Это соответствует излучательной воздушной моде, хотя в рассмотренном случае часть световой энергии излучается в подложку.

Если же угол θ уменьшить так, что угол θ_В станет больше критического угла для границы раздела волновода с покровным слоем (воздухом) φ₀, определяемого (4.3), луч, распространяющийся в волноводе, испытает полное внутреннее отражение от верхней границы волновода, а от нижней отразится только частично. Таким образом, при φ_о<θ_в<φ_п световая энергия будет попадать преимущественно в подложку (мода подложки).

Наконец, при θ_В больше как φ₀, так и φ_п луч, попавший в волноводный слой, испытает внутреннее отражение не только на верхней, но и на нижней его поверхностях (волноводная мода).

Очевидно, что для канализации излучения угловые отклонения θ падающего на торец волновода пучка должны быть меньше, чем это соответствует равенству

, (4.4)

или, используя выражение (4.2) для φ_п, после преобразований обратных тригонометрических функций, получим

. (4.5)

Величину NA, определяемую (4.5), называют числовой апертурой волновода.

Волноводные моды являются практически наиболее важными, поскольку используются для передачи световой энергии вдоль волновода. Тем не менее свойства подложки и покровного материала влияют на волноводные моды. Это объясняется тем, что при полном внутреннем отражении световая волна проникает в оптически менее плотную среду—явление, называемое нарушенным полным внутренним отражением. Оно аналогично квантово-механическому туннелированию микрочастиц в область, где ее полная энергия меньше высоты потенциального барьера. Интенсивность проникающей за границу раздела световой волны экспоненциально убывает по мере удаления от границы, поэтому в качестве количественной характеристики нарушения внутреннего отражения используют некоторую эффективную глубину проникновения (расстояние, на котором интенсивность света убывает в е раз), значение которой зависит от угла падения и соотношения коэффициентов преломления контактирующих материалов. Применительно к рассматриваемой волноводной структуре эффективные глубины проникновения световой волны в покровный слой h₀ и подложку h_п соответственно составляют

(4.6)

(4.7)

т. е. суммарное эффективное увеличение толщины волноводного слоя (эффект Гуса — Хенхена) составляет h_o + h_П (ω — круговая частота, с—скорость света в вакууме).

Эффект Гуса-Хенхена важен не только потому, что приводит к увеличению эффективной толщины волноводного слоя по сравнению с его действительной (геометрической) толщиной h, но и в связи с тем, что в результате поглощения света в покровном слое и подложке (если только они не идеально прозрачны) коэффициенты отражения оказываются меньше единицы, т.е. полного отражения световой энергии нет. Согласно (4.6) и (4.7) глубина проникновения волноводной моды в подложку заметно больше, чем в покровный слой, поскольку п_В и п_П обычно отличаются мало. Поэтому для сведения к минимуму ослабления волноводной моды особенно важно, чтобы материал подложки был как можно более прозрачным.

При зигзагообразном распространении луча в плоском волноводе (рис. 4.1) расстояние, пройденное световой волной вдоль волновода, меньше длины траектории луча и особенно при малых углах θ_В. В связи с этим при описании волноводных мод вместо волнового числа k_λ=(ω/c)n_B вводят его составляющую вдоль направления распространения света, которую называют константой распространения

, (4.8)

а величину

(4.9)

называют эффективным показателем преломления волновода. Максимальное значение п_эф, очевидно, равно п_В(при θ_В = π/2), а минимальное — п_П, что соответствует условию существования волноводной моды θ_в=φ_п. Итак,

, (4.10)

что согласно (4.8) определяет пределы изменения константы распространения

. (4.11)

Для образования распространяющейся в диэлектрическом слое световой волны, кроме внутреннего отражения, должно выполняться также условие согласования фаз: фазовые сдвиги, накапливающиеся после двух отражений от верхней и нижней поверхностей волноводного слоя (на одном зигзаге), должны быть кратными 2π (если этого нет, волны интерферируют так, что гасят сами себя). Условие согласованности светового поля в плоском волноводе приводит к характеристическому уравнению

, (4.12)

где m = 0, 1, 2, ..., а ψ_о и ψ_п—сдвиги фаз на границах волновода с покровным слоем и подложкой соответственно. Решение уравнения (4.12) численными методами приводит к принципиально важному результату: для данной длины волны λ (частоты света ω) и толщины световодного слоя возможен дискретный набор значений угла падения волны на поверхности раздела θ_B = θ_m, т.е. в волноводном слое световая энергия переносится дискретными модами, каждой из которых соответствует угол θ_т и в согласии с (4.8) и (4.9) — эффективный показатель преломления п_ти константа распространения β_т(т называют модовым числом). Для данной λ существует некоторая минимальная (критическая) толщина h_кp, соответствующая только одной волноводной моде:

, (4.13)

где предполагается распространенный случай, когда п_В и п_Пмало отличаются, т. е. п_В+ п_П≡2п_В>>п_В — п_П= Δn. Если h<h_кp, канализации света в волноводном слое не происходит; при увеличении h по сравнению с h_кp появляется возможность существования двух, трех и т. д. волноводных мод; большему т соответствует мода с меньшим углом θ_т.