2.9.1. Двубинарная передача сигналов
2.9.2. Двубинарное декодирование
2.9.3. Предварительное кодирование
2.9.4. Эквивалентная двубинарная передаточная функция
2.9.5. Сравнение бинарного и двубинарного методов передачи сигналов
В 1963 году Адам Лендер (Adam Lender) [6, 7] показал, что с нулевой межсимвольной интерференцией можно передавать 2W символов/с, используя теоретическую минимальную полосу в W герц, без применения фильтров с высокой добротностью. Он использовал так называемый метод двубинарной передачи сигналов (duobinary signaling), также известный как корреляционное кодирование (correlative coding) и передача сигналов с частичным откликом (partial response signaling). Основной идеей, лежащей в основе двубинарного метода, является введение некоторого управляемого объема межсимвольной интерференции в поток данных, вместо того чтобы пытаться устранить ее полностью. Введя корреляционную интерференцию между импульсами и изменив процедуру обнаружения, Лендер, по сути, «уравновесил» интерференцию в детекторе и, следовательно, получил идеальное заполнение в 2 символа/с/Гц, что ранее считалось неосуществимым.
2.9.1. Двубинарная передача сигналов
Чтобы понять, как двубинарная передача сигналов вводит контролируемую межсимвольную интерференцию, рассмотрим модель процесса. Операцию двубинарного кодирования можно рассматривать как реализацию схемы, показанной на рис. 2.25. Предположим, что последовательность двоичных символов ![]() необходимо передать на скорости R символов/с через систему, имеющую идеальный прямоугольный спектр ширины
необходимо передать на скорости R символов/с через систему, имеющую идеальный прямоугольный спектр ширины ![]() Гц. Вы можете спросить: чем этот квадратный спектр на рис. 2.25 отличается от нереализуемой характеристики Найквиста? Он имеет ту же идеальную характеристику, но дело в том, что мы не пытаемся реализовать идеальный прямоугольный фильтр. На рис. 2.25 изображена эквивалентная модель, используемая для разработки фильтра, который легче аппроксимировать. До подачи на идеальный фильтр импульсы, как показано на рисунке, проходят через простой цифровой фильтр. Цифровой фильтр вносит задержку, длительностью в одну цифру; к каждому поступающему импульсу фильтр добавляет значение предыдущего импульса. Другими словами, с выхода цифрового фильтра поступает сумма двух импульсов. Каждый импульс последовательности
Гц. Вы можете спросить: чем этот квадратный спектр на рис. 2.25 отличается от нереализуемой характеристики Найквиста? Он имеет ту же идеальную характеристику, но дело в том, что мы не пытаемся реализовать идеальный прямоугольный фильтр. На рис. 2.25 изображена эквивалентная модель, используемая для разработки фильтра, который легче аппроксимировать. До подачи на идеальный фильтр импульсы, как показано на рисунке, проходят через простой цифровой фильтр. Цифровой фильтр вносит задержку, длительностью в одну цифру; к каждому поступающему импульсу фильтр добавляет значение предыдущего импульса. Другими словами, с выхода цифрового фильтра поступает сумма двух импульсов. Каждый импульс последовательности ![]() , получаемой на выходе цифрового фильтра, можно выразить следующим образом.
, получаемой на выходе цифрового фильтра, можно выразить следующим образом.
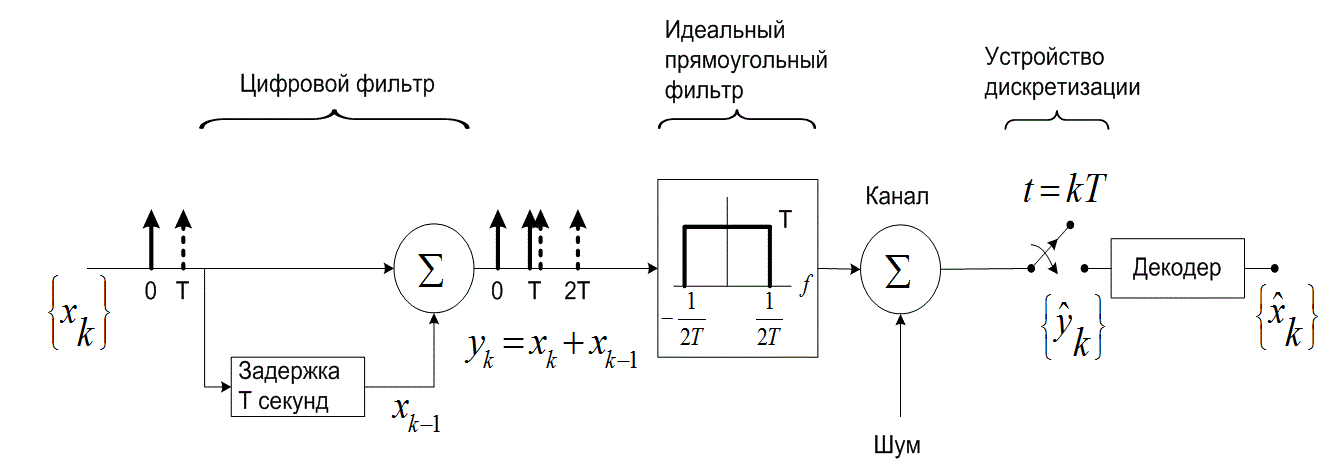
Рис. 2.25. Двубинарная передача сигналов
![]() (2.29)
(2.29)
Следовательно, амплитуды импульсов ![]() не являются независимыми; каждое значение
не являются независимыми; каждое значение ![]() использует предыдущее значение выходного сигнала. Межсимвольная интерференция, вносимая в каждую цифру
использует предыдущее значение выходного сигнала. Межсимвольная интерференция, вносимая в каждую цифру ![]() , проявляется только от предыдущей цифры
, проявляется только от предыдущей цифры ![]() . Эту корреляцию между амплитудами импульсов
. Эту корреляцию между амплитудами импульсов ![]() можно рассматривать как управляемую межсимвольную интерференцию, введенную двубинарным кодированием. Управляемая интерференция составляет суть этого нового метода, поскольку в детекторе она может удаляться так же легко, как была введена. Последовательность
можно рассматривать как управляемую межсимвольную интерференцию, введенную двубинарным кодированием. Управляемая интерференция составляет суть этого нового метода, поскольку в детекторе она может удаляться так же легко, как была введена. Последовательность ![]() проходит через идеальный фильтр Найквиста, который не вводит новой межсимвольной интерференции. В устройстве квантования приемника, показанном на рис. 2.25, мы надеемся (при отсутствии помех) точно восстановить последовательность
проходит через идеальный фильтр Найквиста, который не вводит новой межсимвольной интерференции. В устройстве квантования приемника, показанном на рис. 2.25, мы надеемся (при отсутствии помех) точно восстановить последовательность ![]() . Выходную последовательность
. Выходную последовательность ![]() , подверженную воздействию шума, обозначим через
, подверженную воздействию шума, обозначим через ![]() . Удаление управляемой интерференции с помощью двубинарного декодера дает восстановленную оценку
. Удаление управляемой интерференции с помощью двубинарного декодера дает восстановленную оценку ![]() , которую мы будем обозначать через
, которую мы будем обозначать через ![]() .
.
2.9.2. Двубинарное декодирование
Если двоичная цифра ![]() равна
равна ![]() , то, используя формулу (2.29), видим, что
, то, используя формулу (2.29), видим, что ![]() может принимать одно из трех значений: +2, 0 или -2. Двубинарный код дает трехуровневый выход: в общем случае, для М-уровневой кодировки передача сигналов с частичным откликом дает на выходе 2М- 1 уровней. Процедура декодирования включает процесс, обратный процедуре кодирования, который именуется вычитанием
может принимать одно из трех значений: +2, 0 или -2. Двубинарный код дает трехуровневый выход: в общем случае, для М-уровневой кодировки передача сигналов с частичным откликом дает на выходе 2М- 1 уровней. Процедура декодирования включает процесс, обратный процедуре кодирования, который именуется вычитанием ![]() решений из
решений из ![]() цифр. Рассмотрим следующий пример кодирования/декодирования.
цифр. Рассмотрим следующий пример кодирования/декодирования.
Пример 2.4. Двубинарное кодирование и декодирование
Воспользуемся формулой (2.29) для демонстрации двубинарного кодирования и декодирования следующей последовательности: ![]() . Первый бит последовательности будем считать начальной цифрой, а не частью информационной последовательности.
. Первый бит последовательности будем считать начальной цифрой, а не частью информационной последовательности.
Решение
Последовательность двоичных
цифр ![]() 0 0 1 0 1 1 0
0 0 1 0 1 1 0
Биполярные амплитуды ![]() -1 -1 +1 -1 +1 +1 -1
-1 -1 +1 -1 +1 +1 -1
Правило кодирования: ![]() -2 0 0 0 2 0
-2 0 0 0 2 0
Правило декодирования Если ![]() , то
, то ![]() (или двоичная единица)
(или двоичная единица)
Если ![]() , то
, то ![]() (или двоичный нуль) Если
(или двоичный нуль) Если ![]() , взять число, противоположное предыдущему
, взять число, противоположное предыдущему
Декодированная биполярная
последовательность ![]() -1 +1 -1 +1 +1 -1
-1 +1 -1 +1 +1 -1
Декодированная бинарная
последовательность ![]() 0 1 0 1 1 0
0 1 0 1 1 0
Правило принятия решения просто реализует вычитание каждого решения ![]() из каждого
из каждого ![]() . Одним из недостатков этого метода обнаружения является то, что при появлении ошибка имеет тенденцию к распространению, вызывая дальнейшие ошибки (причина в том, что текущее решение зависит от предыдущих). Избежать этого позволяет метод предварительного кодирования.
. Одним из недостатков этого метода обнаружения является то, что при появлении ошибка имеет тенденцию к распространению, вызывая дальнейшие ошибки (причина в том, что текущее решение зависит от предыдущих). Избежать этого позволяет метод предварительного кодирования.
2.9.3. Предварительное кодирование
Предварительное кодирование выполняется посредством первоначального дифференциального кодирования бинарной последовательности ![]() в новую бинарную последовательность
в новую бинарную последовательность ![]() , для чего используется выражение
, для чего используется выражение
![]()
где символ «![]() » представляет сложение двоичных цифр по модулю 2 (эквивалентно операции исключающего ИЛИ). Сложение по модулю 2 имеет следующие правила.
» представляет сложение двоичных цифр по модулю 2 (эквивалентно операции исключающего ИЛИ). Сложение по модулю 2 имеет следующие правила.
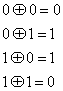
Затем двоичная последовательность ![]() преобразовывается в последовательность биполярных импульсов, и операция кодирования проходит так же, как было показано в примере 2.4. В то же время, как показано ниже, в примере 2.5 при выполнении предварительного кодирования процесс обнаружения отличается от обнаружения в обычной двубинарной схеме. Схема предварительного кодирования показана на рис. 2.26; стоит обратить внимание на то, что сложение по модулю 2, дающее предварительно кодированную последовательность
преобразовывается в последовательность биполярных импульсов, и операция кодирования проходит так же, как было показано в примере 2.4. В то же время, как показано ниже, в примере 2.5 при выполнении предварительного кодирования процесс обнаружения отличается от обнаружения в обычной двубинарной схеме. Схема предварительного кодирования показана на рис. 2.26; стоит обратить внимание на то, что сложение по модулю 2, дающее предварительно кодированную последовательность ![]() , выполняется над двоичными цифрами, а цифровая фильтрация, результатом которой является последовательность
, выполняется над двоичными цифрами, а цифровая фильтрация, результатом которой является последовательность ![]() , - над биполярными импульсами.
, - над биполярными импульсами.
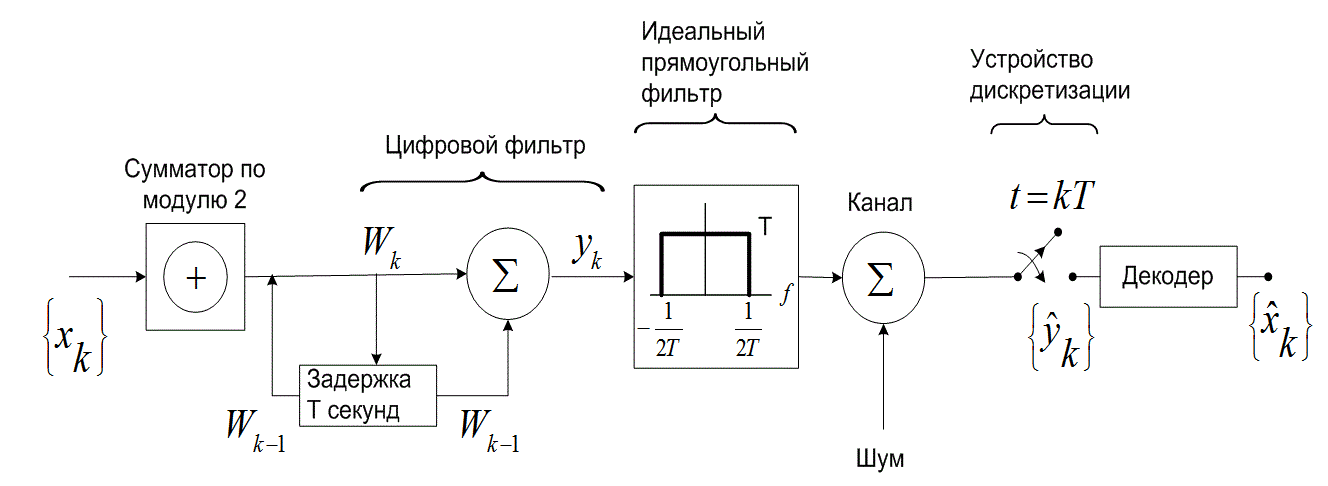
Рис.2.26. Передача сигналов с предварительным кодированием
Пример 2.5. Двубинарное предварительное кодирование
Проиллюстрируем правила двубинарного кодирования и декодирования при использовании предварительной дифференциальной кодировки, определенной формулой (2.30). Будем использовать ту же последовательность ![]() , что и в примере 2.4.
, что и в примере 2.4.
Решение
Последовательность двоичных
цифр ![]() 0 0 1 0 1 1 0
0 0 1 0 1 1 0
Предварительно кодированная
последовательность ![]() 0 0 1 1 0 1 1
0 0 1 1 0 1 1
Биполярная
последовательность ![]() -1 -1 +1 +1 -1 +1 +1
-1 -1 +1 +1 -1 +1 +1
Правило кодирования: ![]() -2 0 +2 0 0 +2
-2 0 +2 0 0 +2
Правило декодирования Если ![]() , то
, то ![]() двоичный нуль
двоичный нуль
Если ![]() , то
, то ![]() двоичная единица
двоичная единица
Декодированная бинарная
последовательность ![]() 0 1 0 1 1 0
0 1 0 1 1 0
Предварительное дифференциальное кодирование позволяет декодировать последовательность ![]() путем принятия решения по каждой принятой выборке отдельно, не обращаясь к предыдущим, которые могут быть ошибочными. Преимущество заключается в том, что при возникновении из-за помех ошибочной цифры ошибка не будет распространяться на другие цифры. Отметим, что первый бит двоичной последовательности
путем принятия решения по каждой принятой выборке отдельно, не обращаясь к предыдущим, которые могут быть ошибочными. Преимущество заключается в том, что при возникновении из-за помех ошибочной цифры ошибка не будет распространяться на другие цифры. Отметим, что первый бит двоичной последовательности ![]() , подвергаемой дифференциальному кодированию, выбирается произвольно. Если бы начальный бит последовательности
, подвергаемой дифференциальному кодированию, выбирается произвольно. Если бы начальный бит последовательности ![]() был выбран равным 1, а не 0, результат декодирования был бы таким же.
был выбран равным 1, а не 0, результат декодирования был бы таким же.
2.9.4. Эквивалентная двубинарная передаточная функция
В разделе 2.9.1 двубинарная передаточная функция реализовывалась как цифровой фильтр, вводящий задержку длительностью в одну цифру, за которым следовала идеальная прямоугольная передаточная функция. Рассмотрим эквивалентную модель. Фурье-образ задержки можно записать как ![]() (см. раздел А.3.1); следовательно, первый цифровой фильтр на рис. 2.25 можно описать следующей частотной характеристикой.
(см. раздел А.3.1); следовательно, первый цифровой фильтр на рис. 2.25 можно описать следующей частотной характеристикой.
![]() (2.31)
(2.31)
Передаточная функция идеального прямоугольного фильтра имеет следующий вид.
![]()
![]()
![]()
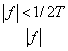 (2.32)
(2.32)
Таким образом, общая эквивалентная передаточная функция цифрового и идеального прямоугольного фильтров дается выражением
![]() при
при ![]()
![]() , (2.33)
, (2.33)
так что
![]()
![]()
![]()
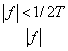 (2.34)
(2.34)
Таким образом, ![]() , составная передаточная функция последовательности цифрового и прямоугольного фильтров, последовательно выравнивает край полосы пропускания, как показано на рис. 2.27, а. Передаточную функцию можно аппроксимировать, используя для этого реализуемый аналоговый фильтр; отдельный цифровой фильтр не нужен. Двубинарный эквивалент
, составная передаточная функция последовательности цифрового и прямоугольного фильтров, последовательно выравнивает край полосы пропускания, как показано на рис. 2.27, а. Передаточную функцию можно аппроксимировать, используя для этого реализуемый аналоговый фильтр; отдельный цифровой фильтр не нужен. Двубинарный эквивалент ![]() называется косинусоидальным фильтром [8]. Этот фильтр не следует путать с фильтром с характеристикой типа приподнятого косинуса (описанным в главе 3, раздел 3.3.1.) Соответствующая импульсная характеристика
называется косинусоидальным фильтром [8]. Этот фильтр не следует путать с фильтром с характеристикой типа приподнятого косинуса (описанным в главе 3, раздел 3.3.1.) Соответствующая импульсная характеристика ![]() получается, если взять Фурье-образ функции
получается, если взять Фурье-образ функции ![]() , описанной в формуле (2.33).
, описанной в формуле (2.33).
![]() (2.35)
(2.35)
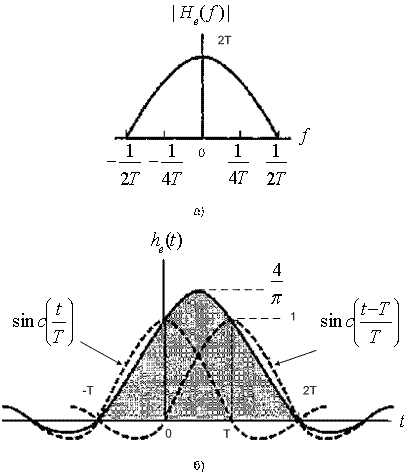
Рис.2.27. Двубинарная передаточная функция и форма импульса: а) косинусоидальный фильтр; б) импульсная характеристика
косинусоидального фильтра
Эта функция изображена на рис. 2.27, б. Для импульса ![]() , поданного на вход схемы, изображенной на рис. 2.25, на выход поступит сигнал
, поданного на вход схемы, изображенной на рис. 2.25, на выход поступит сигнал ![]() соответствующей полярности. Отметим, что в каждом Т-секундном интервале имеется всего две ненулевые выборки, которые вносят вклад в управляемую межсимвольную интерференцию с соседними битами. Внесенная межсимвольная интерференция устраняется путем использования процедуры декодирования, описанной в разделе 2.9.2. Хотя косинусоидальный фильтр не является причинным, а следовательно нереализуем, его можно легко аппроксимировать. Реализацию двубинарного метода с предварительным кодированием, описанного в разделе 2.9.3, можно выполнить следующим образом. Вначале двоичная последовательность
соответствующей полярности. Отметим, что в каждом Т-секундном интервале имеется всего две ненулевые выборки, которые вносят вклад в управляемую межсимвольную интерференцию с соседними битами. Внесенная межсимвольная интерференция устраняется путем использования процедуры декодирования, описанной в разделе 2.9.2. Хотя косинусоидальный фильтр не является причинным, а следовательно нереализуем, его можно легко аппроксимировать. Реализацию двубинарного метода с предварительным кодированием, описанного в разделе 2.9.3, можно выполнить следующим образом. Вначале двоичная последовательность ![]() с использованием дифференциального кодирования превращается в последовательность
с использованием дифференциального кодирования превращается в последовательность ![]() (см. пример 2.5). Затем последовательность импульсов
(см. пример 2.5). Затем последовательность импульсов ![]() фильтруется схемой с эквивалентной косинусоидальной характеристикой, описанной в формуле (2.34).
фильтруется схемой с эквивалентной косинусоидальной характеристикой, описанной в формуле (2.34).
2.9.5. Сравнение бинарного и двубинарного методов передачи сигналов
Двубинарный метод вводит корреляцию между амплитудами импульсов, тогда как критерий Найквиста предполагает независимость амплитуд передаваемых импульсов. Выше показывалось, что двубинарная передача сигналов может использовать введенную корреляцию для получения передачи без межсимвольной интерференции, требуя при этом меньшую полосу, чем пришлось бы использовать в ином случае. Можно ли получить это преимущество без сопутствующих недостатков? К сожалению, нет. Практически всегда при принятии конструкторского решения требуется искать приемлемый компромисс. Выше демонстрировалось, что двубинарное кодирование требует трех уровней, а не двух, как при обычном бинарном кодировании. Вспомним раздел 2.8.5, где мы сравнивали производительность и требуемую мощность сигнала при выборе между восьмиуровневой кодировкой РАМ и двухуровневой РСМ, При фиксированной мощности сигнала принятие правильного решения обратно пропорционально числу уровней сигнала, которые необходимо различать. Следовательно, не должно удивлять то, что, хотя двубинарная передача сигналов позволяет получить нулевую межсимвольную интерференцию при минимальной ширине полосы, такая схема требует большей мощности, чем бинарная передача сигналов для получения равносильного сопротивления шуму. Для данной вероятности появления ошибочного бита ![]() двубинарная схема передачи сигналов требует приблизительно на 2,5 дБ большего отношения сигнал/шум, чем бинарная схема, используя при этом всего лишь
двубинарная схема передачи сигналов требует приблизительно на 2,5 дБ большего отношения сигнал/шум, чем бинарная схема, используя при этом всего лишь ![]() полосы, требуемой бинарной схемой [7], где
полосы, требуемой бинарной схемой [7], где ![]() - сглаживание фильтра.
- сглаживание фильтра.
2.9.6. Полибинарная передача сигналов
Двубинарная передача сигналов может быть расширена на большее, чем три, количество уровней, что приводит к большей эффективности использования полосы; называются подобные системы полибинарными [7, 9]. Предположим, что бинарное сообщение с двумя сигнальными уровнями преобразовывается в сигнал с ![]() уровнями, последовательно пронумерованными от нуля до
уровнями, последовательно пронумерованными от нуля до ![]() . Преобразование двубинарного сигнала в полибинарный проходит в два этапа. Вначале исходная последовательность
. Преобразование двубинарного сигнала в полибинарный проходит в два этапа. Вначале исходная последовательность ![]() , состоящая из двоичных нулей и единиц, преобразовывается в другую бинарную последовательность
, состоящая из двоичных нулей и единиц, преобразовывается в другую бинарную последовательность ![]() . Текущее двоичное число последовательности
. Текущее двоичное число последовательности ![]() формируется путем сложения по модулю 2
формируется путем сложения по модулю 2 ![]() непосредственно предшествующих цифр последовательности
непосредственно предшествующих цифр последовательности ![]() и текущего числа
и текущего числа ![]() . Например, пусть
. Например, пусть
![]() , (2.36)
, (2.36)
где ![]() представляет входящие двоичные цифры, a
представляет входящие двоичные цифры, a ![]() -
- ![]() -ю кодируемую цифру. Поскольку выражение включает
-ю кодируемую цифру. Поскольку выражение включает ![]() бит, предшествующих
бит, предшествующих ![]() , имеем
, имеем ![]() сигнальных уровней. Далее двоичная последовательность
сигнальных уровней. Далее двоичная последовательность ![]() преобразовывается в серию полибинарных импульсов
преобразовывается в серию полибинарных импульсов ![]() , для чего текущий бит последовательности
, для чего текущий бит последовательности ![]() алгебраически складывается с
алгебраически складывается с ![]() предыдущими битами последовательности
предыдущими битами последовательности ![]() . Следовательно,
. Следовательно, ![]() по модулю 2 равно
по модулю 2 равно ![]() , и двоичные элементы один и нуль отображаются в импульсы с четными и нечетными значениями последовательности
, и двоичные элементы один и нуль отображаются в импульсы с четными и нечетными значениями последовательности ![]() . Отметим, что каждая цифра
. Отметим, что каждая цифра ![]() может обнаруживаться независимо, несмотря на сильную корреляцию между битами. Главным преимуществом подобной схемы передачи сигналов является перераспределение спектральной плотности исходной последовательности
может обнаруживаться независимо, несмотря на сильную корреляцию между битами. Главным преимуществом подобной схемы передачи сигналов является перераспределение спектральной плотности исходной последовательности ![]() в пользу низких частот, что, в свою очередь, повышает эффективность использования системы.
в пользу низких частот, что, в свою очередь, повышает эффективность использования системы.

