Передаточная функция цепи по напряжению

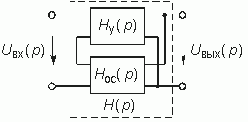
Определим передаточную функцию по напряжению цепи с обратной связью на примере схемы, изображенной на рис. 14.1 а, и проанализируем влияние ОС на основные параметры усилителя с ОС цепи как сложного четырехполюсника.

Для этого типа ОС можно записать следующее равенство согласно ЗНК в операторной форме (рис. 14.1, а):

Тогда для изображения выходного напряжения можно согласно рис. 14.2 записать:

где – операторная передаточная функция по напряжению.

Операторное изображение U_ос(р) можно записать через передаточную функцию Н_ос(р) цепи обратной связи

а напряжение U₁(р) через передаточную функцию усилителя Н_у(р):

Отсюда с учетом (14.1) и (14.2) операторная передаточная функция по напряжению цепи с ОС (см. рис. 14.2) будет равна

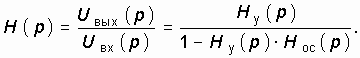
Переходя в (14.3) от оператора р к оператору jw , получаем комплексную передаточную функцию

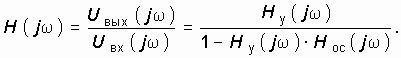
Таким образом, частотные свойства цепи в равной мере зависят как от H_у(jw ) канала прямого усиления, так и от Н_ос(jw ) цепи обратной связи. Поэтому можно, оставляя неизменным основной элемент системы, в широких пределах изменять частотную характеристику всей цепи, изменяя лишь параметры цепи обратной связи.

Произведение H_у(jw )× Н_ос(jw ) = Н_р(jw ) представляет собой комплексную передаточную функцию усилителя и цепи обратной связи при условии, что обратная связь разорвана (рис. 14.3, а). Функцию Н_р(jw ) называют передаточной функцией по петле ОС или петлевым усилением. Введем понятия положительной и отрицательной обратной связи. Эти понятия играют заметную роль в теории цепей с обратной связью.

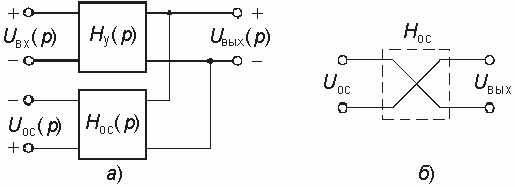
Предположим вначале, что передаточные функции H_у, Н_ос, Н_р не зависят от частоты и являются вещественными числами. Такая ситуация возможна, когда в цепи отсутствуют LC-элементы. При этом Н_р может быть как положительным, так и отрицательным числом. В первом случае сдвиг фаз между входным и выходным напряжениями, или другими словами, сдвиг фаз по петле обратной связи равен нулю или 2kp , k = 0, 1, 2, ... Во втором случае, когда Н_р < 0, сдвиг фаз по этой петле равен ±p или ±(2k – 1)p . (Заметим, что сдвиг фаз на ±p можно легко получить путем перекрещивания проводов, например так, как показано на рис. 14.3, б).

Если в цепи с обратной связью сдвиг фаз по петле равен нулю, то обратная связь называется положительной, если же сдвиг фаз равен ±p , то такая обратная связь называется отрицательной.

Передаточную функцию Н_р(jw ) можно изобразить в виде векторов и показать их на комплексной плоскости. При положительной обратной связи вектор Н_р(jw ) находится на положительной вещественной полуоси, а при отрицательной обратной связи — на отрицательной вещественной полуоси.

Напомним, что годографом называется кривая, которую описывает конец вектора Н_р(jw ) при изменении частоты w (рис. 4.3, в и 14.4).

Представление Н_р(jw ) в виде годографа позволяет определить вид обратной связи в случае частотнозависимой обратной связи.

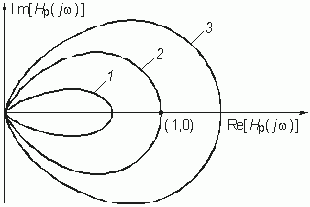
Обратная связь называется положительной, если годограф Н_р(jw ) лежит в правой, и отрицательной – если в левой полуплоскости комплексной плоскости. Отрицательная ОС применяется для стабилизации коэффициента усиления, подавления паразитных сигналов, коррекции частотных характеристик; положительная ОС может являться причиной неустойчивости цепи. Поясним это. Пусть Н_ос и H_у – положительные вещественные числа. Тогда при H_у× Н_ос = 1, т. е. когда Н_ос = 1/ H_у, значение передаточной функции (14.4) стремится к бесконечности. Это означает, что даже при бесконечно малых значениях амплитуды входного напряжения u_вx(t) амплитуда выходного напряжения u_выx(t) будет неограниченно возрастать. Говорят, что в этом случае наступает самовозбуждение цепи с ОС. Поэтому при проектировании цепей с обратной связью одной из основных задач является исследование их устойчивости. Таким образом, термины неустойчивость и самовозбуждение являются синонимами.

Влияние ОС на параметры усилителя

Обратная связь существенно влияет на результирующие параметры цепи с ОС; в частности ее входное и выходное сопротивления и коэффициенты передачи. Рассмотрим влияние ОС на параметры усилителя на примере схемы, изображенной на рис. 14.2.

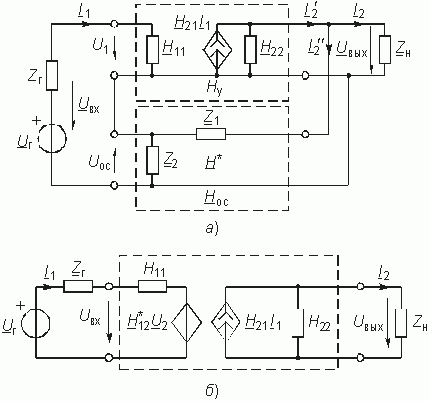
На рис. 14.5 изображена эквивалентная схема с зависимым источником напряжения с H-параметрами при отсутствии внутренней ОС (H₁₂ = 0);

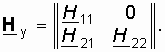
Четырехполюсник ОС представлен в виде четырехполюсника с матрицей H_ос-параметров

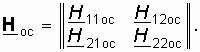
Запишем согласно (12.5) уравнения активного и пассивного четырехполюсников в H-параметрах:

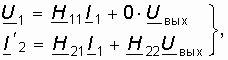
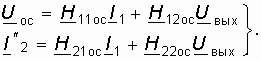
Матрица H-параметров сложного четырехполюсника определяется с учетом 12.3. Применение матриц к расчету четырехполюсников как

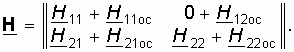
Поскольку в данной схеме (рис. 14.5) ОС предназначена для получения на выходе четырехполюсника определенного напряжения U_ос, то основное значение на свойство усилителя должен играть коэффициент H_12ос. Учитывая, что цепь ОС отбирает часть полезной энергии из нагрузки необходимо стремиться, чтобы H_22ос H₂₂. Кроме того, для уменьшения потерь входного сигнала на входном сопротивлении цепи с ОС, необходимо выполнение условия H₁₁ H_11ос. Если при этом учесть, что обычно H₂₁ H_21ос и для пассивной цепи H_12ос < 1, то окончательно матрица H-параметров сложного четырехполюсника с цепью ОС примет вид

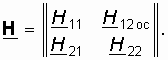
При этом уравнения передачи H-параметров примут вид (рис. 14.5, б)

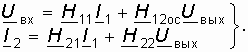
С помощью системы уравнений (14.9) можно определить искомые зависимости токов и напряжений от параметров цепи ОС. Можно, в частности показать, что отрицательная ОС (ООС) уменьшает коэффициент передачи по напряжению усилителя в k-раз, а входное сопротивление увеличивает в k-раз, где

Так как рассмотренный тип ОС (последовательной по напряжению) ведет к увеличению входного и уменьшению выходного сопротивлений усилителя, то это позволяет осуществить трансформацию сопротивлений, что используется для согласования отдельных каскадов усилителя.

Следует также отметить, что коэффициент передачи ОУ с последовательной ОС по напряжению при бесконечно большом коэффициенте усиления является функцией только параметров элементов цепи ОС.

В заключении рассмотрим влияние ОС на стабильность коэффициента усиления, как основного показателя усилителя.

Для отрицательной и вещественной ОС согласно уравнению (14.4) для коэффициента усиления усилителя можно записать

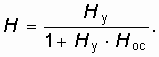
Продифференцируем (14.11) по H_у и H_ос

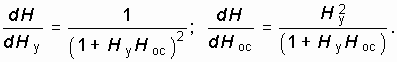
Отсюда относительная нестабильность коэффициента усиления с учетом (14.11) будет равна

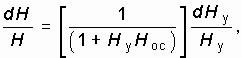
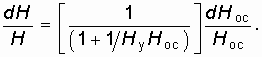
Анализ (14.13) показывает, что нестабильность коэффициента усиления усилителя с ОС в раз меньше чем без ОС.

Равенство (14.14) показывает, что при , т. е. пропорционально нестабильности коэффициента передачи цепи ОС, поэтому стараются цепь ОС сделать достаточно стабильной.

Аналогичным образом можно найти коэффициент передачи и исследовать влияние ОС на параметры других схем с ОС (см. рис. 14.1 б)—г)). При этом надо иметь ввиду, что в соответствующих выражениях будут фигурировать не только комплексные коэффициенты передачи по напряжению, но и по току, а также передаточные комплексные сопротивления и проводимости. Кроме того уравнения передачи соответствующих четырехполюсников в зависимости от типа соединения должны быть записаны в Z или F-параметрах.