4.1. Общие сведения о приеме сигналов
4.3. Когерентный и некогерентный приемы
4.6. Прием на согласованный фильтр
4.1. Общие сведения о приеме сигналов
На приемной стороне о передаваемых сигналах обычно имеются некоторые предварительные (априорные) сведения. Могут быть известными, например, частота несущей, вид модуляции и т. п. Сигнал, о котором заранее все известно, не несет информации, а абсолютно неизвестный сигнал нельзя было бы принять.
Известные параметры сигнала используются в приемнике для лучшего отделения сигналов от помех. Чем больше мы знаем о сигнале, тем совершеннее могут быть методы приема.
Параметры, в изменениях которых заложена переносимая сигналом информация, называются информационными. Изменения этих параметров на приемной стороне заранее неизвестны.
В зависимости от вида и назначения передачи при приеме сигналов возникают следующие основные задачи: 1) обнаружение сигналов, 2) различение сигналов и 3) восстановление сигналов.
При обнаружении сигналов задача сводится к получению ответа на вопрос, имеется на входе приемника сигнал или нет, точнее, имеется ли на входе сигнал плюс шум или только шум. С такой задачей мы обычно встречаемся в радиолокации, она также имеет место и в некоторых системах связи. Если мы в состоянии обнаружить сигнал, то появляется возможность передачи информации при помощи двоичного кода. Наличие сигнала (посылка) будет соответствовать символу 1, отсутствие сигнала (пауза) — символу 0. Этот принцип используется в системах с пассивной паузой.
При передаче двух сигналов s1 и s2 возникает задача не обнаружения, а различения сигналов. Здесь необходимо дать ответ на вопрос: имеется ли на входе приемника сигнал s1 или сигнал s2. Ответ на этот вопрос определяется уже не свойствами каждого сигнала в отдельности, а их различием. Сигналы могут отличаться один от другого своими параметрами. Очевидно, нужно стремиться к тому, чтобы различие было наибольшим и устойчивым к воздействию помех. Случай обнаружения может рассматриваться как вырожденный случай различения двух сигналов, когда один из них тождественно равен нулю.
Передача двоичным кодом, в котором каждому символу (1 и О) соответствует определенный сигнал (s1 и s2), не равный нулю, называется передачей с активной паузой. Случай различения многих сигналов принципиально мало отличается от случая различения двух сигналов.
Задача восстановления сообщения существенно отличается от задач обнаружения и различения сигналов. Она состоит в том, чтобы получить выходной видеосигнал v(t), наименее отличающийся от переданного сообщения u(t). При этом сообщение u(t) заранее неизвестно; известно лишь, что оно принадлежит к некоторому множеству или является реализацией некоторого случайного процесса.
На рис. 4.1 приведена функциональная схема обработки дискретных/сигналов. Принятый сигнал, искаженный помехой, в приемнике подвергается определенной обработке, детектируется и поступает для опознавания на решающее устройство.
Рис. 4.1. Функциональная схема обработки дискретных сигналов
Очевидно, что вероятность правильного опознавания сигналов существенно зависит от отношения сигнала к помехе на входе решающего устройства. В связи с этим основной задачей обработки сигналов в приемнике является увеличение отношения сигнал/шум. Обработка сигналов, как правило, сводится к тем • или иным методам фильтрации.
В каскадах обработки производится также усиление сигналов до величин, при которых могут нормально работать детектор и решающее устройство.
В обычном приемнике непрерывных сигналов додетекторная обработка сигналов осуществляется с помощью резонансных усилителей, обеспечивающих необходимую частотную селекцию. Функции последетекторной обработки при этом выполняются видеоусилителем (или усилителем низкой частоты). Решающее устройстве в таких приемниках отсутствует. Вместо него на выходе имеется устройство, воспроизводящее или записывающее (регистрирующее) принятое сообщение.
В системах передачи дискретных сообщений основными видами обработки сигналов в приемнике являются фильтрация со стробированием, интегрирование и корреляционная обработка.
Стробирование сигнала является простейшим видом обработки Оно давно известно и широко применяется в практике. Обработку сигналов стробированием часто называют приемом по методу укороченных контактов. При стробировании данного элемента сигнала производится отсчет его текущего значения (напряжения или тока) в определенный момент времени. Последний выбирается в той части элемента, которая в наименьшей степени подвержена искажениям. Так как статистические характеристики помех мало зависят от выбора момента времени, то момент стробирования необходимо выбирать тогда, когда полезный сигнал имеет максимальное значение. Вследствие переходных процессов в фильтрах границы элементов сигнала в значительной степени искажены и поэтому максимальное значение сигнала, как правило, соответствует средней части элемента. Стробирование производится при помощи специальных сигналов, поступающих от системы синхронизации.
Фильтрация принимаемых сигналов может выполняться как до, так и после детектора. При использовании синхронного детектора фильтрация до и после детектора принципиально может дать один я тот же результат. Практически же обычно производят фильтрацию сигнала дважды: как до, так и после детектора.
Операция интегрирования может рассматриваться либо как процесс накопления (суммирования), либо как определение среднего значения сигнала. Любой фильтр в той или иной мере производит интегрирование поступающего на его вход колебания. При определенных условиях операция интегрирования эквивалентна фильтрации. Интегрирование, так же как и фильтрация, может осуществляться либо до, либо после детектора.
Методы приема можно классифицировать по видам применяемых детекторов, по способам додетекторной и последетекторной обработки. Различают следующие основные методы приема: 1) когерентный, 2) некогерентный, 3) корреляционный и 4) автокорреляционный.
4.2. Методы накопления
Одним из эффективных и широко применяемых в различных вариантах методов борьбы с помехами является метод накопления. Сущность метода состоит в том, что сигнал или его элементы многократно повторяются. На приеме отдельные образцы сигнала сличаются (обычно суммируются), и так как различные образцы по-разному искажаются помехой в силу независимости последних, то можно восстановить переданный сигнал с большей достоверностью.
В простейшей форме метод накопления часто применяется при телефонном разговоре в условиях плохой слышимости, когда переспрашивают и повторяют одно и то же слово по нескольку раз.
В случае телеграфной связи каждая кодовая комбинация, состоящая из элементов 0 и 1, передается несколько раз. Если вероятность сбоя символов 1 и 0 одинакова, то на приеме решение выносится «по большинству», т. е. воспроизводится символ 1 на данной позиции, когда их число на этой позиции больше числа символов 0, и, наоборот, воспроизводится 0, когда число «нулей» больше числа «единиц»:
переданная комбинация 01001
первая принятая 00001
вторая 11010
третья 01101
воспроизведенная комбинация 01001
Заметим, что можно было бы получить п образцов сигнала не путем их повторения во времени, а путем передачи по независимым каналам, разделенным по частоте, или каким-либо другим способом.
Существуют и другие разновидности метода накопления. К ним, в частности, относится метод синхронного накопления, нашедший применение в радиолокации. При этом методе на протяжении посылки сигнала берется не один отсчет, а несколько. На приеме эти отсчеты суммируются в накопителе.
Пусть отдельные отсчеты принятого сигнала:
,
,…
(4.1)
тогда сумма отсчетов
(4.2)
Величина b = ns представляет собой полезный сигнал на выходе
приемника. Случайная величина 
представляет собой помеху. Отношение сигнала к помехе на выходе приемника 
равно: 
(4.3)
Здесь мы полагали, что 
некоррелированы и имеют одинаковое распределение, 
отношение сигнала к помехе на входе приемника.
Таким образом, при описанных условиях накопление отсчетов сигнала позволяет увеличить отношение сигнала к помехе на выходе приемника ровно в п раз. Суть дела сводится к тому, что мощность сигнала при суммировании растет пропорционально п2 (складываются напряжения), а мощность помехи — пропорционально п (суммируются мощности). Поэтому отношение сигнала к помехе увеличивается в п раз, если помехи независимы. При наличии корреляции между значениями помехи этот выигрыш будет меньше.
Метод накопления можно осуществить, беря не сумму отсчетов xk, а интеграл непрерывно изменяющейся функции x(t)=s+
(t) за время Т, равное длительности сигнала,
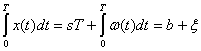
Здесь b — также постоянная, выражающая сигнал на выходе накопителя (интегратора), а |
— случайная величина, определяющая помеху на выходе интегратора.
Определим дисперсию случайной величины
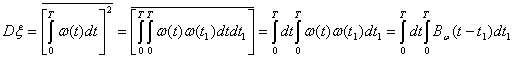(4.4.)
где 
— функция корреляции помехи 
. Если спектр помехи равномерен в достаточно широкой полосе частот F, т. е. интервал корреляции помехи 
, то конечные пределы интегрирования могут быть заменены на бесконечные:
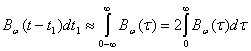(4.5)
где 
. По определению (2.24) интервал корреляции
(4.6)
В рассматриваемом случае 
и 
. Следовательно, 
Тогда отношение сигнала к помехе на выходе интегратора будет
(4.7)
Итак, выигрыш, получаемый при интегрировании, тем больше, чем больше отношение 
. Описанный способ приема называется интегральным.
Заметим, что 
есть число независимых отсчетов помехи на интервале Т. Это означает, что ф-лы (4.3) и (4.7) совпадают, т. е. замена суммирования независимых значений непрерывным интегрированием дополнительного выигрыша не дает. Однако практическая реализация метода интегрирования осуществляется проще, чем суммирование дискретных значений. Так, при приеме телеграфных сигналов в качестве интегратора широко используется цепочка RC, разряжаемая синхронно по окончании каждой элементарной посылки (рис. 4.2). В конце каждой посылки заряд на емкости приблизительно пропорционален интегралу входного сигнала. Додетекторное интегрирование можно осуществить с помощью резонатора большой добротности.
В простейшем случае таким резонатором может быть колебательный контур.
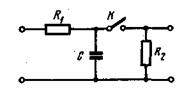
Рис. 4.2. Простейшая схема интегратора
4.3. Когерентный и некогерентный приемы
Функциональная схема когерентного приемника приведена на рис. 4.3. Она состоит из перемножителя П, генератора опорного колебания Г и фильтра нижних частот ФНЧ. Опорное колебание s0(t) при когерентном приеме представляют собой точную копию переданного сигнала s(t). Если сигналом s(t) является колебание с известной частотой и фазой, то в приемнике используется синхронный детектор, в котором опорное колебание синхронно с колебанием несущей частоты. Фильтр нижних частот выполняет роль интегратора, он выделяет на выходе напряжение, практически совпадающее с огибающей входного (высокочастотного) сигнала.
Рис. 4.3. Структурная схема когерентного приемника
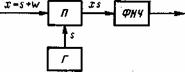Рис. 4.3. Структурная схема некогерентного приемника
При некогерентном приеме априорные сведения о начальной фазе принятого сигнала не учитываются, поэтому в схеме приемника можно применить не синхронный, а амплитудный детектор (рис. 4.4). Пусть на приемник воздействует регулярный сигнал
(4.8)
и флуктуационная помеха (t) . Помеху с симметричным относительно частоты сигнала спектром можно записать в виде квазигармонического колебания (2.37).
(4.9)
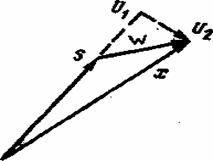
Рис. 4.5. Векторная диаграмма сигнала и помехи
где U
и U2 — случайные независимые величины, имеющие нормальное распределение вероятностей со средним значением, равным нулю, и дисперсией 
, где N0 — спектральная плотность помехи, F — эффективная ширина спектра помехи. Суммарное колебание сигнала и помехи.
(4.10)
В соответствии с этим выражением на рис. 4.5 построена векторная диаграмма сигнала и помехи. Согласно этой диаграмме помеха представляется относительно сигнала в виде двух находящихся в квадратуре составляющих: U и U2.
При когерентном приеме детектор выделяет сигнал и синфазную составляющую помехи U. Квадратурная составляющая помехи U
при этом полностью исключается. Ошибки при когерентном приеме обусловлены флуктуациями амплитуды помехи U, имеющей нормальное распределение вероятностей (2.28)
При некогерентном приеме детектор peaгирует на обе составляющие U и U выделяет огибающую суммарного колебания сигнала и помехи х. Ошибки в этом случае обусловлены флуктуациями огибающей U суммарного колебания x(t), которая распределена по обобщенному закону Рэлея (2.48).
При некогерентном приеме используются различные типы детекторов, которые принято классифицировать по виду их характеристик: линейный детектор, квадратичный и т. п.
Рассмотрим воздействие синусоидального сигнала и узкополосного нормального шума на амплитудный детектор и определим отношение сигнала к шуму на его выходе. Указанная задача решается при помощи хорошо разработанного корреляционного метода. Этот метод является достаточно общим и сводится к следующему. Для заданной характеристики детектора y=f(x) определяется среднее значение у (тока или напряжения):
(4.11)
Для получения постоянной составляющей выходного колебания необходимо 
усреднить еще по времени:
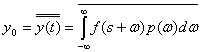(4.12)
Флуктуационная составляющая на выходе детектора определяется разностью 
, а регулярная переменная составляющая 
. Под сигналом обычно понимается низкочастотная составляющая величины b или приращение величины у
при подаче навход сигнала. Таким образом, колебание на выходе детектора можно представить в виде суммы
(4.13)
Первое слагаемое представляет собой постоянную составляющую, второе — регулярную составляющую (сигнал) и третье — помеху на выходе детектора. Превышение сигнала над помехой можно определить как отношение bгк дисперсии помехи D
(4.14)
Пусть характеристика детектора является квадратичной у=х2. На детектор воздействуют сигнал (4.8) и помеха (4.9) . Тогда колебание на выходе детектора будет
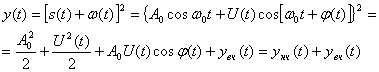
Высокочастотные составляющие увчотфильтровываются и поэтому могут не приниматься во внимание. На выходе фильтра нижних частот имеем колебание
(4.15)
Первое слагаемое 
определяет сигнал, второе и третье 
— помеху на выходе. Определим дисперсию шума на выходе детектора
(4.16)
Здесь учтено, что 
и 
Отношение сигнала к помехе на выходе квадратичного детектора
(4.17)
где 
отношение сигнала к помехе на входе детектора.
При значениях q
>>1
(4.18)
а при малых значениях q<<1,
(4.19)
зависимость квадратичная. Превышение сигнала над помехой в этой области резко уменьшается с уменьшением qвх. Здесь имеет место подавление слабого сигнала помехой. Так, при qвх.=0,1 отношение qвых.
0б01— подавление в десять раз.
Аналогично решается задача для линейного и других видов детекторов. Не останавливаясь на их анализе, отметим, что при слабых сигналах любой амплитудный детектор (кроме синхронного) является квадратичным.
При когерентном (синхронном) детектировании опорное колебание s0(t) выбирается подобным ожидаемому сигналу:
(4.20)
На выходе детектора получаем произведение двух колебаний
В соответствии с (4.8), (4.9) и (4.20) имеем
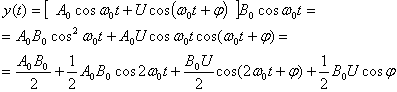
Отсюда
(4,21)
где
Дисперсия шума на выходе
Превышение сигнала над помехой на выходе синхронного детектора
(4.22)
Полученное соотношение показывает, что при когерентном детектировании отношение сигнала к помехе на выходе линейно зависит от отношения сигнала к помехе на входе. Явление подавления сигнала помехой отсутствует. Линейные свойства когерентного приемника определяют его высокие показатели в отношении помехоустойчивости. Преимущества когерентного детектора по сравнению с амплитудным особенно заметно при малых значениях 
Так, если 
, то при квадратичном детектировании 
, а при синхронном детектировании 
. Выигрыш 
Хотя приведенное выше рассмотрение относится к гармоническому сигналу, полученные выводы могут быть полностью распространены и на модулированные (манипулированные) сигналы.
4.4. Корреляционный прием
Структурная схема корреляционного приемника приведена на рис. 4.6. Она состоит из перемножителя П, генератора опорного колебания Г и интегратора И.
При корреляционном приеме в некоторый момент времени Т измеряется значение функции взаимной корреляции у(Т) принятого сигнала x(t)=s(t)+w(t) и опорного колебания s(t). Если спорное колебание тождественно переданному сигналу, т. е. s0(t)=s(t), то эту функцию можно записать в следующем виде:
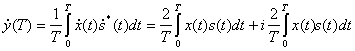(4.23)
где 
и 
— аналитические сигналы, соответствующие x(t) и s(i); s*(t) — функция комплексно-сопряженная с сигналом s(t).
В зависимости от метода регистрации сигнала на выходе корреляционный прием может быть когерентным и некогерентным.
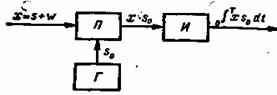
Рис. 4.6. Структурная схема корреляционного приемника
При когерентном приеме в момент времени Т отсчитывается действительное значение функции уТ, т. е.
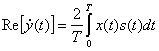(4.24)
При некогерентном приеме отсчитывается модуль этой функции
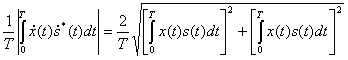(4.25)
Действительное значение сигнала на выходе корреляционного приемника можно представить в виде суммы двух составляющих
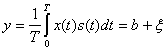
где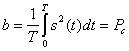 
— полезный сигнал, 
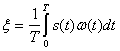помеха на выходе приемника. Определим дисперсию помехи
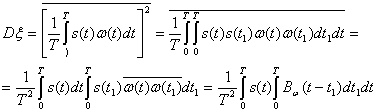(4.26)
Предположим, что интервал корреляции помехи 
настолько мал, что сигнал в течение этого интервала практически не изменяется (ширина спектра сигнала мала по сравнению с шириной спектра помехи). Тогда с учетом соотношений (4.5) и (4.6) получим
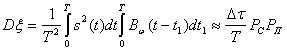(4.27)
где PП—Bw(0) — мощность помехи на входе приемника.
Отношение сигнала к помехе на выходе корреляционного приемника при когерентном приеме будет равно:
(4.28)
При некогерентном приеме это отношение будет в два раза меньше:
(4.29)
Сравнение ф-л (4.7) и (4.28) показывает, что корреляционный способ приема можно рассматривать как обобщение метода накопления на сигналы произвольной формы.
4.5. Автокорреляционный прием
В схеме автокорреляционного приемника отсутствует специальный генератор опорных колебаний (рис. 4.7). Зато в ней имеется линия задержки ЛЗ, осуществляющая задержку принимаемого сигнала на время т. Задержанное колебание 
используется в качестве опорного.
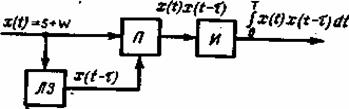
Рис. 4.7. Структурная схема автокорреляционного приемника
В случае автокорреляцион-ного приема выполняется интегральная операция
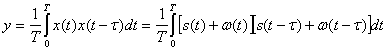(4.30)
Раскрывая скобки и полагая 
, получим
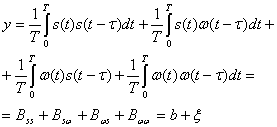(4.31)
Здесь:
Далее можно показать, что отношение сигнала к помехе на выходе автокорреляционного приемника при малом уровне помех (q>>1) будет примерно таким же, как и для корреляционного приемника. При большом уровне помех (q<<1) автокорреляционный приемник по помехоустойчивости приближается к приемнику с квадратичным детектором. Более низкая помехоустойчивость автокорреляционного приемника по сравнению с корреляционным при любых значениях q обусловлена наличием помехи в тракте опорного напряжения. Автокорреляционный прием возможен и в том случае, когда отсутствуют сведения не только о фазе сигнала, но и о частоте. Это возможно благодаря тому, что опорное колебание порождается самим принимаемым сигналом, а не создается специальным генератором в месте приема.
Для примера рассмотрим автокорреляционный прием периодического сигнала на фоне аддитивной флуктуационной помехи. Пусть s(t) — периодический сигнал, a (t) — помеха, которую будем считать эргодическим процессом. Суммарное колебание сигнала и помехи на входе приемника x(t)=s(t) + w(t). Определим функцию корреляции этого колебания
. Так как сигнал и помеху можно считать независимыми, то их взаимно корреляционные функции Bsw и Bws обращаются в нуль.
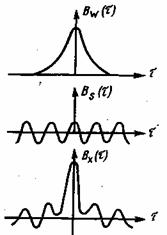
Рис. 4.8. Корреляционная функция сигнала и помехи
Тогда
Функция автокорреляции помехи B
(t) как эргодического процесса убывает три возрастании аргумента т, а функция автокорреляции периодического сигнала есть периодическая функция с тем же периодом (2.23). Функция корреляции принятого сигнала представляет собой сумму этих двух функций (рис. 4.8). Таким образом, при достаточно большом 
можно получить периодическую кривую, соответствующую переданному сигналу s(t), т. е. выделить сигнал из шума. Величина , при которой уже можно пренебречь B(t), зависит от интервала корреляции помехи и отношения сигнала к помехе. Очевидно, чем больше уровень помех, тем больше требуемое время задержки.
4.6. Прием на согласованный фильтр
Существует большой класс задач, в которых требуется обнаружить сигнал, если форма его известна. К их числу относится задача приема телеграфных сигналов, сигналов при импульсно-кодовой модуляции, радиолокационных сигналов. В этих случаях важным параметром, характеризующим качество обнаружения, является отношение сигнала к помехе. Линейный фильтр, максимизирующий это отношение, называется оптимальным согласованным фильтром.
Пусть на входе фильтра действует сумма сигнала s(t) и помехи (t), т. е. колебание x(t)=s(t)+(t). Полезный сигнал s(t) рассматривается не как случайный процесс, а как функция известной формы со спектральной плотностью
где S() и 
— амплитудный и фазовый спектры сигнала. Помеху будем считать стационарным случайным процессом типа белого шума со спектральной плотностью 
Коэффициент передачи линейного фильтра запишем в виде
Сигнал на выходе фильтра, очевидно, равен сумме полезного сигнала yc(t) и помехи yП(t):
Полезный сигнал на выходе можно записать в виде
Пиковая мощность сигнала в некоторый момент 
будет равна:
,
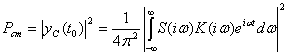а мощность помехи
Тогда превышение сигнала над помехой в момент времени t0 будет определяться следующим выражением:
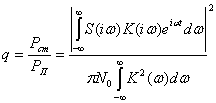(4.32)
Необходимо найти, каким должен быть коэффициент передачи фильтра, чтобы отношение сигнала к помехе q на его выходе было максимальным. На основании неравенства БуняковскогоШварца получаем
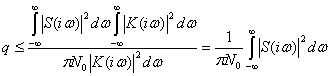(4.33)
Таким образом, при любой характеристике фильтра 
отношение сигнала к помехе не может превосходить максимального значения
(4.34)
где Е — полная энергия сигнала. Указанная максимальная величина q достигается в том случае, когда коэффициент передачи фильтра имеет следующее выражение:
(4.35)
где S(—i)=S()e
—функция, комплексно-сопряженная со спектром сигнала S(i),с— произвольная постоянная. В этом нетрудно убедиться путем непосредственной подстановки выражения (4.35) в равенство (4.32).
Выражение (4.35) можно записать в виде двух равенств:
(4.36)
из которых следует, что амплитудно-частотная характеристика согласованного фильтра с точностью до постоянного множителя совпадает с амплитудным спектром сигнала, а фазо-частотная характеристика определяется фазовым спектром сигнала и линейной функцией частоты 
. Таким образом, частотная характеристика оптимального фильтра полностью определяется спектром сигнала, «согласована» с ним. Отсюда и название — согласованный фильтр.
Фаза сигнала на выходе согласованного фильтра равна:
При t=t, 
=0, т. е. в момент t, все гармонические составляющие сигнала имеют одинаковую фазу и складываются арифметически, образуя в этот момент пик сигнала на выходе фильтра. Спектральные же составляющие помехи на выходе фильтра имеют случайную фазу. Этим и объясняется доказанное выше положение о том, что согласованный фильтр максимизирует отношение сигнала к помехе на выходе.
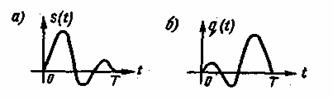
Рис. 4.9. Сигнал s(t) (а) и импульсный отклик согласованного фильтра g(t)(б)
Импульсный отклик согласованного фильтра легко определяется на основании преобразования Фурье. Согласно (4.35) имеем
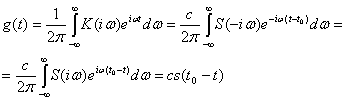(4.37)
Итак, импульсным откликом согласованного фильтра является зеркальное отображение сигнала относительно в масштабе «с»(рис. 4.7). Из рис. 4.9 видно, что t0 не может быть меньше момента окончания сигнала Т. Это означает, что для практически реализуемого фильтра должно выполняться условие 
. Для уменьшения времени анализа целесообразно принять t=T.
Напряжение на выходе согласованного фильтра в некоторый момент времени t согласно интегралу Дюамеля равно:
(4.38)
где 
Равенство (4.38) показывает, что напряжение на выходе согласованного фильтра пропорционально функции взаимной корреляции принятого сигнала x(t) и переданного сигнала s(t). В этом отношении согласованный фильтр адекватен коррелятору.
Сигнал на выходе фильтра (без помех) соответственно будет равен:
(4.39)
Итак, сигнал на выходе согласованного фильтра с точностью до постоянного множителя с совпадает с автокорреляционной функцией входного сигнала. При 
значение функции Bs(0) равно энергии сигнала Е. Следовательно, максимальное значение сигнала на выходе 
. Длительность сигнала на выходе фильтра определяется интервалом корреляции. Дт (2.24). В зависимости от типа сигналов
, где Т — длительность сигнала на входе. Появляется возможность сжатия сигнала
во времени. Так, для шумоподобных сигналов 
. Коэффициент сжатия при этом равен базе сигнала: 
Синтез согласованных фильтров можно производить по импульсному отклику g(t) или спектральным способом по коэффициенту передачи .
В качестве примера рассмотрим построение согласованного фильтра для прямоугольного видеоимпульса, заданного в виде:
при 
s(t) = 0 при 
и t>T
Спектр такого импульса, как известно, 
. На
основании (4.35) коэффициент передачи согласованного фильтра будет
(4.40)
Импульсная переходная характеристика такого фильтра g(t) совпадает по форме с самим сигналом s(t); действительно, из соотношения (4.37) следует, что
g(t)=cs(T-t)=cA при g(t)=0 при t<0 и t>T
Известно, что умножение на 
в частотной области соответствует интегрированию в пределах от 
до 
временной области, а умножение на 
соответствует задержке сигнала на время T.
Следовательно, фильтр с коэффициентом передачи (4.40) состоит из интегратора И, коэффициент передачи которого равен: линии задержки на время Т с коэффициентом передачи
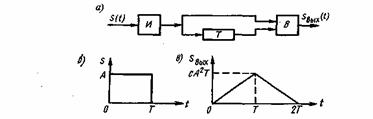
Рис. 4.10. Согласованный фильтр для прямоугольного видеоимпульса (а),сигнал на его входе (б) и выходе (в)
вычитающего устройства В (рис. 4.10а). Сигнал на выходе фильтра согласно (4.39) имеет форму равнобедренного треугольника (рис. 4.106) с основанием 2Т и высотой, равной энергии сигнала сА2Т, т. е.
при = 
при T<t<2T
Рассмотрим второй пример — согласованный фильтр для радиоимпульса. Пусть сигнал задан в виде:
при s(t) = 0 при и t>T
Предположим для простоты, что Т=(2п+1)
, т. е. на интервале (0, Т) укладывается нечетное число полупериодов. Тогда на этом интервале
Такой импульсной реакцией (с точностью до постоянного множителя) обладает колебательный контур без потерь.
Радиоимпульс и соответствующая ему импульсная характеристика фильтра g(t) могут быть представлены как разность двух синусоид, сдвинутых одна относительно другой на время Т.
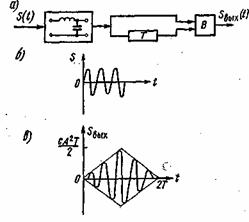
Рис. 4.11. Согласованный фильтр для радиоимпульса (а), сигнал на его входе (б) и выходе (в)
Поэтому схема согласованного фильтра для радиоимпульса (рис. 4.11 а) отличается от схемы рис. 4.10a только тем, что вместо интегратора И включен высокодобротный колебательный контур с собственной частотой 
. Постоянная времени контура, очевидно, должна быть много больше длительности сигнала Т. Если в отрезке времени Т вмещается четное (но целое) число полуволн, то вычитающее устройство должно быть заменено сумматором. При подаче на вход радиоимпульса (рис. 4.116) выходной сигнал 
будет иметь вид, показанный на рис. 4.11б. Этот сигнал совпадает по форме с автокорреляционной функцией входного сигнала Bs(). Максимальное значение сигнала на выходе фильтра
Если длительность импульса не кратна периоду заполнения 
или начальная фаза заполнения такова, что сигнал начинается не с нулевого значения, то схема рис. 4.1 a должна быть дополнена фазокорректирующими элементами.
Рассмотрим теперь сигнал, представляющий собой последовательность п равноотстоящих одинаковых импульсов:
Спектр такого сигнала
где 
— спектр первого импульса, начинающегося в момент 
— спектр второго импульса, начинающегося в момент :t=T
, и т. д. Так как длительность сигнала равна 
, то в соответствии с выражением (4.35) коэффициент передачи согласованного фильтра будет
где 
— коэффициент передачи фильтра, согласованного с первым одиночным импульсом. Выражение в квадратных скобках является геометрической прогрессией. При достаточно большом п
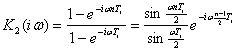
есть не что иное, как коэффициент передачи гребенчатого фильтра. Функция 
имеет максимумы на частотах, кратных периоду повторения импульса 
Таким образом,
Отсюда следует, что согласованный фильтр для последовательности равноотстоящих и одинаковых импульсов может быть осуществлен в виде каскадного соединения согласованного фильтра для одиночного импульса (рис. 4.10а) и гребенчатого фильтра с коэффициентом передачи
Если сигнал представляет собой последовательность радиоимпульсов, то под 
следует понимать коэффициент передачи фильтра, согласованного с первым одиночным радиоимпульсом.
В ряде случаев согласованные фильтры оказываются практически трудно реализуемыми. Поэтому часто применяют фильтры, которые согласованы с сигналом только по полосе (квазиоптимальные фильтры). Оптимальная полоса для различных импульсов различна и может быть вычислена без особых трудностей. Так, для фильтра с прямоугольной частотной характеристикой, на который воздействует радиоимпульс прямоугольной формы длительности
, оптимальная полоса равна 
Можно показать, что отношение сигнала к помехе на выходе квазиоптимального фильтра по сравнению с согласованным фильтром уменьшается на величину порядка 15—20% [8].
4.7. Обобщенный анализ и сравнение различных методов приема
Все изложенные выше методы приема сигнала объединены общей математической операцией интегрирования функций, описывающих сигнал и опорное колебание. В общем виде эта операция сводится к нахождению скалярного произведения
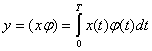(4.41)
где x(t)=s(t) + (t) — аддитивная смесь сигнала и помехи (принятый сигнал), 
(t) — весовая функция (опорное колебание).
Если (t) = 1, то имеет место интегральный прием, если (t) =s(t) — когерентный прием, при (t) =s(t—) — корреляционный, а при (t)=c(t—) — автокорреляционный приемы. В случае, когда (t) совпадает с импульсной характеристикой g(t)=s(t—t), оператор (4.41) описывает прием на согласованный фильтр.
Поскольку операция (4.41) является линейной, то величина у распадается на два слагаемых, из которых одно (b) зависит только от сигнала, а другое (|) — только от помехи:
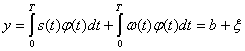(4.42)
В этих условиях можно говорить об отношении сигнала к помехе на выходе приемника (точнее, на входе решающего устройства) и определить его по формуле
(4.43)
При этом мы считаем, что сигнал и помеха независимы, 
и 
. Теперь можно решить задачу отыскания оптимального метода приема (оптимальной обработки), при котором обеспечивается наибольшее отношение сигнал/помеха на выходе приемника.
Выберем весовую функцию (t) так, чтобы максимизировать полезный сигнал b, т. е. функционал
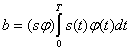(4.44)
Это, вообще говоря, вариационная задача, но она решается очень просто, если перейти к геометрическим представлениям. Так как 'скалярное произведение (s) пропорционально проекции одного вектора на другой, то величина b будет иметь наибольшее значение, когда оба вектора s и совпадают по направлению, т. е.
(4.45)
Равенство (4.45) показывает, что (t)=ks(t), где k — коэффициент пропорциональности. Таким образом, максимальное значение полезного сигнала достигается, как и следовало ожидать, при когерентном методе приема, когда 
Теперь определим дисперсию помехи, выражаемой интегралом
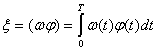(4.46)
Составим квадрат этой величины
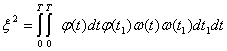
Усредняя, находим
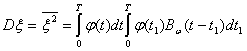(4.47)
где 
—функция автокорреляции помехи.
Если воспользоваться зависимостью (2.82) между функцией корреляции и энергетическим спектром случайного процесса, то можно выразить дисперсию помехи через спектры. Подставив выражение (2.82) в (4.47), получим
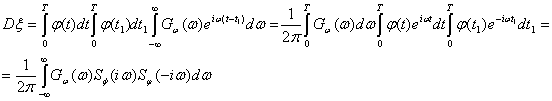
где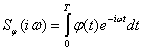 
— текущий спектр функции (t),а 
— комплексно-сопряженный спектр. Итак,
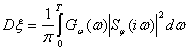(4.48)
Эта формула является также общей, как и ф-ла (4.47), из которой она получена. Выразим сигнал через спектр
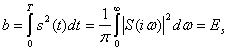(4.49)
(4.49) е
S(ico)
На основании (4.43), (4.48) и (4.49), получаем общее выражение для отношения сигнала к помехе
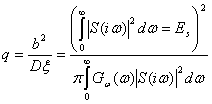(4.50)
При помощи неравенства Буняковского можно получить для выражения (4.50) следующую оценку:
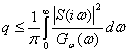(4.51)
В частном случае помехи с равномерным спектром, когда
, имеем
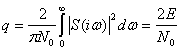
что совпадает с выражением (4.34) для согласованного фильтра.
Установим связь между интегрированием и фильтрацией сигнала. При обработке сигнала интегрированием 
согласно (4.41) получаем
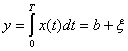
где
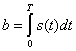
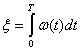
Если S(i)— спектральная плотность сигнала s(t), то на основании преобразования Фурье имеем
Подставив это значение s(t) в выражение для b и выполнив интегрирование по t получим
(4.52)
где
(4.53)
Из соотношения (4.52) следует, что интегрирование в интервале времени от 0 до Т эквивалентно фильтрации сигнала фильтром с коэффициентом передачи K(i)— определяемым выражением (4.53). Сравнение выражений (4.40) и (4.53) показывает, что они различаются только постоянными множителями. Следовательно, фильтру с коэффициентом передачи (4.53) соответствует схема рис. 4.10а.
Шум на выходе интегратора является случайной величиной. Дисперсия такой величины определяется соотношением (4.4). Функция автокорреляции шума на входе интегратора согласно (2.82)
Подставив это выражение в (4.4) и выполнив интегрирование по t и t получим
где
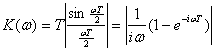
— модуль коэффициента передачи. Следовательно, интегрирование шума также эквивалентно фильтрации его в схеме рис. 4.10а.
В предыдущем параграфе было показано, что данная схема является согласованным фильтром для прямоугольного видеосигнала при наличии белого шума. Это означает, что для указанных условий операция интегрирования является оптимальной.
При синхронном детектировании фильтрация (интегрирование) до детектора практически равноценна по помехоустойчивости фильтрации (интегрированию) после детектора.
При несинхронном (амплитудном) детектировании необходимо считаться с явлением подавления сигнала помехой при малых значениях отношения сигнал/помеха. В этом случае фильтрация и интегрирование до детектора могут обеспечить более высокую помехоустойчивость приемника, чем фильтрация или интегрирование после детектора.
4.8. Оптимальная фильтрация непрерывных сигналов
Задача оптимальной фильтрации непрерывного сигнала ставится следующим образом: требуется так обработать принятый сигнал x(t)=s(t)+ (t), чтобы получить на выходе приемника сигнал y(t), наименее отличающийся от переданного сигнала s(t). Математическое решение этой задачи было дано А. Н. Колмогоровым и Н. Винером. Теория Колмогорова—Винера базируется на трех основных предположениях: 1) сигнал s(t) и помеха (t) представляют собой стационарные случайные процессы; 2) операция фильтрации предполагается линейной; 3) критерием оптимальности считается минимум среднеквадратической ошибки.
Пусть сигнал s(t) и шум (t) являются независимыми случайными процессами с известными корреляционными функциями Bs(t) и Bw(), a x(t) — сигнал на входе линейного фильтра с импульсной характеристикой g(t). Требуется найти такую функцию g(t), чтобы сигнал на выходе фильтра y(t) минимизировал среднеквадратическую ошибку
Требование физической реализуемости фильтра, как известно, сводится к тому, что импульсная реакция фильтра должна удовлетворять условию g(t)=0 для всех t<0. Это ограничение учитывается в записи
где область интегрирования 
для физически реализуемого фильтра есть интервал от 0 до , а для нереализуемого фильтра — от до
Докажем вначале, что характеристика фильтра g(t) оптимальна тогда и только тогда, когда
для из (4.54)
т. е. когда ошибка 
(t)=y(t)—s(t) некоррелирована со входным сигналом x(t) во все моменты времени в области
Пусть 
— импульсная характеристика оптимального фильтра, для которого справедливо условие (4.54), а для 
— импульсная характеристика любого другого линейного фильтра. Отклики фильтров соответственно обозначим через y(t) и y
(t) Тогда
Так как функция 
и (t) удовлетворяет (4.54), то
Следовательно,
Очевидно это выражение будет минимальным, когда 
что и доказывает справедливость условия (4.54).
Представим соотношение (4.54) в виде 
отсюда получаем
или
(4.55)
В случае, когда сигнал s(t) и помеха w(i) независимы, ур-ние (4.55) принимает вид
(4.56)
Это интегральное уравнение является основным уравнением теории линейной фильтрации и называется уравнением Винера — Хопфа. Его решением является искомая функция g(t), минимизирующая среднеквадратическую ошибку 
2.
Уравнение (4.56) решается сравнительно просто, если 
, т. е. для нереализуемых фильтров. Для реализуемых фильтров задача существенно усложняется. Ниже приводится упрощенная теория линейной фильтрации [12, 13].
Квадрат среднеквадратической ошибки может быть выражен через энергетический спектр ошибки:
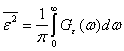(4.57)
где
— энергетический спектр функции (t)=y(t)—s(t—t) ,t0 — время задержки сигнала.
Определим сначала функцию корреляции ошибки
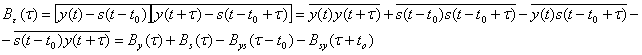
(4.58)
Так как преобразование Фурье, связывающее между собой B() и
G() линейно, то для спектра ошибки имеем
(4.59)
Выражение для Gу() находим непосредственно по ф-ле (2.109):
Так как s(t) и (t) независимы, то 
и 
Остается найти взаимные спектральные плотности Gsy и Gys. Согласно (2.8,1) имеем
(4.60)
Но отклик фильтра y(t) выражается интегралом Дюамеля
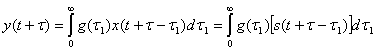(4.61)
После подстановки (4.61) в выражение (4.60), учитывая, что 
и импульсная реакция фильтра g(t) связана с коэффициентом передачи К(i) парой, преобразований Фурье, получим
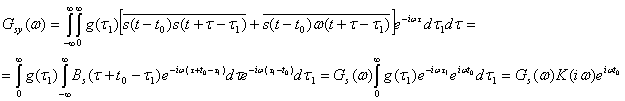
Так как К(i) =
, тo 
Энергетический спектр 
есть действительная величина, поэтому мнимый показатель экспоненты должен быть равен нулю, т. е.
(4.62)
Выражение (4.62) определяет фазовую характеристику оптимального фильтра. Итак,
Аналогично определяется 
Легко показать, что
Окончательно выражение (4.59) для спектра погрешности принимает вид 
Теперь нужно найти такое значение К(), при котором среднеквадратическая погрешность 2 (4.57) будет наименьшей. Для этого достаточно минимизировать G
. Перепишем выражение для в виде
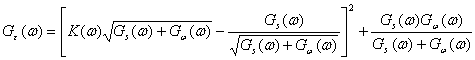
Первый член положителен и зависит от К(), второй член — заданная величина. Ясно, что наименьшее значение будет иметь тогда, когда выражение в квадратных скобках будет равно нулю. При этом условии
или с учетом (4.62)
(4.63).
При этом спектр ошибки
(4.64).
а средний квадрат ошибки равен:
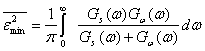(4.65).
Заметим, что сигнал может быть полностью отделен от помехи, т.е. ошибка будет равна нулю лишь при условии 
. Последнее означает, что спектры сигнала и помехи не перекрываются (рис. 4.12а). Если помеха отсутствует, то 
,
, 
=1 т. е. фильтра не требуется.
Фильтр с оптимальной характеристикой (4.63) пропускает колебание различных частот с тем меньшим весом, чем больше отношение 
при данной частоте. Например, если спектры сигнала и помехи перекрываются, как показано на рис. 4.126, то частотная характеристика фильтра должна иметь вид, показанный на том же рисунке пунктиром. Если отношение сигнала к помехе мало:
то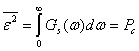 
т. е. погрешность очень велика и восстановление сигнала при помощи фильтрации становится невозможным.
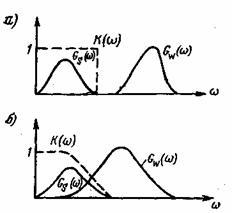
Рис. 4.12. Частотная характеристика оптимального фильтра: спектры сигнала и помехи не перекрываются (а), спектры сигнала и помехи перекрываются (б).
Можно получить лучший результат при фильтрации, если применить так называемое предыскажение. Передача с предыскажением состоит в том, что и на передающей стороне сигнал s(t) пропускается через фильтр с коэффициентом передачи
. Полученный таким образом видоизмененный сигнал передается по каналу. На приемной стороне ставится другой фильтр С коэффициентом передачи К- Характеристики фильтров Ки К выбираются так, чтобы обеспечить минимум среднеквадратической ошибки. Расчеты показывают [12], что предыскажение дает тем больший выигрыш, чем меньше относительная ширина полосы перекрытия спектров сигнала и помехи
Вопросы для повторения
1. Какие виды обработки дискретных сигналов Вам известны?
2. Что называется оптимальной обработкой сигналов?
3. При каких условиях суммирование отсчетных значений сигнала эквивалентно интегрированию?
4. В чем отличие когерентного приема от некогерентного?
5. В чем выражается явление подавления сигнала помехой? При каком детектировании это имеет место?
6. Изобразите структурные схемы корреляционного и автокорреляционного приемников.
7. Чем можно объяснить ухудшение помехоустойчивости при переходе от корреляционного приема к автокорреляционному?
8. Как определяются импульсная реакция и коэффициент передачи согласованного фильтра?
9. Чему равно максимальное напряжение на входе согласованного фильтра?
10. Укажите одну из возможных реализаций согласованного фильтра для периодической последовательности одинаковых импульсов.
11. Что мы называем квазиоптимальным фильтром? В чем состоят недостатки и преимущества таких фильтров?
12. Запишите линейный функционал, описывающий работу различных способов приема. Какой вид имеет весовая функция при интегральном приеме, когерентном и автокорреляционном приемах?
13. Что мы называем линейным оптимальным фильтром Колмогорова-Винера? Чем определяются коэффициент передачи и минимальная среднеквадратичная ошибка такого фильтра?
14. Почему фильтрация (интегрирование) до детектора более предпочтительна, чем фильтрация (интегрирование) после детектора?