Рассмотрим линейную систему, импульсная реакция которой g(t) или коэффициент передачи К(iω) известны. Напомним, что К(iω) и g(t) связаны между собой преобразованием Фурье:

= £•

На вход системы поступает стационарный случайный сигнал x(t) с заданными характеристиками. На выходе системы получаем некоторый случайный сигнал y(t). Согласно теореме Дюамеля

y(t)=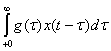 Найдем функцию автокорреляций сигнала

на выходе линейной системы

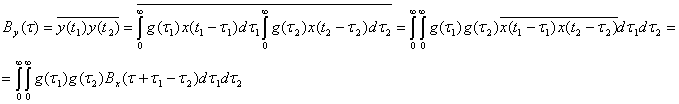(2.107)

где

Таким образом, By(τ) зависит не от и в отдельности, а от их разности т. Следовательно, при воздействии случайного стационарного процесса на линейную систему на выходе получается также стационарный случайный процесс y(t) с функцией корреляции, определяемой выражением (2.107).

Мощность выходного сигнала согласно (2.107) равна:

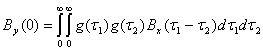(2.108)

Эта формула показывает, что для определения мощности выходного сигнала недостаточно знать В(0) входного сигнала — нужно знать всю функцию автокорреляции В(τ).

Связь между энергетическими спектрами сигнала на входе и выходе линейной системы может быть записана в виде

(2.109)

Действительно, согласно (2.82) и (2.107) имеем

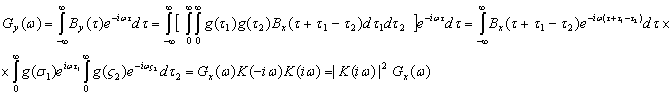
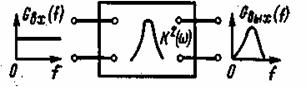
Рис. 2.9. Энергетический спектр шума на входе и выходе линейной системы

Из полученной формулы следует, что фазовая характеристика системы не оказывает влияния на энергетический спектр выходного сигнала. Пусть на вход линейной системы с коэффициентом передачи К(iω) воздействует белый шум с равномерным спектром gx(u) =(1/2)N0. Энергетический спектр выходного процесса согласно (2.109) будет gy(u) =(1/2)N0.Спектр помехи на выходе системы в этом случае повторяет по своей форме частотную характеристику системы с возведенными в квадрат ординатами (рис. 2.9). Мощность шума на выходе при этом равна:

(2.110)

Или, вводя эффективную полосу пропускания системы

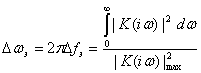(2.111)

получаем

(2.112)

Закон распределения вероятностей случайного процесса (сигнала или помехи) на выходе линейной системы в общем случае отличается от закона распределения вероятностей процесса на входе. В одном очень важном случае закон распределения при линейных преобразованиях не изменяется. Это — случай гауссова процесса. Если процесс на входе линейной системы имеет нормальное распределение, то он остается нормальным и на выходе. Изменяются только параметры процесса — дисперсия (мощность) и функция корреляции в соответствии с выражениями (2.107) и (2.108).

В случае узкополосной системы, когда полоса пропускания системы много меньше ширины спектра процесса на входе, имеет место явление нормализации закона распределения. Это явление состоит в том, что закон распределения процесса на выходе узкополосной системы сходится к нормальному независимо от того, Какое распределение имел процесс на входе. Физически это можно пояснить так. Отдельные возмущения на выходе системы, вызванные хаотическими воздействиями входного процесса, не успевая затухать, накладываются друг на друга и образуют новый процесс. Согласно предельной теореме вероятностей закон распределения этого процесса, представляющего собой сумму большого числа независимых случайных величин (возмущений), стремится к нормальному.

Рассмотрим теперь, как воздействует случайный процесс на нелинейную систему. В общем случае эта задача очень трудная. Дело обстоит значительно легче, когда речь идет о безинерционных нелинейных системах, в которых выходной процесс y(t) в данный момент однозначно определяется входным процессом x(t) в тот же момент времени. Пусть известны характеристика нелинейного устройства y=f(x) и статистические свойства входного процесса x(t). Необходимо определить статистические свойства выходного процесса y(t). В принципе, эта задача сводится к преобразованию переменных.

Рассмотрим простейший пример одномерной случайной величины. Известна плотность вероятности р(х) случайной величины х и нужно найти плотность вероятности р(у) случайной величины, у=S(х). Предположим, что существует однозначная обратная функция x=φ(y). Так как случайные величины связаны однозначной функциональной зависимостью, то из факта того, что х заключено в достаточно малом интервале (х0, х0+dx), следует, что величина и будет находиться в интервале (у0, у0+dy), где у0=f(x0). Следовательно, вероятности этих двух событий p(y)dy=p(x)dx, т. е.

(2.113)

Поскольку плотности вероятности не могут быть отрицательными, то в ф-лу (2.113) следует подставить модуль производной. Далее можно определить среднее значение выходного процесса (постоянную составляющую)

(2.114)

Аналогично определяются полная мощность процесса

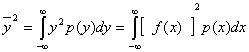(2. 115)

и функция корреляции

(2.116)

Энергетический спектр выходного процесса определяется с помощью преобразования Фурье от функции корреляции.

Спектр процесса на выходе нелинейной системы существенно отличается от спектра на входе вследствие появления новых частотных составляющих, которые отсутствовали во входном процессе. Спектр обычно содержит низкочастотные составляющие вблизи нулевой частоты и участки высокочастотных составляющих.

Таким образом, при воздействии случайного процесса на нелинейную систему изменяются спектр процесса, законы распределения вероятностей и все связанные с ними параметры процесса.