15.1. Сложности связи по каналу с замираниями

15.2. Описание распространения радиоволн в мобильной связи

15.3. Расширение сигнала во времени

15.3.1. Расширение сигнала во времени, рассматриваемое в области задержки

15.3.1.1. Категории ухудшения качества передачи вследствие расширения сигнала во времени, рассматриваемого в области задержки

15.3.2. Расширение сигнала во времени, рассматриваемое в частотной области

15.3.2.1. Категории ухудшения качества передачи вследствие расширения сигнала во времени, рассматриваемого в частотной области

15.3.3. Примеры амплитудного и частотно-селективного замирания

15.4. Нестационарное поведение канала вследствие движения

15.4.1. Нестационарное поведение канала, рассматриваемое во временной области

15.4.1.1. Независимость основных проявлений замирания

15.4.1.2. Понятие дуальности

15.4.1.3. Категории ухудшения качества передачи вследствие нестационарного поведения канала, рассматриваемого во временной области

15.4.2. Нестационарное поведение канала, рассматриваемое в области доплеровского сдвига

15.4.2.1. Аналогия спектрального расширения в каналах с замираниями

15.4.2.2. Категории ухудшения характеристик вследствие нестационарной природы канала, рассматриваемые в области доплеровского сдвига

15.4.3. Релеевский канал с медленным и амплитудным замиранием

15.5. Борьба с ухудшением характеристик, вызванным эффектами замирания

15.5.1. Борьба с частотно-селективными искажениями

15.5.2. Борьба с искажениями, вызванными быстрым замиранием

15.5.3. Борьба с уменьшением SNR

15.5.4. Методы разнесения

15.5.4.1. Комбинированные методы разнесения

15.5.5. Типы модуляции для каналов с замираниями

15.5.6. Роль чередования

15.6. Краткий обзор ключевых параметров, характеризующих каналы с замираниями

15.6.1. Искажения вследствие быстрого замирания: случай 1

15.6.2. Искажения вследствие частотно-селективного замирания: случай 2

15.6.3. Искажения вследствие быстрого и частотно-селективного замирания: случай 3

15.7. Приложения: борьба с эффектами частотно-селективного замирания

15.7.1. Применение эквалайзера Витерби в системе GSM

15.7.2. RAKE-приемник в системах с расширением спектра методом прямой последовательности

15.1. Сложности связи по каналу с замираниями

При анализе характеристик систем связи отправной точкой является описание основных характеристик в классическом (идеальном) канале с белым аддитивным гауссовым шумом (additive white Gaussian noise — AWGN) со статистически независимыми гауссовыми шумовыми выборками, искажающими информационные выборки, и отсутствием межсимвольной интерференции (intersymbol interference — ISI). Основным источником ухудшения характеристик является тепловой шум, генерируемый в приемнике. Другим источником потерь являются естественные и искусственные источники шума и помех, воздействие которых на принимающую антенну можно качественно описать через параметр, называемый температурой антенны. Тепловой шум имеет, как правило, плоскую спектральную плотность мощности по всей полосе сигнала и гауссову функцию плотности вероятности напряжения с нулевым средним. В системах мобильной связи внешние шумы и помехи часто оказываются более значительными, чем тепловой шум приемника. При моделировании реальных систем следующим шагом является введение полосовых фильтров. Обычно фильтрация в передатчике служит для удовлетворения некоторых условий к спектральным составляющим. Фильтрация в приемнике часто является результатом применения согласованного фильтра. Из-за ограниченности полосы частот и фазовых искажений в фильтрах для снижения ISI, вызываемой фильтром, может потребоваться специальная обработка сигнала и его выравнивание.

Если характеристики радиоканала не заданы, то обычно подразумевается, что сигнал затухает с расстоянием так же, как при распространении в идеальном свободном пространстве. В модели свободного пространства область между антеннами передатчика и приемника предполагается свободной от объектов, которые могли бы поглощать или отражать энергию на радиочастотах. Предполагается также, что внутри этой области атмосфера ведет себя как совершенно однородная непоглощающая среда. Кроме того, считается, что земля находится бесконечно далеко от распространяемого сигнала (или, что равносильно, имеет пренебрежимо малый коэффициент отражения). По существу, в этой идеализированной модели свободного пространства ослабление между передатчиком и приемником радиочастотной энергии происходит по закону обратных квадратов. Мощность приемника, выраженная через переданную мощность, ослабляется в Ls(d)) раз, причем данный параметр называется потерями в тракте (path loss), или потерями в свободном пространстве (free space loss). Если антенна приемника изотропна, то этот коэффициент выражается следующим образом.

(15.11)

Здесь d — это расстояние между передатчиком и приемником, а — длина волны распространяемого сигнала. При таком идеальном распространении мощность полученного сигнала весьма предсказуема. Для большинства реальных каналов, в которых распространение происходит в атмосфере и вблизи поверхности земли, модель распространения в свободном пространстве неадекватно описывает поведение канала и не позволяет предсказывать характеристики системы. В системах мобильной радиосвязи сигнал может передаваться от передатчика к приемнику по множеству отражательных путей. Это явление, называемое многолучевым распространением (multipath propagation), может вызывать флуктуации амплитуды, фазы и угла прибытия полученного сигнала, что определило название замирание вследствие многолучевого распространения (multipath fading). Другое название — сцинтилляция (scintillation) — которое происходит из радиоастрономии, используется для описания замирания, вызванного физическими изменениями в среде распространения, такими как изменение электронной плотности слоев ионосферы, которые отражают высокие частоты радиосигналов. Как замирание, так и сцинтилляция относится к случайным флуктуациям сигнала; основное отличие заключается в том, что явление сцинтилляции объясняется механизмами, существенными на расстояниях, намного меньших длины волны (например, движение электронов). Прямое моделирование и проектирование систем, включающих методы борьбы с замиранием, обычно сложнее разработки систем, где единственным источником ухудшения рабочих характеристик считается шум AWGN.

15.2. Описание распространения радиоволн в мобильной связи

На рис. 15.1 представлен обзор проявления эффектов замирания в каналах. Он начинается с двух типов эффектов замирания, характерных для мобильной связи: крупномасштабное и мелкомасштабное замирание. Крупномасштабное замирание отражает среднее ослабление мощности сигнала или потери в тракте вследствие распространения на большое расстояние. На рис. 15.1 проявления крупномасштабного замирания показаны в блоках 1-3. На это явление влияют выступающие наземные элементы (например холмы, леса, рекламные щиты, группы строений и т.д.) между передатчиком и приемником. Часто говорят, что приемник "затеняется" этими выступами. Статистика крупномасштабного замирания позволяет приблизительно рассчитать потери в тракте как функцию расстояния. Это часто описывается через средние потери в тракте (степенной закон п-го порядка) и логарифмически нормально распределенные отклонения от среднего. Мелкомасштабное замирание — это значительные изменения амплитуды и фазы сигнала, которые на практике могут быть результатом небольших изменений (порядка половины длины волны) расстояния между передатчиком и приемником. Как указано на рис. 15.1 (блоки 4-6), мелкомасштабное замирание проявляется двумя способами — расширение сигнала во времени (или дисперсия сигнала) и нестационарное поведение канала. В мобильной радиосвязи параметры каналов изменяются во времени, поскольку движение передатчика и/или приемника приводит в результате к изменению пути распространения. Скорость изменения таких условий распространения определяет скорость замирания (скорость изменения ухудшения характеристик вследствие замирания). Мелкомасштабное замирание называется релеевским, если имеется большое число многократно отражающихся путей и нет компонента сигнала вдоль луча обзора; огибающая такого полученного сигнала статистически описывается с помощью релеевской функции плотности вероятности. Если преобладает незамирающий компонент сигнала, такой как путь распространения вдоль луча обзора, огибающая мелкомасштабного замирания описывается функцией плотности вероятности Раиса [1]. Иными словами, статистики мелкомасштабного замирания всегда распределены по Релею, если путь распространения вдоль луча обзора блокирован, в противном случае имеем распределение Раиса. Мобильный радиоприемник, который перемещается по большому пространству, должен иметь возможность обрабатывать сигналы, подвергнувшиеся замиранию обоих типов (мелкомасштабное, наложенное на крупномасштабное).

Крупномасштабное замирание (ослабление или потери в тракте) можно рассматривать как пространственное усреднение мелкомасштабных флуктуаций сигнала. Оно вычисляется, как правило, путем усреднения полученного сигнала по интервалу, превышающему 10-30 длин волн, чтобы отделить мелкомасштабные (главным образом релеевские) флуктуации от крупномасштабных эффектов затенения (обычно с логарифмически нормальным распределением). Существует три основных механизма, воздействующих на распространение сигнала в системах мобильной связи [1].

• Отражение (reflection) происходит тогда, когда распространяющаяся электромагнитная волна сталкивается с гладкой поверхностью, размер которой гораздо больше длины волны радиочастотного сигнала ().

• Дифракция (diffraction) встречается тогда, когда путь распространения между передатчиком и приемником преграждается плотным телом, размеры которого велики по сравнению с , что вызывает появление вторичных волн, образующихся позади преграждающего тела. Дифракция — это явление, которое является причиной того, что распространение радиочастотной энергии от передатчика к приемнику происходит в обход пути прямой видимости между ними. Ее часто называют затенением (shadowing), поскольку дифрагированное поле может достичь приемника, даже если оно затенено непроницаемой преградой.

• Рассеяние (scattering) встречается тогда, когда радиоволна сталкивается с любой неровной поверхностью или с поверхностью, размеры которой равны порядка или меньше, что приводит к распространению (рассеянию) или отражению энергии во всех направлениях. В городской местности обычные препятствия, вызывающие рассеивание сигнала, — это фонарные столбы, уличные знаки и листья. Название рассеивающий элемент (scatterer) применимо к любым препятствиям на пути распространения, которые являются причиной отражения или рассеяния сигнала.

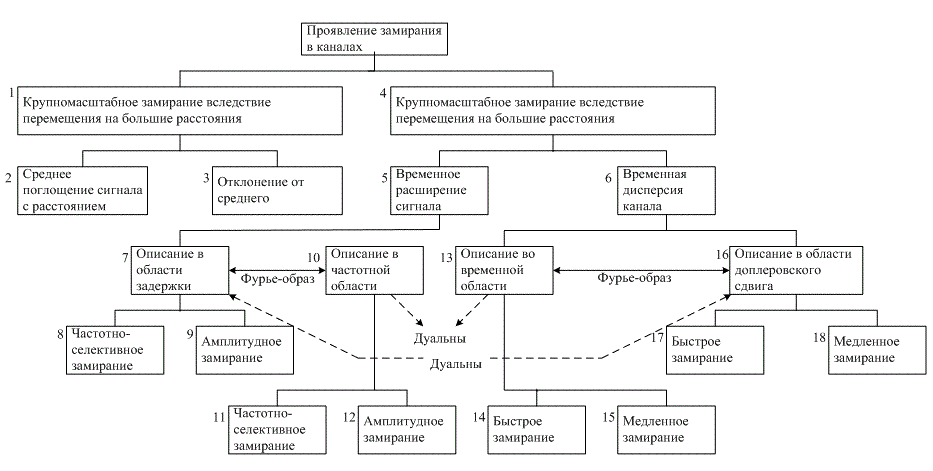
Рис. 15.1 Проявление замирания в канале

Рис. 15.1 можно использовать как оглавление следующих разделов. Два проявления мелкомасштабного замирания, временное расширение сигнала (дисперсия сигнала) и нестационарное поведение канала, будут исследованы в двух областях:, временной и частотной, как указано в блоках 7, 10, 13 и 16 (рис. 15.1). При дисперсии сигнала типы ухудшений характеристик, возникающих вследствие замирания, разделены на частотно-селективные или частотно-неселективные (амплитудные), как показано в блоках 8, 9, 11 и 12. При переменном во времени поведении типы ухудшений характеристик, возникающих вследствие замирания, разделены на быстрые и медленные, как показано в блоках 14, 15, 17 и 18. Пометки "Фурье-образы" и "дуальны" будут объяснены позже.

Удобной (но не совсем точной) иллюстрацией является рис. 15.2, показывающий различные вклады, которые должны рассматриваться при оценке потерь в тракте при анализе бюджета линии связи для мобильной радиосвязи [2]: (1) средние потери в тракте в результате крупномасштабного замирания как функция расстояния, (2) резерв крупномасштабного замирания в расчете на (почти) наихудший вариант отклонения от средних потерь в тракте (обычно 6-10 дБ) и (3) резерв релеевского или мелкомасштабного замирания в расчете на (почти) наихудший вариант (обычно 20-30 дБ). На рис. 15.2 примечание "= 1-2%" указывает предложенную область (вероятность) под хвостом каждой функции распределения вероятности, используемую как задачу разработки. Таким образом, величина указанного резерва предназначена для обеспечения достаточной мощности полученного сигнала для приблизительно 98-99% возможных значений замирания (крупно- и мелкомасштабного).

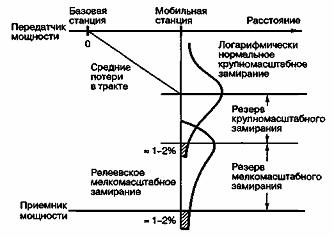
Рис. 15.2. Замирание в канале через бюджет линии связи.

(Источник: Greenwood D. and Hanto L. "Characterization: of Mobile Radio Channels". Mobile Radio Communications, edited by R. Steele,

Chapter 2, Pentech Press, London, 1994.)

С помощью комплексной формы записи переданный сигнал можно представить следующим образом.

s(t) = Re (15.2)

g(t) = (15.3)

где R(t) = |g(t)| — модуль огибающей, а — ее фаза. Для чистого фазово- или частотно-модулированного сигнала R(t) будет постоянным и в общем случае будет медленно изменяться по сравнению с t = 1/fc.

В среде с замиранием g(t) изменится на комплексный безразмерный множитель (его происхождение будет показано позже). Модифицированный узкополосный сигнал можно записать в виде . Рассмотрим амплитуду (t)R(t) этой огибающей, которую можно выразить через три положительных члена [3].

(t)R(t) = m(t)r0(t) R(t) (15.4)

Здесь m(t) называют компонентом крупномасштабного замирания огибающей, а r0(t) - компонентом мелкомасштабного замирания. Иногда m(t) именуют локальным средним, или логарифмически нормальным замиранием, поскольку его измеряемые значения можно статистически описать с помощью логарифмически нормальной функции распределения вероятностей; или, что равносильно, при измерении в децибелах m(t) имеет гауссову функцию распределения вероятностей. Кроме того, r0(t) иногда называют замиранием вследствие многолучевого распространения, или релеевским замиранием. На рис. 15.3 показана связь между (t) и m(t) для мобильной радиосвязи. В этом рисунке учтено, что была передана немодулированная несущая волна, а это в контексте уравнения (15.4) означает, что в любое время R(t) = 1. Типичный график зависимости мощности полученного сигнала от смещения антенны (обычно в единицах длины волны) показан на рис. 15.3, а. Мощность полученного сигнала является, конечно, функцией множителя (t). Можно без труда определить мелкомасштабные замирания, наложенные на крупномасштабные. Обычное изменение положения антенны, соответствующее переходу между соседними нулями изменения интенсивности сигнала вследствие мелкомасштабного замирания, равно приблизительно половине длины волны. На рис. 15.3, б крупномасштабное замирание или локальное среднее m(t) было удалено, чтобы показать мелкомасштабное замирание r0(t), относящееся к некоторой постоянной средней мощности. Напомним, что m(t) можно, как правило, оценить с помощью усреднения принятой огибающей по 10-30 длинам волн. Логарифмически нормально распределенное замирание является относительно медленно изменяющейся функцией местоположения. Следует отметить, что в приложениях, включающих движение, таких как использование радио в движущейся машине, зависимость от местоположения равносильна зависимости от времени. Ниже приведены некоторые подробности, касающиеся статистики и механизмов крупномасштабного и мелкомасштабного замираний.

15.3. Расширение сигнала во времени

15.3.1. Расширение сигнала во времени, рассматриваемое в области задержки

Простой способ моделирования явлений замирания был предложен Белло (Bello) [13] в 1963 году; он ввел понятие стационарного в широком смысле некоррелированного рассеяния (wide-sense stationary uncorrelated scattering — WSSUS). В такой модели сигналы, поступающие на антенну приемника с различными задержками, рассматриваются как некоррелирующие. Можно показать [2, 13], что такие каналы являются эффективно стационарными в широком смысле, как во временной, так и в частотной области. Применив такую модель к каналу с замиранием, Белло смог определить функции, которые применимы для любого момента времени и любой частоты. На рис. 15.8 для мобильного канала указаны четыре такие функции, составляющие названную модель [2, 10, 13-15]. Рассмотрим функции, начиная с рис. 15.8, а и двигаясь против часовой стрелки в направлении рис. 15.8, г.

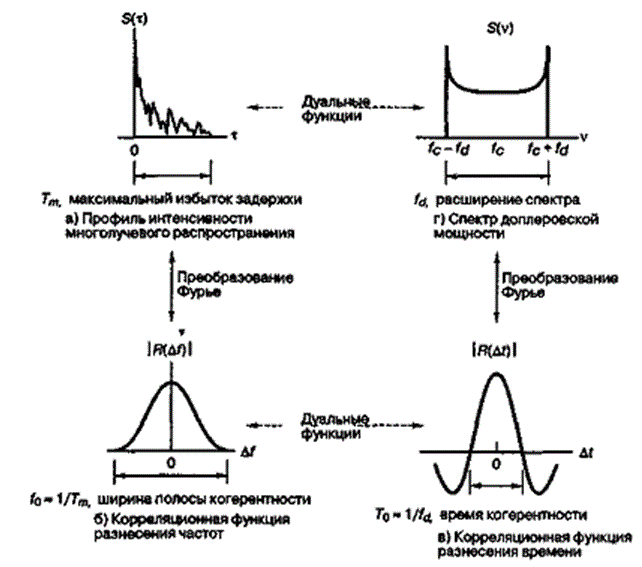
Рис. 15.8. Соотношения между корреляционными функциями канала и функциями плотности мощности

На рис. 15.8, а отображен профиль интенсивности многолучевого распространения (зависимость S() от задержки ). Зная S(), можно определить, как для переданного импульса полученная мощность зависит от временной задержки . Термин "временная задержка" (time delay) используется для обозначения избыточной задержки распространения сигнала. Он представляет задержку данного сигнала относительно времени поступления на приемник первого сигнала. Для типичного беспроводного канала полученный сигнал обычно состоит из нескольких дискретных многолучевых компонентов, приводящих к появлению изолированных пиков S(), называемых иногда пальцами, или отраженными сигналами. Для некоторых каналов, таких как тропосферный канал с рассеянием, принятые сигналы выглядят как континуум многолучевых компонентов [10, 15]. В таких случаях S() — это относительно гладкая (непрерывная) функция . Для измерения профиля интенсивности многолучевого распространения необходимо воспользоваться широкополосными сигналами (импульсы или сигналы с расширенным спектром) [15]. Для единичного переданного импульса время Тm между приемом первого и последнего компонентов представляет собой максимальную избыточную задержку распространения, после которой мощность многолучевого сигнала падает ниже определенного порогового уровня относительно самого мощного компонента. Пороговый уровень можно выбрать на 10 или 20 дБ ниже уровня самого мощного луча. Отметим, что в идеальной системе (нулевая избыточная задержка) функция S() состояла бы из идеального импульса с весовым коэффициентом, равным общей средней мощности полученного сигнала.

15.3.1.1. Категории ухудшения качества передачи вследствие расширения сигнала во времени, рассматриваемого в области задержки

В канале с замираниями взаимосвязь между максимальной избыточной задержкой распространения Тm и временем передачи символа Тs можно рассматривать с позиции двух различных категорий ухудшения качества передачи: частотно-селективного замирания (frequency-selective fading) и частотно-неселективного (frequency nonselective fading), или амплитудного замирания (flat fading) (см. рис. 15.1, блоки 8 и 9, и рис. 15.7). Говорят, что канал обнаруживает частотно-селективное замирание, если Тт > Ts. Это условие реализуется, когда полученный многолучевой компонент символа выходит за пределы длительности передачи символа. Такая многолучевая дисперсия порождает тот же тип искажений ISI, что и электронный фильтр. Фактически другим названием этой категории ухудшения передачи вследствие замирания является вводимая каналом ISI. При частотно-селективном замирании возможно уменьшение искажений, поскольку многие многолучевые компоненты разрешаются приемником. (Несколько подобных методов борьбы с замиранием описаны в следующих разделах.)

Говорят, что канал является частотно-неселективным или проявляется амплитудное замирание, если Тт < Ts. В этом случае все полученные многолучевые компоненты символа поступают в течение времени передачи символа; поэтому компоненты не разрешаются. В данном случае отсутствуют искажения за счет вводимой каналом ISI, так как расширение сигнала во времени не приводит к существенному наложению соседних полученных символов. Однако ухудшение характеристик все же имеет место, поскольку неразрешенные компоненты вектора сигнала могут деструктивно суммироваться, что приводит к значительному уменьшению SNR. К тому же сигнал, классифицированный как проявляющий амплитудное замирание, может иногда испытывать частотно-селективное замирание. Это будет объяснено позже, при рассмотрении ухудшения характеристик в частотной области, в которой такие явления описываются проще. При уменьшении SNR за счет амплитудного замирания можно использовать специальные методы подавления замирания, улучшающие принимаемое значение SNR (или уменьшающие требуемое SNR). Для цифровых систем наиболее эффективным способом является введение каких-либо форм разнесения сигналов и использование кодов коррекции ошибок.

15.3.2. Расширение сигнала во времени, рассматриваемое в частотной области

Полностью аналогичное описание дисперсии сигнала можно привести и в частотной области. На рис. 15.8, б можно видеть функцию ||, обозначенную как корреляционная функция разнесения частоты; это Фурье-образ S(). Функция представляет корреляцию между реакциями канала на два сигнала как функцию разности частот этих сигналов. Ее можно рассматривать так, как частотную передаточную функцию канала. Следовательно, расширение сигнала во времени можно рассматривать как следствие процесса фильтрации. Зная , можно определить, какова корреляция между полученными сигналами, разнесенными по частоте на . Функцию можно измерить, передавая пару синусоид, разнесенных по частоте на , изучая взаимную корреляцию спектров двух полученных сигналов и повторяя этот процесс многократно посредством увеличения . Таким образом, измерение можно проводить с помощью синусоид, смещающихся по частоте вдоль интересующей полосы (широкополосный сигнал). Полоса когерентности (coherence bandwidth) f0 является статистической мерой диапазона частот, по которому канал пропускает все спектральные компоненты с приблизительно равным коэффициентом усиления и линейным изменением фазы. Таким образом, полоса когерентности представляет диапазон частот, в пределах которого частотные компоненты сигнала имеют большую вероятность амплитудной корреляции. Иными словами, на все спектральные компоненты этого диапазона канал влияет одинаково, например, проявляя или не проявляя замирание. Следует отметить, что f0 и Ттвзаимосвязаны (с точностью до постоянного множителя). Можно сказать, что приблизительно

f0 = 1/ Tm (15.16)

Максимальная избыточная задержка Ттне обязательно является наилучшим показателем того, как будет функционировать произвольная система при распространении сигнала в канале, поскольку различные каналы с одинаковым значением Тm могут иметь весьма различный профиль интенсивности сигнала в период задержки. Более подходящим параметром является разброс задержек, который чаще всего описывается через среднеквадратическое значение и называется среднеквадратическим разбросом задержек.

(15.17)

Здесь - это средняя избыточная задержка, - квадрат среднего, - второй момент, а - квадратный корень второго центрального момента S() [1].

Не существует универсального соотношения между полосой когерентности и разбросом задержек. Однако, используя метод Фурье-преобразований и измерения дисперсии реальных сигналов в различных каналах, можно получить полезную аппроксимацию. В настоящее время разработано несколько приблизительных соотношений. Если полоса когерентности определена как интервал частот, в пределах которого комплексная частотная передаточная функция канала имеет корреляцию не менее 0,9, то полосу когерентности можно приблизительно записать в следующем виде [16].

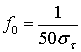(15.18)

Для мобильной радиосвязи в качестве подходящей модели описания распространения в городской среде обычно берут совокупность рассеивающих элементов, имеющих радиальное равномерное распределение, равные коэффициенты отражения, но независимые случайные фазовые углы отражения [17, 18]. Эту модель называют моделью канала с плотным размещением рассеивающих элементов. При ее использовании полоса когерентности частот определяется подобным образом [17]: интервал частот, в пределах которого комплексная частотная передаточная функция канала имеет корреляцию не менее 0,5.

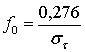(15.19)

При изучении ионосферных эффектов часто используют следующее определение [19].

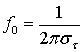(15.20)

Более распространенным приближением для f0, соответствующим определению, где корреляция должна быть не меньше 0,5, является следующее [1].

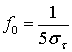(15.21)

Разброс задержек и полоса когерентности связаны с характеристиками многолучевого распространения в канале и отличаются для разных путей распространения (городская черта, пригород, холмистая местность, помещения и т.д.). Важно отметить, что параметры в уравнении (15.21) не зависят от скорости передачи сигналов. Скорость передачи влияет только на ширину полосы пропускания, W.

15.3.2.1. Категории ухудшения качества передачи вследствие расширения сигнала во времени, рассматриваемого в частотной области

Канал называется частотно-селективным (frequency-selective), если f0<1/TS = W, где скорость передачи символов 1/Тs номинально берется равной скорости передачи сигналов или ширине полосы частот сигнала W. На практике W может отличаться от 1/Ts из-за системной фильтрации или выбора типа модуляции данных (например, QPSK, MSK, расширение спектра и т.д.) [20]. Частотно-селективное замирание проявляется тогда, когда канал неодинаково влияет на разные спектральные компоненты сигнала. Некоторые спектральные компоненты сигнала, не входящие в полосу когерентности, будут подвергаться различному (и независимому) воздействию, в отличие от тех компонентов, которые приходятся на полосу когерентности. На рис. 15.9 приведено три примера. В каждом из них показана зависимость спектральной плотности от частоты переданного сигнала, имеющего полосу W Гц. На графике (рис. 15.9, а) на сигнал наложена частотная передаточная функция частотно-селективного канала (f0<W). На рис. 15.9, а показано, что различные спектральные компоненты переданного сигнала будут подвергаться различному воздействию.

Частотно-неселективное, или амплитудное, ухудшение характеристик происходит тогда, когда f0 > W. Следовательно, все спектральные компоненты сигнала будут подвергаться одинаковому воздействию со стороны канала (например, замирать или не замирать). Это показано на рис. 15.9, б, где изображена спектральная плотность того же переданного сигнала, имеющего полосу W Гц.

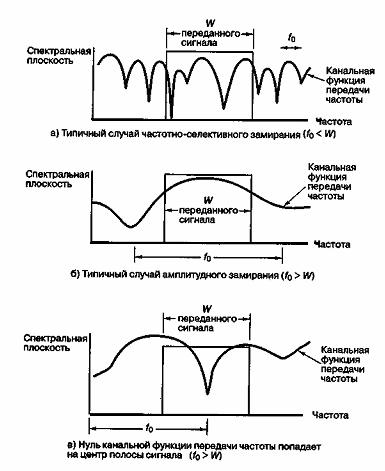
Рис. 15.9. Связь между частотной передаточной функцией канала и переданным сигналом с полосой W

Однако на этот сигнал теперь наложена частотная передаточная функция канала с амплитудным замиранием (f0>W). Из рис. 15.9, б видно, что воздействие на все спектральные компоненты будет приблизительно равным. Амплитудное замирание не привносит искажений, связанных с внесенной каналом ISI, однако все же стоит ожидать ухудшения характеристик сигнала, выражающегося в уменьшении SNR. Чтобы избежать искажения вследствие внесенной каналом ISI, необходимо, чтобы канал проявлял амплитудное замирание. Это происходит при следующем условии.

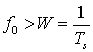(15.22)

Следовательно, полоса когерентности f0 устанавливает верхний предел скорости передачи, которую можно использовать, не включая в приемник эквалайзер.

На рис. 15.9, б показано обычное графическое представление амплитудного замирания, когда f0>W (или Тт<Ts). Однако если мобильный радиоприемник будет менять свое местонахождение, некоторое время получаемый сигнал будет подвергаться частотно-селективному искажению, несмотря на то что f0 > W. Соответствующая иллюстрация приведена на рис. 15.9, в, где нуль частотной передаточной функции канала находится около середины полосы спектральной плотности переданного сигнала. Когда это происходит, узкополосный импульс может искажаться собственными смещенными низкочастотными компонентами. Одним из последствий этого является отсутствие надежного максимума импульса, составляющего основу синхронизации или предназначенного для выборки фазы несущей, переносимой импульсом [17]. Таким образом, хотя канал (на основе среднеквадратических соотношений) отнесен к каналам с амплитудным замиранием, он может периодически проявлять и частотно-селективное замирание. Стоит отметить, что канал мобильной радиосвязи, классифицированный как канал с амплитудным замиранием, не может все время проявлять амплитудное замирание. Когда f0 становится намного больше W (или Тm становится намного меньше Тs), все меньший интервал времени реализуется состояние, показанное на рис. 15.9, в. Очевидно, что замирание на рис. 15.9, а не зависит от места в полосе частот сигнала, так что частотно-селективное замирание происходит не эпизодически, а все время.

15.3.3. Примеры амплитудного и частотно-селективного замирания

На рис. 15.10 показано несколько примеров амплитудного и частотно-селективного замирания для систем со спектром, расширенным методом прямой последовательности (direct-sequence spread-spectrum — DS/SS) [19, 20]. На этом рисунке изображены три графика зависимости выхода коррелятора псевдослучайного (pseudonoise — PN) кода от задержки как функции времени (времени передачи или наблюдения). 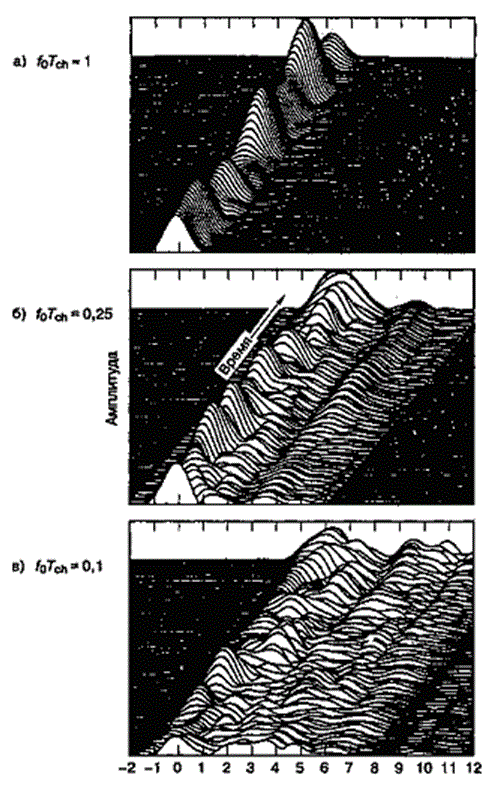Каждый график зависимости амплитуды от задержки подобен зависимости S() от , показанной на рис. 15.8, а. Ключевое различие состоит в том, что амплитуды, показанные на рис. 15.10, представляют выход коррелятора; следовательно, форма сигнала является функцией импульсной характеристики не только канала, но и коррелятора. Задержка выражена в единицах длительности элементарных сигналов, где элементарный сигнал (chip) определяется как минимальный (по длительности) операционный блок системы расширенного спектра. На каждом графике время наблюдения отложено на оси, перпендикулярной плоскости зависимости амплитуды от задержки. Рис. 15.10 составлен по данным канала связи спутник-земля, проявляющего сцинтилляцию вследствие атмосферных помех. В то же время рис. 15.10 является полезной иллюстрацией трех различных состояний канала, которые могут быть применены для мобильной радиосвязи. Как показано на рисунке, на мобильный радиоприемник, движущийся вдоль оси времени наблюдения, влияют изменения профиля многолучевого распространения вдоль маршрута распространения. Ось времени наблюдения проградуирована в единицах элементарных сигналов. На рис. 15.10, а дисперсия сигнала (один пик отраженного сигнала) составляет порядка длительности элементарного сигнала Tch. В типичной системе DS/SS, ширина полосы сигнала расширенного спектра приблизительно равна 1/Tch; таким образом, нормированная полоса когерентности f0Tch на рис. 15.10, а приблизительно равна единице, из чего следует, что ширина полосы когерентности равна порядка ширины полосы расширенного спектра. Это характерно для канала, который можно назвать частотно-неселективным, или слабо частотно-селективным. На рис. 15.10, б, где f0Tch = 0,25, дисперсия сигнала выражена более резко. Существует явно выраженная интерференция между элементарными сигналами, возникающая вследствие того, что ширина полосы когерентности составляет приблизительно 25 процентов от ширины полосы расширенного спектра. На рис. 15.10, в, где f0Tch = 0,1, дисперсия сигнала выражена еще более явно; интерференция между элементарными сигналами возросла вследствие того, что ширина полосы когерентности составляет приблизительно 10 процентов от полосы расширенного спектра. Полосы когерентности (относительно скорости передачи сигнала расширенного спектра), показанные на рис. 15.10, б, в, описывают каналы, которые можно назвать, соответственно, умеренно и сильно селективными по частотам. Позже будет показано, что системы DS/SS, работающие с частотно-селективными каналами на уровне элементарных сигналов, не обязательно испытывают частотно-селективные искажения на уровне символов.

Временная задержка (элементарные сигналы)

Рис. 15.10. Примеры временной развертки выхода согласованного фильтра DS/SS для трех случаев, где Tch— длительность элементарного сигнала. (Источник: Bogusch R. L. "Digital Communications in Fading Channels: Modulation and Coding". Mission Research Corp., Santa Barbara, California, Report no. MRC-R-1034, March, 11, 1987.)

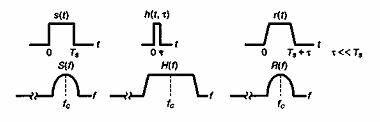
Проявление дисперсии сигнала в каналах с замираниями является аналогом расширения сигнала, характерного для электронного фильтра. На рис. 15.11, а изображен широкополосный фильтр (короткая импульсная характеристика) и его влияние на сигнал во временной и частотной областях. Этот фильтр похож на канал с амплитудным замиранием, выход которого относительно неискажен. На рис. 15.11, б показан узкополосный фильтр (широкая импульсная характеристика). Выходной сигнал претерпевает большее искажение как во временной, так и в частотной области. Данный процесс подобен происходящему в частотно-селективном канале.

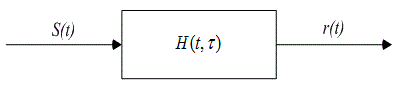
а) Характеристики канала с амплитудным замиранием

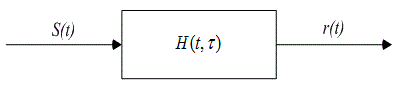
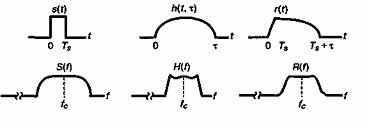
б) Характеристики канала с частотно-селективным замиранием

Рис. 15.11. Характеристики частотно-селективного и амплитудного замирания. (Источник: Rappaport T. S. "Wireless Communications". Prentice-Hall, Upper Saddle River, New Jersey, 1996.)

15.4. Нестационарное поведение канала вследствие движения

15.4.1. Нестационарное поведение канала, рассматриваемое во временной области

Дисперсия сигнала и ширина полосы когерентности описывают в локальной области свойства канала, связанные с расширением во времени. В то же время они не дают информации о переменном во времени поведении канала, являющемся следствием относительного движения передатчика и приемника или передвижения объектов внутри канала. Применяемые в мобильной радиосвязи каналы нестационарны, поскольку движение передатчика и приемника приводит в результате к изменениям пути распространения. Для переданного непрерывного сигнала это вызывает изменения амплитуды и фазы сигнала в приемнике. Если все рассеивающие элементы, составляющие канал, являются стационарными, то при прекращении движения амплитуда и фаза полученного сигнала будут оставаться постоянными, т.е. канал якобы будет стационарным во времени. Как только движение возобновится, поведение канала снова станет переменным во времени. Поскольку характеристики канала зависят от положения передатчика и приемника, переменное во времени поведение в этом случае эквивалентно переменному пространственному поведению.

На рис. 15.8, в показана функция , обозначающая пространственно-временную корреляционную функцию; это автокорреляционная функция отклика канала на поданную синусоиду. Эта функция определяет степень корреляции между откликом канала на синусоиду, отправленную в момент времени t1, и откликом на аналогичную синусоиду, отправленную в момент t2, где . Время когерентности (coherence time) T0 — это мера ожидаемого времени, за которое характеристика канала существенно инвариантна. Ранее измерение дисперсии сигнала и полосы когерентности проводилось с помощью широкополосных сигналов. Теперь для измерения нестационарной природы канала используется узкополосный сигнал [15]. Для измерения можно передать одну и ту же синусоиду () в моменты времени t1 и t2, после чего будет определена функция взаимной корреляции полученных сигналов. Функция и параметр T0 несут в себе информацию о скорости замирания в канале. Отметим, что для идеального стационарного канала (например, передатчик и приемник абсолютно неподвижны) отклик канала будет иметь сильную корреляцию для всех значений ; таким образом, как функция будет постоянной. Например, если расположение стационарного пользователя характеризуется нулем многолучевого распространения, то этот нуль остается неизменным, пока не появится какое-либо движение (либо со стороны передатчика или приемника, либо со стороны объектов на пути распространения). При использовании описанной ранее модели канала с плотным размещением рассеивающих элементов при постоянной скорости перемещения V и немодулированным непрерывным сигналом с длиной волны , нормированная будет иметь следующий вид.

(15.23)

Здесь — функция Бесселя первого рода нулевого порядка [11], Vt — пройденное расстояние, a k = — фазовая постоянная свободного пространства (переводящая расстояние в радианы). Время когерентности можно измерить с помощью времени либо пройденного расстояния (полагая скорость фиксированной). Аморозо (Amoroso) описал такое измерение, используя непрерывный сигнал и модель канала с плотным размещением рассеивающих элементов [17]. Он определил статистическую корреляцию между комбинацией принятой амплитуды и фазы, измеренных при определенном расположении антенны x0, и соответствующей комбинацией амплитуды и фазы, измеренных при несколько смещенном расположении x0 + , причем смещение измерялось в единицах длины волны . Когда смещение между двумя положениями антенны составляет 0,4, совокупные амплитуды и фазы полученного непрерывного сигнала являются статистически некоррелирующими. Иными словами, наблюдение сигнала в точке x0 не дает никакой информации о сигнале в точке x0 + . Отметим также, что при данной скорости это смещение без труда преобразуется во время (время когерентности).

15.4.1.1. Независимость основных проявлений замирания

Для движущейся антенны замирание принятого несущего сигнала обычно рассматривается как случайный процесс, даже если замирание может быть полностью предопределено, исходя из расположения рассеивающих элементов и геометрии распространения между передатчиком и принимающей антенной. Это объясняется тем, что один и тот же сигнал, полученный двумя антеннами, разнесенными, по крайней мере, на 0,4, статистически не коррелирует [17, 18]. Поскольку такие малые расстояния (порядка 13 см для несущей 900 МГц) соответствуют статистической декорреляции принятых сигналов, основные проявления замирания, дисперсия сигнала и скорость замирания, могут рассматриваться независимо друг от друга. Здесь нам может помочь любой из случаев, изображенных на рис. 15.10. В каждый момент времени (соответствующий некоторому пространственному размещению) видим профиль интенсивности многолучевого распространения S() как функцию задержки . Профили многолучевого распространения изначально определяются местностью (строения, растительность и т.д.). Рассмотрим рис. 15.10, б, где стрелочкой, помеченной время (можно было также пометить как смещение антенны), указано направление движения через области с различными профилями многолучевого распространения. При движении мобильного радиопередатчика к новому пространственному положению, которое характеризуется иным профилем, будут происходить изменения в состоянии замирания канала, как обуславливает профиль в новом местоположении. Однако вследствие того, что один профиль декоррелирует с другим уже на расстоянии порядка 13 см (для несущей 900 МГц), скорость таких изменений зависит только от скорости движения, но не от общей геометрии местности.

15.4.1.2. Понятие дуальности

Математическому понятию дуальности (duality) можно дать следующее определение: два процесса (функции, элемента или системы) дуальны друг другу, если математические соотношения между ними остаются неизменными с точностью до замены параметров. В этой главе интересно отметить дуальность при изучении соотношений во временной области по сравнению с соотношениями в частотной области.

Из рис. 15.8 можно определить функции, которые ведут себя одинаково в разных областях. Для понимания модели канала с замираниями рассмотрим дуальные функции (duals). Например, явление дисперсии сигнала можно описать в частотной области с помощью функции , как это показано на рис. 15.8, б. Эта функция несет в себе информацию о диапазоне частот, в котором два спектральных компонента полученного сигнала имеют большую вероятность амплитудной и частотной корреляции. Скорость замирания во временной области описывается функцией , как это показано на рис. 15.8, в. Эта функция несет в себе информацию об интервале времени, в течение которого два полученных сигнала имеют большую вероятность амплитудной и фазовой корреляции. На рисунке эти две корреляционные функции, и , помечены как дуальные. Это отмечено также на рис. 15.1, где дуальными названы блоки 10 и 13, и на рис. 15.7, где дуальны механизм расширения во времени в частотной области и механизм нестационарности во временной области.

15.4.1.3. Категории ухудшения качества передачи вследствие нестационарного поведения канала, рассматриваемого во временной области

Нестационарную природу, или механизм скорости замирания в канале, можно рассматривать с позиции категорий ухудшения качества передачи, указанных на рис. 15.7, — быстрого и медленного замирания. Термин "быстрое замирание" (fast fading) используется для описания каналов, в которых Т0 < Ts, где Т0 — время когерентности канала, а Ts — длительность символа. Быстрое замирание описывает условие, когда временной интервал, в течение которого поведение канала имеет корреляционный характер, мал по сравнению со временем, необходимым для передачи символа. Таким образом, можно ожидать, что характер замирания в канале будет изменяться несколько раз за время передачи символа, что приведет к искажению вида узкополосного импульса. Данное искажение аналогично описанному ранее, которое вызывается внесенной каналом ISI, поскольку принятые компоненты сигнала не сильно коррелируют во времени. Поэтому быстрое замирание может искажать узкополосный импульс, что, как правило, приводит к частому появлению неустранимых ошибок. Такие искаженные импульсы вызывают проблемы синхронизации (сбои в работе приемников, использующих фазовую автоподстройку частоты). Кроме того, существуют трудности, связанные с адекватной разработкой согласованного фильтра.

Обычно говорят, что канал вносит медленное замирание (slow fading), если Т0 > Ts. Здесь временной интервал, в течение которого поведение канала имеет корреляционный характер, велик по сравнению со временем, необходимым для передачи символа. Следовательно, можно ожидать, что состояние канала будет оставаться практически неизменным в течение времени передачи символа. Распространяющиеся символы, вероятнее всего, не пострадают в результате искажений импульса, описанных ранее. Основное ухудшение качества передачи в канале с медленным замиранием, как и в случае с амплитудным замиранием, связано с уменьшением SNR.

15.4.2. Нестационарное поведение канала, рассматриваемое в области доплеровского сдвига

Аналогично характеристика нестационарной природы канала может быть представлена в области доплеровского сдвига (частот). На рис. 15.8, г показана доплеровская спектральная плотность мощности (или доплеровский спектр) S(v), изображенная в виде функции от доплеровского сдвига частот. Для модели с плотным размещением рассеивающих элементов, вертикальной принимающей антенной с постоянным азимутальным усилением, однородным угловым распределением входящего сигнала по всем углам в интервале (0, 2) и немодулированным непрерывным сигналом спектр сигнала в точках приема будет иметь следующий вид.

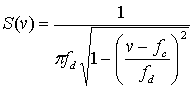(15.24)

Равенство сохраняется для сдвига частот v, находящегося в интервале в окрестности несущей частоты ; за пределами этого интервала оно обращается в нуль. Профиль радиочастотного доплеровского спектра, который описывается уравнением (15.24), имеет классическую форму чаши, что видно из рис. 15.8, г. Следует заметить, что профиль спектра является результатом принятия модели канала с плотным размещением рассеивающих элементов. Уравнение (15.24) было введено для согласования экспериментальных данных, собранных для каналов мобильной радиосвязи [22]; однако для разных приложений профили спектра различны. Например, модель с плотным размещением рассеивающих элементов несправедлива для каналов радиосвязи внутри помещений; модель канала для областей внутри помещения предполагает, что S(v) является равномерным спектром [23].

На рис. 15.8, г заостренность и крутизна границ спектра доплеровских частот является следствием резкого верхнего предела доплеровского сдвига, вызванного перемещением передвижной антенны среди стационарных рассеивающих элементов в модели плотного размещения. Наибольшая величина (бесконечность) S(v) соответствует случаю, когда рассеивающий элемент находится прямо перед движущейся платформой антенны или прямо позади нее. В этом случае величина сдвига частот описывается формулой

(15.25)

где V — относительная скорость, а — длина волны сигнала. Если передатчик и приемник движутся навстречу друг другу, то fd положительна, а если они удаляются друг от друга, то fd отрицательна. Что касается рассеивающих элементов, находящихся в направлении поперечного излучения движущейся платформы, то для них величина частотного сдвига равна нулю. Отметим, что хотя доплеровские компоненты, поступившие точно под углами 0° и 180°, имеют бесконечно большую спектральную плотность мощности, это не представляет проблемы, поскольку угол имеет непрерывное распределение, а вероятность поступления компонентов точно под этими углами равна нулю [1, 18].

S(v) является Фурье-образом R(t). Известно, что Фурье-образ автокорреляционной функции временного ряда равен квадрату амплитуды Фурье-образа исходного временного ряда. Следовательно, измерения могут проводиться просто путем передачи синусоиды (узкополосный сигнал) и с использованием Фурье-анализа для получения спектра мощности полученной амплитуды [15]. Этот доплеровский спектр мощности канала дает информацию о спектральном расширении переданной синусоиды (импульса в частотной области) в области доплеровского сдвига. Как показано на рис. 15.8, функцию S(v) можно рассматривать как дуальную профилю интенсивности многолучевого распространения , поскольку последняя несет информацию о расширении во времени переданного импульса в области задержки. Это также отмечено на рис. 15.1 в виде дуальности между блоками 7 и 16, а на рис. 15.7 — между механизмом расширения во времени в области задержки и механизмом нестационарного поведения канала в области доплеровского смещения.

Знание S(v) делает возможным приблизительное вычисление величины расширения спектра как функции скорости изменения состояний канала. Ширина доплеровского спектра мощности (обозначенная fd) в литературе называется по-разному: доплеровское расширение (Doppler spread), скорость замирания (fading rate), ширина полосы замирания (fading bandwidth) или спектральное расширение (spectral broadering). Уравнение (15.25) описывает доплеровский сдвиг частоты. В обычной для многолучевого распространения окружающей среде полученный сигнал движется по нескольким отраженным путям, каждый из которых имеет отличные от других расстояние и угол поступления. Доплеровский сдвиг для каждого из путей поступления сигнала, как правило, различен. Воздействие на полученный сигнал, как правило, проявляется в виде доплеровского расширения переданной частоты сигнала, а не как сдвиг. Нужно помнить, что доплеровское расширение fd и время когерентности Т0обратно пропорциональны (с точностью до постоянного множителя), что позволяет записать следующее приблизительное соотношение между этими двумя параметрами.

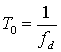(15.26)

Поэтому доплеровское расширение fd (или 1/T0) рассматривается как обычная скорость замирания в канале. Ранее Т0определялся как ожидаемый интервал времени, в течение которого отклик канала на синусоиду существенно инвариантен. Если Т0определять более точно, как интервал времени, в течение которого отклики канала на синусоиды имеют между собой корреляцию не менее 0,5, соотношение между Т0и fd будет приблизительно следующим.

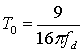(15.27)

Известным эмпирическим правилом является определение Т0через геометрическое среднее уравнений (15.26) и (15.27). Это приводит к следующему.

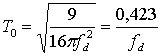(15.28)

Для мобильной радиосвязи на частоте 900 МГц, на рис. 15.12 показано типичное влияние релеевского замирания на огибающую амплитуды сигнала в зависимости от времени [1]. На рисунке показано, что расстояние, пройденное мобильным аппаратом за интервал времени, соответствующий двум соседним нулям (мелкомасштабное замирание), равно по порядку половине длины волны (/2). Таким образом, из рис. 15.12 и уравнения (15.25) ясно, что время, требуемое для прохождения расстояния /2 (равное приблизительно времени когерентности) при движении с постоянной скоростью V, будет следующим.

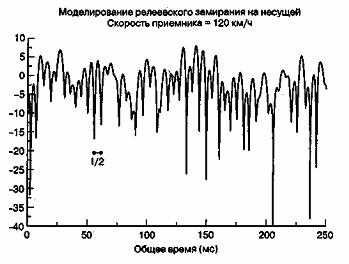
Рис. 15.12. Типичный профиль огибающей при релеевском замирании на частоте 900 МГц. (Rappaport T. S. Wireless Communications. Chapter 4, Prentice-Hall, Upper Saddle River, New Jersey, 1996.)

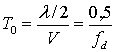(15.29)

Таким образом, когда расстояние между периодами замирания приблизительно равно , как показано на рис. 15.12, результирующее выражение для Т0в уравнении (15.29) близко к геометрическому среднему, показанному в уравнении (15.28). Из уравнения (15.29), используя параметры, показанные на рис. 15.12 (скорость — 120 км/ч, несущая частота — 900 МГц), можно получить, что время когерентности канала — приблизительно 5 мс, а доплеровское расширение (скорость замирания в канале) — приблизительно 100 Гц. Следовательно, если в этом примере представлен канал, по которому передается оцифрованная речь с типичной скоростью 10⁴ символов/с, скорость замирания значительно меньше скорости передачи символов. При таких условиях канал будет проявлять эффекты медленного замирания. Нужно сказать, что если бы абсцисса на рис. 15.12 была проградуирована в единицах длины волны, а не в единицах времени, то отображенные характеристики замирания выглядели бы так же для любой радиочастоты и любой скорости движения антенны.

15.4.2.1. Аналогия спектрального расширения в каналах с замираниями

Рассмотрим причину, по которой сигнал испытывает спектральное расширение при распространении или приеме подвижной платформой, и то, почему спектральное расширение (называемое также скоростью замирания в канале) является функцией скорости движения. Для объяснения этого явления можно воспользоваться следующей аналогией. На рис. 15.13 показана манипуляция цифровым сигналом (такая, как амплитудная или частотная манипуляция), где тон cos, определенный в интервале , характеризуется в частотной области импульсами (). Такое представление в частотной области является идеальным (т.е. нулевая ширина полосы частот), поскольку тон — это одна частота с бесконечной длительностью. В практических приложениях при передаче цифрового сигнала происходит включение и выключение (манипуляция) сигналов с требуемой скоростью. Манипуляция может рассматриваться как умножение тона бесконечной длительности на рис. 15.13, а на идеально прямоугольную функцию манипуляции (коммутации) на рис. 15.13, б. Описание такой коммутационной функции в частотной области имеет вид sinс fT (см. приложение А, табл. А. 1).

На рис. 15.13, в показан полученный в результате умножения тон cos, теперь ограниченный по длительности. Результирующий спектр получается путем свертки спектральных импульсов (рис. 15.13, а) с функцией sinс fT (рис. 15.13, б); этот результирующий расширенный спектр показан на 15.13, в. Далее видно, что если передача сигналов происходит с более высокой скоростью, которой соответствует прямоугольник меньшей длины (рис. 15.13, г), то для результирующего спектра сигнала (рис. 15.13, д) характерно большее расширение спектра. Изменение состояния канала с замиранием является в какой-то мере аналогом амплитудной модуляции цифровых сигналов. Канал ведет себя как коммутатор, "включающий и выключающий" сигнал. Чем выше скорость изменения состояния канала, тем большее расширение спектра испытывает сигнал, распространяющийся по такому каналу. Это неточная аналогия, поскольку включение и выключение сигналов может привести к разрыву фазы, в то время как для типичных рассеивающих элементов при многолучевом распространении характерна непрерывность фазы.

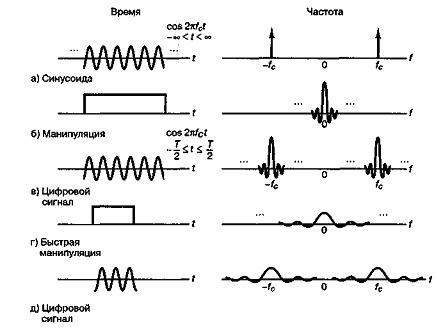
Рис. 15.13. Аналогия между расширением спектра при замирании и расширением спектра при манипуляции цифровым сигналом

15.4.2.2. Категории ухудшения характеристик вследствие нестационарной природы канала, рассматриваемые в области доплеровского сдвига

Говорят, что в канале имеет место быстрое замирание, если скорость передачи символов 1/Ts, (приблизительно равная скорости передачи сигналов или ширине полосы частот W) меньше скорости замирания 1/T0 (приблизительно равной fd), т.е. быстрое замирание характеризуется следующими соотношениями.

W<fd (15.30)

или

Тs >Т0 (15.31)

Наоборот, в канале имеет место медленное замирание, если скорость передачи сигналов больше скорости замирания. Таким образом, чтобы избежать искажения сигнала, вызванного быстрым замиранием, нужно создать канал, который будет подвержен медленному замиранию, что обеспечивается за счет большей скорости передачи сигнала по сравнению со скоростью замирания.

W > fd (15.32)

или

Ts < T0 (15.33)

В уравнении (15.22) показано, что вследствие дисперсии сигнала ширина полосы когерентности f0 устанавливает верхний предел скорости передачи сигналов, при которой отсутствует частотно-селективное искажение. Аналогично в уравнении (15.32) показано, что в результате доплеровского расширения скорость замирания в канале fd устанавливает нижний предел скорости передачи сигнала, при которой отсутствует искажение, связанное с быстрым замиранием. Для систем связи высоких частот, если телетайпное сообщение или сообщение в азбуке Морзе было передано с низкой скоростью передачи данных, в каналах часто наблюдаются характерные особенности быстрого замирания. В то же время большинство современных наземных каналов мобильной радиосвязи чаще всего можно охарактеризовать как каналы с медленным замиранием.

Уравнений (15.32) и (15.33) недостаточно для описания желаемого поведения канала. Лучшим способом задания требований для избежания быстрого замирания было бы условие (или ). Если это условие не удовлетворено, то случайная частотная модуляция (frequency modulation — FM), вызванная переменными доплеровскими сдвигами, будет существенно ухудшать характеристики системы. Эффект Доплера приводит к частому появлению неустранимых ошибок, которые нельзя компенсировать простым увеличением [24]. Это частое появление неустранимых ошибок наиболее резко выражено во всевозможных схемах передачи, использующих модуляцию несущей фазы. Отдельный отраженный доплеровский путь (без рассеивающих элементов) регистрирует мгновенный сдвиг, традиционно вычисляемый как . Однако комбинация отраженных и многолучевых компонентов порождает довольно сложную временного зависимость мгновенной частоты, которая может вызвать колебания частоты, сильно превышающие при восстановлении информации детектором мгновенной частоты (который является нелинейным устройством) [25]. На рис. 15.14 показано, как это происходит. В результате движения переносного устройства в момент времени t1 отраженный вектор поворачивается на угол , в то время как суммарный вектор поворачивается на угол , который приблизительно в четыре раза больше . Скорость изменения фазы в момент времени, близкий к этому конкретному периоду замирания, приблизительно равна скорости изменения отраженной доплеровской фазы, умноженной на 4. Следовательно, сдвиг мгновенной частоты был бы в 4 раза больше отраженного доплеровского сдвига. Образование резких максимумов мгновенных сдвигов частот в моменты времени, близкие к сильному замиранию, подобно появлению "щелчков" или "пиков", характерных для сигнала FM. На рис. 15.15 продемонстрирована серьезность этой проблемы. На рисунке показан график зависимости частоты появления однобитовых ошибок от для передачи сигнала с модуляцией DQPSK на частоте f0 = 850 МГц для различных моделируемых скоростей переносного устройства [26]. Должно быть ясно, что при высоких скоростях кривая характеристики спускается до уровня частоты появления ошибок, который может быть недопустимо высок. В идеале, когерентный демодулятор, который захватывает и отслеживает информационный сигнал, должен был бы гасить влияние такого шума частотной модуляции, таким образом, исключая влияние доплеровского сдвига. Однако при больших значениях fd восстановление несущей реализовать сложно, поскольку нужно построить очень широкополосные (по отношению к скорости передачи данных) схемы фазовой автоподстройки частоты (phase-lock loop — PLL, ФАПЧ). Для приложений речевой связи с частотой появления ошибок в интервале от 10^-3 до 10^-4 учитывается большое значение доплеровского сдвига, которое считается равным по порядку величине 0,01W. Следовательно, во избежание искажений, вызванных быстрым замиранием, и частого появления неустранимых ошибок, вызванных эффектом Доплера, скорость передачи сигнала должна превышать скорость замирания в 100-200 раз [27]. Точное значение зависит от типа модуляции сигнала, строения приемника и требуемой частоты появления ошибок [1, 25-29]. Девериан (Davarian) [29] показал, что система, отслеживающая частоту, может посредством дифференциальной манипуляции с минимальным сдвигом (differential minimum-shift keying — DMSK) снизить (но не устранить) частоту появления неустранимых ошибок в мобильных системах связи.

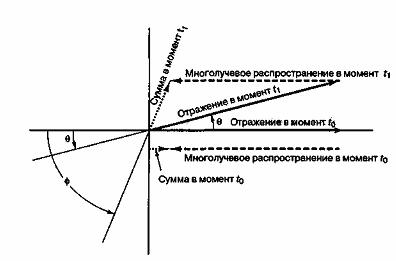
Рис. 15.14. Комбинация отраженного и многолучевого компонентов может давать большее колебание частоты, чем . (Источник: Amoroso F. Instantaneous Frequency Effects in a Doppler Scattering Environment. IEEE International Conference on Communications, June 7—10, 1987, pp. 1458-1466.)

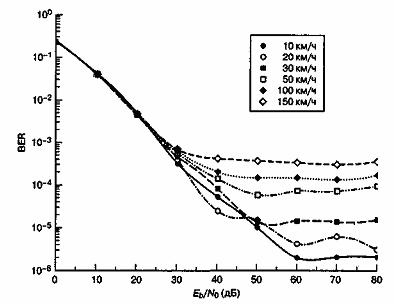
Рис. 15.15. Зависимость вероятности частоты появления ошибки от для схемы DQPSK при разных скоростях движения: fc = 850 МГц, Rs = символов/с. (Источник: Fung V., Rappaport T. S. and Thoma В. Bit-Error Simulation for x/4 DQPSK Mobile Radio Communication Using Two-Ray and Measurement-Based Impulse Response Models. IEEE Journal on Selected Areas in Communication, Vol. 11, n. 3, April, 1993, pp. 393-405.)

15.4.3. Релеевский канал с медленным и амплитудным замиранием

При дискретном многолучевом канале с комплексной огибающей g(t), описываемой уравнением (15.3), демодулированный сигнал (шумом пренебрегаем) описывается уравнением (15.10), которое повторно приводится ниже.

(15.34, а)

Здесь R(t) = |g(t)| — модуль огибающей, а — ее фаза. Предположим, что канал проявляет амплитудное замирание, так что многолучевые компоненты не разрешаются. Тогда слагаемые {} в уравнении (15.34, а) за один период передачи сигнала Т нужно выразить как результирующую амплитуду всех п векторов, полученных за этот промежуток времени. Аналогично фазовые члены в уравнении (15.34, а) за один период передачи сигнала нужно выразить как результирующую фазу всех и замирающих векторов плюс информационную фазу, полученную за этот промежуток. Пусть канал проявляет медленное замирание, так что с помощью применения контура фазовой автоподстройки частоты (phase-lock loop — PLL, ФАПЧ) или другого подходящего метода фазу (с незначительной погрешностью) можно вычислить из полученного сигнала. Следовательно, в канале с медленным и амплитудным замиранием для каждого периода передачи сигнала можно записать включающую шум п0 (Т) тестовую статистику вне демодулятора.

(15.34, б)

Далее для простоты вместо будем писать . При двоичной передаче по каналу AWGN с фиксированным коэффициентом замирания = 1 вероятность появления битовой ошибки для основной когерентной и некогерентной схем PSK и ортогональной схемы FSK представлена в главе 4, табл. 4.1. Все графики зависимости вероятности появления ошибочного бита от Eb /N0 для таких схем передачи сигнала показывают классическую экспоненциальную зависимость ("водопадоподобный" вид, ассоциируемый с каналом AWGN). Однако, при условии многолучевого распространения, если отсутствует отраженный компонент сигнала, является случайной переменной с релеевским распределением; или, что равнозначно, ² описывается плотностью вероятности . На рис. 15.16 отображен график вероятности ошибки для такого релеевского замирания. Если Е(²)>>1, где Е выражает математическое ожидание, то формулы для вероятности битовой ошибки при использовании основных схем двоичной передачи сигналов, показанных на рис. 15.16, даны в табл. 15.1. Каждая схема передачи сигнала, которая в канале AWGN давала график в виде водопада, представленный на рис. 4.25, теперь, в результате релеевского замирания, описывается приблизительно линейной функцией.

Таблица 15.1. Релеевская граничная вероятность битовой ошибки (где Е(²)>>1)

Модуляция	РВ
PSK (когерентная)
DPSK (дифференциально-когерентная)
Ортогональная FSK (когерентная)
Ортогональная FSK (некогерентная)

Proakis J. D. Digital Communications. McGraw-Hill, New York, 1983.

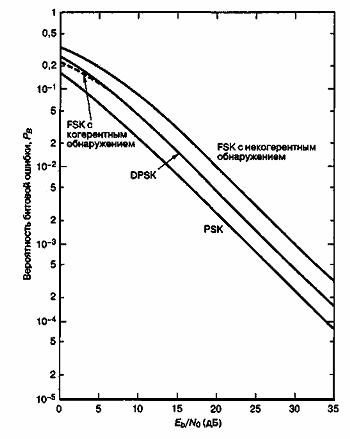
Рис. 15.16. Вероятность ошибки при двоичной передаче по каналу с медленным релеевским замиранием. (Источник: Proakis J. G. Digital Communications, McGraw-Hill Book Company, New York, 1983.)

15.5. Борьба с ухудшением характеристик, вызванным эффектами замирания

В подписи к рис. 15.17 "хорошая, плохая, ужасная" отражены три основные категории характеристик, выраженных через вероятность битовой ошибки в зависимости от . Крайняя левая кривая, имеющая экспоненциальную форму, соответствует ожидаемому поведению данной зависимости при использовании любых номинальных схем модуляции при AWGN. Видно, что при разумном уровне можно ожидать хорошей достоверности передачи. Средняя кривая, названная релеевским пределом, демонстрирует ухудшение достоверности передачи, вытекающее из уменьшения , что характерно для амплитудного или медленного замирания при отсутствии компонента, распространяющегося вдоль линии прямой видимости. Кривая является функцией, обратно пропорциональной , так что для значений , представляющих практический интерес, характеристики будут «плохими». При релеевском замирании, чтобы указать на то, что проводится усреднение по «лучшим» и «худшим» случаям замирания, часто вводятся параметры с чертой. Следовательно, часто можно увидеть графики вероятности битовой ошибки с усредненными параметрами, обозначенными и . Такое обозначение акцентирует внимание на том, что каналы с замираниями имеют память; таким образом, принятые выборки сигнала коррелируют друг с другом во времени. Следовательно, при создании таких графиков вероятности ошибки для каналов с замиранием, необходимо изучить процесс в течение промежутка времени, намного превышающего время когерентности канала. Кривая, достигающая непоправимого уровня ошибок, часто называется дном ошибок (error floor) и представляет «ужасную» характеристику, при этом вероятность битовой ошибки может выходить на постоянный уровень, близкий к 0,5. Это соответствует эффекту сильного ухудшения характеристик, который может проявиться при частотно-селективном или быстром замирании.

Если в результате замирания канал вносит искажения в сигнал, для системы может быть характерен неисправимый уровень ошибок, превышающий допустимую частоту появления ошибок. В этом случае никакое увеличение не поможет достичь желаемого уровня достоверности передачи, и единственно доступным подходом, допускающим улучшение, является использование каких-либо иных методов устранения или уменьшения искажений. Метод борьбы зависит от того, вызвано ли искажение частотно-селективным или быстрым замиранием. Когда искажение сигнала будет смягчено, зависимость РВот может перейти из категории «ужасно» в категорию, близкую к «плохо» — кривая релеевского предела. Далее можно использовать дополнительные методы борьбы с эффектами, вызванными замиранием, приложив усилия к приближению характеристики системы к характеристикам канала AWGN, применив некоторые виды разнесения, чтобы снабдить приемник набором некоррелирующих копий сигнала, и воспользовавшись мощным кодом коррекции ошибок.

На рис. 15.18 перечислено несколько методов борьбы как с искажением сигнала, так и с уменьшением SNR. Если рис. 15.1 и 15.7 играют роль проводника по описанию явлений замирания и их следствий, то рис. 15.18 аналогичным образом может служить для описания методов борьбы с этими явлениями и их следствиями. Предлагаемые подходы используются, когда проектирование системы рассматривается в два основных этапа: первый — выбор метода борьбы, уменьшающего или устраняющего любые ухудшения характеристик, вызванные искажениями; второй — выбор типа разнесения, который позволил бы наилучшим образом приблизиться к характеристикам канала AWGN.

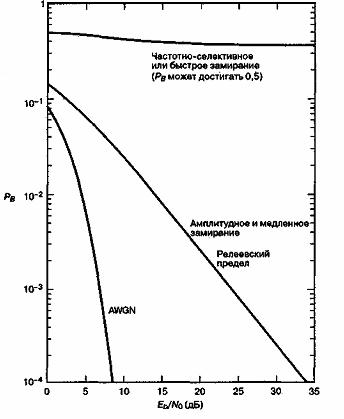
Рис. 15.17. Достоверность передачи сигналов: хорошая, плохая, ужасная

Рис. 15.18. Основные типы борьбы с искажениями и снижением SNR

15.5.1. Борьба с частотно-селективными искажениями

Для борьбы с вызванной каналом ISI, которая возникает вследствие частотно-селективного замирания, может использоваться выравнивание. Иными словами, выравнивание изменяет характеристики системы, описываемые кривой, которая на рис. 15.17 названа «ужасно», на характеристики, близкие к кривой «плохо». Процесс выравнивания для уменьшения воздействия ISI заключается в использовании методов, собирающих рассеянную энергию символа в ее исходный временной интервал. По сути, эквалайзер (устройство выравнивания) является обратным фильтром канала. Если канал является частотно-селективным, эквалайзер усиливает частотные Компоненты с малыми амплитудами и ослабляет с большими. Целью комбинации канала и выравнивающего фильтра является получение плоской частотной характеристики и линейного изменения фазы [30]. Поскольку в мобильных системах характеристика канала меняется со временем, выравнивающий фильтр должен изменяться или приспосабливаться к нестационарным характеристикам канала. Следовательно, такие фильтры являются адаптивными устройствами, которые предназначены не только для борьбы с искажениями; они также обеспечивают разнесение. Поскольку ослабление искажений выполняется путем сбора рассеянной энергии символа в исходный временной интервал символа (так, чтобы это не мешало обнаружению других символов), эквалайзер попутно предоставляет приемнику энергию символа, которая в противном случае была бы утрачена.

Эквалайзер с обратной связью по решению (decision feedback equalizer — DFE) имеет участок прямой связи, являющийся линейным трансверсальным фильтром [30], размер регистра и весовые коэффициенты отводов которого выбраны так, чтобы когерентно собирать практически всю энергию текущего символа. Эквалайзер DFE имеет также участок обратной связи, который удаляет энергию, оставшуюся от ранее обнаруженных символов [10, 30-32]. Принцип работы DFE основан на следующем: когда обнаруживается информационный символ, ISI, вносимая им в последующие символы, может быть оценена и вычтена до обнаружения последующих символов (см. раздел 3.4.3.2.).

Эквалайзер, работающий по принципу оценки последовательности с максимальным правдоподобием (maximum-likelihood sequence estimation — MLSE), проверяет все возможные последовательности данных (вместо того чтобы обнаруживать каждый полученный символ отдельно) и выбирает ту, которая является наиболее вероятной из всех кандидатов. Эквалайзер MLSE впервые был предложен Форни (Forney) [33] и реализован с использованием алгоритма декодирования Витерби [34]. Принцип MLSE оптимален в том смысле, что он минимизирует вероятность ошибки последовательности. Поскольку при реализации эквалайзера MLSE обычно используется алгоритм декодирования Витерби, это устройство часто называют эквалайзером Витерби (Viterbi equalizer). Позже в этой главе будет продемонстрировано адаптивное выравнивание, применяемое в системе GSM (Global System for Mobile — глобальная система мобильной связи), где используется эквалайзер Витерби.

Расширение спектра методом прямой последовательности (direct-sequence spread-spectrum — DS/SS) может использоваться для уменьшения искажений, вызванных частотно-селективной ISI, поскольку отличительной особенностью систем расширенного спектра является их способность отфильтровывать помехи, a ISI — это один из видов помех. Рассмотрим систему DS/SS, в которой используется двоичная фазовая манипуляция (binary phase-shift keying — BPSK) и канал связи, содержащий один прямой и один отраженный путь. Пусть распространение от передатчика к приемнику приводит к многолучевому распространению сигнала, запаздывающего на по сравнению с прямым сигналом. Пренебрегая шумом, многолучевой сигнал можно выразить следующим образом.

(15.35)

Здесь x(t) — информационный сигнал, g(t) — шумоподобный (pseudonoise — PN) код расширения, — разность во времени распространения между двумя путями, а — поглощение многолучевого сигнала по сравнению с сигналом, распространяющимся по прямому пути. Кроме того, предполагается, что случайная фаза в равномерно распределена в интервале (0,2), Приемник умножает поступающий сигнал r(t) на код g(t). Если приемник синхронизирован с сигналом, распространяющимся по прямому пути, умножение на кодовый сигнал дает следующее.

(15.36)

где g²(t) = 1. Если больше длительности элементарного псевдошумового сигнала, тогда

(15.37)

по некоторому удобному интервалу интегрирования (корреляция). Таким образом, система расширенного спектра эффективно устраняет многолучевую интерференцию за счет корреляционного (по коду) приемника. Хотя наличие введенной каналом ISI обычно не заметно для систем DS/SS, такие системы подвержены потерям энергии, содержащейся в многолучевых компонентах, отклоняемых приемником. Необходимость сбора утраченной энергии, принадлежащей подобным многолучевым элементарным сигналам, стала причиной разработки RAKE-приемника (RAKE receiver) [35-37]. В этом приемнике каждому многолучевому компоненту выделяется отдельный коррелятор. Приемник когерентно суммирует энергию каждого луча, избирательно задерживая их (более ранние компоненты задерживаются дольше) таким образом, чтобы они объединялись когерентно.

Ранее описывался канал, который можно классифицировать как канал с амплитудным замиранием, но который время от времени (когда нуль частотной передаточной функции канала попадает на центр полосы сигнала) проявляет частотно-селективное искажение. Использование DS/SS является удобным методом борьбы с таким искажением, поскольку широкополосный сигнал SS может охватить большое число периодов характеристики частотно-селективного ослабления. Таким образом, большая часть энергии импульса пройдет через среду рассеивающих элементов, что отличается от воздействия нулей канала на узкополосный сигнал [17] (см. рис. 15.9, в). Способность спектра сигнала охватывать, большое число периодов передаточной функции частотно-селективного канала является ключевой, позволяющей сигналу DS/SS преодолевать искажающее влияние многолучевой среды. Необходимое условие: ширина полосы частот расширенного спектра Wss (или скорость передачи элементарных сигналов Rch) должна быть больше ширины полосы когерентности f0. Чем больше отношение Wss к f0, тем более эффективным будет подавление искажений. Временное представление такого подавления выражено в уравнениях (15.36) и (15.37). Таким образом, чтобы разрешить многолучевые компоненты (либо отбросить их, либо использовать в RAKE-приемнике), необходимо, чтобы дисперсия сигнала расширенного спектра была больше скорости передачи элементарных сигналов.

Расширение спектра методом скачкообразной перестройки частоты (frequency hopping spread spectrum - FH/SS) может использоваться для борьбы с искажениями, вызванными частотно-селективным замиранием, причем скорость изменения частоты должна быть не меньше скорости передачи символов. Ослабление искажений происходит в данном случае благодаря механизмам, отличным от использованных в DS/SS. Приемники с перестройкой частоты избегают эффектов искажения вследствие многолучевого распространения, быстро меняя в передатчике полосу несущей Частоты; таким образом, помехи не возникают, поскольку изменение положения полосы частот приемника происходит до поступления многолучевого сигнала.

Ортогональное уплотнение с частотным разделением (orthogonal frequency-division multiplexing - OFDM) может использоваться при передаче сигнала в каналах с частотно-селективным замиранием для увеличения периода передачи символа, что позволит избежать применения эквалайзера. Принцип работы заключается в разделении (разуплотнении) последовательности с высокой скоростью передачи на N групп символов так, чтобы каждая группа содержала последовательность с более низкой скоростью передачи символов (в N раз меньшую), чем у исходной последовательности. Полоса сигнала состоит из N ортогональных несущих сигналов, каждый из которых модулируется отличной от других группой символов. Целью является снижение скорости передачи символов (скорости передачи сигналов) W на каждой несущей так, чтобы она была меньше ширины полосы когерентности канала f0 Метод OFDM, изначально именуемый Kineplex, — это метод, реализованный в мобильных системах радиосвязи США [38] и использованный в Европе под названием кодированное OFDM (Coded OFDM — COFDM) в телевидении высокой четкости (high-definition television — HDTV) [39].

Контрольный сигнал (pilot signal) — это сигнал, способствующий когерентному обнаружению сигналов. Контрольные сигналы можно реализовать в частотной области как внутриполосные тоны [40] или во временной области как цифровые последовательности, которые могут также предоставлять информацию о состоянии канала и таким образом улучшать достоверность передачи при замирании [41].

15.5.2. Борьба с искажениями, вызванными быстрым замиранием

Искажения, вызванные быстрым замиранием, приводят к необходимости использования помехоустойчивой схемы модуляции (некогерентной или дифференциально-когерентной), которая не требует сопровождения фазы и снижает время интеграции детектора [19]. Кроме того, можно увеличить скорость передачи символов W, чтобы она превышала скорость замирания , путем введения избыточности сигнала. Кодирование с коррекцией ошибок может также вносить улучшения; взамен повышения энергии сигнала код снижает требуемое для получения заданной достоверности передачи. При данном при наличии кодирования дно ошибок вне демодулятора не будет опускаться, при этом вне декодера может быть достигнута меньшая частота появления ошибок [19]. Таким образом, при кодировании можно получить приемлемую достоверность передачи и, по сути, допустить более высокий уровень ошибок в сигналах, поступающих от демодулятора, который в противном случае был бы неприемлем. Чтобы воспользоваться преимуществами кодирования, ошибки вне демодулятора должны не коррелировать (что обычно бывает в среде с быстрым замиранием) либо в систему должно внедряться устройство чередования.

Если одновременно происходит ухудшение характеристик в результате быстрого замирания и частотной избирательности, улучшение может обеспечить один интересный метод фильтрации. Частотно-селективное ухудшение характеристик можно снизить, используя набор сигналов с OFDM. В то же время обычные сигналы OFDM искажаются в результате быстрого замирания (доплеровское расширение нарушает ортогональность поднесущих OFDM). В этом случае для формирования сигнала во временной области и кодирования с частичным откликом, (см. раздел 2.9) с целью уменьшения боковых спектральных лепестков набора сигналов (что помогает сохранить их ортогональность) используется метод полифазной фильтрации [24]. Процесс вносит известную ISI и помехи соседнего канала (adjacent channel interference - АСI), которые затем устраняются последующей обработкой на эквалайзере и применением гасящего фильтра [43].

15.5.3. Борьба с уменьшением SNR

После реализации некоторых методов борьбы с ослаблением сигнала вследствие частотно-селективного и быстрого замирания, следующим шагом является использование методов разнесения для перемещения рабочей точки системы с кривой достоверности передачи, помеченной «плохо» на рис. 15.17, на кривую, приближающуюся к характеристике AWGN. Термин «разнесение» (diversity) применяется для обозначения различных методов, пригодных для некоррелированного воспроизведения приемником интересующего сигнала. Некоррелированность является здесь важной особенностью, поскольку дополнительные копии сигнала ничем не помогли бы приемнику, если бы все эти копии были одинаково плохи. Ниже перечислены некоторые способы реализации методов разнесения.

• Разнесение во времени (time diversity) может обеспечиваться путем передачи сигнала в L различных временных интервалах с разнесением не менее чем на Т0. Пример разнесения во времени — чередование, использованное совместно с кодированием с коррекцией ошибок.

• Разнесение по частоте (frequency diversity) может обеспечиваться путем передачи сигнала на L различных несущих с частотным разнесением не менее f0. Пример разнесения по частоте — расширение полосы частот. Полоса частот сигнала W расширяется так, чтобы превышать f0, предоставляя приемнику несколько независимо замирающих копий сигнала. При этом достигается частотное разнесение порядка L = W/f0. Когда W становится большеf0, то, если не используется выравнивание, существует возможность частотно-селективного искажения. Таким образом, расширенная полоса частот может улучшить характеристики системы (посредством разнесения) только в том случае, если ослаблено частотно-селективное искажение, связанное с этим разнесением.

• Системы расширенного спектра (spread-spectrum systems) — это системы, в которых для исключения интерферирующих сигналов используются методы расширения полосы частот. Если спектр расширяется методом прямой последовательности (direct-sequence spread-spectrum — DS/SS), то, как было показано ранее, многолучевые компоненты отбрасываются, если задержка их поступления превышает длительность одного элементарного сигнала. Однако чтобы приблизиться к характеристикам AWGN, необходимо компенсировать потерю энергии, которая содержится в этих отброшенных компонентах. RAKE-приемник (описанный позже) дает возможность когерентно объединять энергию нескольких многолучевых компонентов, поступивших по различным путям (с достаточно различающимися задержками). Таким образом, можно сказать, что при использовании RAKE-приемника в системе DS/SS получается разнесение по пути распространения. RAKE-приемник нужен при приеме, когерентном по фазе; но при дифференциально-когерентном обнаружении битов можно реализовать простую задержку (равную комплексно сопряженной длительности одного бита) [44].

• Расширение спектра методом скачкообразной перестройка частоты, (frequency-hopping spread-spectrum— FH/SS) также иногда используется в качестве механизма разнесения. В системе GSM применяется медленная перестройка частоты (217 скачков/с) для компенсации в трех случаях, когда объект движется очень медленно (или совсем не движется) и испытывает сильное замирание вследствие спектральных нулей.

• Пространственное разнесение (spatial divereity) обычно осуществляет-ся посредством множественных принимающих антенн, разнесенных на расстояние, не меньшее 10 длин волн при размещении на базовой станции (и меньше, при размещении на мобильном объекте). Для выбора наилучшего выхода антенн или для когерентного объединения всех выходов следует реализовать специальные методы обработки сигналов. В настоящее время также реализованы системы с множественными передатчиками, размещенными в разных местах, например система GPS (Global Positioning System — глобальная система навигации и определения положения).

• Поляризационное разнесение (polarization diversity) [45] — это еще один из способов получения дополнительных некоррелированных наборов сигнала.

• Любую схему разнесения можно рассматривать как тривиальную форму кода с повторениями (repetition code) в пространстве и во времени. В то же время существуют методы улучшения отношения SNR в каналах с замиранием, которые эффективнее и мощнее кодов с повторениями. Уникальный метод борьбы с ухудшением — это кодирование с коррекцией ошибок, поскольку он не обеспечивает большую энергию сигнала, а снижает требуемое , необходимое для достижения желаемой вероятности ошибки. Применение кодирования с коррекцией ошибок совместно с чередованием [19, 46-51] — это, пожалуй, наиболее распространенная схема улучшения рабочих характеристик системы в среде с замиранием. Следует отметить, что механизм рассеивания ошибок во время замирания посредством разнесения во времени зависит от движения переносного устройства. Чем больше скорость мобильного устройства, тем эффективнее эта схема; при низких скоростях эффективность мала. (Зависимость скорости передвижного устройства от характеристик устройства чередования продемонстрирована в разделе 15.5.6.)

15.5.4. Методы разнесения

Задачей реализации методов разнесения является использование дополнительных независимых (или, по крайней мере, некоррелирующих) путей прохождения сигнала для улучшения получаемого SNR. Разнесение может улучшить рабочие характеристики системы при сравнительно небольших затратах; в отличие от выравнивания, разнесение не требует служебных расходов на настройку. В этом разделе будет показано улучшение достоверности передачи, которое можно получить с помощью методов разнесения. Вероятность битовой ошибки , усредненная по всем «подъемам и спадам» канала с медленным замиранием, можно вычислить следующим образом.

(15.38)

Здесь РВ(х) вероятность битовой ошибки для данной схемы модуляции при заданном значении SNR = х, где х = а р(х) — плотность вероятности х при замирании. При постоянных Еb и N0, используется для обозначения изменений амплитуды вследствие замирания (см. раздел 15.2.2).

При релеевском замирании имеет релеевское распределение, так что² и х имеют ² - распределение. Таким образом, согласно уравнению (15.15),

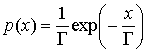
, (15.39)

где — это SNR, усредненное по всем подъемам и спадам замирания. Если каждая разнесенная ветвь (сигнала) имеет мгновенное значение SNR = и предполагается что каждая ветвь имеет одинаковое среднее значение SNR, равное Г, то получаем следующее.

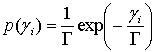
(15.40)

Вероятность того, что отдельная ветвь имеет SNR, меньшее порогового значения , равна следующему.

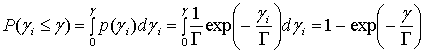(15.41)

Вероятность того, что все М независимых разнесенных ветвей сигнала получены одновременно с SNR, меньшим некоторого порогового значения , равна следующему.

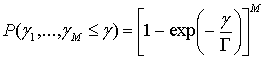(15.42)

Вероятность того, что любая ветвь сигнала имеет значения SNR>, равна следующему.

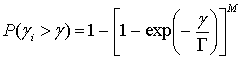(15.43)

Выражение (15.43) — это вероятность превышения порогового значения при разнесении с автовыбором.

Пример 15.1. Преимущество разнесения

Пусть используется разнесение на 4 ветви, и каждая ветвь получает независимый сигнал с релеевским замиранием. Среднее SNR равно Г = 20 дБ. Определите вероятность одновременного приема всех 4 ветвей с SNR, меньшим 10 дБ (а также вероятность того, что этот порог будет превышен). Сравните результаты с использованием разнесения и без него.

Решение

Используя уравнение (15.42) при =10дБ и /Г= 10дБ - 20дБ = 10дБ = =0,1, найдем вероятность того, что SNR упадет ниже 10 дБ.

При использовании разнесения получаем следующее.

Без разнесения

15.5.4.1. Комбинированные методы разнесения

Наиболее распространенные методы объединения разнесённых сигналов - это разнесение с автовыбором (selection diversity), разнесение с обратной связью (feedback diversity), разнесение с максимальным отношением (maximal ratio diversity) и разнесение с равным усилением (equal gain diversity). В системах, использующих пространственное разнесение, выбор включает дискретизацию М сигналов антенн и передачу на демодулятор наибольшего из них. При разнесении с автовыбором объединение сигналов реализуется относительно просто, однако оно не является оптимальным, поскольку в нем не используются одновременно все полученные сигналы.

При разнесении с обратной связью или при сканирующем разнесении (scanning diversity) не используется самый мощный из М сигналов; вместо этого М сигналов сканируются в определенной последовательности до тех пор, пока не будет найден сигнал, превышающий данное пороговое значение. Именно этот сигнал используется до тех пор, пока его уровень не опустится ниже установленного порогового значения, после чего процесс сканирования начинается снова. Достоверность этого метода несколько ниже, чем других методов, однако разнесение с обратной связью довольно просто реализовать.

При объединении разнесенных сигналов по принципу максимального отношения сигналы со всех М ветвей взвешиваются согласно их личным отношениям SNR, а затем суммируются. Перед суммированием требуется достичь синфазности суммируемых сигналов. Алгоритмы определения требуемого опережения или задержки сигнала аналогичны используемым в эквалайзерах и RAKE-приемниках. Суммирование с максимальным отношением дает среднее SNR , равное сумме отдельных средних SNR, как показано ниже.

(15.44)

Здесь предполагалось, что каждая ветвь имеет среднее SNR, равное = Г. Таким образом, объединение сигналов с максимальным отношением может дать приемлемое среднее SNR, даже если ни одно из средних значений не является приемлемым. В этом методе М ветвей суммируются синфазно, т.е. они умножаются на соответствующий весовой коэффициент так, чтобы на приемник подавался сигнал с наибольшим возможным SNR.

Объединение с равным усилением аналогично объединению с максимальным отношением, за исключением того, что все весовые коэффициенты равны единице. По-прежнему остается возможность достичь приемлемого значения SNR на выходе при большом числе неприемлемых значений на входе. Достоверность передачи при этом незначительно уступает достоверности при объединении с максимальным отношением (см. [52] для более детального ознакомления с объединением разнесенных сигналов).

15.5.5. Типы модуляции для каналов с замираниями

Очевидно, что схема передачи сигнала, основанная на преобразованиях амплитуды, такая как амплитудная манипуляция (amplitude shift keying — ASK) или квадратурная амплитудная модуляция (quadrature amplitude modulation — QAM), по сути, подвержена ухудшению качества передачи в среде с замиранием. Таким образом, для каналов с замираниями предпочтительно выбирать схемы передачи сигнала с частотным или фазовым типом модуляции.

При рассмотрении ортогональных схем модуляции FSK для каналов с замираниями удобно использовать схему MFSK (с M=8 или больше), поскольку ее достоверность выше, чем у схемы с передачей двоичного сигнала. В каналах с медленным релеевским замиранием двоичная DPSK и 8-FSK отличаются не более чем на 0,1 дБ друг от друга [19]. На первый взгляд, может показаться, что при повышении порядка ортогонального алфавита расширяется полоса пропускания, которая в какой-то момент превысит полосу когерентности, что приведет к частотно-селективному замиранию. Однако для схемы MFSK требуется доступная полоса передачи, намного превышающая ширину полосы распространяющегося сигнала. Например, рассмотрим схему 8-FSK и скорость передачи 10000 символов/с. Ширина полосы пропускания равна MRs=80000 Гц. Это ширина полосы частот, которая должна быть доступна для использования системой. Однако каждый раз при передаче символа отправляется не весь алфавит, а только один однополосный тон (занимающий в спектре 10000 Гц). При рассмотрении модуляции PSK для каналов с замираниями алфавиты модуляции более высокого порядка показывают плохую производительность, поэтому схем MPSK с M=8 или выше следует избегать [19]. Ниже в качестве некоторого обоснования такой точки зрения приводится пример 15.2, в котором рассмотрена система мобильной связи.

Пример 15.2. Изменения в системе мобильной связи

Доплеровское расширение fd = V/показывает, что скорость замирания непосредственно зависит от скорости движения. В табл. 15.2 показано доплеровское расширение в зависимости от скорости движения передвижного устройства для несущих частот 900 МГц и 1800 МГц. Вычислите изменение фазы, приходящееся на один символ, для передачи сигнала с модуляцией QPSK при скорости 24,310³ символов/с. Предполагается, что несущая частота равна 1800 МГц, а скорость передвижного устройства равна 50 миль/ч (80 км/ч). Повторите вычисления для скорости передвижного устройства, равной 100 миль/ч.

Решение

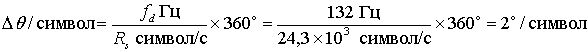
При скорости 100 миль/ч:

Таким образом, должно быть очевидно, почему MPSK со значением М>4 обычно не используется для передачи информации в среде с многолучевым распространением.

Таблица 15.2. Доплеровское расширение в зависимости от скорости мобильного устройства

Скорость		Доплеровское расширение (Гц)	Доплеровское расширение (Гц)
миль/ч	км/ч	900 МГц (=33 см)	1800 МГц (=16,6 см)
3 20 50 80 120	5 32 60 108 192	4 27 66 106 160	8 54 132 212 320

15.5.6. Роль чередования

Для передачи в среде с многолучевым распространением основным преимуществом чередования является осуществление временного разнесения (при использовании совместно с кодированием с коррекцией ошибок). Чем больше интервал времени, в течение которого канальные символы разделены, тем больше шансов, что смежные биты (после восстановления исходного порядка) будут подвержены нескоррелированным проявлениям замирания, таким образом, больше шансов достичь эффективного разнесения. На рис. 15.19 показаны преимущества введения интервала времени чередования Тп, большего времени когерентности канала Т0. Система имеет следующие параметры: модуляция DBPSK, декодирование согласно мягкой схеме принятия решений, сверточный код со степенью кодирования 1/2, К=7, канал испытывает медленное релеевское замирание. Должно быть очевидно, что устройство чередования, имеющее наибольшее отношение Тп/Т0, будет работать лучше всего (высокая частота появления ошибок при демодуляции ведет к низкой частоте появления ошибок декодирования). Это позволяет заключить, что Тп/Т0 должно быть каким-нибудь большим числом, скажем 1000 или 10000. В то же время в системах связи реального времени это невозможно, поскольку характерная временная задержка, связанная с чередованием, была бы чрезмерной. Как описывалось в разделе 8.2.1 для блочного чередования, перед передачей первой строки и первого столбца в память должен быть загружен практически весь массив. Подобным образом в приемнике перед операцией восстановления массива почти весь он должен быть сохранен. Это приведет к задержке, равной длительности одного блока данных, как в передатчике, так и приемнике. В примере 15.2 показано, что для сотовой системы телефонной связи с несущей частотой 900 МГц отношение Тп/Т0, равное 10, приблизительно составляет предел, при котором еще не наблюдается чрезмерной задержки.

Интересно отметить, что чередование не дает никаких преимуществ в отношении многолучевого распространения при отсутствии относительного движения передатчика и приемника (или движения объектов на путях распространения сигналов). Преимущества (касающиеся достоверности передачи в системе) обнаруживаются при увеличении скорости движения. (Не нужно использовать это в качестве оправдания превышения скорости на шоссе.)

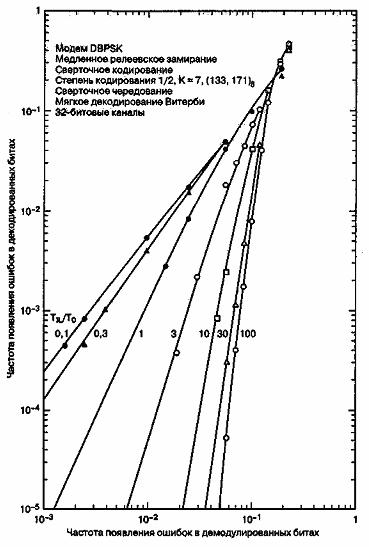
Рис. 15.19. Вероятность ошибки для различных отношений времени чередования к времени когерентности

На рис. 15.20, а показаны области, характеризуемые разными функциями замирания {}. В области между точками d0 и d1 функция замирания равна , между точками d1 и d2 - и т.д. Пусть точки di расположены через равное расстояние . На рис. 15.20, б показан автомобиль, движущийся с небольшой скоростью; когда он перемещается на расстояние , его передатчик успевает излучить девять символов. Допустим, что рабочий интервал устройства чередования - это три символа, так что символы s1–s2 появляются в произвольном порядке, показанном на рис. 15.20, б. Отметим, что все девять символов испытывают одинаковое замирание , так что после восстановления исходного сигнала мы не обнаружим никакого преимущества чередования. Рассмотрим теперь рис. 15.20, в, на котором автомобиль движется в 3 раза быстрее, чем на рис. 15.20, б; таким образом, когда он переместится на расстояние , его передатчик излучит только три символа. Как и ранее, символы подвержены замиранию, характерному для этой области. В результате этого получаем последовательность из девяти символов, показанную на рис. 15.20, в. После восстановления исходной последовательности из последовательности, показанной на рис. 15.20, в, получаем следующие пары «множитель замирания/символ»: , , , , , , . Можно видеть, что смежные символы искажаются вследствие влияния различных множителей замирания. Таким образом, чередование с временным периодом, слишком малым, чтобы давать хотя бы какие-нибудь преимущества при низких скоростях, оправдывает себя при более высоких скоростях.

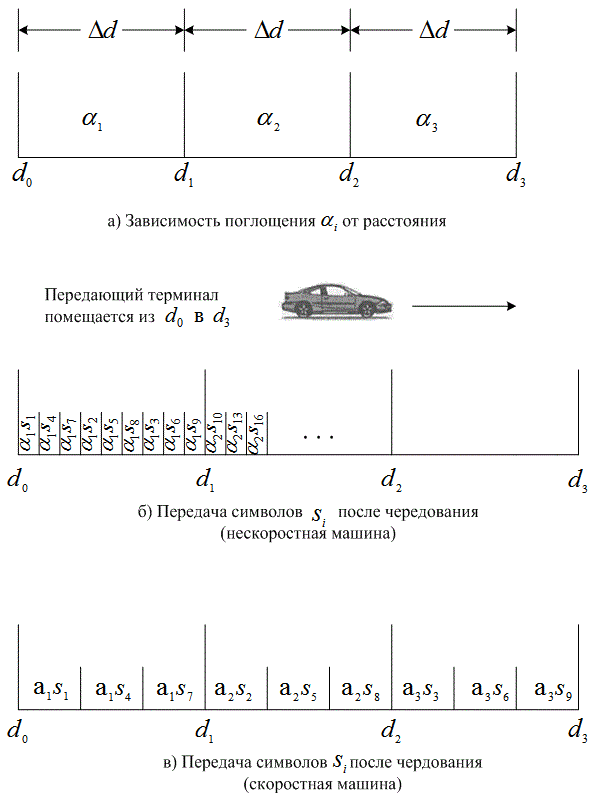
Рис. 15.20. Преимущества чередования при увеличении скорости радиостанции

На рис. 15.21 также показано, что хотя с увеличением скорости мобильного устройства качество связи и ухудшается (увеличивается скорость замирания), польза от чередования при этом возрастает. На рис. 15.21 представлены результаты эксплуатационных испытаний, проведенных на системе CDMA, удовлетворяющей стандарту Interim Specification 95 (IS-95), в канале, состоящем из движущегося устройства и базовой станции [53]. На рисунке показана зависимость отношения требуемого для поддержания частоты ошибок в кадрах (20 мс данных), равной 1%, от скорости передвижного устройства. Наилучшие характеристики (наименьшее требуемое ) достигаются при низких скоростях от 0 до 20 км/ч. Это область низких скоростей, в которой методы регулирования мощности в системе могут наиболее эффективно компенсировать эффекты медленного замирания; при низких скоростях чередование не приносит какой-либо пользы, и на графике показано сильное ухудшение характеристик как функция скорости. При скорости порядка 20-60 км/ч крутизна этого ухудшения уменьшается. Это область, в которой регулирование мощности в системе уже не позволяет полностью справиться с возрастанием скорости замирания, и в то же время использование чередования еще не приносит достаточной пользы. На скорости 60 км/ч достоверность передачи для такой системы достигает наихудшего значения. Когда устройство движется более 60 км/ч, контроль мощности уже не позволяет как либо бороться с замиранием, однако чередование обеспечивает неизменное улучшение характеристик при увеличении скорости. Задача устройства чередования, заключающаяся в преобразовании эффектов глубокого замирания (коррелирующие во времени события) в случайные события, упрощается с ростом скорости. Итак, достоверность передачи по каналу с замираниями обычно ухудшается с ростом скорости, поскольку возрастает доплеровское расширение или скорость замирания. В то ж время использование чередования, которое становится более эффективно при высоких скоростях, приводит к ослаблению эффектов ухудшения. Эта тенденция повышения достоверности передачи не может продолжаться бесконечно. В конечном счет производительность системы достигает уровня неустранимых ошибок, показанного на рис. 15.15. Следовательно, если бы измерения, показанные на рис. 15.21, проводились] при скоростях, превышающих 200 км/ч, то на графике была бы точка, в которой кривая развернулась бы круто вверх, что соответствовало бы ухудшению рабочих характеристик, вызванному возрастанием доплеровского эффекта.

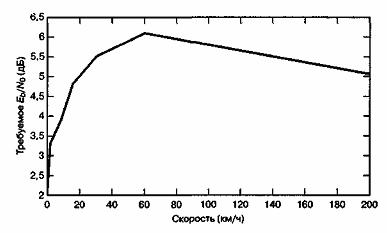
Рис. 15.21. Типичная зависимость требуемого от скорости движения. Используется релеевский канал с двумя независимыми путями распространения, частота передачи 850 МГц, частота появления ошибочных кадров 1%.

15.6. Краткий обзор ключевых параметров, характеризующих каналы с замираниями

Подытожим условия, которым должна удовлетворять система, чтобы канал не вносил частотно-селективного искажения и искажения, вызванного быстрым замиранием. Объединив выражения (15.22), (15.32) и (15.33), получаем следующее.

f0 >W >fd (15.45)

или

Tm<Ts<T0 (15.46)

Иными словами, желательно, чтобы полоса когерентности канала превышала скорость передачи сигналов, которая, в свою очередь, должна превышать скорость замирания в канале. Напомним, что если не бороться с искажениями, то f0 устанавливает верхний предел, a fd — нижний предел скорости передачи сигнала.

15.6.1. Искажения вследствие быстрого замирания: случай 1

Если условия (15.45) и (15.46) не выполняются, искажения будут происходить до тех пор, пока не будут приняты подходящие меры. Рассмотрим быстрое замирание, при котором скорость передачи сигналов меньше скорости замирания в канале.

f0 >W<fd (15.47)

Борьба с искажениями заключается в использовании одного или нескольких перечисленных ниже методов (см. рис. 15.18).

• Выбирается метод модуляции/демодуляции, наиболее устойчивый в условиях быстрого замирания. Это значит, например, что необходимо избегать схем, которые требуют контуров ФАПЧ для восстановления несущей, поскольку быстрое замирание может не позволить контурам ФАПЧ достичь синхронизации.

• Вводится достаточная избыточность, чтобы скорость передачи симво-лов превышала скорость замирания в канале, но в то же время не превышала ширины полосы когерентности. Тогда канал можно классифицировать как проявляющий амплитудное замирание. Однако, как было показано в разделе 15.3.3, даже каналы с амплитудным замиранием будут испытывать частотно-селективное замирание всегда, когда передаточная функция проявляет спектральный нуль вблизи центра полосы сигнала. Поскольку это происходит только иногда, бороться с искажением можно путем выбора адекватного кода коррекции ошибок и использования чередования.

• Описанные выше два способа борьбы с искажением могут привести к тому, что демодулятор будет работать возле релеевского предела [19] (см. рис. 15.17). В то же время график зависимости вероятности ошибки от может спрямляться (как это показано на рис. 15.15) вследствие частотно-модулированного шума, который является результатом случайного доплеровского расширения. Использование внутриполосного контрольного тона и контура стабилизации частоты может снизить уровень, при котором характеристика спрямляется.

• Чтобы избежать эффекта дна ошибки вследствие случайного допле-ровского расширения, скорость передачи сигналов должна увеличиться до величины, превышающей скорость замирания приблизительно в 100-200 раз [27]. Это один из мотивов разработки мобильных систем связи, работающих в режиме множественного доступа с временным разделением (time-division multiple access — TDMA).

• Применяется кодирование с коррекцией ошибок и чередование для до-полнительного улучшения рабочих характеристик системы.

15.6.2. Искажения вследствие частотно-селективного замирания: случай 2

Рассмотрим частотно-селективное замирание, при котором ширина полосы когерентности меньше скорости передачи символов, в то время как скорость передачи символов больше доплеровского расширения.

f0 <W >fd (15.48)

Поскольку скорость передачи символов превышает скорость замирания в канале, искажения вследствие быстрого замирания отсутствуют. В то же время необходимо ослабить частотно-селективные эффекты. Борьба с искажениями заключается в использовании одного или нескольких перечисленных ниже методов (см. рис. 15.18).

• Адаптивное выравнивание, расширение спектра (методом прямой последовательности или скачкообразной перестройки частоты), OFDM, контрольный сигнал. В европейской системе GSM в каждый временной интервал передачи выводится некоторая контрольная последовательность, помогающая приемнику определить импульсную характеристику канала. Для ослабления частотно-селективных искажений применяется эквалайзер Витерби (рассматривается ниже).

• Когда воздействие искажений ослаблено, для приближения к харак-теристикам канала AWGN можно использовать методы частотного разнесения (а также кодирование с коррекцией ошибок и чередование). Для передачи спектра, расширенного методом прямой последовательности (direct-sequence spread-spectrum — DS/SS), разнесение может реализоваться посредством использования RAKE-приемника (рассматривается ниже), выполняющего когерентное объединение многолучевых компонентов, которые в противном случае были бы утеряны.

15.6.3. Искажения вследствие быстрого и частотно-селективного замирания: случай 3

Пусть ширина полосы когерентности канала меньше скорости передачи сигналов, которая, в свою очередь, меньше скорости замирания. Это условие математически выражается следующим образом.

f0 <W <fd (15.49)

или

f0 <fd (15.50)

Очевидно, что канал проявляет как быстрое, так и частотно-селективное замирание. Напомним из уравнений (15.45) и (15.46), что f0 устанавливает верхний предел, a fd — нижний предел скорости передачи сигналов. Таким образом, условие (15.50) представляет собой сложную проектную задачу, поскольку, если не обеспечено подавление искажений, максимально допустимая скорость передачи сигнала будет, собственно говоря, меньше минимально допустимой скорости передачи сигналов. Борьба с искажением в этом случае выполняется подобно тому, как это рекомендовалось в случае 1.

• Выбирается метод модуляции/демодуляции, наиболее устойчивый в условиях быстрого замирания.

• Для увеличения скорости передачи символов используется избыточ-ность передачи.

• Вводятся какие-либо типы подавления искажений, вызванных частотно-селективным замиранием, подобно описанным в случае 2.

• Когда воздействие искажений было подавлено, вводится какой-либо тип разнесения (а также кодирование с коррекцией ошибок и чередование) с целью приближения к характеристикам канала AWGN.

Пример 15.3. Эквалайзеры и устройства чередования в мобильной связи

Рассмотрим сотовый телефон, который размещен на объекте, движущемся со скоростью 60 миль в час (96 км/ч). Несущая частота равна 900 МГц. С помощью тестового профиля эквалайзера GSM, показанного на рис. 15.22, определите следующее: а) среднеквадратический разброс задержек ; б) максимально допустимую ширину полосы сигнала , при которой не требуется эквалайзер; в) считая, что разброс задержек в канале равен найденному в п. а, какая из следующих систем требует использования эквалайзера: цифровой сотовый стандарт США (United States Digital Cellular Standard — USDC), известный как IS-54 (новая версия — IS-136), глобальная система мобильной связи (Global System for Mobile — GSM), системы CDMA, разработанные согласно IS-95; ширина полос и скорость передачи символов для этих систем равны следующему: USDC - W =30 кГц, 1/Ts= 24,310³ символа/с; GSM - W= 200 кГц, 1/Ts = 27110³ символа/с; IS-95 - W= 1,25 МГц, 1/Ts = =9,610³ символа/с; г) общую (передатчик плюс приемник) задержку, вносимую устройством чередования, когда отношение рабочего интервала устройства к времени когерентности Tп/T0 равно 10 (если общая приемлемая задержка (передатчик плюс приемник) для речи равна 100 мс, можно ли использовать устройство с описанными выше характеристиками для передачи речи?); д) повторите пп. а-г для несущей частоты 1900 МГц.

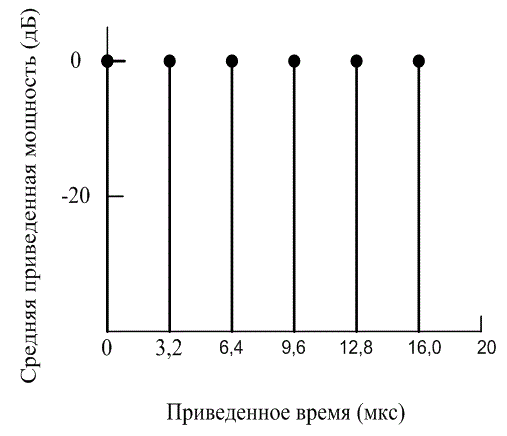
Рис. 15.22. Тестовый профиль эквалайзера GSM

Решение

а) На рис. 15.22 тестовый профиль системы GSM показывает идеализированный компонент многолучевого распространения, расположенный через каждые шесть интервалов задержки {} в промежутке от 0 до 16 мкс. Каждый компонент можно обозначить через S(), его среднюю относительную мощность, которая на этом профиле одинакова для всех компонентов (0 дБ). Профиль представляет мнимую многолучевую среду, используемую при тестировании перед выравниванием [15]. При таком расположении компонентов, как показано на рисунке, средний разброс задержек будет иметь следующий вид.

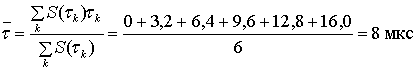
fd = = 169 Гц, следовательно, Т0= = Змс

Таким образом, рабочий интервал устройства чередования равен Тп = 30 мс; это даст общую задержку передатчика и приемника, равную 60 мс, что является приемлемым значением для речевого сигнала.

15.7. Приложения: борьба с эффектами частотно-селективного замирания

15.7.1. Применение эквалайзера Витерби в системе GSM

На рис. 15.23 показан кадр (длительность 4,615 мс) схемы множественного доступа с временным разделением (time-division multiple access — TDMA) в системе GSM, состоящий из 8 слотов, каждый из которых присвоен активному мобильному клиенту. Обычный пакет передачи, занимающий один интервал, состоит из 57 бит сообщения, расположенных по обе стороны от 26-битовой последовательности, иногда называемой зондирующей (sounding) или настроечной (training). Длительность одного слота составляет 0,577 мс (или скорость передачи равна 1733 слота/с). Задача внутренней контрольной последовательности — помочь приемнику в адаптивном определении импульсной характеристики канала (за время передачи одного слота, т.е. 0,577 мс), Чтобы данный метод был эффективным, характеристики замирания в канале должны оставаться неизменными в течение времени, приблизительно равного длительности одного слота. Иначе говоря, за время передачи одного слота, пока приемник анализирует искажение контрольного блока, не должно проявиться быстрое замирание; в противном случае компенсация замирания в канале окажется неэффективной. В качестве примера можно взять приемник GSM, находящийся на скоростном поезде, который движется с постоянной скоростью 200 км/ч (около 55,56 м/с). Частота несущей 900 МГц (длина волны = 0,33 м). Из уравнения (15.29) время, соответствующее проходу половины длины волны, равно следующему.

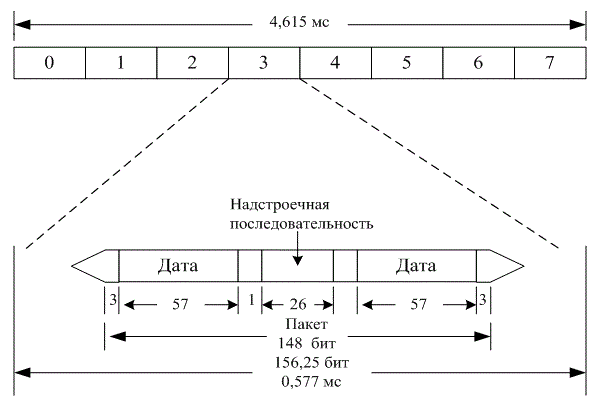
Рис. 15.23. Кадр TDMA GSM и временной слот, содержащий

нормальный пакет

Второй момент разброса задержек и среднеквадратический разброс задержек имеют следующий вид:

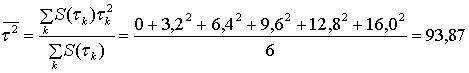мкс²

и, с помощью уравнения (15.17),

= 5,5 мкс

б) С помощью уравнения (15.21) полоса когерентности канала будет определена следующим образом.

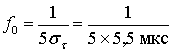= 36,4 кГц

Таким образом, максимально допустимая полоса пропускания сигнала, при которой не нужно использовать эквалайзер, будет W=36,4 кГц.

в) Для полос пропускания различных систем, данных в этом примере, очевидно, что использование эквалайзера в USCD не обязательно, тогда как в GSM он действительно нужен. Относительно систем, которые разрабатывались согласно IS-95, можно сказать следующее: поскольку скорость передачи сигналов или полоса пропускания W, равная 1,25 МГц, значительно превышает полосу когерентности 36,4 кГц, система проявляет частотно-селективное замирание. В то же время в таких системах с расширением спектра методом прямой последовательности (direct-sequence spread spectrum - DS/SS), W умышленно расширяется с целью превышения f0, и, следовательно, подавления эффектов частотно-селективного замирания. Необходимость в эквалайзере возникает только тогда, когда проблему представляет межсимвольная интерференция (intersymbol interference — ISI), но ISI не является проблемой, если скорость передачи символов меньше полосы когерентности (или длительность символа больше многолучевого разброса). Следовательно, в случае IS-95 эквалайзер не нужен, поскольку скорость передачи 9,610³ символов/с значительно ниже полосы когерентности. Для разнесения путей применяется описываемый в разделе 15.7.2 RAKE - приемник; на уровне элементарных сигналов его реализация сходна с реализацией эквалайзера.

г) Чтобы определить задержку, вносимую устройством чередования, рассчитаем доплеровское расширение и время когерентности с помощью уравнений (15.25) и (15.29).

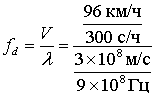=80 Гц, следовательно, мс

Исходя из того, что Tп/T0 = 10, рабочий интервал устройства чередования равен Тп = 63 мс. Из этого следует, что общая задержка передатчика и приемника равна 126 мс. Для передачи речи это значение несколько превышает приемлемое. В мобильных системах часто применяются устройства с более короткими рабочими интервалами, которые дают односторонние задержки порядка 20-40 мс.

д) Повторяем расчеты для несущей частоты 1900 МГц. На вычисление полосы когерентности смена несущей не оказывает никакого влияния, а вот доплеровское расширение, время когерентности и задержку чередования нужно рассчитывать заново. Итак,

(15.51)

Как показывает уравнение (15.51), это приблизительно отвечает времени когерентности. Следовательно, время когерентности канала более чем в 5 раз превышает время передачи одного слота (0,577 мс). Время, необходимое для значительного изменения характеристик замирания в канале, относительно велико по сравнению со временем передачи одного слота. Отметим, что выбор, сделанный в системе GSM при подборе времени передачи слота TDMA и контрольного блока, несомненно, был осуществлен при учете необходимости устранения эффектов быстрого замирания, которые могут свести на нет эффективность работы эквалайзера. Скорость передачи символов в стандарте GSM (или скорость передачи битов, если используется двоичная модуляция) равна 271 000 символов/с, а полоса пропускания W составляет 200 кГц. Поскольку среднеквадратический разброс задержек о, в городской местности равен порядка 2 мкс, то, исходя из уравнения (15.21), можно видеть, что результирующая полоса когерентности f0 будет приблизительно равна 100 кГц. Следовательно, очевидно, что поскольку f0 < W, приемник GSM должен иметь средства для борьбы с частотно-селективным искажением. Как правило, для этого используется эквалайзер Витерби.

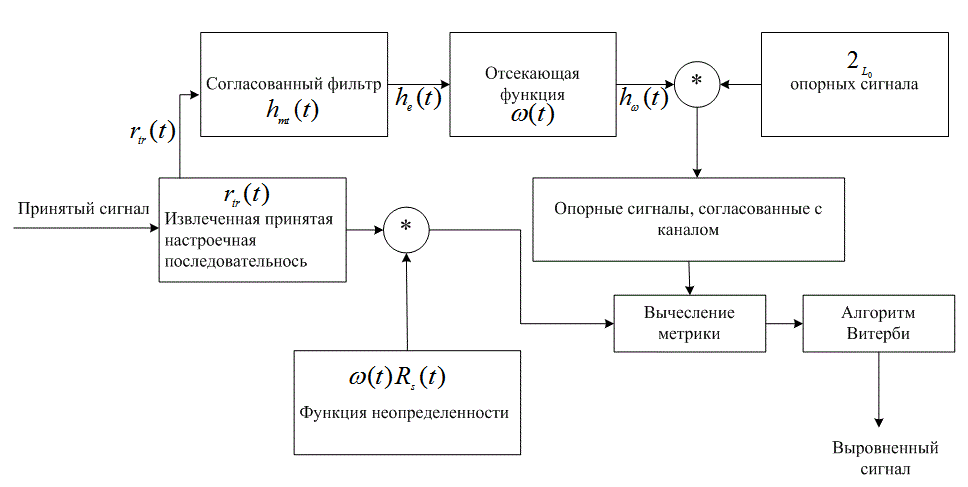
Рис. 15.24. Применение эквалайзера Витерби в системе GSM

На рис. 15.24 изображена блок-схема приемника GSM для оценки импульсной характеристики канала. Эта оценка нужна детектору для получения опорных сигналов, согласованных с состоянием канала [54], что будет объяснено ниже. Наконец, для оценки битов сообщения с максимальным правдоподобием используется алгоритм Витерби. Принятый сигнал можно описать через переданный сигнал, свернутый с импульсной характеристикой канала. Обозначим через str(t) переданную контрольную последовательность, а через rtr(t) — соответствующую принятую последовательность.

rtr(t)= str(t)*hc(t) (15.52)

В данном случае "*" означает операцию свертки, причем шумом мы пренебрегаем. В приемнике, поскольку rtr(r) является частью принятого нормального пакета, она извлекается и отсылается на фильтр с импульсной характеристикой hmf(t), который согласован с str(t). Этот согласованный фильтр выдает оценку hc(t), обозначаемую как he(t), которая, согласно (15.25), записывается следующим образом.

he(t)= rtr(r)* hmf(t)= str(t)* hc(t)* hmf(t)=Rs(t)hc(t) (15.53)

Здесь Rs(t)= str(t)* hmf(t) - автокорреляционная функция str(t). Если str(t) предназначена для получения очень короткой (импульсного типа) автокорреляционной функции Rs(t), тогда he(t)= hc(t). Далее, при использовании отсекающей функции w(t), he(t) усекается до функции hw(t), которую уже можно обрабатывать численно. Временная длительность w(t), обозначаемая как L0, должна быть достаточно большой для компенсации эффектов типичной ISI, введенной каналом. Член L0 образуется в результате двух вкладов, а именно: LCISI соответствующий управляемой ISI, вызванной гауссовой фильтрацией полосового сигнала (который затем модулирует несущую согласно схеме MSK), и Lc, соответствующий вводимой каналом ISI, которая вызвана многолучевым распространением. Таким образом, L0 можно записать следующим образом.

L0 = LCISI + Lc

В системе GSM требуется обеспечить подавление искажений, вызванных дисперсией сигнала, имеющего разброс задержек порядка 15-20 мкс. Поскольку в GSM длительность бита составляет 3,69 мкс, L0 можно выразить в единицах битовых интервалов. Следовательно, эквалайзер Витерби, применяемый в системе GSM, обладает памятью от 4 до 6 битовых интервалов. На каждом интервале L0 бит задача эквалайзера Витерби состоит в нахождении наиболее правдоподобной последовательности, длиной L0 бит, среди возможных, которые могли быть переданы. Определение наиболее правдоподобной L0 - битовой последовательности, которая могла быть передана, требует создания значащих опорных сигналов путем модификации (или искажения) идеальных сигналов (генерируемых приемником) таким образом, как канал искажает передаваемый слот. Следовательно, опорных сигналов сворачиваются с усеченной оценкой импульсной характеристики канала hw(t) с целью генерации искаженных или своего рода подогнанных под канал опорных сигналов. Затем подкорректированные сигналы сравниваются с принятыми информационными сигналами для расчета метрик. Отметим, что перед сравниванием принятые данные сворачиваются с известной усеченной автокорреляционной функцией w(t)Rs(t), преобразовывая ее подобно опорным сигналам. Такой фильтрованный сигнал сообщения сравнивается с возможными подкорректированными опорными сигналами, причем способ получения метрик подобен способу, использованному в алгоритме декодирования Витерби (Viterbi decoding algorithm — VDA). Алгоритм VDA дает максимально правдоподобную оценку переданной последовательности данных [34].

Отметим, что в большинстве методов выравнивания для компенсации неоптимальных свойств hc(t) применяются фильтры, т.е. выравнивающие фильтры пытаются модифицировать искаженные формы импульсов. В то же время эквалайзер Витерби работает иным образом. Он включает измерение hc(t), а затем предоставляет способ подгонки приемника под среду канала. Целью такой подгонки является попытка помочь детектору в оценке искаженной последовательности импульсов. При наличии эквалайзера Витерби искаженные выборки не меняют формы и не компенсируются прямо каким-либо иным методом; приемник не подавляет сигнал, он перестраивается таким образом, что становится способен к более эффективной обработке искаженных фрагментов.

15.7.2. RAKE-приемник в системах с расширением спектра методом прямой последовательности

Стандарт IS-95 определяет систему сотовой связи DS/SS, в которой для разнесения путей распространения используется RAKE-приемник (RAKE receiver) [35—37]. Данный приемник изучает различные многолучевые задержки на предмет кодовой корреляции, потом соответствующим образом восстанавливает задержанные сигналы, которые затем оптимально сочетаются с выходом других независимых корреляторов. На рис. 15.25 показаны профили мощности сигнала, соответствующие пяти передачам элементарных сигналов кодовой последовательности 1 0 1 1 1, причем моменты наблюдения обозначены как t-4 — для самого раннего наблюдения и t0 — длясамого позднего. На осях абсцисс показаны три компонента, поступающих с задержками . Полагается, что интервалы между моментами передачи ti и интервалы между моментами задержек равны по длительности одному элементарному сигналу. Отсюда можно сделать вывод, что компонент, поступающий на приемник в момент t-4 сзадержкой , совпадает по времени с двумя другими компонентами, а именно: поступающими в моменты t-3 и t-2 с задержками и соответственно. Поскольку в этом примере задержанные компоненты разделены, по крайней мере, временем одного элементарного сигнала, то их можно разрешить. В приемнике должен быть блок зондирования, предназначенный для оценки времени задержки . Следует отметить, что для мобильных наземных систем радиосвязи скорость замирания относительно низка (порядка миллисекунд) или, иначе говоря, когерентность канала довольно высока по сравнению с длительностью элементарного сигнала (Т0 > Tch). Таким образом, изменения проявляются достаточно слабо, чтобы приемник успел подстроиться к ним.

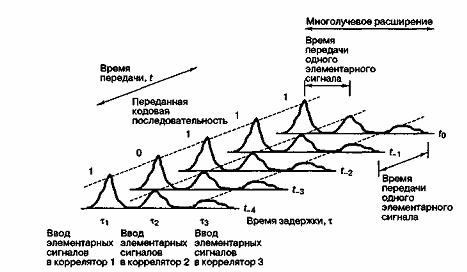
Рис. 15.25. Принимаемые элементарные сигналы в трехкомпонентном RAKE-приемнике

После оценки задержек для восстановления каждого разрешимого многолучевого компонента используется отдельный коррелятор. В данном примере подразумевается три таких коррелятора, каждый из которых будет обрабатывать запаздывающую версию одной и той же последовательности элементарных сигналов 1 0 1 11. На рис. 15.25 каждый коррелятор принимает элементарные сигналы с профилем мощности, представляющим собой последовательность компонентов, расположенную вдоль диагональной линии. Для простоты все элементарные сигналы показаны как положительные сигнальные посылки. В действительности эти элементарные сигналы образуют шумоподобную последовательность, которая, конечно, содержит и положительные, и отрицательные импульсы. Каждый из корреляторов пытается скоррелировать эти поступающие элементарные сигналы с таким же соответствующим образом синхронизированным псевдослучайным кодом. В конце символьного интервала (как правило, на один символ приходится сотни или даже тысячи элементарных сигналов) выходы корреляторов когерентно объединяются, после чего принимается решение относительно значения принятого символа. На рис. 15.26 показано фазовое вращение компонентов (Fi), выполняемое RAKE-приемником для облегчения когерентного объединения сигналов. На уровне элементарных сигналов RAKE-приемник подобен эквалайзеру, но его действительная функция заключается в разнесении путей распространения.

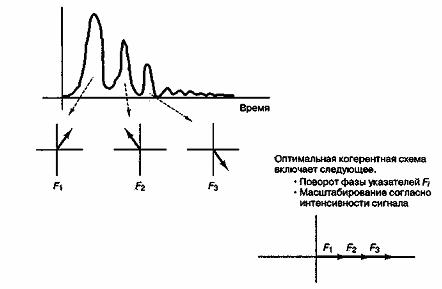
Рис. 15.26. Когерентное объединение многолучевых вкладов в RAKE-приемнике

Способность систем DS/SS к подавлению помех основывается на том, что кодовая последовательность, поступающая на приемник со сдвигом по времени лишь на один элементарный сигнал, будет иметь очень низкую корреляцию с конкретным псевдослучайным кодом, с которым коррелировала исходная последовательность. Следовательно, любые кодовые элементарные сигналы, запаздывающие на один или более элементарных интервалов, будут подавляться коррелятором. Задержанные элементарные сигналы всего лишь вносят вклад в возрастание уровня интерференции (корреляционных боковых лепестков). Подавление, которое осуществляет RAKE-приемник, можно назвать разнесением путей распространения, так как он осуществляет объединение энергии элементарных сигналов, которые поступают по многим путям распространения. Без RAKE-приемника эта энергия была бы потеряна для приемника DS/SS. Если на рис. 15.25 обратить внимание на картину над точкой , можно сделать вывод, что существует интерференция между элементарными сигналами вследствие одновременного поступления разных компонентов. Эффективность, получаемая в результате расширения спектра, позволяет системе выдерживать такую интерференцию на уровне элементарных сигналов. Считается, что другой коррекции в стандарте IS-95 не нужно.

Литература

1. Rappaport Т. S. Wireless Communications. Chapter 3 and 4, Prentice Hall, Upper Saddle River, New Jersey, 1996.

2. Greenwood D. and Hanzo L. Characterization of Mobile Radio Channels. Mobile Radio Communications, edited by R. Steele, Chapter 2, Pentech Press, London, 1994.

3. Lee W. C. Y. Elements of Cellular Mobile Radio Systems. IEEE Trans, on Vehicular Technology, vol. V-35, n. 2, May, 1986, pp. 48-56.

4. Okumura Y., et. al. Field Strength and its Variability in VHP and UHF land Mobil Radio Service. Review of the Elec. Comm. Lab., vol. 16, n. 9 & 10, 1968, pp. 825-873.

5. Hata M. Empirical Formulae for Propagation Loss in Land Mobile Radio Services. IEEE Trans, on Vehicular Technology, vol. VT-29, n. 3, 1980, pp. 317-325.

6. Seidel S. Y. et. al. Path Loss, Scattering and Multipath Delay Statistics in Four European Cities for Digital Cellular and Microcellular Radiotelephone. IEEE Transactions on Vehicular Technogy, vol. 40, n. 4, November, 1991, pp. 721-730.

7. Cox D. C., Murray R. and Norris, A. 800 MHz Attenuation Measured in and around Suburban Houses. AT&T Bell Laboratory Technical Journal, vol. 673, n. 6, July-August, 1984, pp. 921-954.

8. Schilling D. L., et. al. Broadband CDMA for Personal Communications Systems. IEEE Communications Magazine, vol. 29, n. 11, November 1991, pp. 86-93.

9. Andersen J. В., Rappaport T. S., Yoshida S. Propagation Measurements and Models for Wireless Communications Channels. IEEE Communications Magazine, vol. 33, n. 1, January, 1995, pp. 42-49.

10. Proakis J. G. Digital Communications, Chapter 7. McGraw-Hill Book Company, New York, 1983.

11. Schwartz M. Information, Transmission, Modulation, and Noise, Second Edition. McGraw-Hill, New York, 1970.

12. Amoroso F. Investigation of Signal Variance, Bit Error Rates and Pulse Dispersion for DSPN Signaling in a 'Mobil Dense Scatterer Ray Tracing Model. Int'l Journal of Satellite Communications, vol. 12, 1994, pp. 579-588.

13. Bello P. A. Characterization of Randomly Time-Variant Linear Channels. IEEE Trans, on Commun. Syst., December, 1963, pp. 360-393.

14. Green P. E. Jr. Radar Astronomy Measurement Techniques. MIT Licoln Laboratory, Lexington, Mass., Tech Report No. 282, December, 1962.

15. Pahlavan K. and Levesque A. H. Wireless Information Nerworks. Chapters 3 and 4. John Wiley and Sons, New York, 1995.

16. Lee W. Y. C. Mobil Cellular Communications. McGraw-Hill Book Co., New York, 1989.

17. Amoroso F. Use of DS/SS Signaling to Mitigate Rayleigh Fading in a Dens Scatterer Environment. IEEE Personal Communications, vol. 3, n. 2, April, 1996, pp. 52-61.

18. Clarke R. H. A Statistical Theory of Mobile radio Reception. Bell System Technical J., vol. 47, n. 6, July-August, 1968, pp. 957-1000.

19. Bogusch, R. L. Digital Communications in Fading Channels: Modulation and Coding. Mission Research Corp., Santa Barbara, California, Report no. MRC-R-1043, March, 11, 1987.

20. Amoroso F. The Bandwidth of Digital Data Signals. IEEE Communications Magazine, vol. 18, n. 6, November, 1980, pp. 13-24.

21. Bogusch R. L. et. al. frequency Selective Propagation Effects on Spread-Spectrum Receiver Tracking. Prceedings of the IEEE, vol. 69, n. 7, July, 1981, pp. 787-796.

22. Jakes W. C. (Ed.) Microwave Mobile Communications. John Wiley & Sons, New York, 1974.

23. Joint Tchnical Committee of Committee Tl R1P1.4 and TLA TR46.33/TR45.4.4 on Wireless Access. "Draft Final Report on RF Channel Characterization," Paper No. JTC(AIR)/94.01.17-238R4, January, 17, 1994.

24. Bello, P. A. and Nelin, B. D., "The Influence of Fading Spectrum on the Binary Error Probabilities of Incoherent and Differentially Coherent Matched Filter Receivers," IRE Transactions on Commun. Syst., vol. CS-10, June, 1962, pp. 160-68.

25. Amoroso F. Instantaneous Frequently Effects in a Doppler Scattering Environment. IEEE Enternational Conference on Communications, June, 7-10, 1987, pp. 1458-1466.

26. Fung V., Fappaport T. S. and Thoma B. Bit-Error Simulation for /4 DQPSK Mobile Radio Communication Using Two-Ray and Measurement-Base Impulse Response Models. IEEE J. Sel. Areas Commun., vol. 11, n. 3, April, 1993, pp. 393-394.

27. Bateman A. J. and McGeehan J. P. Data Transmission over UHF Fading Mobile Radio Channels. IEEE Proceedings, vol. 131, Pt. F, n. 4, July, 1984, pp. 364-374.

28. Feher K. Wireless Digital Communications, Prentice Hall, Upper Saddle River, New Jersey, 1995.

29. Davarian F., Simon M. and Sumida J. OMSK: A Practical 2400-bps Receiver for the Mobile Satellite Service. Jet Propulsion Laboratory Publication 85-51 (MSAT-X Report No. Ill), June, 15, 1985.

30. Rappaport T. S. Wireless Communicatios. Chapter 6. Prentice Hall, Upper Saddle River, New Jersey, 1996.

31. Bogousch R. L., Guigliano F. W. and Knepp D. L. Frequency-Selective Scintillation Effects and Decision Feedback Equalization in High Data-Rate Satellite Links. Proceedings of the IEEE, vol 71, n. 6, June, 1983, pp. 754-767.

32. Qureshi S. U. H. Adaptive Equalization. Proceedings of the IEEE, vol. 73, n. 9, September, 1985, pp. 1340-87.

33. Forney G. D. The Yiterbi Algprithm. Proceedings of the IEEE, vol. 61, n. 3, March, 1978, pp. 268-278.

34. Viterbi A. J. and Omura J. K. Principles of Digital Communication and Coding. McGraw-Hill, New York, 1979.

35. Price R. and Green P. E. Jr. A Communication Technique for Multipath Channels. Proceeding of the IRE, March, 1958, pp. 555-570.

36. Turin G. L. Introduction to Spread-Spectrum Amtimultipath Techniques and their Application to Urban Digital Radio. Proceedings of the IEEE, vol. 68, n. 3, March, 1980, pp. 328-353.

37. Simon M. K., Omura J. K., Scholtz R. A. and Levitt В. К. Spread Spectrum Communications Handbook. McGraw-Hill Book Co., 1994.

38. Birchler M. A. and Jasper S. С. А 64 kbps Digital Land Mobile Radio System Employing M-16QAM. Proceedings of the 1992 IEEE Int'l. Conference on Selected Topics in Wireless Communications, Vancouver, British Columbia, June, 25-26, 1992, pp. 158-162.

39. Sari H., Karam G. and Jeanclaude I. Transmission Techniques for Digital Terrestrial ТУ Broadcasting. IEEE Communications Magazine, vol. 33, n. 2, February, 1995, pp. 100-109.

40. Cavers J. K, The Performance of Phase Locked Transparent Tone-in-Band with Symmetric Phase Detection. IEEE Trans, on Commun., vol. 39, n. 9, September, 1991, pp. 1389-1399.

41. Moher M. L. and Lodge J. H. TCMP—A Modulation and Coding Strategy for Rician Fading Channel. IEEE Journal on Selected Areas in Communications, vol. 7, n. 9, December, .1989, pp. 1347-1355.

42. Harris F. On the Relationship Between Multirate Polyphase FIR, Filters and Windowed, .Overlapped FFT Processing. Proceedings of the Tweinty Third Annual Asilomar Conference on Signals, Systems, and Computers, Pacific Grove, California, October, 30 to November, 1, 1989, pp. 485-488.

43. Lowdermilk R. W. and Harris F. Design and Performance of Fading'Insensitive Orthogonal Frequency Division Multiplexing (OFDM) using Polyphase Filtering Techniques. Proceedings of the Thirtieth Annual Asilomar Comference on Signals, Systems, and Computers, Pacific Grove, California, November, 3-6, 1996.

44. Kavehrad M. and Bodeep G. E. Design and Experimental Results for a Direct Sequence Spread-Spectrum Radio Using Differential Phase-Shift Keying Modulation for Indoor Wireless Communications. IEEE JSAC, vol. SAC-5, n. 5, June, 1987, pp. 815-23.

45. Hess G. C. Land-Mobil Radio System Engineering. Artech House, Boston, 1993.

46. Hagenauer J. and Lutz E. Forward Error Correction Coding for Fading Compensation in Mobile Satellite Channels. IEEE JSAC, vol. SAC-5, n. 2, February, 1987, pp. 215-225.

47. McLane P. I., et al. PSK and DPSK Trellis Codes for Fast Fading, Shadowed Mobile Satellite Communication Channels. IEEE Trans, on Comm., vol. 36, n. 11, November, 1988, pp. 1242-1246.

48. Schlegel C. and Costello D. J. Jr. Bandwidth Efficient Coding for Fading Channels: Code Construction and Performance Analysis. IEEE JSAC, vol. 7, n. 9, December, 1989, pp. 1356-1368.

49. Edbauer F. Performance of Interleaved Trellis-Coded Differential 8-PSK Modulation over Fading Channals. IEEE J. on Selected Areas in Comm., vol. 7, n.9, December, 1989, pp. 1340-1346.

50. Solimari S. and Mokrani K. Performance of Coded Systems over Fading Dispersive Channels. IEEE Trans, on Communications, vol. 40, n. 1, January, 1992, pp. 51-59.

51. DivsalarD. and Pollara, F. Turbo Codes for PCS Applications. Proc. ICC'95, Seattle, Washington, June, 18-22, 1995, pp. 54-59.

52. Simon M. and Alouini M-S. Digital Communications over Fading Channels: A Unified Approach to Performance Analysis. John Wiley, New York, 2000.

53. Padovani R. Reverse Link Performance of IS-95 Based Cellular Systems. IEEE Personal Communications, Third Quarter 1994, pp. 28-34.

54. Hanzo L. and Stefanov J. The Pan-European Digital Cellular Mobile Radio System-Know as GSM. Mobile Radio Communications, edited by R. Steele, Chapter 8, Pentech Press, London, 1992.

Задачи

15.1. Функция плотности вероятности для непрерывной случайной релеевской переменной определяется формулой (15.15).

а) Найдите выражение для функции распределения, как это описано в разделе 1.5.5.

б) Используйте функцию распределения для определения процента времени, в течение которого уровень сигнала будет на 15дБ ниже среднеквадратического значения для сигнала, переданного по каналу мобильной радиосвязи, испытывающему релеевское замирание.

в) Повторите п. б для уровня сигнала, который на 5дБ ниже средне-квадратического.

15.2. Сигнал в системе мобильной радиосвязи расширяется во времени. Скорость передачи символов Rs=2010³ символов/с. Измерения в канале показывают, что средняя избыточная задержка распространения равна 10 мкс, а второй момент избыточной задержки равен 1,810^-10 с².

а) Вычислите ширину полосы когерентности f0, если она определена как интервал частот, в пределах которого комплексная передаточная функция имеет корреляцию не меньше 0,9.

б) Повторите п. а, если f0 определена как интервал, имеющий корреля-цию не меньше 0,5.

в) Определите, будет ли сигнал подвергаться частотно-селективному замиранию.

15.3. Рассмотрим канал, профиль плотности мощности которого состоит из трех импульсных функций со следующей мощностью и следующим расположением временной задержки: -20дБ при 0 мкс, 0дБ при 2 мкс и -10дБ при 3 мкс.

а) Вычислите среднюю избыточную задержку.

б) Вычислите второй момент избыточной задержки.

в) Вычислите среднеквадратический разброс задержек.

г) Оцените ширину полосы когерентности (соответствующую кор-реляции не менее 0,9).

д) Вычислите приблизительное значение частоты передачи, если приемник расположен на самолете, движущемся со скоростью 800 км/ч, а время, требуемое для пересечения расстояния, равного половины длины волны, равно 100 мкс.

15.4. Дана система мобильной радиосвязи с несущей частотой fc=900 МГц и доплеровской частотой fd=50 Гц. Предполагается, что применяется модель плотного размещения рассеивающих элементов.

а) Изобразите график доплеровской плотности спектральной мощности S(v) в интервале fc fd (используйте порядка 10 точек).

б) Объясните поведение S(v) на границах.

в) Вычислите время когерентности T0, предполагая, что отклик канала на синусоиду дает корреляцию не менее 0,5.

15.5. Для каждой из перечисленных ниже категорий замирания назовите приложение, обычно подпадающее под эту категорию. Дайте количественное обоснование.

а) Частотно-селективное, быстрое замирание.

б) Частотно-селективное, медленное замирание.

в) Амплитудное замирание, быстрое замирание.

г) Амплитудное замирание, медленное замирание.

15.6. а) Как связаны профиль плотности мощности сигнала, характеризующийся среднеквадратической задержкой , и доплеровская спектральная плотность мощности, характеризующаяся шириной полосы замирания fd?

б) Как связаны частотная корреляционная функция, которая характеризуется шириной полосы когерентности f0), и временная корреляционная функция, которая характеризуется временем когерентности Т0?

15.7. Рассмотрим узкополосные системы мобильной связи для применения внутри помещений, которые характеризуются профилем плотности мощности, состоящим из четырех импульсных функций со следующей мощностью и следующим расположением временной задержки: 0 дБ при 0 нс, -3 дБ при 100 нс, -3 дБ при 200 нс и -6 дБ при 300 нс. Какую максимальную скорость передачи символов может поддерживать такая система без использования эквалайзера? Для нахождения ширины полосы когерентности воспользуйтесь определением, в котором фигурирует корреляция тонов 0,5.

15.8. Рассмотрим систему мобильной радиосвязи, использующую модуляцию QPSK при скорости передачи 24,310³символов/с и несущей частоте 1900 МГц. Какова наибольшая допустимая скорость транспортных средств, использующих такую систему, если требуется, чтобы изменения фазы в результате спектрального расширения (доплеровского расширения) не превышали 5°/символ?

15.9. Чтобы чередование обеспечивало значимое разнесение во времени, эмпирическое правило требует, чтобы рабочий интервал соответствующего устройства Тп был, по крайней мере, в десять раз больше времени когерентности канала Т0. Покажите график зависимости Тп от частоты (отобразите по три значения частоты: 300 МГц, 3 ГГц и 30 ГГц) для следующих пользователей мобильных телефонов.

а) Пешеход, идущий со скоростью 1 м/с.

б) Скоростной поезд, движущийся со скоростью 50 м/с

в) Если телефон используется для общения в реальном времени, то какая из шести точек на графике описывает случай, когда можно достичь значимого разнесения во времени при использовании рабочего интервала устройства чередования, ровно в десять раз превышающего Т0?

г) Какие общие выводы можно сделать?

15.10. Ширина полосы передаваемого сигнала равна 5 кГц, сигнал распространяется по каналу с полосой когерентности 50 кГц. Очевидно, что это один из примеров каналов с амплитудным замиранием. Объясните, как такой канал может время от времени подвергаться частотно-селективному замиранию.

15.11. Рассмотрим систему мобильной радиосвязи TDMA с несущей частотой 1900 МГц, которая работает на поездах при скоростях 180 км/ч. Для изучения импульсной характеристики канала с целью обеспечения выравнивания в передачу каждого пользователя в дополнение к информационным битам вносятся настроечные биты. Необходимо, чтобы настроечная последовательность состояла из 20 бит, при этом данное число не должно превышать 20% от общего количества бит, также настроечные биты должны внедряться в данные, по крайней мере, каждые Т0/4 с. Предполагая двоичную модуляцию, определите наименьшую скорость передачи, при которой эти требования удовлетворялись бы без быстрого замирания.

15.12. а) В конце 80-х в Японии была разработана система PHS (Portable Handyphone System — персональная система переносных телефонов). Спецификация PHS задает разнесение несущих, равное 300 кГц. Восприимчив ли этот стандарт к частотно-селективному замиранию в среде, в которой канал обладает среднеквадратическим разбросом задержек порядка 300 нс?

б) Стандарт телефонов DECT (Digital Enhanced Cordless Telephone —цифровые расширенные беспроводные телекоммуникации) был разработан для информационного обмена высокой плотности и ближней связи (внутри помещений). Спецификация DECT задает разнесение несущих, равное 1,728 МГц. Предполагается, что среднеквадратический разброс задержек равен 150 нс. Определите, нужно ли включать в схему приемника DECT эквалайзер.

15.13. Рабочий интервал устройства чередования должен, по крайней мере, в 10 раз превышать время когерентности канала, чтобы дать существенное разнесение по времени в мобильной системе радиосвязи. Рассмотрите использование такого устройства при проектировании системы мобильной связи, работающей на частоте 1 ГГц и предназначенной для пешеходов, идущих со скоростью 0,5 м/с. Насколько большим должен быть интервал? Подходит ли это для системы речевой связи реального времени?

15.14. Какое максимальное отношение рабочего интервала устройства чередования ко времени когерентности можно использовать в следующих случаях, если суммарный интервал задержки передатчика и приемника необходимо удержать ниже 100 мс.

а) Скорость замирания в канале равна 100 Гц.

б) Скорость замирания в канале равна 1000 Гц.

15.15. Системы мобильной связи сконструированы так, чтобы поддерживать скорость передачи данных, равную 200 Кбит/с, используя при этом модуляцию QPSK и несущую частоту 1900 МГц. Они предназначены для использования в транспортных средствах, которые обычно движутся со скоростью 96 км/ч.

а) Какое изменение фазового угла на символ можно ожидать?

б) Чему будет равно на символ, если скорость передачи уменьшится до 100 Кбит/с?

в) Повторите п. б для скорости 48 км/ч.

г) Сделайте общие выводы для данного случая.

15.16. Среднеквадратический разброс задержек в канале, испытывающем замирание вследствие многолучевого распространения, равен = 10 мкс, а доплеровское расширение равно fd = 1 Гц. Длительность широкополосного импульса принимается равной Тs = 1 мкс.

а) Чему равна ширина полосы когерентности канала?

б) Чему равно время когерентности канала?

в) Как можно было бы классифицировать канал относительно частот-ной избирательности и скорости замирания.

г) Как можно было бы изменить длительность импульса (скорость передачи данных), чтобы ослабить эффекты замирания?

15.17. В мобильных системах радиосвязи схема, основанная на фазовой модуляции, чрезвычайно подвержена фазовым искажениям. Этих искажений можно избежать, если скорость передачи сигнала превышает скорость замирания, по меньшей мере, в 100 раз [27]. Рассмотрим радиосистему, работающую на несущей частоте 1900 МГц и движущуюся со скоростью 96 км/ч. Какой должна быть наименьшая скорость передачи символа в такой системе, чтобы избежать искажений вследствие быстрого замирания?

15.18. Рассмотрим систему мобильной связи, обладающую кадровой структурой и распределением временных слотов (рис. 315.1).

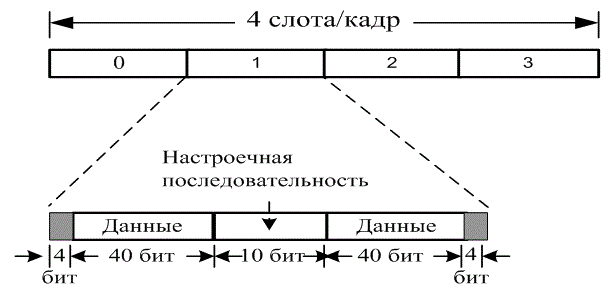
Рис. 315.1. Формат кадра ТDМА

На каждый кадр приходится 4 временных слота; каждому пользователю отводится один слот на кадр. Каждый слот содержит 98 бит, как это показано на рис. 315.1. При передаче сигнала используется модуляция QPSK с несущей частотой 700 МГц. Скорость передачи равна 33,610³ символов/с, а ширина полосы пропускания равна 47кГц. Система должна нормально функционировать при скоростях до 100км/ч. Измерения, проводимые в физическом канале, показали, что типичное среднеквадратическое значение разброса задержек составляет порядка 4 мкс.

а) Будут ли в канале эффекты ухудшения характеристик вследствие быстрого замирания, если предположить, что настроечная последовательность позволяет оценить импульсную характеристику канала в течение каждого сегмента времени?

б) Будет ли такая конструкция подвергаться ухудшению характеристик вследствие частотно-селективного замирания?

15.19. Общая допустимая задержка переданных данных в отдельном канале мобильной радиосвязи ограничена величиной 340 мс. Скорость передачи данных равна 19,210³ символов/с, данные при этом чередуются с целью разнесения во времени. Задержки, характерные для системы, показаны в табл. 315.1.

Таблица 315.1. Значение задержек в мс

Задержка, Т	Значение (в мс)
Кодер Модулятор Канал Демодулятор Декодер	2 10 0,3 25 2108/fclk

Задержка в миллисекундах для декодера дана в виде 210⁸/fclk, где fclk - тактовая частота декодера. Вычислите минимальную тактовую частоту декодера, требуемую при следующих рабочих диапазонах устройства чередования.

а) 100 бит

б) 1000 бит

в) 2850 бит

г) Какие можно сделать выводы относительно поведения тактовой частоты декодера в результате увеличения размера рабочего интервала устройства?

15.20. Рассмотрим систему мобильной связи с ортогональной FDM (OFDM), которая предназначена для работы в транспортных средствах (со скоростью 80 км/ч в городской среде) и обладает шириной полосы когерентности 100 кГц. Несущая частота равна 3 ГГц, при этом требуется, чтобы данные передавались при скорости 102410³ символов/с. Выберите подходящую схему поднесущих для следующих целей: 1) избежать использования эквалайзера и 2) минимизировать любые эффекты, вызванные быстрым замиранием. Схема должна определять, сколько необходимо поднесущих, насколько далеко они должны быть разнесены по частоте и какое должно использоваться значение отношения скорости передачи символов на поднесущую.

15.21. Системы мобильной радиосвязи используют передачу сигналов со спектром, расширенным методом прямой последовательности (direct-sequence spread-spectrum — DS/SS), для ослабления следствий того, что полученный сигнал имеет два компонента: прошедший по прямому пути и пришедший после отражения. Отраженный путь на 120 м длиннее прямого. Какой должна быть скорость передачи элементарного сигнала, чтобы такая система ослабляла эффект многолучевого распространения?

15.22. Общеизвестно, что передача сигналов со спектром, расширенным методом прямой последовательности (direct-sequence spread-spectrum — DS/SS), может использоваться кик метод борьбы с вызванной каналом ISI в частотно-селективных каналах. Тем не менее, если рассмотреть рис. 15.25 в определенный момент времени, скажем , то будет присутствовать интерференция между элементарными сигналами. Нужно ли использовать дополнительные методы выравнивания, чтобы преодолеть интерференцию на уровне элементарных сигналов? Объясните.

15.23. Схемы CDMA и ТDМА уникальны в том смысле, что каждая из этих схем множественного доступа имеет свои средства борьбы с замиранием. От каких типов ухудшения характеристик «естественным образом» защищает каждая схема?

15.24. Рассмотрим схему разнесения, состоящую из четырех каналов, как показано на рис. 315.2. Каждый канал отвечает за прохождение сигналов r(t), независимо замирающих по Релею. В определенный момент времени полученный сигнал может быть выражен в виде четырехмерного вектора r = [r1, r2, r3, r4], где ri - напряжение в канале i. Кроме того, усиление в каждом из каналов можно выразить через четырехмерный вектор G = [G1, G2, G3, G4], где Gi - описывает усиление напряжения в канале i. Рассмотрим момент времени, в который измеренное значение r было равно [0,87, 1,21, 0,66, 1,90], а соответствующее усиление G — [0,5, 0,8, 1,0,0,8]. Средняя мощность шума в каждом канале N равна 0,25.

а) Вычислите SNR сигнала, поступающего на детектор.

б) Можно показать [1], что SNR максимально, когда все Gi - равны r/N. Используя этот факт, определите максимально достижимое SNR.

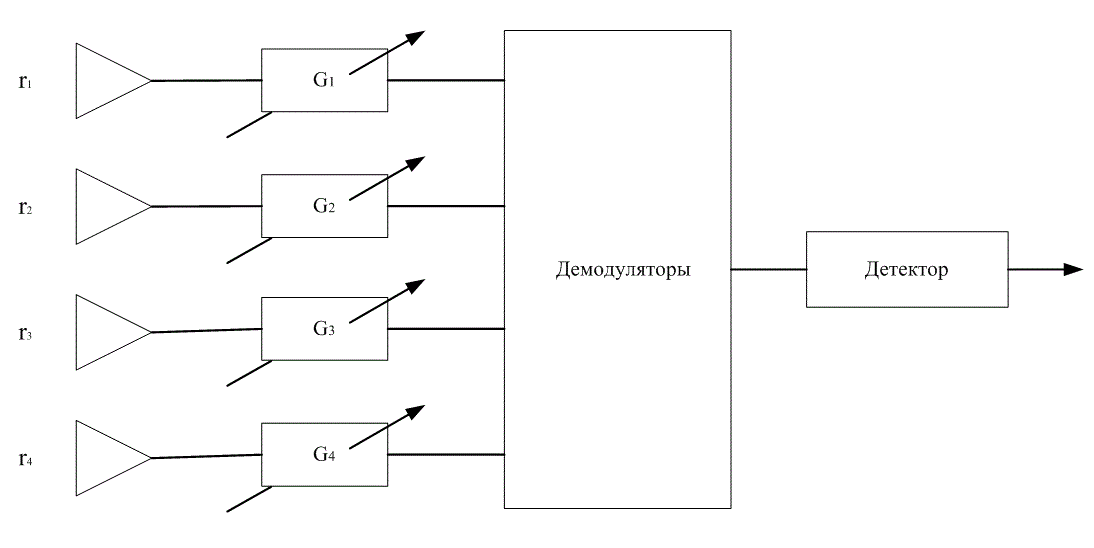
Рис. 315.2. Приемник с разнесением на четыре канала

15.25. В системе для улучшения значения SNR приемника используется разнесение каналов. Предполагается, что каждый канал получает независимо замирающий релеевский сигнал. Приемник должен удовлетворять следующему требованию: вероятность получения всеми каналами сигнала с SNR, меньшим некоторого порогового значения, равна 10^-4, где пороговое значение принято равным 5 дБ, а среднее SNR равно 15 дБ.

а) Вычислите количество каналов разнесенного приема М, необходи-мых для того, чтобы приемник удовлетворял этому условию.

б) Основываясь на результатах п. а, вычислите вероятность получения во всех каналах SNR >5дБ.

15.26. В приемнике с двумя каналами используется схема разнесения. Из каждого канала было получено следующее.

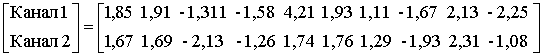
В первой строке показаны значения напряжений в первом канале, а во второй строке — напряжения во втором канале. Каждый столбец соответствует определенному моменту времени. Считается, что средняя мощность шума в каждом канале равна 0,25 Вт, также предполагается, что упомянутые выше значения преобразованы в синфазные с последующим объединением методами максимального отношения и равного усиления. Мгновенное усиление напряжения, предоставляемое делителем для каналов 1 и 2, равно G1 = 1,2 и G2= 1,4. Кроме того, разнесение с обратной связью предполагает, что пороговое значение SNR нужно установить равным 5 дБ.

Вычислите, выход, какого канала будет подан на детектор, если используются следующие методы разнесения.

а) Выборочный.

б) С обратной связью.

Вычислите величину SNR, которую имеет сигнал, поданный на детектор, если используются следующие методы разнесения.

а) Максимального отношения.

б) Равного усиления.

15.27. Отклик канала на идеальный положительный или отрицательный импульс расширяется в три раза, как это показано на рис. 315.3. Таким образом, для последовательности переданных импульсов полученный сигнал состоит из суперпозиции L(=3) вкладов (сегменты от трех импульсов) — текущий импульс плюс память о двух предыдущих импульсах. Используйте диаграмму решетчатого кодирования для описания вызванной каналом ISI и пометьте каждую ветвь решетки значениями напряжения, являющимися результатом перехода. Изначально система была очищена до состояния 00 путем передачи двух отрицательно поляризованных импульсов. Затем рассмотрите передачу последовательности 11011с использованием идеальных импульсов, изображенных на рис. 315.3. Определите амплитуду полученного искаженного сигнала и покажите его путь по решетчатой диаграмме. Подсказка: эта двоичная система с конечным числом состояний имеет 2^L-1 состояний. Воспользуйтесь миллиметровкой для вычисления суперпозиции, необходимой для представления искаженных сигналов, характеризующих канал. Построение решетчатой диаграммы описано в разделе 7.2.3. Единственное замечание: здесь вместо кодовых битов используются уровни напряжения.

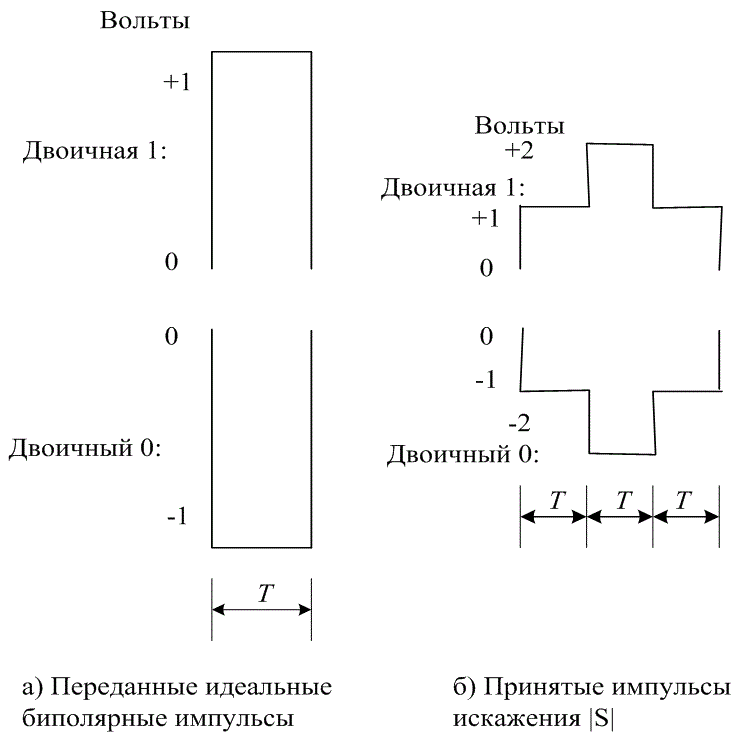
Рис. 315.3

15.28. Используйте характеристики канала и настроечную последовательность, описанную в задаче 15.27, и добавьте шумовое напряжение, равное {+1 -1 +1 -1 +1}, для получения искаженного сигнала. Применяйте диаграмму решетчатого декодирования для иллюстрации того, как алгоритм декодирования Витерби используется в этом процессе выравнивания, и приведите вычисления, дающие первый бит сообщения. Подсказка: процесс подобен декодированию битов, кодированных сверточным кодом, где вместо кодовых битов используются уровни напряжения.

15.29. В мобильных системах связи для борьбы с эффектами замирания используется эквалайзер Витерби. Скорость передачи равна 16010³ символов/с, для модуляции используется схема BPSK. Дисперсия сигнала, являющаяся результатом вызванной каналом ISI, равна 25 мкс.

а) Вычислите приблизительный объем памяти L0 в битовых интервалах, который необходимо включить в эквалайзер Витерби.

б) Каким должен, быть объем памяти, чтобы удвоить скорость передачи символов?

Вопросы

15.1. Какие два механизма характеризуют мелкомасштабное замирание? Объясните, как временное и частотное описание этих механизмов связано через Фурье-преобразование и отношение дуальности (см. разделы 15.2-15.4).

15.2. Какая разница между райсовским и релеевским замиранием (см. раздел 15.2.2)?

15.3. Определите следующие параметры: среднеквадратический разброс задержек, ширина полосы когерентности, время когерентности, доплеровское расширение. Как они связаны между собой (см. разделы 15.3 и 15.4)?

15.4. Какие две категории ухудшения характеристик характеризуют рассеяние сигнала по времени, а какие две — нестационарную природу канала (см. разделы 15.3 и 15.4.)?

15.5. Почему два основных механизма замирания, характеризующих мелкомасштабное замирание, рассматриваются независимо друг от друга (см. раздел 15.4.1.1)?

15.6. Почему искажение сигнала, вызванное замиранием, является более серьезным эффектом искажения, чем уменьшение SNR(см. раздел 15.5)?

15.7. Какие методы применяются для борьбы с частотно-селективном замиранием? Какие методы используются для борьбы с быстрым замиранием (см. раздел 15.5)?

15.8. Какие существуют способы разнесения сигнала (см. раздел 15.5.3)?

15.9. Если между передатчиком и приемником отсутствует движение, какой рабочий интервал устройства чередования нужен для зашиты от быстрого замирания (см. раздел 15.5.6)?