5.1. Уравнение однородной линии

5.2. Вторичные параметры цепи

5.3. Оптимальное соотношение параметров кабельных линий

5.4. Способы увеличения индуктивности кабельных линий

5.1. Уравнение однородной линии

При определённых условиях первичные параметры полностью характеризуют электрические свойства линейных цепей связи. Однако в отличии от сосредоточенных параметров они распределены по всей длине линии.

Рассмотрим однородную цепь связи с первичными параметрами: R, L, C, и G.

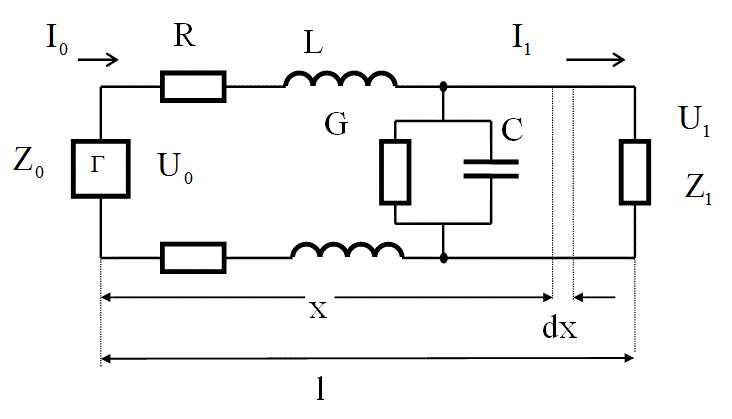
Рис.1

В начале цепи имеется генератор с сопротивлением , в конце - нагрузка . Соответственно - напряжение и ток в начале цепи; - напряжение и ток в конце цепи.

Выделим на расстоянии x от начала цепи бесконечно малый участок dx. Обозначим ток, протекающий по элементу цепи dx, через I и напряжение между проводами через U. Тогда падение напряжения на участке dx будет равно:

. (5.1)

Утечка тока на участке:

(5.2).

Продифференцируем первое уравнение

(5.3).

Подставив (2) в (3) получим:

(5.4).

Обозначив , получим:

. (5.5)

Как известно, решение данного уравнения имеет вид:

. (5.6)

Продифференцировав (6) и подставив результат вместо правой части выражения (1) получим:

. (5.7)

Обозначив , получим в окончательном виде:

.

Таким образом имеем систему уравнений из двух неизвестных:

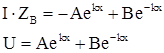(5.8)

Для нахождения A и B воспользуемся значениями тока и напряжения в начале цепи (при x=0) и . Тогда уравнения примут вид:

.

Отсюда

; . (5.9)

Подставив значения A и B в (8) получим:

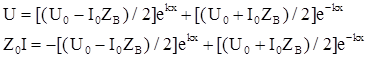. (5.10)

Произведя соответствующие преобразования, имея в виду, что и , получим значения и в любой точке цепи x:

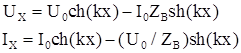. (5.11)

Эти уравнения справедливы при любых нагрузках на концах цепи, однако, передача сигналов с наименьшими потерями достигается при согласованных нагрузках, т.е. . При этом уравнения преобразуются к виду:

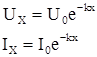. (5.12)

5.2. Вторичные параметры цепи

Из приведённых выше формул следует, что распространение энергии по линии, ток и напряжение в любой точке цепи обусловлены в первую очередь параметрами и .

Сравним выражение (5.12) с выражением (2.13) в лекции 2. По аналогии с (2.13) физический смысл (5.12) плоская волна бегущая по направлению к концу линии. В таком случае здесь также коэффициент распространения, состоящий из действительной и мнимой части, имеющих аналогичный физический смысл. Выше нами определена зависимость характеристического сопротивления от параметров линии

(5.13)

где - коэффициент затухания;

β - коэффициент фазы.

Уравнения для токов и напряжений можно представить в следующем виде:

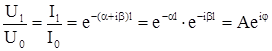. (5.14)

Модуль этого выражения характеризует уменьшение абсолютного значения тока или напряжения при прохождении по линии длиной l. Угол характеризует изменение угла фазового набега на этом же участке линии длиной l.

Расчетные формулы для и через первичные параметры нетрудно получить из (5.13):

(5.15)

(5.16)

(Выражение (5.16) получаем возведя в квадрат обе половины выражения (5.13) и прировняв действительные части).

Сумма выражений (5.15) и (5.16) даёт выражение для , разность - для :

(5.17);

(5.18).

Следует обратить внимание на размерность (Нп/км; 1Нп=8.686дБ) и (рад/км; 1рад=57.3⁰). (Непер - единица при натуральном логарифме отношения. дБ - десятичный логарифм отношения)

Выражение для также было введено ранее:

. (5.19))

Проанализируем его размерность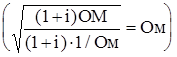. Так как определяется распределёнными параметрами R,G,L и C, то по аналогии с (3.) его следует считать характеристическим (волновым) сопротивлением линии. Действительно для идеальной линии где выражение для будет совпадать с выражением для характеристического сопротивления контура .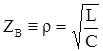

В общем случае характеристическое (волновое) сопротивление является также комплексной величиной и может быть представлено в виде: .

Оба характеристическое сопротивление и коэффициент распространения широко используются для оценки эксплуатационно-технических качеств линий связи и называются вторичными параметрами линии.

5.3. Оптимальное соотношение параметров кабельных линий

Как видно вторичные параметры линии существенным образом зависят от частоты сигнала.

1. При постоянном токе: ; ; ; .

2. В диапазоне относительно низких (тональных) частот:

, .

и - рассчитываются по полным формулам;

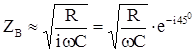, где ; .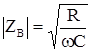

3. В диапазоне средних частот вторичные параметры рассчитываются по полным формулам.

4. В диапазоне высоких частот:, .

, .

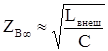Определим аналитическое выражение для коэффициента затухания для чего преобразуем выражение (5.13) следующим образом(нетрудно убедится, что простая подстановка в (5.17) результата не даёт):

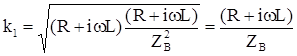, (5.20)

. (5.21)

Так как оба выражения (16) и (17) равноценны, то

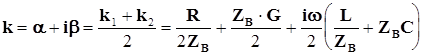. (5.22)

Очевидно действительная часть выражения (5.22) и есть коэффициент затухания. При этом

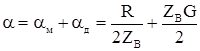. (5.23)

Подставив в (5.23) выражение для волнового сопротивления на высоких частотах окончательно получим:

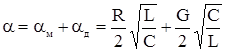. (5.24)

Причем первый член суммы определяет затухание за счет потерь в проводнике, а второй в диэлектрике.

Одной из актуальных проблем кабельной техники является увеличение дальности связи без дополнительного расхода цветных металлов. Особенно это актуально для протяженных линий и высоких частот передачи. С этой целью идет постоянное совершенствование аппаратуры связи и электрических свойств кабелей связи. Прежде всего для этого необходимо уменьшить коэффициент затухания . Как видим затухание может быть снижено уменьшением R и G, но это крайне затруднительно, т.к. значения этих величин регламентированы допустимым расходом меди (диаметром жилы) и качеством диэлектрика. Уменьшение ёмкости С связано с необходимостью увеличения расстояния между жилами кабеля, т.е. увеличения его габаритов, что также не целесообразно. Остается возможность увеличения индуктивности L. Минимальное значение достигается при таком L, при котором достигается равенство 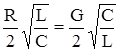. Отсюда

. (5.25)

В кабелях существующих типов R и C превосходят L и G (RC>>LG). Поэтому увеличение индуктивности приводит к уменьшению затухания , но до некоторых частот. С возрастанием частоты увеличивается проводимость изоляции и на определенной частоте наступает равенство без искусственного повышения L. Для симметричных кабелей связи эта частота лежит в пределах кГц.

5.4. Способы увеличения индуктивности кабельных линий

Увеличить индуктивность кабельных цепей и соответственно снизить их затухание можно следующими спосбами:

• пупенизацией кабеля;
• крарупизацией кабеля;
• биметаллизацией кабеля;
• использованием магнитодиэлектрика.

Крарупизация состоит в навивке на токопроводящую жилу тонкой проволоки или ленты из стали, пермаллоя или другого сплава с большой магнитной проницаемостью.

Биметаллизация состоит в том, что на токопроводящую жилу электролитическим путём наносится тонкий слой железа (мкм).

В обеих случаях благодаря этому вокруг медной жилы образуется магнитопроводящая среда увеличивающая магнитный поток и соответственно индуктивность кабельной цепи.

Такого же эффекта можно достигнуть, если использовать в качестве слоя диэлектрики, обладающие большой магнитной проницаемостью. В этом случае достигается двойной эффект: изоляция жилы кабеля и увеличения его индуктивности.

Однако наибольшее распространение получил способ пупинезации кабельных цепей. Он состоит в том, что для увеличения индуктивности в кабель через определённые расстояния (шаг пупенизации) включают катушки индуктивности, называемые в честь автора их предложившего (Пупина - американский инженер) пупиновскими. В существующих системах пупенизации кабелей дальней связи: шаг пупенизации км, а индуктивность катушек мГн.

Звеном пупенизации называют участок линии протяженностью в один шаг S и с одной катушкой, обладающей индуктивностью . Пупиновская катушка представляет собой замкнутый сердечник из ферромагнитного материала круглого или овального сечения с обмотками из медной изолированной проволоки (см. Рис. ). Катушка помещается в металлический чехол, служащий ЭМ экраном и защитой от механических повреждений.

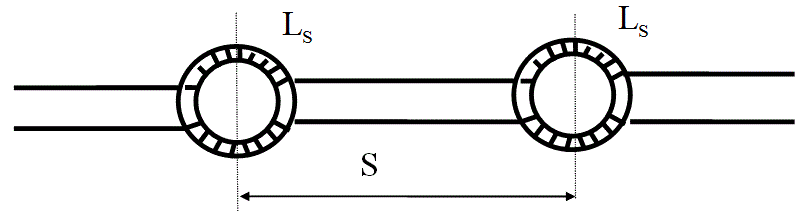
Недостаток: пупенизированная линия пропускает с малым затуханием только нижние частоты попадающие в «полосу прзрачности» и задерживает высокие частоты, т.е. ведёт себя как фильтр низких частот.