Для того чтобы найти среднее количество информации T(s,x), передаваемое сигналом на интервале Т, необходимо рассмотреть n=2FT отсчетов непрерывного сигнала на входе канала: s1; s2;.., sn и на выходе канала: x1; x2;..;хп. В этом случае по аналогии с выражениями (6.69) и (6.72) можно записать

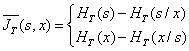(6.78)

где

s, sbx, х„

Энтропии HT(s) и HT(s/x) описываются аналогичными выражениями, только всюду необходимо поменять местами переменные s и х Скорость передачи информации по непрерывному каналу находится как предел:

(6.79)

Максимальная скорость передачи в непрерывном канале определяет его пропускную способность

(6.80)

где максимум определяется по всем возможным ансамблям входных сигналов s.

Вычислим пропускную способность непрерывного канала, в котором помехой является аддитивный шум. w(t), представляющий собой случайный эргодический процесс с нормальным распределеннием и равномерным спектром. Средние мощности сигнала я шума ограничены величинами Рси Р, а ширина их спектра paвна F.

Согласно выражениям (6,80) и (6.78) имеем

(6.81)

Прежде всего найдем величину НT (x/s). С этой целью рассмотрим энтропию шума для одного отсчета (6.74), которая с учетом соотношения p(s, x)=p(s)p(x/s) может быть представлена в следующем виде:

(6.82)

При заданном значении s сигнал на выходе канала x=s+w полностью определяется аддитивным шумом w. Поэтому

(6.83)

где рш(х—s) — плотность вероятности шума.

Подставляя (6.83) в (6.82) и заменяя переменную х на , т. е. подставляя вместо х сумму s +, можем записать

Принимая во внимание, что, получим

Следовательно, условная энтропия H(x/s) при аддитивном шуме зависит только от его распределения рш(), что и объясняет термин энтропия шума. Следовательно, на интервале Т

(6.84)

где n=2FT.

Значения шума с равномерным спектром некоррелированы между собой в моменты отсчетов, разделенные интервалом

Отсутствие статистической взаимосвязи между отсчетами шума позволяет представить энтропию суммы п отсчетов шума (6.84) как сумму энтропий отдельных отсчетов, которые вследствие стационарности шума равны между собой. С учетом этих соображений можно записать

Поскольку отсчеты шума статистически независимы, а каждый из них распределен по нормальному закону, то энтропия HT(w) максимальна и в соответствии с (6.77) равна:

(6.85)

где вместо подставлено .

При данной величине HT(x/s) = HT(w) пропускная способность (6.81) отыскивается путем максимизации НТ(х). Максимум НТ(х), очевидно, имеет место, когда сигнал х так же, как и шум, характеризуется нормальным распределением и равномерным спектром.

Отсюда

(6.86)

Здесь предполагается, что сигнал s и помеха w независимы, поэтому мощность сигнала х равна сумме мощностей. Подставляя (6.85) и (6.86) в (6.81), окончательно получим

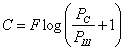(6.87)

Так как х и w имеют нормальное распределение, то сигнал s=x-w также должен иметь нормальное распределение. Отсюда следует важный вывод: для того чтобы получить максимальную скорость передачи информации, необходимо применять сигналы с нормальным распределением и равномерным спектром.

Формула (6.87), впервые выведенная Шенноном, играет важную роль в теории и технике связи, Она показывает те предельные возможности, к которым следует стремиться при разработке современных систем связи. Так как при равномерном спектре мощность шума определяется произведением Pш=N0F, то ф-лу (6.87J можно записать в другом виде

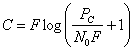(6.88)

С увеличением F пропускная способность монотонно возрастает стремится, как показано на рис. 6.4а, к величине

(6.89)

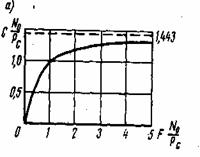
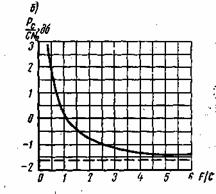
Рис. 6.4. Зависимость пропускной способности С от полосы пропускания F в непрерывном канале

Нa рис. 6.46 зависимость (6.88) изображена в другой нормировке, из которой следует, что при фиксированных значениях пропускной способности С и энергетического спектра шума N существует обратная зависимость между Рси F. Иными словами, допускается уменьшение мощности сигнала за счет расширения его спектра.

Формулу (6.87), выведенную для равномерных спектров сигнала и шума, можно распространить и на случай неравномерных спектров. С этой целью в окрестностях некоторой частоты выберем достаточно узкую полосу, в которой спектры сигнала Gc(f) и шума Gш(f) будут постоянными. Тогда для этой полосы в соответствии с (6.87) /пропускная способность будет равна:

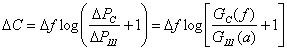(6.90)

где и

Полная пропускная способность вычисляется как интеграл от (6.90) по всем частотам спектра сигнала

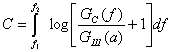(6.91)

Можно показать, что при заданном спектре шума Gш(f) и ограниченной мощности сигнала максимум С имеет место в случае выполнения условия

(6.92)

т. е. мощность сигнала должна возрастать на тех частотах, где уменьшается мощность шума и наоборот. Можно также поставить вопрос: если выполняется условие (6.92), то при каком спектре шума получается минимальная пропускная способность? Оказывается, что этому условию удовлетворяет равномерный спектр, т. е. спектр белого шума. Таким образом, белый шум, уменьшающий в наибольшей степени пропускную способность, является самым опасным видом помех.

Рассмотрим теперь вопрос о производительности источника непрерывных сообщений и о влиянии на качество их передачи помех, действующих в канале связи. При отсутствии каких-либо ограничений, накладываемых на непрерывные сообщения, количество содержащейся в них информации согласно (6.1) равно бесконечности:

Поэтому источник таких сообщений обладает бесконечной производительностью (6.25). Для того чтобы количество информации и производительность источника приобрели определенный смысл и стали конечными величинами, необходимо рассматривать непрерывное сообщение u(t) с учетам точности его оценки. Последняя, в частности, определяется погрешностью приборов, с помощью которых измеряется или регистрируется непрерывное сообщение. Обычно погрешность количественно оценивается среднеквадратичным отклонением приближенного непрерывного сообщения u*(t) от его точного значения u(t):

Нетрудно понять, что чем меньше , тем большее количество информации в среднем содержится в u*(t) относительно u(t) и тем выше производительность источника.

Количество информации на выходе источника при >0 по аналогии с (6.68) определяется как

(6.93)

Для ограниченной погрешности всегда можно найти такой способ воспроизведения u(t) посредством и* (t), а следовательно, такое распределение р'(и, и*), при котором выражение (6.93) достигает наименьшего значения. Распределение р'(и, и*) является наиболее выгодным, так как оно позволяет при заданной .погрешности воспроизводить u(t), используя минимальное количество информации. Наименьшее значение J(и, и*) при называется эпсилон-энтропией

(6.94)

Тогда производительность источника непрерывных сообщений

Для непрерывного канала с пропускной способностью С, на вход которого подключается источник, обладающий производительностью , Шенноном была доказана следующая теорема.

Если при заданной погрешности оценки сообщений источника его производительность <C, то существует способ кодирования, позволяющий передавать все непрерывные сообщения источника с ошибкой в воспроизведении на выходе канала, сколь угодно мало отличающейся от .

Иначе говоря, дополнительная неточность в воспроизведении сообщения v(t) на выходе канала, обусловленная воздействием помех, может быть сделана весьма незначительной, т. е.

, где — сколь угодно малая величина.

Скорость передачи информации по каналу в конечном счете определяется скоростью потока информации на выходе приемника

где НТ(и) — энтропия принятого сообщения v(t), HT(w*) — энтропия шума на выходе приемника. Если считать, что сообщение v(t) и помеха w*(t) на выходе приемника имеют нормальное распределение и равномерный спектр, то

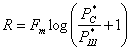(6.95)

Здесь Fm — ширина спектра частот принимаемого сообщения, обычно равная полосе пропускания приемника по низкой частоте; P* — средняя мощность принятого сообщения v(t); Р* — средняя мощность шума на выходе приемника.