6.6.1. Оценка возможностей кода
6.6.1. Оценка возможностей кода
Нормальную матрицу можно представлять как организационный инструмент, картотеку, содержащую все возможные 
записи в пространстве n-кортежей, в которой ничего не упущено и не продублировано. На первый взгляд может показаться, что выгода от использования этого инструмента ограничена малыми блочными кодами, поскольку для кодов длиной более n=20 пространство n-кортежей насчитывает миллионы элементов. Впрочем, даже для больших кодов нормальная матрица позволяет определить важные исходные характеристики, такие как возможные компромиссы между обнаружением и исправлением ошибок и пределы возможностей кода в коррекции ошибок. Одно из таких ограничений, называемое пределом Хэмминга [7], описывается следующим образом.
Количество бит четности: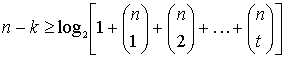 
(6.52,а)
или
Количество классов смежности: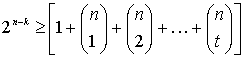
(6.52,6)
Здесь величина 
, определяемая уравнением (6.16), представляет число способов выбора из п бит j ошибочных. Заметим, что сумма членов уравнения (6.52), находящихся в квадратных скобках, дает минимальное количество строк, которое должно присутствовать в нормальной матрице для исправления всех комбинаций ошибок, вплоть до t-битовых ошибок. Неравенство определяет нижнюю границу числа п-k бит четности (или 
классов смежности) как функцию возможностей кода в коррекции t-битовых ошибок. Аналогичным образом можно сказать, что неравенство дает верхнюю границу возможностей кода в коррекции t-битовых ошибок как функцию числа n-k бит четности (или классов смежности). Для обеспечения возможности коррекции t-битовых ошибок произвольных линейных блочных кодов (п, k) необходимым условием является удовлетворение предела Хэмминга.
Чтобы показать, как нормальная матрица может обеспечить визуальное представление этого предела, возьмем в качестве примера код БХЧ (127,106). Матрица содержит все 
= 2127= 1,70 х 1038n- кортежей пространства. Верхняя строка матрицы содержит = 2106 = 8,11 x 1031 кодовых слов; следовательно, это число столбцов в матрице. Крайний левый столбец содержит 
2 097 152 образующих элемента классов смежности; следовательно, это количество строк в матрице. Несмотря на то что число n-кортежей и кодовых слов просто огромно, нас не интересует конкретный вид каждого элемента матрицы. Основной интерес представляет количество классов смежности. Существует 2 097 152 класса смежности и, следовательно, 2 097 151 ошибочная комбинация, которую способен исправить, этот код. Далее показано, каким образом это число классов смежности определяет верхний предел возможностей кода в коррекции t-битовых ошибок.
Поскольку каждое кодовое слово содержит 127 бит, существует 127 возможностей допустить ошибку в одном бите. Рассчитываем количество возможностей появления двух ошибок — 
= 8 001. Затем переходим к трехбитовым ошибкам, поскольку ошибки, упомянутые выше, — это лишь незначительная часть всех 2 097 151 ошибочных комбинаций. Итак, существует 
= 333 375 возможностей совершить трехбитовую ошибку.
Эти расчеты приведены в табл. 6.3; там же показано, что нулевая ошибочная комбинация требует наличия первого класса смежности. Затем перечислены требования одно-, двух- и трехбитовых ошибок. Также показывается количество классов смежности, необходимое для коррекции каждого типа ошибок, и общее количество классов смежности, необходимых для коррекции ошибок всех типов, вплоть до требуемого типа ошибки. Из этой таблицы можно видеть, что код (127,106) способен исправить все комбинации, содержащие 1, 2 или 3 ошибочных бита, причем это составляет только 341504 из 2 097 152 возможных классов смежности. Неиспользованные 1 755 648 строк говорят о больших потенциальных возможностях в коррекции ошибок, чем было использовано. Действительно, в матрицу можно попытаться втиснуть все возможные 4-битовые ошибки. Но при взгляде на табл. 6.3 становится совершенно ясно, что это невозможно, поскольку, как показывает последняя строка таблицы, число оставшихся в матрице классов смежности значительно меньше общего числа классов смежности, требуемого для коррекции 4-битовых ошибок. Следовательно, предел Хэмминга описанного кода (127,106) гарантирует исправление всех ошибок вплоть до 3-битовых.
Таблица 6.3. Предел возможностей коррекции для кода (127, 106)
Количество битовых ошибок Количество необходимых Общее число необходимых
классов смежности классов смежности
|
0 |
1 |
1 |
|
1 |
127 |
128 |
|
2 |
8001 |
8129 |
|
3 |
333375 |
341504 |
|
4 |
10334625 |
10676129 |
6.6.2. Пример кода (n, k)
Нормальная матрица дает возможность взглянуть на возможные компромиссы между исправлением и обнаружением ошибок. Рассмотрим пример кода (n, k) и факторы, определяющие выбор конкретных значений (n, k).
Для получения нетривиального соотношения между исправлением и обнаружением ошибок желательно, чтобы код имел возможности коррекции ошибок, по крайней мере, с t = 2. Согласно уравнению (6.44), минимальное расстояние при этом равно 
.
Чтобы кодовая система была нетривиальной, желательно, чтобы количество бит данных было не менее k = 2. Следовательно, число кодовых слов 
. Далее будем считать наш код следующим: (п, 2).
Нас интересует минимальное значение п, которое позволит исправлять все одно- и двухбитовые ошибки. В этом примере каждый из n-кортежей в матрице будет табулирован. Минимальное значение n нас интересует потому, что при каждом увеличении n на единицу число n-кортежей в нормальной матрице удваивается. Это условие, разумеется, диктуется только соображениями удобства использования таблицы. Для реальных прикладных кодов минимальное значение n выбирается по разнымпричинам—эффективность использования полосы пропускания и простота системы. Если при выборе n используется предел Хэмминга, то n следует выбрать равным 7. В то же время размерность полученного кода (7,2) не соответствует указанным выше требованиям t = 2 и 
. Чтобы увидеть это, следует ввести другую верхнюю границу возможностей кода в коррекции t-битовых ошибок (или 
) Эта граница, называемая предел Плоткина [7], определяется следующим образом.
(6.54)
Вообще, линейный код (n, k) должен удовлетворять всем перечисленным выше условиям, включая возможности коррекции ошибок (или минимальное расстояние). Для высокоскоростных кодов из удовлетворения предела Хэмминга следует удовлетворение предела Плоткина; это справедливо, например, для рассмотренного ранее кода (127,106). Для кодов с низкими скоростями передачи существует обходной путь удовлетворения названных требований [7]. Поскольку в нашем примере речь идет именно о таких кодах, важно оценить их возможности в коррекции ошибок с помощью предела Плоткина. Поскольку , из уравнения (6.53) получаем, что n должно быть равно 8; следовательно, для удовлетворения всех требований, поставленных в этом примере, минимальная размерность кода равна (8,2). Можно ли практически использовать подобный код (8,2)? Этого делать не стоит, поскольку это потребует слишком большой полосы пропускания; лучше выбрать более эффективный код. Данный код мы используем только с методической целью, единственным его преимуществом являются удобные размеры его нормальной матрицы.
6.6.3. Разработка кода (8, 2)
Ответ на вопрос, как выбираются кодовые слова из пространства 
8-кортежей, неоднозначен, хотя определенные ограничения выбора все же существуют. Ниже перечислены некоторые моменты, которые могут указать наилучшее решение.
1. Количество кодовых слов 
.
2. Среди кодовых слов должен быть нулевой вектор.
3 Следует учесть свойство замкнутости — сумма двух любых кодовых слов в пространстве должна давать кодовое слово из этого же пространства.
4. Каждое кодовое слово содержит 8 двоичных разрядов.
Поскольку , весовой коэффициент каждого кодового слова (за исключением нулевого) также должен быть не менее 5 (в силу свойства замкнутости). Весовой коэффициент вектора определяется как число ненулевых компонентов этого вектора.
5. Предположим, что код является систематическим; значит, 2 крайних правых бита каждого кодового слова являются соответствующими битами сообщения.
Далее предлагается вариант набора кодовых слов, удовлетворяющих всем перечисленным выше требованиям.
Сообщения Кодовые слова
|
00 |
00000000 |
|
01 |
11110001 |
|
10 |
00111110 |
|
11 |
11001111 |
Создание набора кодовых слов может выполняться совершенно произвольно; нужно только неуклонно следовать свойствам весовых коэффициентов и придерживаться систематической формы кода. Выбор первых нескольких кодовых слов обычно очень прост. Далее процесс, как правило, усложняется и возможность выбора все больше ограничивается за счет свойства замкнутости.
6.6.4. Соотношение между обнаружением и исправлением ошибок
Для кодовой системы (8,2), выбранной в предыдущем разделе, матрицу генератора 
можно записать в следующем виде.
Декодирование начинается с расчета синдрома, что можно представлять как изучение "симптомов" ошибки. Для кода (п, k) 
-битовый синдром S является произведением принятого n-битового вектора r и транспонированной проверочной матрицы Н размерностью 
. Проверочная матрица Н построена таким образом, что строки матрицы G ортогональны строкам матрицы Н, т.е.
. В нашем примере кода (8, 2) S — это 6-битовый вектор, а Н — матрица размером 6 х 8, где
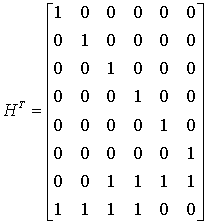
Синдром для каждой ошибочной комбинации можно рассчитать, исходя из уравнения (6.37), а именно
,
где 
— один из 
синдромов, а 
— один из 64 образующих элементов классов смежности (ошибочных комбинаций) в нормальной матрице. На рис. 6.15, помимо самой нормальной матрицы, показаны все 64 синдрома для кода (8, 2). Набор синдромов рассчитывался с помощью уравнения (6.37); позиции произвольной строки (смежный класс) нормальной матрицы имеют один и тот же синдром. Исправление искаженного кодового слова осуществляется путем расчета его синдрома и локализации ошибочной комбинации, соответствующей этому синдрому. В заключение ошибочная комбинация прибавляется (по модулю 2) к поврежденному кодовому слову, что и дает правильное кодовое слово. Из уравнения (6.49), повторно приведенного ниже, видно, что между возможностями обнаружения и исправления ошибок существует некий компромисс, ограничиваемый расстоянием.
Здесь 
представляет количество исправляемых битовых ошибок, а 
— количество обнаруживаемых битовых ошибок, причем 
. В коде (8,2) возможны следующие компромиссы между этими двумя величинами.
Обнаружение 
Исправление
|
2 |
2 |
|
3 |
1 |
|
4 |
0 |
Из данной таблицы видно, что код (8,2) можно использовать только для исправления ошибок; это означает, что код вначале обнаруживает 
ошибки, после чего они исправляются. Если пожертвовать возможностью исправления и использовать код для исправления только однобитовых ошибок, то возможность обнаружения ошибки возрастает до 
ошибок. И наконец, если целиком отказаться от исправления ошибок, то декодер сможет обнаруживать ошибки с 
. В случае, если ошибки только обнаруживаются, реализация декодера будет очень простой: производится вычисление синдрома и обнаруживается ошибка при появлении любого ненулевого синдрома.
Для исправления однобитовых ошибок декодер может реализовываться с логическими элементами [4], подобными приведенным на рис. 6.12, где принятый вектор кода 
поступал в схему в двух точках. В верхней части рисунка принятые символы поступают на логический элемент исключающего ИЛИ, который и определяет синдром. Для любого принятого вектора синдром рассчитывается согласно уравнению (6.35).
| 000000 | 1. | 00000000 | 11110001 | 00111110 | 11001111 |
| 111100 | 2. | 00000001 | 11110000 | 00111111 | 11001110 |
| 001111 | 3. | 00000010 | 11110011 | 00111100 | 11001101 |
| 000001 | 4. | 00000100 | 11110101 | 00111010 | 11001011 |
| 000010 | 5. | 00001000 | 11111001 | 00110110 | 11000111 |
| 000100 | 6. | 00010000 | 11100001 | 00101110 | 11011111 |
| 001000 | 7. | 00100000 | 11010001 | 00011110 | 11101111 |
| 010000 | 8. | 01000000 | 10110001 | 01111110 | 10001111 |
| 100000 | 9. | 10000000 | 01110001 | 10111110 | 01001111 |
| 110011 | 10. | 00000011 | 11110010 | 00111101 | 11001100 |
| 111101 | 11. | 00000101 | 11110100 | 00111011 | 11001010 |
| 111110 | 12. | 00001001 | 11111000 | 00110111 | 11000110 |
| 111000 | 13. | 00010001 | 11100000 | 00101111 | 11011110 |
| 110100 | 14. | 00100001 | 11010000 | 00011111 | 11101110 |
| 101100 | 15. | 01000001 | 01110000 | 01111111 | 10001110 |
| 011100 | 16. | 10000001 | 11110111 | 10111111 | 01001110 |
| 001110 | 17. | 00000110 | 11111011 | 00111000 | 11001001 |
| 001101 | 18. | 00001010 | 11111011 | 00110100 | 11000101 |
| 001011 | 19. | 00010010 | 11100011 | 00101100 | 11011101 |
| 000111 | 20. | 00100010 | 11010011 | 00011100 | 11101101 |
| 011111 | 21. | 01000010 | 10110011 | 01111100 | 10001101 |
| 101111 | 22. | 10000010 | 01110011 | 10111100 | 01001101 |
| 000011 | 23. | 00001100 | 11111101 | 00110010 | 11000011 |
| 000101 | 24. | 00010100 | 11100101 | 00101010 | 11011011 |
| 001001 | 25. | 00100100 | 11010101 | 00011010 | 11101011 |
| 010001 | 26. | 01000100 | 10110101 | 01111010 | 10001011 |
| 100001 | 27. | 10000100 | 01110101 | 10111010 | 01001011 |
| 000110 | 28. | 00011000 | 11101111 | 00001110 | 11010111 |
| 001010 | 29. | 00101000 | 11011001 | 00010110 | 11100111 |
| 010010 | 30. | 01001000 | 10111001 | 01110110 | 10000111 |
| 100010 | 31. | 10001000 | 01111001 | 10110110 | 01000111 |
| 001100 | 32. | 00110000 | 01000001 | 00001110 | 11111111 |
| 010100 | 33. | 01010000 | 10100001 | 01101110 | 10011111 |
| 100100 | 34. | 10010000 | 01100001 | 10101110 | 01011111 |
| 011000 | 35. | 01100000 | 10010001 | 01011110 | 10101111 |
| 101000 | 36. | 10100000 | 01010001 | 10011110 | 01101111 |
| 110000 | 37. | 11000000 | 00110001 | 11111110 | 00001111 |
| 110010 | 38. | 00000111 | 11100010 | 00111001 | 01101000 |
| 110111 | 39. | 00010011 | 11100010 | 00101101 | 11011100 |
| 111011 | 40. | 00100011 | 11010010 | 00011101 | 11101100 |
| 100011 | 41. | 01000011 | 10110010 | 01111101 | 10001100 |
| 010011 | 42. | 11000011 | 01110010 | 10111101 | 01001100 |
| 111111 | 43. | 10000011 | 11111100 | 00110011 | 11000010 |
| 111001 | 44. | 00010101 | 11100100 | 00101011 | 11011010 |
| 110101 | 45. | 00100101 | 11010100 | 00011011 | 11101010 |
| 101101 | 46. | 01000101 | 10110100 | 01111011 | 10001010 |
| 011101 | 47. | 10000101 | 01110100 | 10111011 | 01001010 |
| 011110 | 48. | 01000110 | 10110111 | 01111000 | 10001001 |
| 101110 | 49. | 10000110 | 01110111 | 10111000 | 01001001 |
| 100101 | 50. | 10010100 | 01100101 | 10101010 | 01011011 |
| 011001 | 51. | 01100100 | 10010101 | 01011010 | 10101011 |
| 110001 | 52. | 11000100 | 00110101 | 11111010 | 00001011 |
| 011010 | 53. | 01101000 | 10011001 | 01010110 | 10100111 |
| 010110 | 54. | 01011000 | 10101001 | 01100110 | 10010111 |
| 100110 | 55. | 10011000 | 01101001 | 10100110 | 01010111 |
| 101010 | 56. | 10101000 | 01011001 | 10010110 | 01100111 |
| 101001 | 57. | 10100100 | 01010101 | 10011010 | 01101011 |
| 100111 | 58. | 10100010 | 01010011 | 10011100 | 01101101 |
| 010111 | 59. | 01100010 | 10010011 | 01011100 | 10101101 |
| 010101 | 60. | 01010100 | 10100101 | 01101010 | 10011011 |
| 011011 | 61. | 01010010 | 10100011 | 01101100 | 10011101 |
| 110110 | 62. | 00101001 | 11011000 | 00010111 | 11100110 |
| 111010 | 63. | 00011001 | 11101000 | 00100111 | 11010110 |
| 101011 | 64. | 10010010 | 01100011 | 10101100 | 01011101 |
Рис. 6.15. Синдромы и нормальная матрица для кода(8, 2)
С помощью значений Нгдля кода (8,2), необходимо так соединить элементы схемы (подобно тому, как это было сделано на рис. 6.12), чтобы вычислялось следующее.
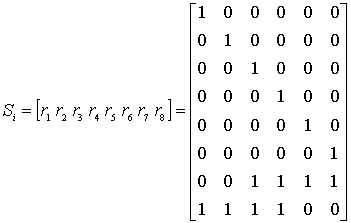
Каждая из цифр 
определяет синдром 
, связанный с входным принятым вектором кода следующим образом.
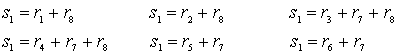
Для реализации схемы декодера для кода (8,2), подобной представленной на рис. 6.12, необходимо, чтобы восемь принятых разрядов соединялись с шестью сумматорами по модулю 2 (см. выше), выдающими цифры синдрома. Соответственно, потребуются и другие модификации схемы, приведенной на рисунке.
Если декодер реализован так, чтобы исправлять только однобитовые ошибки (т.е. 
), это эквивалентно ограничению матрицы на рис. 6.15 девятью первыми классами смежности, а исправление ошибок происходит, только когда один из восьми синдромов соответствует появлению однобитовой ошибки. Затем схема декодирования (подобная изображенной на рис. 6.12) преобразует синдром в соответствующую ошибочную комбинацию. Далее ошибочная комбинация прибавляется по модулю 2 к "потенциально" искаженному принятому вектору, т.е. происходит исправление ошибки. Для проверки ситуаций, когда синдром не равен нулю, а схемы коррекции нет, нужно вводить дополнительные логические элементы (например, для однобитовых ошибок, соответствующих синдромам 10-64).
Если декодер реализован так, чтобы исправлять одно- и двухбитовые ошибки (а это означает, что обнаруживается, а затем исправляется ошибки), это эквивалентно ограничению матрицы (рис. 6.15) 37 классом смежности. Хотя код (8,2) может исправлять некоторые комбинации трехбитовых ошибок, соответствующие образующим элементам классов смежности под номерами 38-64, декодер чаще всего реализуется как декодер с ограниченным расстоянием; это означает, что он исправляет все искаженные символы, содержащие ошибку только в t или меньшем числе бит. Нереализованные возможности используются для некоторого улучшения процесса обнаружения ошибок. Как и ранее, реализация декодера подобна схеме, изображенной на рис. 6.12.
6.6.5. Взгляд на код сквозь нормальную матрицу
В контексте рис. 6.15 код (8,2) удовлетворяет пределу Хэмминга. Иными словами, из нормальной матрицы можно видеть, что код (8,2) способен исправлять все комбинации одно- и двухбитовых ошибок. Рассмотрим следующее: пусть передача происходит по каналу, который всегда вносит ошибки в виде пакета 3-битовых ошибок, и, следовательно, нет необходимости в исправлении одно- или двухбитовых ошибок. Можно ли настроить образующие элементы классов смежности так, чтобы они соответствовали только трехбитовым ошибкам? Нетрудно определить, что в последовательности из 8 бит существует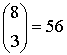 
возможностей произвести трехбитовую ошибку. Если единственным нашим желанием является коррекция только этих 56 комбинаций трехбитовых ошибок, то кажется, что в нормальной матрице достаточно места (достаточное количество классов смежности), поскольку всего в ней имеется 64 строки. Будет ли это работать? Однозначно, нет. Для любого кода главным параметром, определяющим способности кода к коррекции ошибок, является . Для кода (8, 2) , а это означает, что возможно исправление только 2-битовых ошибок.
Как стандартная матрица может помочь разобраться, почему эта схема не будет работать? Чтобы осуществить исправление x-битовых ошибок для группы x-битовых ошибочных комбинаций, полная группа векторов с весовым коэффициентом х должна быть классом смежности, т.е. они должны находиться только в крайнем левом столбце. На рис. 6.15 можно видеть, что все векторы с весовым коэффициентом 1 и 2 находятся в крайнем левом столбце нормальной матрицы и нигде более. Если мы даже и втиснем все векторы с весовым коэффициентом 3 в строку со второго номера по 57-й, увидим, что некоторые из этих векторов снова появятся в матрице где-нибудь еще (что нарушит основное свойство нормальной матрицы). На рис. 6.15 затененные блоки обозначают те 56 векторов, которые имеют весовой коэффициент 3. Взгляните на образующие элементы классов смежности, представляющие 3-битовые ошибочные комбинации, в строках 38, 41-43, 46-49 и 52 нормальной матрицы. Потом посмотрите на позиций в тех же строках в крайнем правом столбце, где затененные блоки показывают другие векторы с весовым коэффициентом 3. Видите некоторую неопределенность, существующую для каждой строки, о которых говорилось выше, и понятно ли теперь, почему нельзя исправить все 3-битовые ошибочные комбинации с помощью кода (8,2)? Допустим, декодер принял вектор с весовым коэффициентом 3 — 11001000, размещенный в строке 38 в крайнем правом столбце. Это искаженное кодовое слово могло появиться, во-первых, при передаче кодового слова 1 1 0 0 1 1 1 1, искаженного 3-битовой ошибочной комбинацией 0 0 0 0 0 1 1 1, а во-вторых, при передаче кодового слова 00000000, искаженного 3-битовой ошибочной комбинацией 1 1 0 0 1 0 0 0.