Функция фильтрации. В общем виде электрические фильтры описываются передаточной функцией вида: 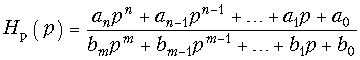(17.1)

Квадрат амплитудно-частотной характеристики таких фильтров 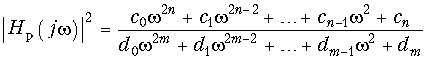(17.2) и, следовательно, рабочее ослабление 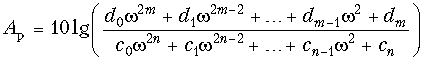(17.3) могут при надлежащем выборе степени полинома (порядка фильтра) и коэффициентов d_k удовлетворить заданным требования (см. рис. 17.3).

В теории фильтров принято иметь дело не с обычной угловой частотой , а с нормированной частотой , где – нормирующая частота. Обычно в качестве нормирующей частоты выбирают граничную частоту полосы пропускания , так что .

В теории электрических фильтров вместо формул (17.2) и (17.3) используют другие, также универсальные для любого типа фильтра: 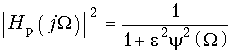(17.4) (17.5)

Функция называется функцией фильтрации, а – коэффициентом неравномерности ослабления. В общем случае – это дробно-рациональная функция с вещественными коэффициентами (в частности полином), удовлетворяющая условиям: –1 1 в полосе пропускания и >> 1 в полосе непропускания фильтра.

В зависимости от вида функции фильтрации получают различные типы фильтров. Если в качестве функции фильтрации используют полиномы, то фильтры называются полиномиальными. Среди полиномиальных фильтров широкое использование нашли фильтры Баттерворта и Чебышева. Если – дробно-рациональная функция, например, дробь Золотарева, то получают фильтр Золотарева. Все эти три типа фильтров будут рассмотрены в этой главе.

Следует отметить, что имеет смысл подробно изучать только фильтры нижних частот, т. к. другие типы фильтров (верхних частот, полосовые и заграждающие) могут быть легко получены из ФНЧ с помощью замены переменной (частоты). Для этого во всех выражениях, содержащих переменную , нужно произвести замену переменной таким образом, чтобы характеристики ФНЧ А_р() и |H_р(j)|² преобразовались в характеристики соответствующего фильтра. Подобная замена переменной называется преобразованием частоты, а исходный ФНЧ – фильтром НЧ-прототипа.

Преобразование частоты позволяет установить соответствие между частотами полос пропускания и непропускания НЧ-прототипа и частотами фильтров верхних частот, полосового или заграждающего, а также преобразовать схему ФНЧ в схемы ФВЧ, ПФ или ЗФ. Более подробно вопросы, связанные с преобразованием частоты, будут рассматриваться в 17.5. Резонаторные фильтры.

Фильтры Баттерворта. Если в выражениях, описывающих квадрат АЧХ фильтра (17.4) и его рабочее ослабление (17.5), в качестве функции фильтрации используются полиномы Баттерворта = B_m() = ^m (по имени автора, предложившего использовать их для "конструирования" частотных характеристик фильтра), то такие фильтры называются фильтрами Баттерворта.

Из формул (17.4) и (17.5) следует, что для фильтров Баттерворта на частоте = 0 значение квадрата АЧХ равно единице, а рабочего ослабления – нулю. С ростом частоты квадрат АЧХ фильтра Баттерворта уменьшается и падает до нуля на бесконечно большой частоте. Рабочее ослабление плавно растет до бесконечно большого значения. Таким образом, выражения (17.4) и (17.5) приближенно воспроизводят характеристики идеального фильтра.

Чтобы эти характеристики "вписывались" в предъявляемые к фильтру требования (см. рис. 17.3), необходимо иметь рабочее ослабление (17.5) в полосе пропускания меньшее А_рmax, а в полосе непропускания большее А_рmin. Первому условию можно удовлетворить, если потребовать на граничной частоте полосы пропускания ( = 1) выполнения равенства А_р()₌₁ = А_рmax или |H_р(j)| = . Отсюда с учетом (17.5) или (17.4) имеем 1 + ² = и ² = – 1. Вычисленный таким способом коэффициент : (17.6) называется коэффициентом неравномерности ослабления в полосе пропускания фильтра.

В формуле (17.6) величина А_рmax имеет размерность непер. Если воспользоваться значениями А_рmax в децибелах, то (17.7)

С учетом введенных обозначений квадрат АЧХ фильтра Баттерворта запишется в виде (17.8)

Эта функция удовлетворяет свойствам квадрата АЧХ реальных четырехполюсников, и поэтому ей можно сопоставить физически осуществимый электрический фильтр.

Рабочее ослабление фильтра Баттерворта: (17.9)

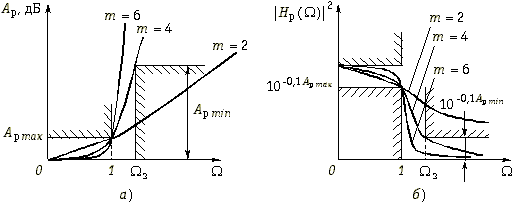
Рис. 17.4

Крутизна частотных характеристик (17.8) и (17.9) зависит от степени m (порядка фильтра). Чем больше степень m, тем выше крутизна характеристик. На рис. 17.4, а, и б показаны графики рабочего ослабления и квадрата АЧХ фильтра Баттерворта для различных m. Таким образом, для удовлетворения требований в полосе непропускания необходимо выбрать соответствующий порядок фильтра m. Его легко определить из условия: на граничной частоте полосы непропускания: _з А_р(_з) А_рmin или |H_р (j)| . С учетом этого условия получим 1 + ² > , откуда . Логарифмируя обе части неравенства, придем к выражению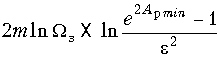

Из него находим окончательно

m (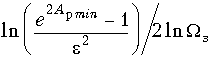17.10)

Величина А_рmin входит в формулу в неперах. Если вычислять ее в децибелах, то: m (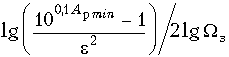17.11)

Передаточную функцию фильтра Баттерворта можно получить из (17.8), если положить j = p: 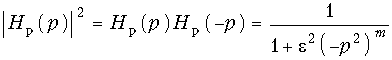(17.12) и разложить знаменатель полученной функции на произведение сомножителей.

Вычислим корни знаменателя, т. е. полюсы функции H_р(p) X H_р(–p), отдельно для четных и нечетных значений m. Для четных значений m: и 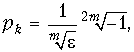k = 1, 2, ..., 2m.

Так как: , имеем: 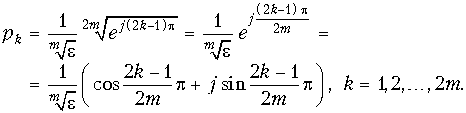(17.13)

Для нечетных значений m: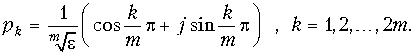

Выражение (17.12) примет вид: .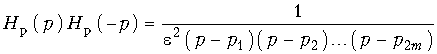

Половина полюсов функции H_р(p)H_р(–p) лежит в левой полуплоскости комплексной переменной p и может быть отнесена к передаточной функции реализуемого фильтра H_р(p). Другая половина полюсов, являясь зеркальным отражением первой, располагается в правой полуплоскости и относится к H_р(–p).

Построенная из полюсов, лежащих в левой полуплоскости, передаточная функция фильтра Баттерворта является полиномиальной передаточной функцией типа (17.1): , где H = 1/.

Пример. Найти выражения для частотной характеристики и передаточной функции фильтра нижних частот Баттерворта, удовлетворяющего следующим требованиям: А_рmax = 3 дБ; А_рmin = 12,2 дБ; f_п = 159 кГц; f_з = 318 кГц.

Определим нормированную частоту _з = f_з/f_n = 2 и по формуле (17.7) коэффициент неравномерности ослабления ² = 10^0,1×3 – 1 = 1. Порядок фильтра найдем согласно (17.11): .

Выберем m = 2. Тогда в соответствии с (17.8) и (17.9): .

Найдем передаточную функцию фильтра H_р(p). Значения полюсов функции |H_р(p)|² = H_р(p)H_р(–p) = 1/ (1 + р⁴) вычислим из формулы (17.13): p₁ = 0,707 + j0,707; p₂ = – 0,707 + j0,707; p₃ = – 0,707 – j0,707; p₄ = 0,707 – j0,707. Расположение полюсов в комплексной плоскости показано на рис. 17.5, а.

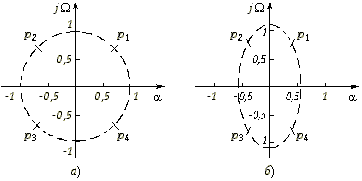
Рис. 17.5

По теореме Виета из полюсов в левой полуплоскости p₂ и p₃ формируем передаточную функцию: .

Используя введенное ранее обозначение B_m() = ^m полинома Баттерворта, можно представить частотные характеристики (17.8) и (17.9) фильтра Баттерворта в следующей форме: 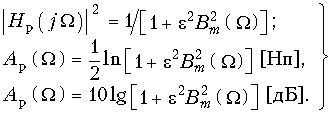(17.14)

Фильтры Баттерворта называют также фильтрами с максимально плоским ослаблением в полосе пропускания (см. рис. 17.4, а).

Полиномиальные фильтры Чебышева. Если в качестве функции фильтрации в (17.4) и (17.5) использовать полином Чебышева, обозначаемый ( ) = T_m( ), то формулы (17.14) примут вид: 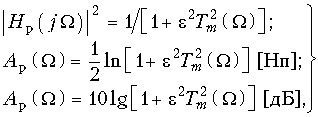(17.15) где T_m() – полином Чебышева степени (порядка) m; – коэффициент неравномерности, определяемый (17.6) или (17.7).

Фильтры с частотными характеристиками (17.15) называются фильтрами Чебышева. Проанализируем частотные характеристики фильтра Чебышева. Для этого вначале рассмотрим свойства полиномов T_m(). Ниже приведены шесть первых полиномов Чебышева: 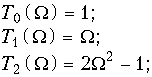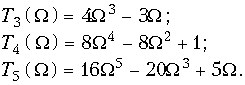(17.16 а)

Любой полином Чебышева при m 2 может быть вычислен по рекуррентной формуле T_m( ) = 2 T_m–1( ) – T_m–2( ). Таким образом, выражения (17.15) удовлетворяют общим выражениям (17.1) – (17.3) характеристик полиномиальных фильтров.

Существует единая тригонометрическая форма записи полиномов Чебышева в интервале –1 1:

(17.16)

Действительно, T₀( ) = cos0arccos = 1; T₁( ) = cos1arccos = = ; T₂( ) = cos2arccos = 2cos²arccos – 1 = 2 ² – 1. Вне интервала –1 1 полиномы T_m( ) также представляются в тригонометрической форме:

(17.16 в)

Анализ поведения полиномов Чебышева показывает, что в интервале –1 1 угол = arccos изменяется от – (при = –1) до 0 (при = 1), поэтому полином T_m() = cosm ровно m раз принимает значения, равные нулю, и m + 1 раз достигает значений, равных +1 или –1 и чередующихся друг с другом. Вне интервала –1 1 полином T_m( ) согласно формуле (17.16 в) монотонно возрастает. В качестве примера на рис. 17.6, а изображен график полинома Чебышева T₄(), т. е. полинома четвертого порядка.

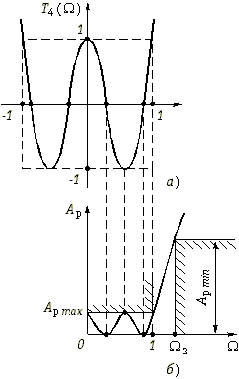
Рис. 17.6

В соответствии с (17.15) рабочее ослабление A_p() фильтра Чебышева на тех частотах , где полином T_m() обращается в нуль, также обращается в нуль. На частотах, на которых T_m() равен 1, рабочее ослабление достигает величины: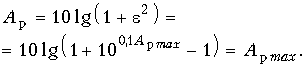

С ростом значений полинома T_m() на частотах > 1 рабочее ослабление A_p() также монотонно растет. На рис. 17.6, б приведен график рабочего ослабления фильтра Чебышева четвертого порядка.

Фильтры Чебышева называют также фильтрами с равноволновой характеристикой ослабления в полосе пропускания.

На рис. 17.7 показаны частотные зависимости квадрата АЧХ фильтра Чебышева для различных значений m, полученные для |H_р(j)|² из (17.15). Подобные зависимости могут быть построены для рабочего ослабления фильтра.

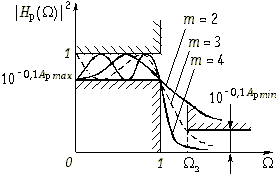
Рис. 17.7

Чтобы характеристики фильтра отвечали требованиям в полосе непропускания, необходимо выбрать порядок фильтра m из условия |H_р(j)| . Для полосы непропускания T_m( ) определяется формулой (17.16 в), следовательно, 1 + ²сh²m X Arch_з . Отсюда сhmArch_з . Далее mArch _з и m .

В этой формуле величина A_pmin измеряется в неперах. При использовании единицы децибел порядок фильтра вычисляется из выражения:

m (17.17 a)

Сравнивая частотные характеристики фильтров Баттерворта и Чебышева, следует указать, что полиномы Чебышева являются полиномами наилучшего приближения. Это означает, что при одинаковом значении m из всех полиномиальных фильтров, ослабления которых в полосе пропускания не превышают A_pmax, наибольшие значения ослабления в полосе непропускания имеет фильтр Чебышева. В частности, рабочее ослабление фильтра Чебышева в полосе непропускания может превышать (и весьма значительно) рабочее ослабление фильтра Баттерворта при равных значениях m и A_pmax. Однако характеристика рабочего ослабления фильтра Баттерворта имеет в полосе пропускания монотонный характер и легче поддается корректированию для устранения искажений передаваемых сигналов.

Выбор типа полиномиальных фильтров определяется конкретными условиями их применения в аппаратуре связи и радиотехнических устройствах.

Для получения передаточной функции фильтра Чебышева поступим аналогично тому, как делали это для фильтров Баттерворта. Заменим оператор j на оператор р и перейдем от функции |H_р(j )|² к функции: .

Представим полином T_m() в виде (17.16 б) и найдем полюсы функции |H_р(p)|², решив уравнение: (17.17 б)

Поскольку согласно (17.16 а) коэффициент при старшем члене полинома Чебышева T_m( ) равен 2^m–1, то коэффициент при старшем члене полинома в левой части приведенного выше уравнения равен ²2^2(m–1).

Корни уравнения (17.17 б), как можно доказать, определяются аналитически следующим выражением: (17.18) где .

Из корней в левой полуплоскости составляются сомножители (p - p_i), и по теореме Виета строится передаточная функция фильтра: , где .

Пример. Построить передаточную функцию фильтра Чебышева второго порядка (m = 2), рабочее ослабление в полосе пропускания (от 0 до 159 кГц) которого не превышает величину A_pmax = 3 дБ. Граничная частота полосы непропускания 318 кГц.

Коэффициент неравномерности такого фильтра согласно (17.7) равен 1. Рабочее ослабление на частоте _з = 318/159 = 2 составляет A_p( )₌₂ = 10lg(1 + ch²2Arch2) = 17 дБ, что почти на 5 дБ превышает рабочее ослабление на этой же частоте фильтра Баттерворта второго порядка (см. предыдущий пример).

Расчет полюсов функции H_p(p)H_p(–p) по формулам (17.18) дает величины: p₁ = 0,322 + j0,777; p₂ = 0,322 – j0,777; p₃ = –0,322 – j0,777; p₄ = –0,322 + j0,777. Расположение полюсов в комплексной плоскости показано на рис. 17.5, б.

Передаточная функция фильтра: .

В заключение отметим, что для полиномиальных фильтров в справочниках составлены весьма полные таблицы полюсов и коэффициентов передаточных функций для различных величин A_pmax и m. Порядок же фильтров m определяется по специальным графикам, исходя из заданных величин A_pmax, A_pmin и _з.

Фильтры со всплесками ослабления (на основе дробей Чебышева и Золотарева). Частотные характеристики полиномиальных фильтров, описываемые выражениями (17.1)—(17.3), имеют монотонный характер в полосе непропускания. В частности, рабочее ослабление таких фильтров монотонно возрастает по мере удаления от полосы пропускания (рис. 17.4, а и 17.6, б).

При "жестких" требованиях к частотным характеристикам (малая переходная область между полосами пропускания и непропускания и большая величина рабочего ослабления в полосе непропускания) порядок фильтра m может получиться очень большим даже в случае применения полинома Чебышева. Это приведет к существенному усложнению фильтра и к излишнему "расходу" элементов.

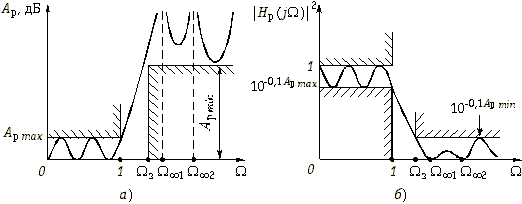
Рис. 17.8

В таких случаях целесообразно применять фильтры со всплесками рабочего ослабления в полосе непропускания (рис. 17.8, а). На частотах всплеска ₁, ₂ и т. д. рабочее ослабление фильтра стремится к бесконечности; за счет этого возрастает крутизна характеристики ослабления в переходной области. Соответственно АЧХ фильтра на частотах ₁, ₂ и т. д. будет обращаться в нуль (рис. 17.8, б).

Для выполнения указанных условий в выражениях (17.2)—(17.3) используют рациональные дроби вида: 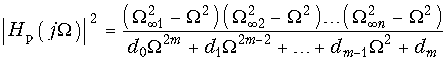(17.19) 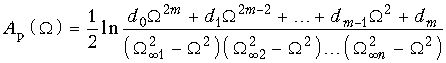(17.20)

Действительно, когда принимает значения ₁, ₂, ..., _n, |H_р(j )|² = 0 и A_р() .

Передаточная функция таких фильтров является дробно-рациональной: 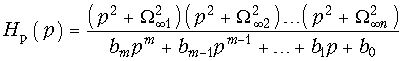(17.21) и кроме полюсов p₁, p₂, ..., p_m имеет нули: .

Фильтры со всплесками рабочего ослабления называют еще фильтрами с нулями передачи.

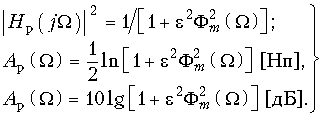Среди фильтров со всплесками ослабления наиболее широкое распространение получили фильтры, построенные на основе дробей Чебышева и Золотарева. Чтобы получить частотные характеристики фильтра на основе дробей Чебышева, нужно в формулах (17.14) или (17.15) использовать в качестве функции фильтрации дробь Чебышева. Обозначая ее Ф_m( ), получим: (17.22)

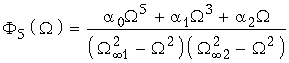В качестве примера укажем дробь Чебышева пятого порядка, для которой построены графики A_р() и |H_р(j)|² на рис. 17.8, а и б: , где a₀, a₁ и a₂ – коэффициенты, связанные с частотами всплеска ₁ и ₂.

Очевидно, что подстановка этой дроби в (17.22) приведет после некоторых преобразований к выражениям общего вида (17.19) и (17.20).

В полосе пропускания дробь Чебышева ведет себя так же, как и полином Чебышева, т. е. рабочее ослабление фильтра носит равноволновый характер. На частотах всплеска ₁ и ₂ дробь Чебышева обращается в бесконечность, что приводит к бесконечно большому рабочему ослаблению.

Следует отметить, что дробь Чебышева является дробью наилучшего приближения. Это означает, что фильтр на основе дроби Чебышева на любой частоте полосы непропускания имеет большее значение рабочего ослабления по сравнению с фильтрами на основе других дробей (и полиномов, как частных случаев дробей) при прочих равных условиях (при одинаковых порядках m, при таком же количестве и расположении частот всплеска и тех же величинах A_pmax).

Частным случаем дробей Чебышева являются дроби Золотарева: (17.23) где , , значение S равно 0 для четных m и равно 1 для нечетных m; m – порядок дроби; _0V, _V – нули и полюсы дроби, связанные соотношением _V = _{з/ 0V}.

Используя в качестве функции фильтрации в (17.14) и (17.15) дроби Золотарева, получим: 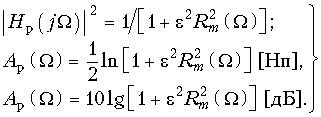(17.24)

Из формул (17.23) и (17.24) следует, что нули функции A_р( ) совпадают с нулями дроби Золотарева, а всплески функции A_р( ) – с полюсами этой же дроби. Нули и полюсы дроби Золотарева можно рассчитывать, однако обычно их определяют по каталогам для операторных передаточных функций ФНЧ. На рис. 17.9 показан график A_р( ) для фильтра Золотарева пятого порядка.

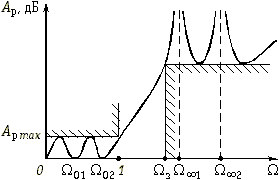
Рис. 17.9

Дроби Золотарева так же, как и полиномы Чебышева, дают равноволновую характеристику рабочего ослабления фильтра в полосе пропускания. Однако в полосе непропускания у фильтров Золотарева значения всех минимумов рабочего ослабления оказываются одинаковыми и равными значению рабочего ослабления на частоте _з. Такие фильтры называются также фильтрами с изоэкстремальными характеристиками рабочего ослабления.

Фильтры с характеристиками Золотарева можно рассматривать как частный случай фильтров с характеристиками Чебышева, когда значения минимумов ослабления фильтра в полосе непропускания выравнены, а число всплесков – максимально возможное при выбранном значении m.