1. Основной физической идеей квантовой теории является идея о том, что корпускулярно-волновая двойственность свойств характерна не только для фотонов, частиц электромагнитного поля, но и для всех частиц вещества: электронов, протонов, нейтронов, атомов, молекул и т.д.

В 1924 году де Бройль писал: "Каждое движущееся тело сопровождается волной, и разделение движения тела и распространения волны является невозможным". Идея де Бройля о волновых свойствах частиц вещества блестяще подтвердилась экспериментально.

Длина волны де Бройля задаётся формулой:

,

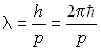где h и - постоянные Планка, р - импульс частицы (тела).

2. При решении задач необходимо учитывать, является ли частица релятивистской или классической. Импульс частицы:

а) в классическом (нерелятивистском) случае:

б) в релятивистском случае:

,

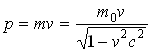где m₀ - масса покоя, с - скорость света в вакууме.

3. Критерий того, является ли движущаяся частица (тело) релятивистской, или нет, задаётся соотношением:

если , или - частица классическая, , соответственно кинетическая энергия и энергия покоя, если , или - частица релятивистская.

4. Импульс частицы связан с кинетической энергией:

а) в нерелятивистском случае:

;

б) в релятивистском случае:

,

где - энергия покоя.

5. Если заряженная частица с зарядом q ускоряется в электрическом поле, пройдя разность потенциалов U, то волна де Бройля такой частицы задаётся соотношением:

а) в классическом случае:

;

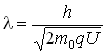б) в релятивистском случае:

.

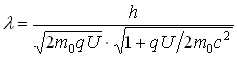6. Характеристиками волны являются её групповая и фазовая скорости. Эти понятия можно использовать и для волн де Бройля.

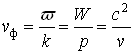
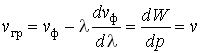
где ω, λ - частота и длина волны де Бройля, W, P, v - энергия, импульс и скорость частицы, - волновое число.

7. Пользуясь основным соотношением между энергией и импульсом частицы, фазовую скорость можно выразить следующим образом:

,

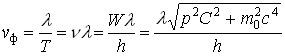что говорит о дисперсии волн де Бройля (явление дисперсии характерно для волновых процессов).

8. Экспериментальным подтверждением существования волн де Бройля являются результаты опытов по дифракции движущихся частиц (в том числе, атомов, молекул). Для объяснения дифракционной картины используется формула Вульфа - Брэггов:

,

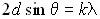где k = 1,2,3,... - порядок спектра, d - межплоскостное расстояние (постоянная кристаллической решётки), θ - угол скольжения (угол между направлением движения частицы и поверхностью кристалла).