Задача оптимальной фильтрации непрерывного сигнала ставится следующим образом: требуется так обработать принятый сигнал x(t)=s(t)+ (t), чтобы получить на выходе приемника сигнал y(t), наименее отличающийся от переданного сигнала s(t). Математическое решение этой задачи было дано А. Н. Колмогоровым и Н. Винером. Теория Колмогорова—Винера базируется на трех основных предположениях: 1) сигнал s(t) и помеха (t) представляют собой стационарные случайные процессы; 2) операция фильтрации предполагается линейной; 3) критерием оптимальности считается минимум среднеквадратической ошибки.

Пусть сигнал s(t) и шум (t) являются независимыми случайными процессами с известными корреляционными функциями Bs(t) и Bw(), a x(t) — сигнал на входе линейного фильтра с импульсной характеристикой g(t). Требуется найти такую функцию g(t), чтобы сигнал на выходе фильтра y(t) минимизировал среднеквадратическую ошибку

Требование физической реализуемости фильтра, как известно, сводится к тому, что импульсная реакция фильтра должна удовлетворять условию g(t)=0 для всех t<0. Это ограничение учитывается в записи

где область интегрирования для физически реализуемого фильтра есть интервал от 0 до , а для нереализуемого фильтра — от до

Докажем вначале, что характеристика фильтра g(t) оптимальна тогда и только тогда, когда

для из (4.54)

т. е. когда ошибка (t)=y(t)—s(t) некоррелирована со входным сигналом x(t) во все моменты времени в области

Пусть — импульсная характеристика оптимального фильтра, для которого справедливо условие (4.54), а для — импульсная характеристика любого другого линейного фильтра. Отклики фильтров соответственно обозначим через y(t) и y(t) Тогда

Так как функция и (t) удовлетворяет (4.54), то

Следовательно,

Очевидно это выражение будет минимальным, когда что и доказывает справедливость условия (4.54).

Представим соотношение (4.54) в виде отсюда получаем

или

(4.55)

В случае, когда сигнал s(t) и помеха w(i) независимы, ур-ние (4.55) принимает вид

(4.56)

Это интегральное уравнение является основным уравнением теории линейной фильтрации и называется уравнением Винера — Хопфа. Его решением является искомая функция g(t), минимизирующая среднеквадратическую ошибку ².

Уравнение (4.56) решается сравнительно просто, если , т. е. для нереализуемых фильтров. Для реализуемых фильтров задача существенно усложняется. Ниже приводится упрощенная теория линейной фильтрации [12, 13].

Квадрат среднеквадратической ошибки может быть выражен через энергетический спектр ошибки:

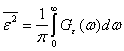(4.57)

где— энергетический спектр функции (t)=y(t)—s(t—t) ,t0 — время задержки сигнала.

Определим сначала функцию корреляции ошибки

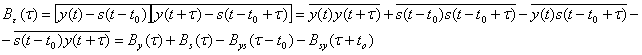
(4.58)

Так как преобразование Фурье, связывающее между собой B() и

G() линейно, то для спектра ошибки имеем

(4.59)

Выражение для Gу() находим непосредственно по ф-ле (2.109):

Так как s(t) и (t) независимы, то и Остается найти взаимные спектральные плотности Gsy и Gys. Согласно (2.8,1) имеем

(4.60)

Но отклик фильтра y(t) выражается интегралом Дюамеля

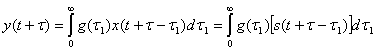(4.61)

После подстановки (4.61) в выражение (4.60), учитывая, что и импульсная реакция фильтра g(t) связана с коэффициентом передачи К(i) парой, преобразований Фурье, получим

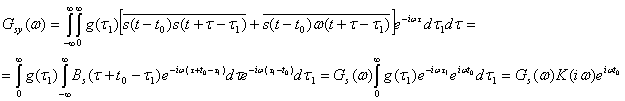
Так как К(i) =, тo

Энергетический спектр есть действительная величина, поэтому мнимый показатель экспоненты должен быть равен нулю, т. е.

(4.62)

Выражение (4.62) определяет фазовую характеристику оптимального фильтра. Итак,

Аналогично определяется Легко показать, что

Окончательно выражение (4.59) для спектра погрешности принимает вид

Теперь нужно найти такое значение К(), при котором среднеквадратическая погрешность ² (4.57) будет наименьшей. Для этого достаточно минимизировать G. Перепишем выражение для в виде

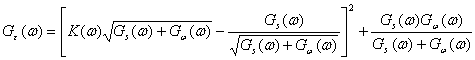
Первый член положителен и зависит от К(), второй член — заданная величина. Ясно, что наименьшее значение будет иметь тогда, когда выражение в квадратных скобках будет равно нулю. При этом условии

или с учетом (4.62)

(4.63).

При этом спектр ошибки

(4.64).

а средний квадрат ошибки равен:

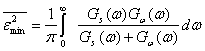(4.65).

Заметим, что сигнал может быть полностью отделен от помехи, т.е. ошибка будет равна нулю лишь при условии . Последнее означает, что спектры сигнала и помехи не перекрываются (рис. 4.12а). Если помеха отсутствует, то ,, =1 т. е. фильтра не требуется.

Фильтр с оптимальной характеристикой (4.63) пропускает колебание различных частот с тем меньшим весом, чем больше отношение при данной частоте. Например, если спектры сигнала и помехи перекрываются, как показано на рис. 4.126, то частотная характеристика фильтра должна иметь вид, показанный на том же рисунке пунктиром. Если отношение сигнала к помехе мало: то 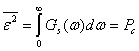т. е. погрешность очень велика и восстановление сигнала при помощи фильтрации становится невозможным.

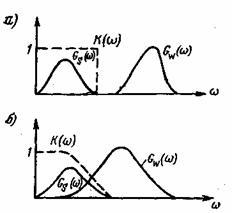
Рис. 4.12. Частотная характеристика оптимального фильтра: спектры сигнала и помехи не перекрываются (а), спектры сигнала и помехи перекрываются (б).

Можно получить лучший результат при фильтрации, если применить так называемое предыскажение. Передача с предыскажением состоит в том, что и на передающей стороне сигнал s(t) пропускается через фильтр с коэффициентом передачи. Полученный таким образом видоизмененный сигнал передается по каналу. На приемной стороне ставится другой фильтр С коэффициентом передачи К- Характеристики фильтров Ки К выбираются так, чтобы обеспечить минимум среднеквадратической ошибки. Расчеты показывают [12], что предыскажение дает тем больший выигрыш, чем меньше относительная ширина полосы перекрытия спектров сигнала и помехи