Если луч света падает на границу раздела двух фаз (рис.1.4а), то часть света отражается под углом, равным углу падения, а часть света уходит во вторую фазу под углом j_o, величина которого определяется уравнением Снеллиуса:

(1.1),

где n_c и n_o – показатели преломления (ПП) материалов сердцевины и оболочки соответственно. Если n_c > n_o, то j_o > j_c и при увеличении угла падения может наступить момент при j_c = j_k, когда луч не выходит во вторую фазу, а распространяется по границе фаз (рис.1.4 б). При большем угле падения света будет происходить только отражение (рис. 1.4 в). Таким образом, явление полного внутреннего отражения имеет место, когда угол падения больше критического угла равного

(1.2)

ОВ работает на принципе полного внутреннего отражения поскольку ПП материала сердцевины всегда больше ПП материала оболочки.

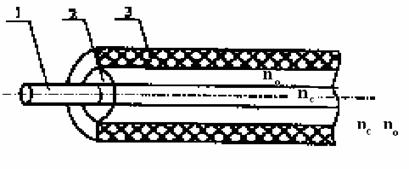
Рис. 1.5. Структура оптического волокна: 1 – сердцевина, 2 – светоотражающая оболочка, 3 – защитно-упрочняющее покрытие

На рис.1.5 приведена структура ОВ, которое состоит из сердцевины (1), светоотражающей оболочки (2) и защитно-упрочняющего покрытия (3). Ход лучей в ОВ со ступенчатым профилем ПП от источника света, распо-ложенного на оси волокна, показан на рис. 1.6. Надо сказать, что профиль

ПП (т.е. радиальное распределение ПП в сечении ОВ) имеет большое значение для распространения света по ОВ. Ступенчатый ПП является простейшим вариантом.

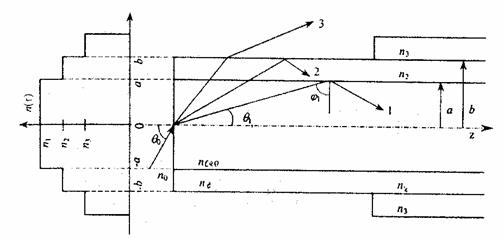
Рис.1.6. Модель ОВ со ступенчатым профилем показателя преломления

На рис. 1.6 видно, что луч 1, испытывающий полное внутренне отражение, будет распространять по ОВ. Луч 2 выходит в светоотражающую оболочку и, если оптические потери материала этой оболочки велико, то он будет затухать, а если малы, то он может распространяться в этой оболочке (что имеет место в одномодовых ОВ). Луч 3 выходит не только из сердцевины, но и из светоотражающей оболочки и будет затухать либо в окружающей среде, либо в защитной оболочке. Лучи, распространяющиеся по ОВ, называются направляемыми модами, а те лучи, которые выходят наружу, - вытекающими модами или модами излучения. Различают также меридиональные лучи, которые пересекают ось ОВ, и косые лучи, которые не пересекают эту ось (рис.1.7).

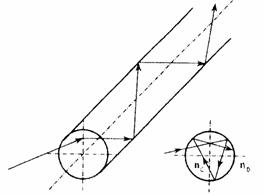
Рис. 1.7. Траектория прохождения косого луча в ОВ.

Одной из важнейших характеристик ОВ является его числовая апертура, которая обозначается как NA и вычисляется по уравнению:

(1.3).

Таким образом, числовая апертура представляет собой телесный угол, в пределах которого находятся лучи, которые могут распространяться по ОВ (рис. 1.8).

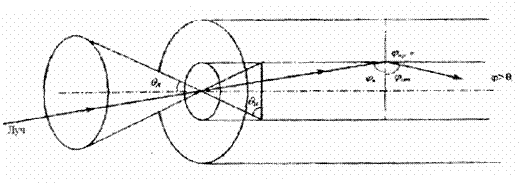
Рис. 1.8. Принцип действия ОВ