В качестве переносчика можно использовать не только периодические колебания, но и узкополосный случайный процесс. Такие переносчики также находят практическое применение. Например, в оптических системах связи, в которых используется некогерентное излучение, сигнал, по существу, представляет собой узкополосный гауссов шум.

Согласно (2.36) узкополосный случайный процесс можно представить как квазигармоническое колебание

с медленно изменяющимися огибающей и фазой . При амплитудной модуляции в соответствии с передаваемым сообщением изменяется огибающая U(t), при фазовой модуляции — фаза и при частотной — мгновенная частота .

Рассмотрим амплитудную модуляцию шумовой несущей. Выражение для модулированной несущей в этом случае можно записать в виде

y(t) = [1 + ти(t)]f(t), (3.57)

где f(t) — переносчик, u(t) — модулирующая функция (видеосигнал), m — коэффициент модуляции.

Предполагается, что модулирующий процесс u(t) также представляет собой стационарный нормальный процесс со средним значением, равным нулю u(t) = 0. Процессы f(t) и u(t) независимы. При этих ограничениях функция корреляции модулированной по амплитуде шумовой несущей будет

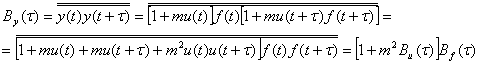(3.58)

Теперь находим энергетический спектр

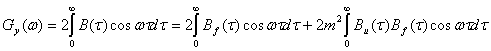
Первый интеграл дает энергетический спектр шумовой несущей . Для второго интеграла на основании теоремы о спектре произведения имеем

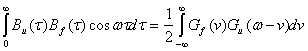
Окончательно спектр модулированной несущей будет равен:

(3.59)

Таким образом, спектр модулированной по амплитуде шумовой несущей получается суперпозицией спектра несущей и свертки этого спектра со спектром передаваемого сообщения, сдвинутого в область высоких частот на величину .Аналогично определяются функция корреляции и энергетический спектр при ФМ и ЧМ.

Применение «шумовых» сигналов позволяет ослабить влияние замираний в каналах с многолучевым распространением радиоволн. Поясним это на простейшем примере. Пусть на вход приемника поступают сигналы двух лучей и сдвигом на τ. время т. Мощность результирующего сигнала, определяемая за достаточно большое время Т,

где — функция корреляции сигнала, Р0— его средняя мощность. Функция корреляции шума быстро убывает с увеличением т и тем быстрее, чем шире его спектр. Следовательно, при достаточно большой ширине спектра можно считать 0 и , т. е. средняя мощность принятого сигнала, несмотря на замирания, остается примерно постоянной.