8.1. Профиль показателя преломления в заготовках ОВ
8.2. Геометрические размеры ОВ
После получения заготовок и вытяжки ОВ измеряют их основные оптические параметры, которые вносят в паспорт на ОВ. Здесь рассмотрим лишь те методы измерения этих параметров, которые используют для контроля за качеством ОВ на этапе их изготовления. К таким параметрам относятся:
профиль ПП в заготовках ОВ;
геометрические размеры в ОВ;
коэффициент затухания;
числовая апертура ОВ;
диаметр модового пятна в одномодовых ОВ;
длина волны отсечки в одномодовых ОВ;
хроматическая дисперсия в одномодовых ОВ или ширина пллосы пропускания в многомодовых ОВ.
8.1. Профиль ПП в заготовках ОВ
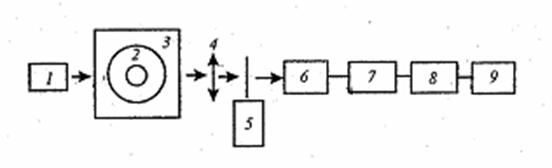
Рис. 8.1. Структурная схема анализатора заготовок: 1 – He-Ne лазер, 2 – заготовка ОВ, 3 – ячейка с иммерсионной жидкостью, 4 – линза, 5 – модулятор, 6 – сканирующий фотоприемник, 7 – устройство обработки, 8 – персональный компьютер, 9 - графопостроитель
Для измерения профиля ПП в заготовке ОВ используется метод отклонения луча при поперечном сканировании заготовки. На рис. 8.1 приведена схема установки, называемой обычно преформ-анализатором (анализатором заготовки). Заготовка помещается в кювету с иммерсионной жидкостью, ПП которой близок ПП материала заготовки. Луч света, проходя через заготовку, преломляется в ней. С помощью сканирующего фотоприемника измеряется угол преломленного луча для многих положений луча. Данные вводятся в персональный компьютер, который на основании проведенных измерений рассчитывает зависимость n(r). В данном сечении измерения проводят в двух взаимно перпендикулярных направлениях, что позволяет контролировать эллиптичность сердцевины и оболочки. Для примера на рис. 8.2 приведены профили ПП в заготовках радиационно-стойкого одномодового ОВ с кварцевой сердцевиной и фторсиликатной "депрессированной" светоотражающей оболочкой, полученной при использовании в качестве фторагента SiF4 (1) либо при использовании в качестве фторагента сначала SF6, а затем SiF4. Считается, что профиль ПП в ОВ тождественен измеренному профилю ПП в заготовке, хотя он может иногда и заметно отличаться.
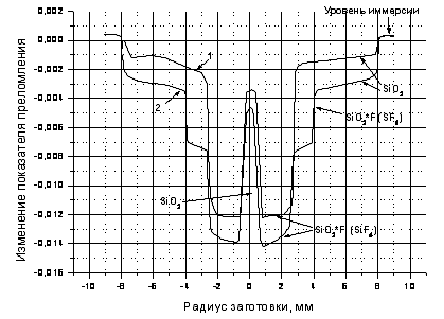
Рис. 8.2. Профильи ПП в заготовках радиационно-стойких ОВ с кварцевой сердцевиной и депрессированной фторсиликатной оболочкой: 1 – фторагент – SiF4, 2- фторагенты – первоначально SF6, а затем SiF4
8.2. Геометрические размеры ОВ
Геометрические размеры в ОВ измеряются с помощью микроскопа (обычно специализированного –"Fiber-check"), обеспечивающего точность измерения десятые доли мкм. К измеряемым геометрическим параметрам относятся: диаметр кварцевого волокна, диаметр волокна с защитным покрытием, неконцентричность сердцевины и волокна, некруглость волокна, диаметр модового пятна и т. д. В таблице 5.2 приведены типичные значения этих параметров для стандартных одномодовых ОВ (типа SM-28).
8.3. Измерение потерь
Существуют три метода измерения потерь (коэффициента затухания) в ОВ: метод "облома", метод обратного рассеяния и измерение потерь с помощью оптических тестеров (мультиметров).
1. Метод облома наиболее широко используется для измерения спектральной зависимости полных потерь в ОВ. Схема метода показана на рис. 8.3.
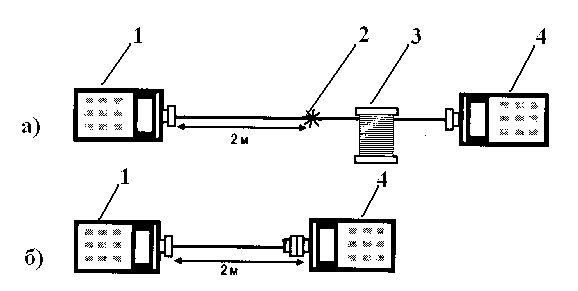
Рис. 8.3. Схема измерения потерь в волокне методом «облома»: 1 – источник света с монохроматором, 2 – место облома, 3 – тестируемое волокно, 4 - фотоприемник
Свет через монохроматор на определенной длине волны (1) вводится в ОВ (3) и затем попадает на фотоприемник (4). Сначала (рис. 8.3а) снимают спектральное пропускание света большим отрезком волокна (Lдл.), затем, не трогая систему ввода света в волокно, обламывают его, оставляя отрезок длиной 2-5 м (Lкор.), и измеряют спектральное пропускание короткого отрез-
ка ОВ (рис. 8.3б). Величину потерь для каждой длины волны определяют по формуле:
![]() дБ/км (8.1),
дБ/км (8.1),
где Ркор. и Рдл. – интенсивности света на выходе из короткого и длинного кусков волокна соответственно. Спектральную зависимость потерь часто строят в масштабе a=f(l-4), что дает возможность определить коэффициент Рэлеев
ского рассеяния (А) и величину "серых" потерь (В). Для примера на рис. 8.4 приведена подобная спектральная зависимость полных потерь в одном из образцов одномодового ОВ с германосиликатной сердцевиной. В данном случае А = 1,39 дБ/км*мкм 4 и В=0,23 дБ/км. Пик в области 1…1,15 мкм обусловлен отсечкой высшей моды, а пики на l = 1,25 и 1,38 мкм – гидроксильными группами.
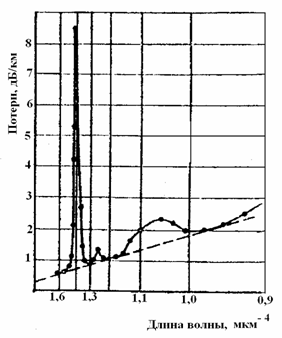
Рис. 8.4. Спектральная зависимость полных потерь в образце ОВ с германосиликатной сердцевиной, построенная в координатах α=f (λ-4)
2. Метод обратного рассеяния применяется для измерения потерь на определенной длине волны (обычно 1,3 или 1,55 мкм) с помощью рефлектометра. Принцип работы рефлектометра (OTDR – Optical Time Domain Reflectometer) следующий: в ОВ посылают мощный оптический импульс, который рассеиваясь на неоднородностях (в том числе рэлеевских), возвращается назад и с помощью ответвителя поступает на фотоприемник. Измеряя мощность и время запаздывания импульсов, вернувшихся обратно в рефлектометр, можно определить величину погонных потерь и потери на отдельных "дефектных" участках (например, в местах сварки волокон). На рис. 8.5 приведена блок-схема рефлектометра, а на рис. 8.6 показана типичная рефлектограмма, по которой можно вычислить как погонные потери в ОВ, так и величину отдельных дефектов.
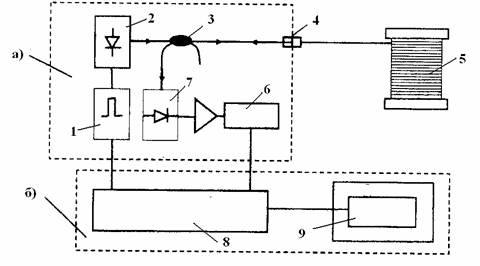
Рис. 8.5. Блок- схема рефлектометра: а) – оптический модуль, б) - базовый модуль: 1 – импульсный генератор, 2 - лазерный диод, 3 – ответвитель, 4 – оптический разъем, 5 – оптическое волокно, 6 – АЦП, 7 – фотоприемник, 8 – микропроцессоры RISC и Intel, 9 - дисплей
Величина потерь вычисляется в этом случае по формуле:
a(z) = 5 lg (P0/Pz) – 5 lg(S0/Sz) (7.2),
где P0 и Pz – мощности импульса в начале и в конце волокна длиной (z), S0 и Sz – коэффициенты рассеяния в начале и в конце волокна. Коэффициент перед логарифмами равен 5, а не 10 (как в уравнении 1.4) поскольку импульс проходит двойное расстояние: от начала к концу и затем возвращается назад к началу волокна.
Если коэффициент рассеяния постоянен вдоль всего волокна (линии), т.е. Sz=S0, то второе слагаемое обращается в ноль, и показания рефлектометра будут прямо пропорциональны величине потерь в волокне (линии). Вариации коэффициента рассеяния возникают, в основном, из-за вариаций диаметра модового пятна, что приводит к появлению систематической погрешности, пропорциональной величине изменения диаметра модового пятна (Dw/w). Эту систематическую погрешность можно устранить, если измерить рефлектограммы с обеих сторон волокна (линии), тогда полусумма рефлектограмм будет показывать изменение коэффициента рассеяния, а полуразность рефлектограмм – изменение величины потерь.
Следует отметить, что рефлектометры используются не только для измерения потерь в волокнах, оптических кабелях и линиях связи, но и для измерения расстояний до неоднородностей волокне (дефектов сварки, трещины в волокне и т.д.), которые после обнаружения можно устранять.
Погрешность измерений возникает за счет:
- инструментальных ошибок, связанных с неточность измерения начала и конца волокна, с ошибками в калибровке горизонтальной шкалы;
- методических ошибок, возникающих из-за того, что неоднородности на рефлектограмме получаются разными для отражающей и неотражающей неоднородности;
- ошибок оператора и т.д.
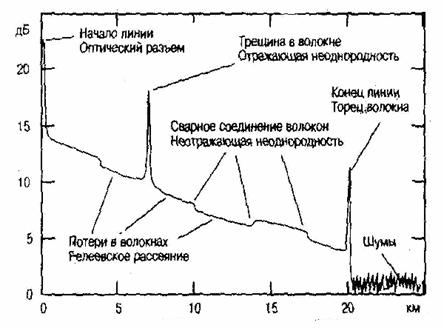
Рис. 8.6. Типичная рефлектограмма линии передачи. По вертикальной оси в логарифмическом масштабе откладывается мощность вернувшихся в рефлектометр импульсов, а по горизонтальной оси – расстояние до места отражения
3. Схема измерения потерь в волокне с помощью мультиметров (оптических тесторов) показана на рис. 8.7. В начале оператор, соединив вход и выход мультиметра оптическим шнуром, измеряет величину опорного сигнала. Затем он отсоединяет разъем шнура от розетки фотоприемного блока и подсоединяет через розетку к началу волокна (линии), а выходной конец волокна подсоединяет к фотоприемному блоку второго мультиметра. Величина потерь (с учетом разности показаний фотоприемных блоков, полученных в процессе их сверки) рассчитывается по формуле:
a (дБ) = опорный сигнал в дБм – сигнал в дБм (8.3),
где дБм – мощность оптического излучения (Р), соотнесенная с 1 мВт, т.е.
a = 10 lg (P/1 мВт) (8.4).
Измерение потерь с помощью мультиметров проводится на конкретных длинах волн (обычно 0,85; 1,3 или 1,55 мкм).
При такой системе измерений погрешность возникает в основном по следующим причинам:
· нестабильность источника излучения,
· нелинейность шкалы мультиметра,
· разная чувствительность фотоприемных блоков на разных концах волокна (линии),
· отклонение величины потерь в разъемах от их номинального значения.
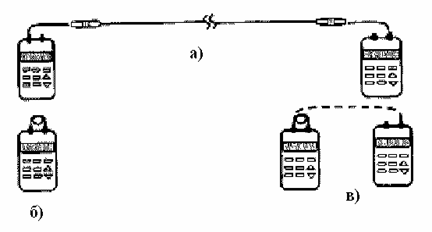
Рис. 8.7. Измерение потерь с помощью мультиметров: а) – измерение мощности излучения, прошедшего через линию, б) – измерение опорного сигнала, в) – сверка фотоприемных блоков
8.4. Числовая апертура
Числовая апертура измеряется методом дальнего поля, т.е. по изображению излучения, выходящего из волокна, на экране. Измеряя диаметр светового пятна на экране и расстояние от торца волокна до экрана, величину числовой апертуры можно вычислить по формуле:
NA = (nc2 – no2)1/2 =n0 Sinq » 2 tg (d/2l) = dп/l (8.5),
где nc и n0 – показатели преломления сердцевины и оболочки соответ-ственно, q - телесный угол, в пределах которого лучи распространяются по волокну без вытекания, dп – диаметр светового пятна на экран, l – расстояние от торца волокна до экрана.
8.5. Модовое пятно
Диаметр модового пятна (w) является одной из важнейших характеристик одномодовых ОВ, поскольку определяет согласование волокон между собой, величины изгибных и микроизгибных потерь и т.д. Диаметр модового пятна отличается от диаметра сердцевины в ОВ, причем это отличие увеличивается с уменьшением величины нормализованной частоты, и для одномодовых световодов со ступенчатым профилем ПП записывается согласно формуле (5,6). На рис. 8.8 приведена спектральная зависимость диаметра модового пятна для одного из образцов ОВ. Видно, что с ростом длины волны (соответственно, с уменьшением V) диаметр модового пятна также растет, а наименьшее его значение находится вблизи длины волны отсечки высшей моды (λс). Существует несколько методов измерения диаметра модового пятна, остановимся на 2-х из них, рекомендованных Международным стандартом.
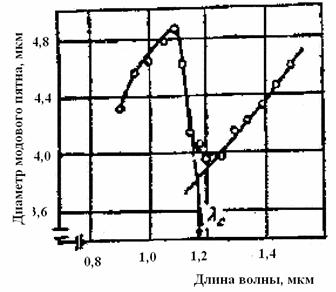
Рис. 8.8. Спектральная зависимость диаметра модового пятна
Метод поперечного сдвига заключается в том, что свет вводят в два состыкованных между собой волокна, а затем торец второго волокна начинают перемещать относительно выходного торца первого волокна, (т.е. его сканировать), снимая при этом показания интенсивности света на выходе второго волокна. Диаметр модового пятна определяют по уровню 1/е2»0,135 радиального распределения интенсивности света, как это видно на рис. 8.9. Второй метод, принятый американским бюро стандартов TIA, основан на диафрагмировании картины дальнего поля таким образом, чтобы интегральная интенсивность света в диафрагмированной области составляла 1-0,135 = 0,865 от общей интенсивности света на картине дальнего поля. Диаметр модового пятна рассчитывают используя отношение диаметров отверстий диафрагмы, позволяющей получать оба эти случая.
8.6. Длина волны отсечки
Условие одномодового излучения в ОВ получается из следующего соотношения рабочей длины волны (l) с длиной волны отсечки (lс) LP11-моды: l>lс. Значение lс определяется критическим значением нормализованной частоты (Vc£ 2,405), а, следовательно, видом профиля ПП волокна. Теоретически строго рассчитать величину lс можно только для ОВ со ступенчатым профилем ПП, поэтому эффективную длину волны отсечки для одномдового ОВ с любым профилем ПП обычно определяют экспериментально. В предыдущем разделе было показано, что величину lс можно определить методом поперечного сдвига. Однако более распространен метод изгиба, который основан на сравнении спектральных зависимостей пропускания света в одномодовых ОВ с изгибом – Р(l) и без него – Р0(l). При измерениях принято брать образец волокна длиной ~ 2 м и изгиб делать радиусом около 20 мм. За величину lс в методе изгиба принимают длину волны, на которой имеет ме сто увеличение относительного пропускания Р0-Р на 0,1 дБ по сравнению с плоским участком (рис. 8.10).
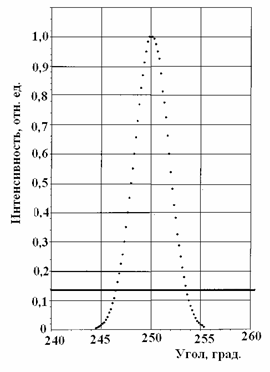
Рис. 8.9. Угловое распределение интенсивности света, выходящего из волокна («дальнее поле»)
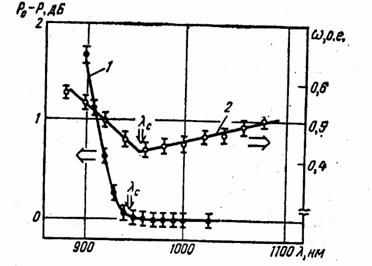
Рис. 8.10. Спектральные зависимости: 1 – разности пропускания света прямым и изогнутым волокном, 2 – диаметра модового пятна
8.7. Межмодовая дисперсия
Межмодовая дисперсия присуща многомодовому волокну и обусловлена тем, что все моды распространяются по различным траекториям. Это приводит к тому, что огибающие модулированного светового сигнала различных мод по мере распространения сигнала все больше и больше отличаются по фазе. Межмодовая дисперсия обычно ограничивает расстояние передачи по многомодовому ОВ до 1÷1,5 км , обеспечивая битовую скорость до 1 Гб/с. При измерениях межмодовая дисперсия обычно определяется наименьшим значением частоты, при которой амплитудно-частотная характеристика спадает на 3 дБ (т.е. в 2 раза). В общем случае измерение межмодовой дисперсии сводится к измерению полосы частот многомодового волокна на различных длинах волн. Схема измерения межмодовой дисперсии многомодового волокна импульсным методом приведена на рис. 8.11.
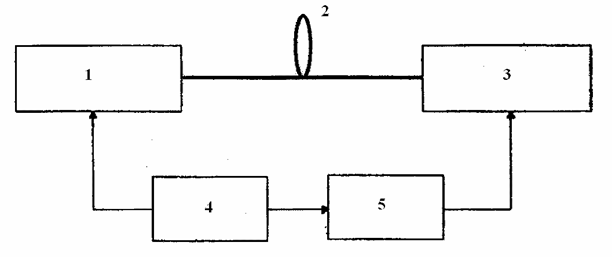
Рис. 8.11. Схема измерения межмодовой дисперсии многомодового волокна импульсным методом: 1 – источник излучения (светодиод), 2- измеряемое волокно, 3 – стробоскопический осциллограф, 4- регулятор задержки, 5 – генератор импульсов
В процессе измерения в тестируемом волокне возбуждается импульс излучения заданной длительности, а выходной импульс преобразуется в цифровую форму, включая передний и задний фронт и начиная с 0,01 уровня амплитудного значения. Затем таким же образом измеряется входной импульс, здесь используется короткий кусок (в несколько метров) тестируемого или эталонного волокна. Функция преобразования тестируемого волокна в этом случае имеет вид
H(f) = B(f) / A(f) (8.6),
где B(f) и A(f) – преобразования Фурье входного и выходного импульсов, соответственно. Полоса частот волокна определяется как самая низкая частота, для которой |H(f)|=0,5. Для повторяемости результатов и возбуждения большого количества мод на входе устанавливается устройство скремблирования.
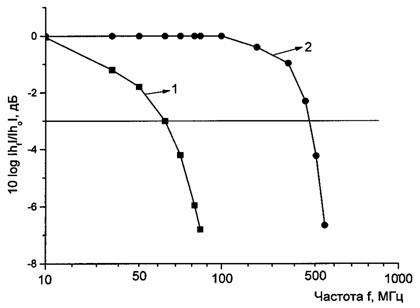
Рис. 8.12. Амплитудно-частотные характеристики оптических волокон: 1 - ступенчатый профиль показателя преломления, 2 – градиентный профиль показателя преломления
Для примера на рис. 8.12 приведены амплитудно-частотные характеристики ОВ со ступенчатым (1) и градиентным (2) профилями показателя преломления. Видно, что в первом случае полоса пропускания по уровню -3 дБ (0,5 высоты амплитуды) составляет ~ 65 МГц, а во втором ~ 500 МГц.
8.8. Хроматическая дисперсия
Хроматическая дисперсия вместе с величиной потерь определяет длину ретрансляционного участка в ВОСПИ, использующих одномодовые ОВ. Прямое определение хроматической дисперсии в одномодовых ОВ посредством измерения уширения прошедшего через ОВ импульса возможно лишь при использовании отрезков ОВ длиной несколько километров и требует пикосекундных излучателей и приемников. На практике применяются методы, в которых вначале определяется спектральная зависимость временной задержки t(l) при прохождении излучения через отрезок ОВ длиной L, а хроматическую дисперсию находят из выражения
![]() (8.7).
(8.7).
При измерении t(l) в качестве источника часто используется волоконный ВКР-лазер (рамановский) с широким световым континуумом. В зависимости от l измеряется изменение времени задержки между импульсом, запускающим лазер, и импульсом, поступающим с фотоприемника. На рис. 8.13 приведена схема установки.
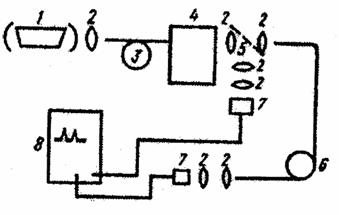
Рис. 8.13 Схема установки для измерения хроматической дисперсии: 1 – Nd-ИАГ-лазер, 2 – объективы, 3 – ВКР-лазер, 4 - монохроматор ,5 – полупрозрачное зеркало, 6 – волокно, 7 – германиевый лавинный фотодиод, 8 – осциллограф
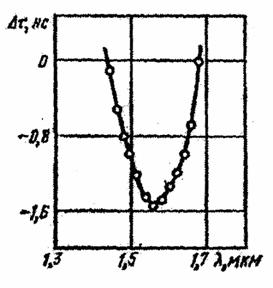
Рис.8.14. Спектральная зависимость величины хроматической дисперсии для ОВ со смещенной дисперсией
Для формирования оптических потоков и фокусировки применяется светоделительная пластина (5) и линзы (2). На рис. 8.14 приведены экспериментальные результаты, полученные для одномодового ОВ (L~1 км) со смещенной дисперсией. Подобный метод удобен для лабораторных исследований, т.к. он прост в реализации и вследствие большого набора спектральных точек допускает точную аппроксимацию.
Часто используют другую форму записи данных t(l) через ДВНД (l0), соответствующее ей значение t0=t(l0) и наклон дисперсионной кривой S0 в точке l0 S0=dC(l)/dlIl=l0. При этом существуют различные формы записи аппроксимирующих выражений:
t = t0 + (S-0/8)´(l - l02/l)2 (8.8),
t = t0 + (S0/2)´(l - l0)2 – (S0/6)´(l - l0)3 (8.9)
и т.д.
Если требуется провести измерение дисперсии на коротких отрезках ОВ, обычно применяют интерференционный метод, основанный на использовании интерферометра Маха-Цендера (рис. 8.15), в одно из плеч которого помещается короткий (~ 1м) отрезок ОВ, а длина оптического пути во втором, воздушном плече может изменяться при помощи задержки таким образом, чтобы сравняться с оптическим путем в ОВ в исследуемом диапазоне длин волн.
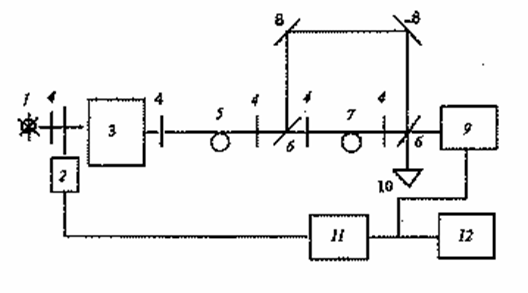
Рис. 8. 15. Схема интерференционного метода измерения хроматической дисперсии ОВ: 1 – галогенная лампе, 2 – модулятор, 3 – монохроматор, 4 – микрообъективы, 5 – возбуждающее ОВ, полупрозрачное зеркало, 7 – исследуемое ОВ, 8 – зеркало со 100 % отражением, 9 – фотоприемник, 10 – призма на пьезокерамической подвижке, 11 – усилитель, 12 - самописец
Изменяя длину линии задержки (изменение положения призмы 10 с помощью микрометрической подачи), можно добиться совпадения оптических путей в воздухе и исследуемом ОВ. Возникший при этом интерференционный сигнал регистрируется фотоприемником. В эксперименте измеряется зависимость величины интерференционного сигнала от длины линии задержки для фиксированной длины волны l. На основании этих данных строится зависимость относительной линии задержки Dl, соответствующей максимуму интерференционного сигнала, от l. Эта зависимость пересчитывается в спектральную зависимость временной задержки
Dt (l) = Dl(l)/с (8.10),
где с – скорость света в вакууме. Величина хроматической дисперсии рассчитывается по формуле (8.10).

