8.1. Методы определения потребностей

8.1.1. Метод экспертных оценок

8.1.2. Экстраполяционные методы

8.1.3. Нормативные методы

8.1.4. Сравнительный метод

8.1. Методы определения потребностей

Потребности – исторически сложившиеся запросы людей в услугах связи, развивающиеся с развитием средств связи.

Спрос – форма проявления потребностей с учетом возможности потребителя в оплате услуг связи.

Пример: заявки на установку телефонов. Потребление услуг связи – это удовлетворенный спрос потребителей на услуги связи с учетом возможностей предприятий связи и покупательной способности населения.

8.1.1. Метод экспертных оценок

Метод экспертных оценок (МЭО) используется при планировании в условиях неопределенности. МЭО предполагает нахождение управляющего решения на основе знаний, интуиции, логики какой-либо проблемы с количественной оценкой результатов и формализованной обработкой результатов. Полученное в результате обработки обобщенное мнение экспертов принимается как основное направление решения проблемы.

В связи область применения, например:

• при выборе технических средств;

• при выборе руководителей различного уровня;

• в различных ситуациях, когда недостаточно объема информации.

Этапы МЭО.

I этап. Подбор экспертов. Эффективность решения проблемы методом экспертных оценок определяется характеристиками достоверности экспертизы, которая зависит от общего числа экспертов в группе, долевого состава различных специалистов и характеристик экспертов.

Для описания экспертов с точки зрения качества решения проблемы используются следующие характеристики:

1. компетентность – степень квалификации в данной проблеме
   К = 0.5(К_и + К_а), (8.1)где К_и – коэффициент информированности;
   К_а – коэффициент аргументации;
2. креативность – способность творчески мыслить, создавать;
3. конформизм – подверженность влиянию авторитетов других (неустойчивое мнение);
4. самокритичность;
5. отношение к экспертизе – должно быть положительным;
6. достоверность оценки
   Д_i = N_пр/N, (8.2)где N_пр – количество правильных результатов по предыдущим экспертизам;
   N – общее количество экспертов.

Количественные характеристики, от которых зависит эффективность решения проблемы можно отразить на графике (рис. 8.1)

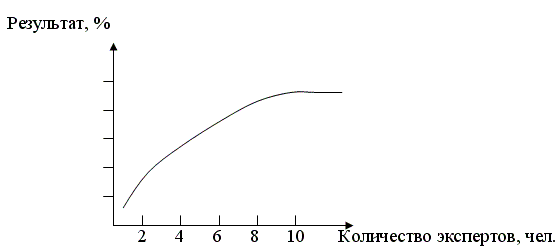
Рисунок 8.1. Количественные характеристики, от которых зависит эффективность решения проблемы

II этап. Выбор способа обработки информации, получаемой от экспертов.

Экспертное оценивание представляет собой процесс измерения, который можно представить как процедуру сравнения объектов по выбранным показателям или критериям.

Способы измерения:

1. 1. Ранжирование – упорядочение объектов, которое выполняет эксперт. При ранжировании эксперт должен расставить объекты в порядке предпочтения относительно одного или нескольких критериев, причем самому предпочтительному объекту присваивается число натурального ряда 1, менее предпочтительному – 2 и т.д. Если эксперт присваивает разным объектам одинаковый ранг, то необходимо рассчитать стандартизированный ранг S

   

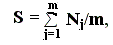
   где N_j – ранг j-го объекта с одинаковым значением ранга;
   Σ - сумма мест объектов с одинаковым рангом;
   m – число объектов с одинаковым рангом.

   Таблица 8.1. Пример расчета стандартизированного ранга
   

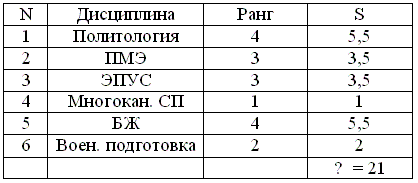
   S_2,3 = (3+4)/2 = 3,5
   S_1,5 = (5+6)/2 = 5,5

   Σ = n(n+1)/2, (8.4)где Σ - сумма стандартизированных рангов;
   n – количество объектов (факторов).

   Ранжирование используется чаще всего, когда число сравниваемых объектов ≤ 20.

2. Непосредственная оценка. При этом способе объектам присваиваются числовые значения в шкале интервалов, т.е. эксперту предлагается поставить в соответствие каждому объекту точку на непрерывной оси, например, [0, 1]. С целью упрощения этой процедуры при непосредственной оценке вместо непрерывной оси используют балльную шкалу: 5-ти балльную, 10-ти балльную, 100 балльную и т.д. Менее предпочтительному объекту присваивается наименьший балл, затем по возрастанию.
3. Последовательное сравнение. При последовательном сравнении процедура (сравнения) измерения состоит из ранжирования и из непосредственной оценки.
4. Парное сравнение. Представляет собой процедуру установления предпочтения при сравнении всех возможных пар объектов.

После проставления оценок осуществляется их обработка. В зависимости от цели экспертного оценивания и выбранного способа измерений при обработке экспертных оценок могут решаться следующие задачи:

1. Построение обобщенной оценки объектов на основе индивидуальных оценок экспертов

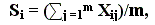   ^(8.5)

   где Σ_j=1^m X_ij – оценка, данная i-му объекту j-ым экспертом;
   m – количество экспертов.

2. Определение величины относительных весов объектов.
3. Определение согласованности мнений экспертов. Для оценки согласованности используется коэффициент конкордации W

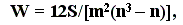   ^(8.6)

   где m – количество экспертов;
   n – количество объектов;
   S – обобщенная оценка.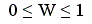

   

   Чем ближе W к 1, тем выше согласованность экспертов.

При наличии связанных рангов

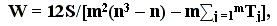^(8.7)

где T_j – показатель связанных рангов.

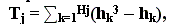^(8.8)

где H_j – число групп равных рангов в j-ой ранжировке; h_k – число равных рангов в k-ой ранжировке j-ым экспертом.

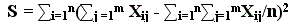^(8.9)

Таблица 8.2 – Исходные данные для расчета показателя связанных рангов

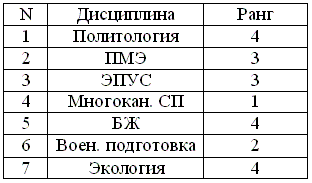
T_j = (2³ – 2) + (3³ – 3) = 6 + 24 = 30 2 – количество ранга 3
3 – количество ранга 4

8.1.2. Экстраполяционные методы.

Статистические методы планирования основаны на сборе статистики прошлых лет, выявлении закономерностей и их экстраполяции на перспективу.

Корреляционный метод.

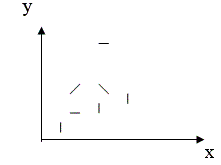
Рисунок 8.2. Корреляционное поле

Сущность метода: при планировании междугородных разговоров (функция) путем логического анализа определяется фактор (х) – количество телефонных аппаратов. В отчетном периоде собирается статистика, т.е. отчетные данные, на основании которых наносятся точки корреляционного поля. По расположению точек корреляционного поля устанавливается наличие зависимости функции от фактора y = f(x) и характер зависимости – прямая линия, парабола, гипербола и т.д. Устанавливается коэффициент тесноты связи между фактором и функцией (коэффициент корреляции). Если коэффициент >0,7 и ближе к 1, то связь считается достаточно сильной и полученное уравнение может быть использовано для планирования междугородных разговоров. Таким образом, строится модель задачи, т.е. уравнение связи между фактором и функцией.

Пример. Если расположение точек корреляционного поля ближе к прямой, то рассчитываются параметры уравнения y = a + xb. Для определения a и b используется система нормальных уравнений

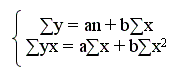
Система нормальных уравнений решается относительно a и b. Таким образом, получается уравнение, которое описывает зависимость y = f(x), она экстраполируется далее.

Определяется коэффициент корреляции r

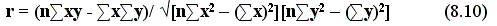
Чаще всего на функцию влияет множество факторов, тогда функция y зависит от множества х. y = f(x₁, x₂, …, x_n) r, η, R, 0,7
R – коэффициент множественной корреляции, оценивает точность расчета
η – коэффициент тесноты связи для непрямолинейных зависимостей

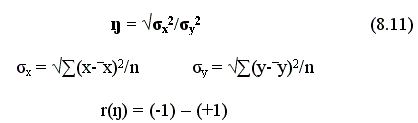
Метод вычисления тренда.

Метод вычисления тренда – это корреляционная зависимость, где в качестве фактора используется время и косвенно через фактор времени действует все множество факторов.

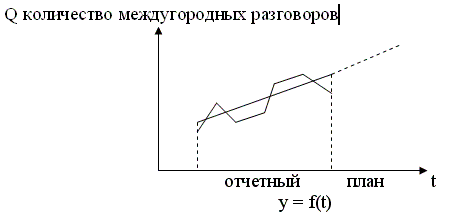
Рисунок 8.3. Метод вычисления тренда

Особенность статистических методов: их можно использовать, если сохраняется характер действия факторов, не происходит серьезных изменений. Если наблюдаются серьезные изменения, то статистические методы использовать нельзя, тогда используются нормативные методы.

8.1.3. Нормативные методы

Низкие темпы развития отрасли на перспективу планировать нельзя, если необходимо произвести взрывоподобное развитие отрасли. В этом случае используются нормативные методы.

N_та = n_{тел. плотн.}*Ч_насел, (8.12)

где n – нормативное количество телефонных аппаратов на 100 жителей

Телефонная плотность – это показатель, который признан одним из 14 важнейших показателей, характеризующих уровень развития экономики страны.

8.1.4. Сравнительный метод

Сравнительный метод носит вспомогательное значение, как ориентир для оценки уровней развития других стран и в своей стране.