При переходе от преобразования Фурье к z-преобразованию была сделана замена
.
Для перехода от передаточной функции 
к частотной характеристике 
необходимо произвести обратную замену
.
Обычно вводят в рассмотрение нормированную частоту W = f × T = 
. С учетом этого формула (24) примет вид:
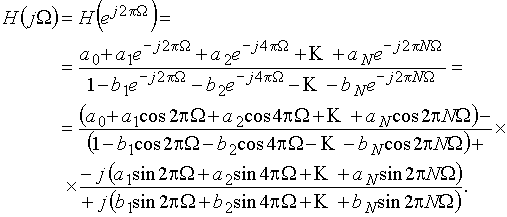(26)
Из (26) легко получить амплитудно-частотную и фазо-частотную характеристики дискретной цепи. В частности, амплитудно-частотная характеристика будет представлена выражением
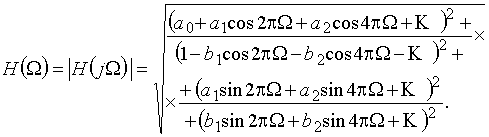(27)
Пример 17.1. Рассмотрим цифровой фильтр Баттерворта нижних частот, приведенный на рис. 49,б и описываемый передаточной функцией (25). Подстановка в (25) 
дает
.
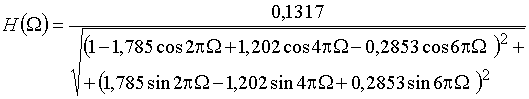На рис. 50 изображен график АЧХ 
этого фильтра. Как и следовало ожидать, амплитудно-частотная характеристика дискретной цепи является периодической функцией (так как 
есть преобразование Фурье от дискретной импульсной реакции). Ее период равен 
или 
. Поэтому она используется в диапазоне частот от 0 до 
(или до W = 0,5).
Пример 17.2. Найдем частотную характеристику цифрового фильтра с импульсной характеристикой 
= {1,5; 1; 0,5}.
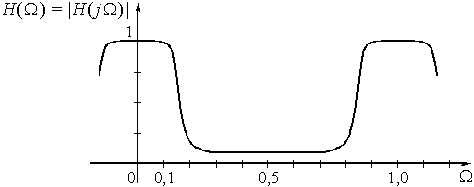
Рис. 50
Запишем передаточную функцию 
цифрового фильтра, воспользовавшись формулой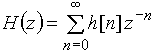 
. Получим 
передаточную функцию нерекурсивного фильтра.
Найдем АЧХ этого фильтра, подставляя в формулу (27) значения коэффициентов усиления 
; 
; 
,
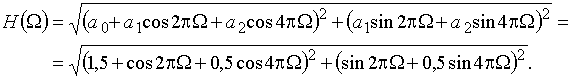
График АЧХ изображен на рис. 51.
Пример 17.3. Изменим коэффициенты усиления в предыдущем примере. Выберем 
, 
. Вновь найдем выражение 
и построим график его амплитудно-частотной характеристики.
Заменим в формуле для 
, полученной в Примере 17.2, значения коэффициентов 
, 
и 
. Получим
.
График АЧХ изображен на рис. 52. Из графика видно, что нерекурсивная цепь с такими значениями коэффициентов усиления - это режекторный фильтр.
Сопоставляя результаты расчета и графики, приведенные в Примерах 17.2 и 17.3, можно сделать важный вывод. Одним из основных преимуществ цифровых фильтров является простота их перестройки. Для получения фильтров разного функционального назначения достаточно изменить коэффициенты усиления.
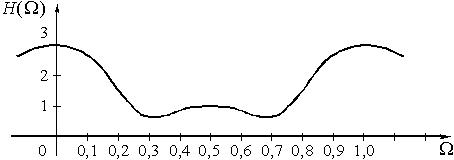
Рис. 51
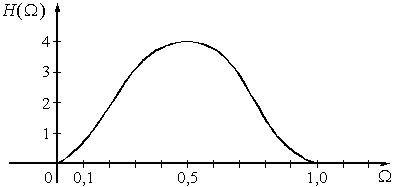
Рис. 52
Самоконтроль
1. Как перейти от передаточной функции к частотной характеристике?
2. Как определить амплитудно-частотную и фазо-частотную характеристики дискретной цепи?
3. Запишите выражение для амплитудно-частотной характеристики цепи, разностное уравнение которой имеет вид 
.