1.5.1. Случайные переменные

1.5.1.1. Среднее по ансамблю

1.5.2. Случайные процессы

1.5.2.1. Статистическое среднее случайного процесса

1.5.2.2. Стационарность

1.5.2.3. Автокорреляция случайных процессов, стационарных в широком смысле

1.5.3. Усреднение по времени и эргодичность

1.5.4. Спектральная плотность мощности и автокорреляция случайного процесса

1.5.5. Шум в системах связи

1.5.5.1. Белый шум

Основной задачей системы связи является передача информации по каналу связи. Все полезные сигналы сообщений появляются случайным образом, т.е. приемник не знает заранее, какой из возможных символов сообщений будет передан. Кроме того, вследствие различных электрических процессов возникают шумы, которые сопровождают информационные сигналы. Следовательно, нам нужен эффективный способ описания случайных сигналов.

1.5.1. Случайные переменные

Пусть случайная переменная Х(А) представляет функциональное отношение между случайным событием А и действительным числом. Для удобства записи обозначим случайную переменную через X, а ее функциональную зависимость от А будем считать явной. Случайная переменная может быть дискретной или непрерывной. Распределение случайной переменной X находится выражением:

, (1.24)

где - вероятность того, что значение принимаемой; случайной переменной X меньше действительного числа х или равно ему. Функция распределения имеет следующие свойства.

1.

2. если

3.

4.

Еще одной полезной функцией, связанной со случайной переменной X, является плотность вероятности, которая записывается следующим образом.

(1.25,а)

Как и в случае функции распределения, плотность вероятности - это функция действительного числа х. Название «функция плотности» появилось вследствие того, что вероятность события равна следующему.

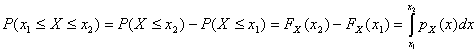(1.25,б)

Используя уравнение (1.25,6), можно приближенно записать вероятность того, что случайная переменная X имеет значение, принадлежащее очень малому промежутку между и .

(1.25,в)

Таким образом, в пределе при , стремящемся к нулю, мы можем записать следующее.

(1.25,г)

Плотность вероятности имеет следующие свойства.

1.

2. .

Таким образом, плотность вероятности всегда неотрицательна и имеет единичную площадь. В тексте книги мы будем использовать запись для обозначения плотности вероятности для непрерывной случайной переменной. Для удобства записи мы часто будем опускать индекс X и писать просто . Если случайная переменная X может принимать только дискретные значения, для обозначения плотности вероятности мы будем использовать запись .

1.5.1.1. Среднее по ансамблю

Среднее значение (mean value) , или математическое ожидание (expected value), случайной переменной X определяется выражением

, (1.26)

где именуется оператором математического ожидания (expected value operator). Моментом n-го порядка распределения вероятностей случайной переменной X называется следующая величина.

(1.27)

Для анализа систем связи важны первые два момента переменной X. Так, при n=1 уравнение (1.27) дает момент , рассмотренный выше, а при n= 1 - среднеквадратическое значение X.

(1.28)

Можно также определить центральные моменты, представляющие собой моменты разности X и . Центральный момент второго порядка (называемый также дисперсией) равен следующему.

(1.29)

Дисперсия X также записывается как , а квадратный корень из этой величины, , называется среднеквадратическим отклонением X. Дисперсия - это мера «разброса» случайной переменной X. Задание дисперсии случайной переменной ограничивает ширину функции плотности вероятности. Дисперсия и среднеквадратическое значение связаны следующим соотношением.

Таким образом, дисперсия равна разности среднеквадратического значения и квадрата среднего значения.

1.5.2. Случайные процессы

Случайный процесс можно рассматривать как функцию двух переменных: события А и времени. На рис. 1.5 представлен пример случайного процесса. Показаны N выборочных функций времени . Каждую из выборочных функций можно рассматривать как выход отдельного генератора шума. Для каждого события имеем единственную функцию времени (т.е. выборочную функцию). Совокупность всех выборочных функций называется ансамблем. В любой определенный момент времени , - это случайная переменная , значение которой зависит от события. И последнее, для конкретного события и для конкретного момента времени , - это обычное число. Для удобства записи будем обозначать случайный процесс через X(t), а функциональную зависимость от А будем считать явной.

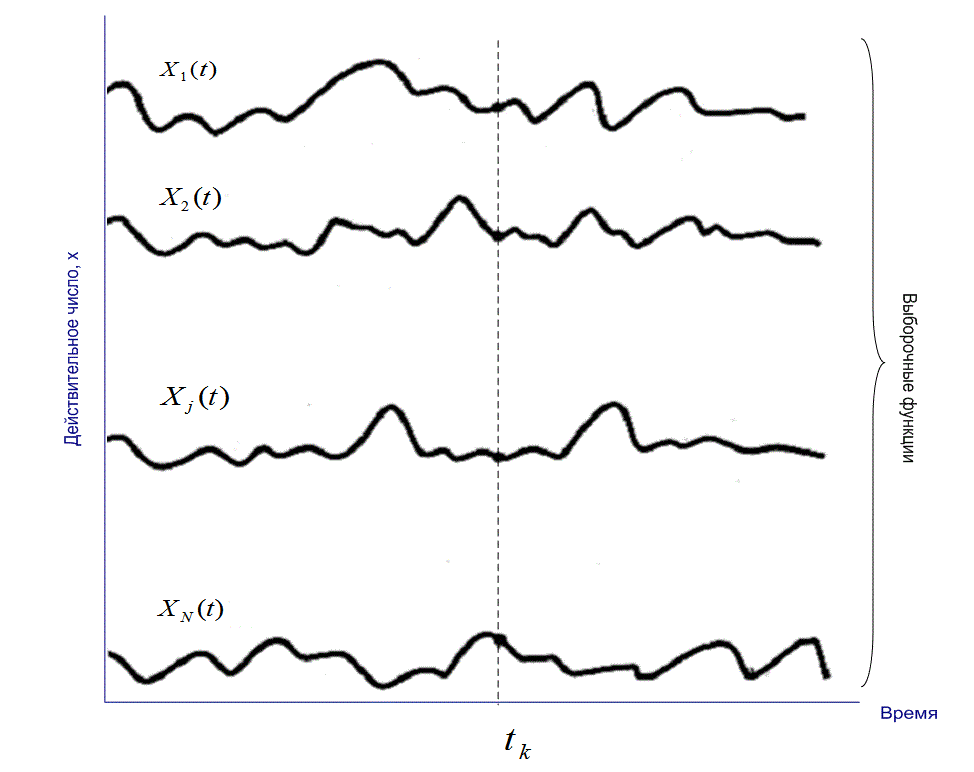
Рис.1.5. Случайный процесс шума

1.5.2.1. Статистическое среднее случайного процесса

Поскольку значение случайного процесса в каждый последующий момент времени неизвестно, случайный процесс, функции распределения которого непрерывны, можно описать статистически через плотность вероятности. Вообще, в различные моменты времени эта функция для случайного процесса будет иметь разный вид. В большинстве случаев эмпирически определить распределение вероятностей случайного процесса нереально. В то же время для нужд систем связи часто достаточно частичного описания, включающего среднее и функцию автокорреляции. Итак, определим среднее случайного процесса X(t) как

, (1.30)

где - случайная переменная, полученная при рассмотрении случайного процесса в момент времени , a - плотность вероятности (плотность по ансамблю событий в момент времени ).

Определим автокорреляционную функцию случайного процесса X(t) как функцию двух переменных и

, (1.31)

где и - случайные переменные, получаемые при рассмотрении X(t) в моменты времени и соответственно. Автокорреляционная функция - это мера связи двух временных выборок одного случайного процесса.

1.5.2.2. Стационарность

Случайный процесс X(t) называется стационарным в строгом смысле, если ни на одну из его статистик не влияет перенос начала отсчета времени. Случайный процесс именуется стационарным в широком смысле, если две его статистики, среднее и автокорреляционная функция, не меняются при переносе начала отсчета времени. Таким образом, процесс является стационарным в широком смысле, если

(1.32)

и

(1.33)

Стационарность в строгом смысле подразумевает стационарность в широком смысле, но не наоборот. Большинство полезных результатов теории связи основывается на предположении, что случайные информационные сигналы и шум являются стационарными в широком смысле. С практической точки зрения случайный процесс не обязательно всегда должен быть стационарным, достаточно стационарности в некотором наблюдаемом интервале времени, представляющем практический интерес.

Для стационарных процессов автокорреляционная функция в уравнении (1.33) зависит не от времени, а только от разности . Иными словами, все пары значений X(t) в моменты времени, разделенные промежутком , имеют одинаковое корреляционное значение. Следовательно, для стационарных систем функцию можно записывать просто как .

1.5.2.3. Автокорреляция случайных процессов, стационарных в широком смысле

Как дисперсия предлагает меру случайности для случайных переменных, так и автокорреляционная функция предлагает подобную меру для случайных процессов. Для процессов, стационарных в широком смысле, автокорреляционная функция зависит только от разности времен .

для (1.34)

Для стационарного в широком смысле процесса с нулевым средним, функция показывает, насколько статистически коррелируют случайные величины процесса, разделенные секундами. Другими словами, дает информацию о частотной характеристике, связанной со случайным процессом. Если меняется медленно по мере увеличения от нуля до некоторого значения, это показывает, что в среднем выборочные значения X(t), взятые в моменты времени и , практически равны. Следовательно, мы вправе ожидать, что в частотном представлении X(t) будут преобладать низкие частоты. С другой стороны, если быстро уменьшается по мере увеличения , стоит ожидать, что X(t) будет быстро меняться по времени и, следовательно, будет включать преимущественно высокие частоты.

Автокорреляционная функция стационарного в широком смысле процесса, принимающего действительные значения, имеет следующие свойства.

1. симметрия по относительно нуля

2. для всех максимальное значение в нуле

3. автокорреляция и спектральная плотность мощности являются Фурье-образами друг друга

4. значение в нуле равно средней мощности сигнала

1.5.3. Усреднение по времени и эргодичность

Для вычисления и путем усреднения по ансамблю нам нужно усреднить их по всем выборочным функциям процесса, и, значит, нам потребуется полная информация о взаимном распределении функций плотности вероятности в первом и втором приближениях. В общем случае, как правило, такая информация недоступна.

Если случайный процесс принадлежит к особому классу, называемому классом эргодических процессов, его среднее по времени равно среднему по ансамблю и статистические свойства процесса можно определить путем усреднения по времени одной выборочной функции процесса. Чтобы случайный процесс был эргодическим, он должен быть стационарным в строгом смысле (обратное не обязательно). Впрочем, для систем связи, где нам достаточно стационарности в широком смысле, нас интересуют только среднее и автокорреляционная функция.

Говорят, что случайный процесс является эргодическим по отношению к среднему значению, если

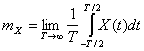(1.35)

и эргодическим по отношению к автокорреляционной функции, если

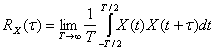(1.36)

Проверка случайного процесса на эргодичность обычно весьма непроста. На практике, как правило, используется интуитивное предположение о целесообразности замены средних по ансамблю средними по времени. При анализе большинства сигналов в каналах связи (при отсутствии импульсных эффектов) разумным будет предположение, что случайные сигналы являются эргодическими по отношению к автокорреляционной функции. Поскольку для эргодических процессов средние по времени равны средним по ансамблю, фундаментальные электротехнические параметры, такие как амплитуда постоянной составляющей, среднеквадратическое значение и средняя мощность, могут быть связаны с моментами эргодического случайного процесса.

1. Величина равна постоянной составляющей сигнала.

2. Величина равна нормированной мощности постоянной составляющей.

3. Момент второго порядка X(t), , равен общей средней нормированной мощности.

4. Величина равна среднеквадратическому значению сигнала, выраженного через ток или напряжение.

5. Дисперсия равна средней нормированной мощности переменного сигнала.

6. Если среднее процесса равно нулю (т.е. ), то , а дисперсия равна среднеквадратическому значению или (другая формулировка) дисперсия представляет общую мощность в нормированной нагрузке.

7. Среднеквадратическое отклонение является среднеквадратическим значением переменного сигнала.

8. Если , то - это среднеквадратическое значение сигнала.

1.5.4. Спектральная плотность мощности и автокорреляция случайного процесса

Случайный процесс X(t) можно отнести к периодическому сигналу, имеющему такую спектральную плотность мощности , как указано в уравнении (1.20). Функция особенно полезна в системах связи, поскольку она описывает распределение мощности сигнала по диапазону частот. Спектральная плотность мощности позволяет оценить мощность сигнала, который будет передаваться через сеть с известными частотными характеристиками. Основные свойства функций спектральной плотности мощности можно сформулировать следующим образом.

1. всегда принимает действительные значения

2. для X(t), принимающих действительные значения

3. автокорреляция и спектральная плотность мощности являются Фурье-образами друг друга

4. 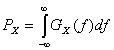связь между средней нормированной мощностью и спектральной плотностью мощности

На рис. 1.6 приведено визуальное представление автокорреляционной функции и функции спектральной плотности мощности. Что означает термин «корреляция»? Когда мы интересуемся корреляцией двух явлений, спрашиваем, насколько близко они соотносятся по поведению или виду и насколько они совпадают. В математике автокорреляционная функция сигнала (во временной области) описывает соответствие сигнала самому себе, смещенному на некоторый промежуток времени. Точная копия считается созданной и локализированной на минус бесконечности. Затем мы последовательно перемещаем копию в положительном направлении временной оси и задаем вопрос, насколько они (исходная версия и копия) соответствуют друг другу. Затем мы перемещаем копию еще на один шаг в положительном направлении и задаем вопрос, насколько они совпадают теперь, и т.д. Корреляция между двумя сигналами изображается как функция времени, обозначаемого ; при этом время можно рассматривать как параметр сканирования.

На рис. 1.6, а-г изображена описанная выше ситуация в некоторые моменты времени. Рис. 1.6, а иллюстрирует отдельный сигнал стационарного в широком смысле случайного процесса X(t). Сигнал представляет собой случайную двоичную последовательность с положительными и отрицательными (биполярными) импульсами единичной амплитуды. Положительные и отрицательные импульсы появляются с равной вероятностью. Длительность каждого импульса (двоичной цифры) равна Т секунд, а среднее, или величина постоянной составляющей случайной последовательности, равно нулю. На рис. 1.6, б показана та же последовательность, смещенная во времени на секунд. Согласно принятым обозначениям, эта последовательность обозначается . Предположим, что процесс X(t) является эргодическим по отношению к автокорреляционной функции, поэтому для нахождения мы можем использовать усреднение по времени вместо усреднения по ансамблю. Значение получается при перемножении двух последовательностей X(t) и с последующим нахождением среднего с помощью уравнения (1.36), которое справедливо для эргодических процессов только в пределе. Впрочем, интегрирование по целому числу периодов может дать нам некоторую оценку . Отметим, что может быть получено при смещении X(t) как в положительном, так и отрицательном направлении. Подобный случай иллюстрирует рис. 1.6, в, на котором использована исходная выборочная последовательность (рис. 1.6, а) и ее смещенная копия (рис. 1.6, б). Заштрихованные области под кривой произведения вносят положительный вклад в произведение, а серые области - отрицательный. Интегрирование по времени передачи импульсов дает точку на кривой . Последовательность может далее смещаться на и каждое такое смещение будет давать точку на общей автокорреляционной функции , показанной на рис. 1.6, г. Иными словами, каждой случайной последовательности биполярных импульсов соответствует автокорреляционная точка на общей кривой, приведенной на рис. 1.6, г. Максимум функции находится в точке (наилучшее соответствие имеет место при , равном нулю, поскольку для всех ), и функция спадает по мере роста . На рис. 1.6, г показаны точки, соответствующие и .

Аналитическое выражение для автокорреляционной функции , приведенной на рис. 1.6, г, имеет следующий вид [1].

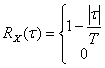
(1.37)

Отметим, что автокорреляционная функция дает нам информацию о частоте; она сообщает нам кое-что о полосе сигнала. В то же время автокорреляция - это временная функция; в формуле (1.37) отсутствуют члены, зависящие от частоты. Так как же она дает нам информацию о полосе сигнала?

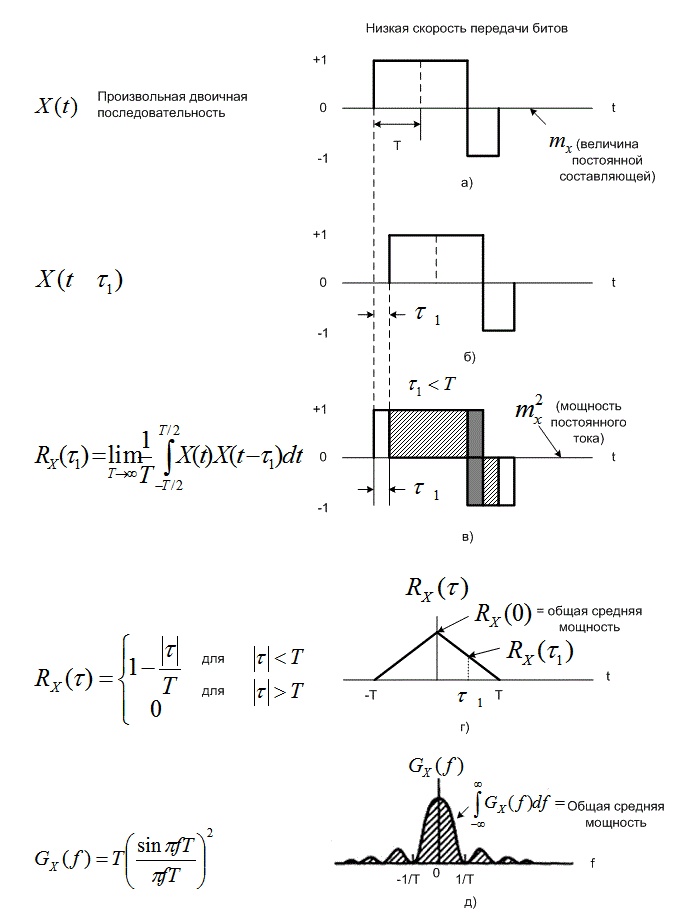
Рис.1.6. Автокорреляция и спектральная плотность мощности

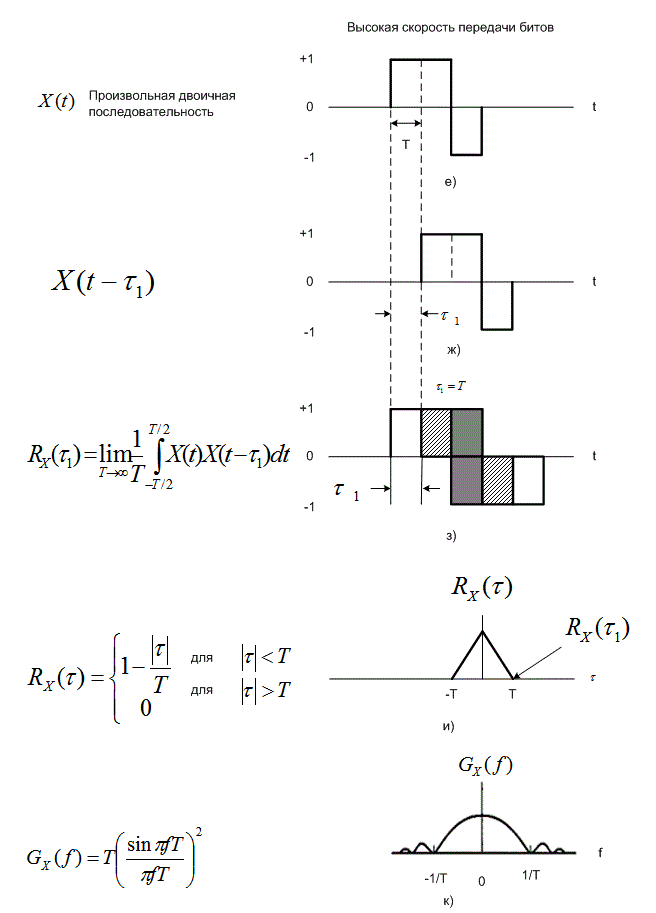
Рис.1.6. Автокорреляция и спектральная плотность мощности (окончание)

Предположим, что сигнал перемещается очень медленно (сигнал имеет малую ширину полосы). Если мы будем смещать копию сигнала вдоль оси , задавая на каждом этапе смещения вопрос, насколько соответствуют друг другу копия и оригинал, соответствие достаточно долго будет довольно сильным. Другими словами, треугольная автокорреляционная функция (рис. 1.6, г и формула 1.37) будет медленно спадать с ростом . Предположим теперь, что сигнал меняется достаточно быстро (т.е. имеем большую полосу). В этом случае даже небольшое изменение приведет к тому, что корреляция будет нулевой и автокорреляционная функция будет иметь очень узкую форму. Следовательно, сравнение автокорреляционных функций по форме дает нам некоторую информацию о ширине полосы сигнала. Функция спадает постепенно? В этом случае имеем сигнал с узкой полосой. Форма функции напоминает узкий пик? Тогда сигнал имеет широкую полосу.

Автокорреляционная функция позволяет явно выражать спектральную плотность мощности случайного сигнала. Поскольку спектральная плотность мощности и автокорреляционная функция являются Фурье-образами друг друга, спектральную плотность мощности, , случайной последовательности биполярных импульсов можно найти как Фурье-преобразование функции , аналитическое выражение которой дано в уравнении (1.37). Для этого можно использовать табл. А.1. Заметим, что

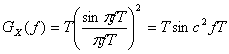(1.38)

где

(1.39)

Общий вид функции показан на рис. 1.6, д.

Отметим, что площадь под кривой спектральной плотности мощности представляет собой среднюю мощность сигнала. Одной из удобных мер ширины полосы является ширина основного спектрального лепестка (см. раздел 1.7.2). На рис. 1.6, д показано, что ширина полосы сигнала связана с обратной длительностью символа или шириной импульса. Рис. 1.6, е-к формально повторяют рис. 1.6, а-д, за исключением того, что на последующих рисунках длительность импульса меньше. Отметим, что для более коротких импульсов функция .уже (рис. 1.6, и), чем для более длительных (рис. 1.6, г). На рис. 1.6, и ; другими словами, в случае меньшей длительности импульса смещения на , достаточно для создания нулевого соответствия или для полной потери корреляции между смещенными последовательностями. Поскольку на рис. 1.6, е длительность импульса Т меньше (выше скорость передачи импульса), чем на рис. 1.6, а, занятость полосы на рис. 1.6, к больше занятости полосы для более низкой частоты импульсов, показанной на рис. 1.6, д.

1.5.5. Шум в системах связи

Термин «шум» обозначает нежелательные электрические сигналы, которые всегда присутствуют в электрических системах. Наличие шума, наложенного на сигнал, «затеняет», или маскирует, сигнал; это ограничивает способность приемника принимать точные решения о значении символов, а следовательно, ограничивает скорость передачи информации. Природа шумов различна и включает как естественные, так и искусственные источники. Искусственные шумы - это шумы искрового зажигания, коммутационные импульсные помехи и шумы от других родственных источников электромагнитного излучения. Естественные шумы исходят от атмосферы, солнца и других галактических источников.

Хорошее техническое проектирование может устранить большинство шумов или их нежелательные эффекты посредством фильтрации, экранирования, выбора модуляции и оптимального местоположения приемника. Например, чувствительные радиоастрономические измерения проводятся, как правило, в отдаленных пустынных местах, вдали от естественных источников шума. Впрочем, существует один естественный шум, называемый тепловым, который устранить нельзя. Тепловой шум [4, 5] вызывается тепловым движением электронов во всех диссипативных компонентах - резисторах, проводниках и т.п. Те же электроны, которые отвечают за электропроводимость, являются причиной теплового шума.

Тепловой шум можно описать как гауссов случайный процесс с нулевым средним. Гауссов процесс n(t) - это случайная функция, значение которой и в произвольный момент времени t статистически характеризуется гауссовой функцией плотности вероятностей:

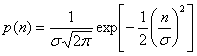, (1.40)

где - дисперсия n. Нормированная гауссова функция плотности процесса с нулевым средним получается в предположении, что . Схематически нормированная функция плотности вероятностей показана на рис. 1.7.

Далее мы часто будем представлять случайный сигнал как сумму случайной переменной, выражающей гауссов шум, и сигнала канала связи.

Здесь - случайный сигнал, а - сигнал в канале связи, а n - случайная переменная, выражающая гауссов шум. Тогда функция плотности вероятности выражается как

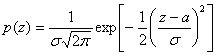, (1.41)

где, как и выше, - дисперсия n.

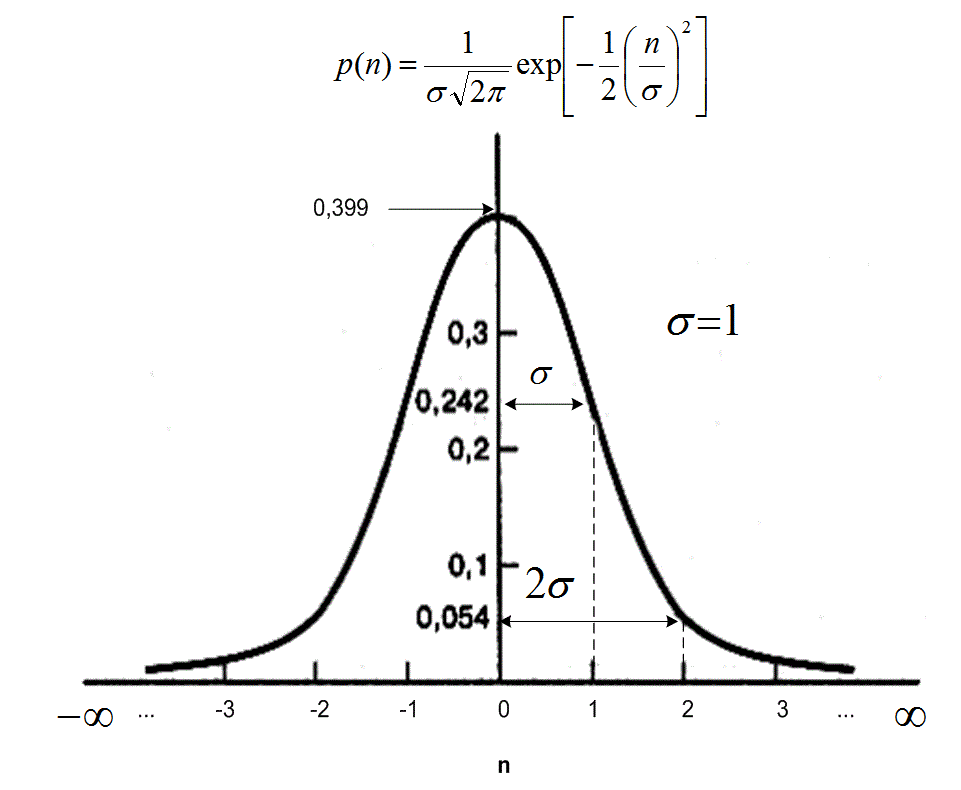
Рис.1.7. Нормированная () гауссова функция плотности вероятности

Гауссово распределение часто используется как модель шума в системе, поскольку существует центральная граничная теорема [3], утверждающая, что при весьма общих условиях распределение вероятностей суммы j статистически независимых случайных переменных подчиняется гауссовому распределению , причем вид отдельных функций распределения не имеет значения. Таким образом, даже если отдельные механизмы шума будут иметь негауссово распределение, совокупность многих таких механизмов будет стремиться к гауссовому распределению.

1.5.5.1. Белый шум

Основной спектральной характеристикой теплового шума является то, что его спектральная плотность мощности одинакова для всех частот, представляющих интерес для большинства систем связи; другими словами, источник теплового шума на всех частотах излучает с равной мощностью на единицу ширины полосы - от постоянной составляющей до частоты порядка Гц. Следовательно, простая модель теплового шума предполагает, что его спектральная плотность мощности равномерна для всех частот, как показано на рис. 1.8, а, и записывается в следующем виде.

(1.42)

Здесь коэффициент 2 включен для того, чтобы показать, что - двусторонняя спектральная плотность мощности. Когда мощность шума имеет такую единообразную спектральную плотность, мы называем этот шум белым. Прилагательное «белый» используется в том же смысле, что и для белого света, содержащего равные доли всех частот видимого диапазона электромагнитного излучения.

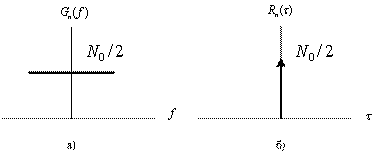
Рис.1.8. Белый шум: а) спектральная плотность мощности;

б) автокорреляционная функция

Автокорреляционная функция белого шума дается обратным преобразованием Фурье спектральной плотности мощности шума (см. табл. А.1) и записывается следующим образом.

(1.43)

Таким образом, автокорреляция белого шума - это дельта-функция, взвешенная множителем и находящаяся в точке , как показано на рис. 1.8, б. Отметим, что равна нулю для , т.е. две различные выборки белого шума не коррелируют, вне зависимости от того, насколько близко они находятся.

Средняя мощность белого шума бесконечна, поскольку бесконечна ширина полосы белого шума. Это можно увидеть, получив из уравнений (1.19) и (1.42) следующее выражение.

(1.44)

Хотя белый шум представляет собой весьма полезную абстракцию, ни один процесс шума в действительности не может быть белым; впрочем, шум, появляющийся во многих реальных системах, можно предположительно считать белым. Наблюдать такой шум мы можем только после того, как он пройдет через реальную систему, имеющую конечную ширину полосы. Следовательно, пока ширина полосы шума существенно больше ширины полосы, используемой системой, можно считать, что шум имеет бесконечную ширину полосы.

Дельта-функция в уравнении (1.43) означает, что сигнал шума n(t) абсолютно не коррелирует с собственной смещенной версией для любого . Уравнение (1.43) показывает, что любые две выборки процесса белого шума не коррелируют. Поскольку тепловой шум - это гауссов процесс и его выборки не коррелируют, выборки шума также являются независимыми [3]. Таким образом, воздействие канала с аддитивным белым гауссовым шумом на процесс обнаружения состоит в том, что шум независимо воздействует на каждый переданный символ. Такой канал называется каналом без памяти. Термин «аддитивный» означает, что шум просто накладывается на сигнал или добавляется к нему - никаких мультипликативных механизмов не существует.

Поскольку тепловой шум присутствует во всех системах связи и для большинства систем является заметным источником шума, характеристики теплового шума (аддитивный, белый и гауссов) часто применяются для моделирования шума в системах связи. Поскольку гауссов шум с нулевым средним полностью характеризуется его дисперсией, эту модель особенно просто использовать при обнаружении сигналов и проектировании оптимальных приемников. В данной книге мы будем считать (если не оговорено противное), что система подвергается искажению со стороны аддитивного белого гауссового шума с нулевым средним, хотя иногда такое упрощение будет чересчур сильным.