12.2.1. Свойства случайной последовательности
Системы связи расширенного спектра с передачей опорного сигнала (transmitted reference — TR) могут использовать истинно случайный кодовый сигнал для расширения и сужения, поскольку кодовый сигнал и модулированный данными кодовый сигнал одновременно передаются в разных областях спектра. Метод хранения опорного сигнала (stored reference — SR) не позволяет использовать истинно случайные кодовые сигналы, поскольку код должен храниться или генерироваться приемником. В системах SR должен применяться псевдошумовой (pseudonoise) или псевдослучайный (pseudorandom) кодовый сигнал.
В чем отличие псевдослучайного кода от истинно случайного? Случайная последовательность непредсказуема и может быть описана только в статистическом смысле. Псевдослучайный код на самом деле не является случайным — это детерминированный периодический сигнал, известный передатчику и приемнику. Так почему же он называется "псевдослучайным"? Причина в том, что он имеет все статистические свойства дискретного белого шума. Для "неуполномоченного" пользователя такой сигнал будет казаться абсолютно случайным.
12.2.1. Свойства случайной последовательности
Каким должен быть псевдослучайный код, чтобы казаться истинно случайным? Существует три основных свойства любой периодической двоичной последовательности, которые могут быть использованы в качестве проверки на случайность.
1. Сбалансированность. Для каждого интервала последовательности количество двоичных единиц должно отличаться от числа двоичных нулей не больше чем на на один элемент.
2. Цикличность. Циклом называют непрерывную последовательность одинаковых двоичных чисел. Появление иной двоичной цифры автоматически начинает новый цикл. Длина цикла равна количеству цифр в нем. Желательно, чтобы в каждом фрагменте последовательности приблизительно половину составляли циклы обоих типов длиной 1, приблизительно одну четверть— длиной 2, приблизительно одну восьмую — длиной 3 и т. д.
3. Корреляция. Если часть последовательности и ее циклично сдвинутая копия поэлементно сравниваются, желательно, чтобы число совпадений отличалось от числа несовпадений не более чем на единицу.
В следующем разделе для проверки данных свойств будет сгенерирована псевдослучайная последовательность.
12.2.2. Последовательности, генерируемые регистром сдвига
Рассмотрим линейный регистр сдвига с обратной связью (рис. 12.7), который состоит из четырехразрядного регистра для хранения и сдвига, сумматора по модулю 2 (операция суммирования по модулю 2 была определена в разделе 2.9.3), а также контура обратной связи с входом регистра. Работа регистра сдвига управляется последовательностью синхронизирующих импульсов (не показанных на рисунке). С каждым импульсом содержимое регистров сдвигается на одну позицию вправо, а содержимое регистров Х3и Х4 суммируется по модулю 2 (линейная операция). Результат суммирования по обратной связи подается на разряд Х1. Последовательность, генерируемая регистром сдвига, — это, по определению, выход последнего регистра (в данном случае Х4).
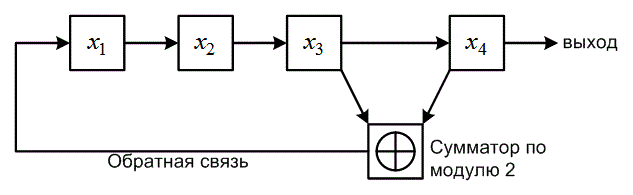
Рис.12.7. Пример линейного регистра сдвига с обратной связью
Предположим, что разряд X, содержит единицу, а все остальные разряды — нули, т.е. начальным состоянием регистра является 1000. В соответствии с рис. 12.7, последующие состояния регистра будут следующими.
1000 0100 0010 1001 1100 0110 1011 0101
1010 1101 1110 1111 0111 0011 0001 1000
Поскольку последнее состояние, 1000, идентично начальному, видим, что приведенная последовательность повторяется регистром через каждые 15 тактов. Выходная последовательность определяется содержимым разряда Х4 на каждом такте. Эта последовательность имеет следующий вид.
0 0 0 1 0 0 1 1 0 1 0 1 1 1 1
Здесь крайний "левый бит является самым ранним. Проверим полученную последовательность на предмет соответствия критериям, приведенным в предыдущем разделе. Последовательность содержит семь нулей и восемь единиц, что соответствует условию сбалансированности. Рассмотрим циклы нулей — всего их четыре, причем половина их имеет длину 1, а одна четвертая — длину 2. То же получаем для циклов единиц. Последовательность слишком коротка, чтобы продолжать проверку, но видно, что условие цикличности выполняется. Условие корреляции будет проверено в разделе 12.2.3.
Последовательность, сгенерированная регистром сдвига, зависит от количества разрядов, места подсоединения отводов обратной связи и начальных условий. Последовательности на выходе генератора могут классифицироваться как имеющие максимальную или не максимальную длину. Период повторения (в тактах) последовательности максимальной длины, генерируемой n-каскадным линейным регистром сдвига с обратной связью, равен следующему.
![]() (12.3)
(12.3)
Очевидно, что последовательность, сгенерированная регистром сдвига на рис. 12.7, является примером последовательности с максимальной длиной. Если длина последовательности меньше (![]() ), говорят, что последовательность имеет не максимальную длину.
), говорят, что последовательность имеет не максимальную длину.
12.2.3. Автокорреляционная функция псевдослучайного сигнала
Автокорреляционная функция Rx(![]() ) периодического сигнала x(t) с периодом Т0была представлена в уравнении (1.23) и приводится ниже в нормированной форме.
) периодического сигнала x(t) с периодом Т0была представлена в уравнении (1.23) и приводится ниже в нормированной форме.
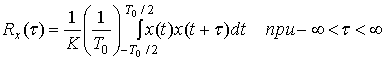 , (12.4)
, (12.4)
где
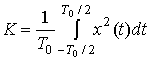 (12.5)
(12.5)
Если x(t) является периодическим импульсным сигналом, представляющим псевдослучайный код, каждый из элементарных импульсов такого сигнала называют кодовым символом (code symbol) или элементарным сигналом (chip). Нормированная автокорреляционная функция псевдослучайного сигнала с единичной длительностью элементарного сигнала и периодом р элементарных сигналов может быть записана следующим образом.
 (12.6)
(12.6)
График нормированной автокорреляционной функции последовательности максимальной длины ![]() показан на рис. 12.8. Очевидно, что для
показан на рис. 12.8. Очевидно, что для ![]() =0, т.е. когда сигнал x(t) и его копия идеально совпадают,
=0, т.е. когда сигнал x(t) и его копия идеально совпадают, ![]() = 1. В то же время для любого циклического сдвига между x(t) и x(t+
= 1. В то же время для любого циклического сдвига между x(t) и x(t+![]() ) при (1<
) при (1<![]() <р) автокорреляционная функция равна -1|р (для больших значений р последовательности практически декоррелируют между собой при сдвиге на один элементарный сигнал).
<р) автокорреляционная функция равна -1|р (для больших значений р последовательности практически декоррелируют между собой при сдвиге на один элементарный сигнал).
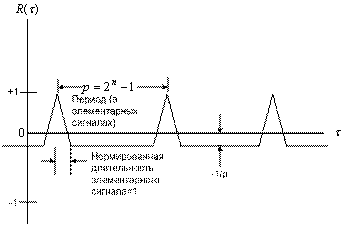
Рис. 12.8. Автокорреляционная функция псевдослучайной последовательности
Теперь легко можно провести проверку свойства корреляции для псевдослучайной последовательности, сгенерированной регистром сдвига на рис. 12.7. Запишем выходную последовательность и ее модификацию со сдвигом на один регистр вправо.
0 0 0 1 0 0 1 1 0 1 0 1 1 1 1
1 0 0 0 1 0 0 1 1 0 1 0 1 1 1
d a a d d a d a d d d d a a a
Совпадение цифр отмечено символом а, а несовпадение — d. Согласно уравнению (12.6) автокорреляционная функция при подобном сдвиге на один элементарный сигнал равна следующему.
![]()
Любой циклический сдвиг, который приводит к отклонению от идеальной синхронизации, дает значение автокорреляционной функции -1/р. Следовательно, третье свойство псевдослучайной последовательности в данном случае выполняется.

