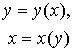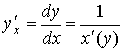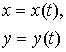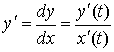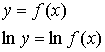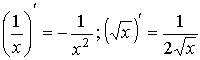6.2. Основные правила дифференцирования
6.3. Производные основных элементарных функций
6.1. Определение производной
Пусть ![]() - определена и непрерывна в окрестности x0
- определена и непрерывна в окрестности x0
Производная функции в точке x0 и ее обозначения:
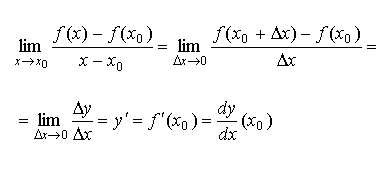
6.2. Основные правила дифференцирования
|
Наименование |
Функция |
Производная |
| Линейная комбинация двух функций
Частные случаи: a) умножение б) сумма (разность) двух функций |
|
|
| Произведение
а) двух функций б) трех функций |
|
|
| Частное двух функций |
|
|
| Сложная функция |
y=F(u), u=j (x) |
|
| Обратная функция |
|
|
| Параметрическое задание функции |
|
|
| Логарифмическое дифференцирование |
|
|
6.3. Производные основных элементарных функций
|
№ п/п |
Наименование функции |
Функция и её производная |
|
1 |
константа | |
|
2 |
степенная функция
частные случаи |
|
|
3 |
показательная функция
частный случай |
|
|
4 |
логарифмическая функция
частный случай |
|
|
5 |
тригонометрические функции | |
|
6 |
обратные тригонометрические функции |
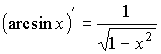 ; ;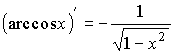 ; ;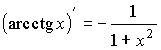 |
6.4. Гиперболические функции
|
Наименование |
Формула |
Производная |
| Гиперболический синус | 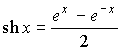 |
|
| Гиперболический косинус формула | 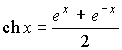 |
|
| Гиперболический тангенс | 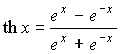 |
|
| Гиперболический котангенс | 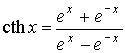 |
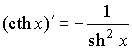 |
Обратные гиперболические функции
|
Наименование |
Формула |
Производная |
| Ареасинус | 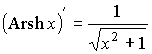 |
|
| Ареакосинус | 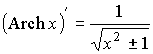 |
|
| Ареатангенс | 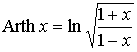 |
|
| Ареакотангенс | 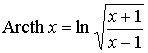 |
Графики гиперболических функций:
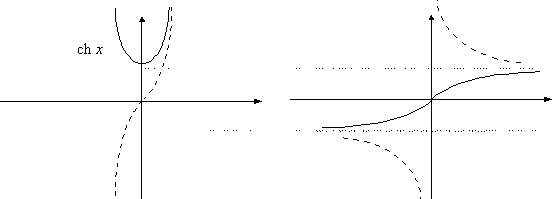
6.5. Производные высших порядков и формула Тейлора
Производная второго порядка функции y=f(x) : 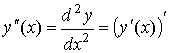
Производная n-го порядка (n-ая производная) функции y=f(x):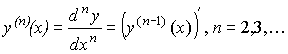
Формула Тейлора:
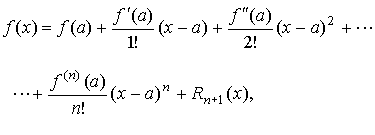
где 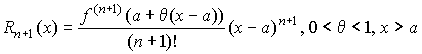
- остаточный член в форме Лагранжа.
Формула Маклорена (a=0):
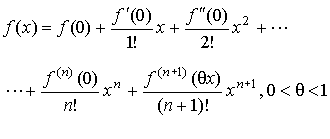
6.6. Исследование функций
План полного исследования функции:
1. Элементарное исследование:
- найти область определения и область значений;
- выяснить общие свойства: четность(нечетность), периодичность;
- найти точки пересечения с осями координат;
- определить участки знакопостоянства.
2. Исследование с помощью предела:
- найти точки разрыва и выяснить их характер;
- найти область непрерывности;
- найти вертикальные и наклонные асимптоты.
3. Исследование с помощью
:
- найти критические точки;
- определить интервалы возрастания и убывания функции;
- определить экстремумы.
4. Исследование с помощью
:
- найти точки, в которых
или не существует;
- найти участки выпуклости и вогнутости;
- определить точки перегиба.
5. Построение графика функции.
Рекомендации по применению плана исследования функции:
- Отдельные элементы исследования наносятся на график постепенно, по мере их нахождения.
- Если появляются затруднения с построением графика функции, то находятся значения функции в некоторых дополнительных точках.
- Целью исследования является описание характера поведения функции. Поэтому строится не точный график, а его приближение, на котором четко обозначены найденные элементы (экстремумы, точки перегиба, асимптоты и т.д.).
- Строго придерживаться приведенного плана необязательно; важно не упустить характерные элементы поведения функции.