10.1. ЧМ сигналы с оптимальной апериодической АКФ

Начнем краткое обсуждение задачи построения ЧМ сигналов с хорошими корреляционными свойствами с напоминания, что требование малого уровня эквивалентно минимизации числа совпадающих частот в частотном коде и его копии, сдвинутой на позиций. Очевидно, что при числе чипов (т.е. длине), не большей числа доступных частот , нулевой уровень боковых лепестков достигается тривиальным использованием частотного кода, все элементы которого различны. Практически, однако, интереснее ситуация, когда , так что среди элементов имеются повторяющиеся, и, следовательно, по крайней мере, одно совпадение частот в сдвинутых копиях частотного кода неизбежно, т.е. .

Одним из широко используемых способов задания ЧМ сигналов является их описание с помощью массива (матрицы) размера , в которой горизонтальное и вертикальное направления отождествляются со временем и частотой соответственно, а определяет объем частотного алфавита (т.е. число различных частот, используемых при модуляции). В –м вертикальном столбце этой матрицы помечается только единственный элемент (например, точкой или закрашиванием), что отвечает частоте –го чипа.

Пример 10.1.1. Матрица, изображенная на рисунке, отвечает закону модуляции ЧМ сигнала длиной и .

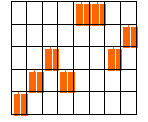
Таким образом, минимизация означает построение решетки с наименьшим числом совпадений меток в исходной решетке и ее копии, сдвинутой по горизонтали на позиций. Одной из наиболее характерных задач этого рода является синтез так называемых радарных решеток – решеток с единственной помеченной клеткой в каждом столбце и , т.е. с числом упомянутых совпадений не более одного. Вполне объясним интерес к отысканию радарных решеток максимальной длины при фиксированном объеме частотного алфавита , поскольку это равносильно минимизации при ограничениях на частотный ресурс. Определим простейшую верхнюю границу длины радарной решетки.

Рассмотрим последовательность и заметим, что для получения не более одного совпадения все разности между номерами позиций с одинаковыми частотами должны быть различными. Действительно, пусть и . Тогда в исходной последовательности и ее копии, сдвинутой на позиций, будет не менее двух совпадений. Обозначим через число символов (частот) среди , повторяющихся раз. Тогда

.

Подсчитаем теперь число возможных разностей между номерами позиций с идентичными частотами. Имеется повторений какой-то частоты, и, значит, таких разностей именно для этой частоты. Поскольку имеется частот, повторяющихся раз, то общее число названных разностей составит , и, так как повторения среди этих разностей запрещены, должно выполняться неравенство

,

правая часть которого есть максимальное число неравных положительных разностей на числовом множестве . Трином не имеет действительных корней и, следовательно, положителен при любом . Поэтому сумма

,

что с учетом ранее введенных обозначений дает , или

.

Полученная граница не является точной. Известна более точная граница, которая в асимптотической версии имеет вид

,

что понижает правую часть предшествующего выражения приблизительно на .

Абсолютно точные, т.е. действительно достижимые, верхние границы длины известны на данный момент для значений . Для указанного диапазона максимально реализуемая длина радарных решеток определяется как

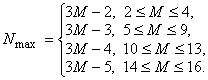
Пример 10.1.2. Частотный код {1, 2, 3, 4, 5, 6, 7, 8, 7, 4, 3, 9, 9, 5, 8, 2, 6, 5, 1, 4, 2, 1, 3, 7}, задающий номера частот из некоторого алфавита объема или, что эквивалентно, номера помеченных строк в каждом столбце решетки, имеет максимально возможную длину . Определяющее свойство радарной решетки, т.е. возможность единственного совпадения частот при всех ненулевых сдвигах, подтверждается непосредственной проверкой.

В дополнение к сказанному, известны регулярные правила построения радарных решеток длины для любого четного и для , равного произведению простых чисел вида , т.е. .

Сонарные решетки являются дальнейшим обобщением радарных, сохраняющим свойство «не более одного совпадения» для произвольной ненулевой комбинации горизонтального и вертикального сдвигов. С физической точки зрения такое требование отражает желание иметь слабую корреляцию сигнальных копий, сдвинутых как во времени, так и по частоте. Имея в виду подход к выбору шага алфавита ЧМ сигналов, частотные сдвиги, трансформирующие текущую частоту в ближайшую из алфавита, более характерны для сонаров, нежели радиолокационных систем, с чем и связана установившаяся терминология. Известен, например, ряд регулярных алгоритмов построения массивов Костаса, т.е. квадратных сонарных массивов, иначе говоря ЧМ последовательностей длины, равной числу частот.