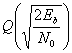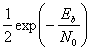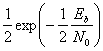4.1. Зачем нужна модуляция?

4.2. Методы цифровой полосовой модуляции

4.2.1. Векторное представление синусоиды

4.2.2. Фазовая манипуляция

4.2.3. Частотная манипуляция

4.2.4. Амплитудная манипуляция

4.2.5. Амплитудно-фазовая манипуляция

4.2.6. Амплитуда сигнала

4.3. Обнаружение сигнала в гауссовом шуме

4.3.1. Области решений

4.3.2. Корреляционный приемник

4.3.2.1. Порог двоичного решения

4.4. Когерентное обнаружение

4.4.1. Когерентное обнаружение сигналов PSK

4.4.2. Цифровой согласованный фильтр

4.4.3. Когерентное обнаружение сигналов MPSK

4.4.4. Когерентное обнаружение сигналов FSK

4.5. Некогерентное обнаружение

4.5.1. Обнаружение сигналов в дифференциальной модуляции PSK

4.5.2. Пример бинарной модуляции DPSK

4.5.3. Некогерентное обнаружение сигналов FSK

4.5.4. Расстояние между тонами для некогерентной ортогональной передачи сигналов FSK

4.5.4.1. Минимальное расстояние между тонами и ширина полосы

4.5.4.2. Дуальные соотношения

4.6. Комплексная огибающая

4.6.1. Квадратурная реализация модулятора

4.6.2. Пример модулятора D8PSK

4.6.3. Пример демодулятора D8PSK

4.7. Вероятность ошибки в бинарных системах

4.7.1. Вероятность появления ошибочного бита при когерентном обнаружении сигнала BPSK

4.7.2. Вероятность появления ошибочного бита при когерентном обнаружении сигнала в дифференциальной модуляции BPSK

4.7.3. Вероятность появления ошибочного бита при когерентном обнаружении сигнала в бинарной ортогональной модуляции FSK

4.7.4. Вероятность появления ошибочного бита при некогерентном обнаружении сигнала в бинарной ортогональной модуляции FSK

4.7.5. Вероятность появления ошибочного бита для бинарной модуляции DPSK

4.7.6. Вероятность ошибки для различных модуляций

4.8. М-арная передача сигналов и производительность

4.8.1. Идеальная достоверность передачи

4.8.2. М-арная передача сигналов

4.8.3. Векторное представление сигналов MPSK

4.8.4. Схемы BPSK и QPSK имеют одинаковые вероятности ошибки

4.8.5. Векторное представление сигналов MFSK

4.9. Вероятность символьной ошибки для М-арных систем (М > 2)

4.9.1. Вероятность символьной ошибки для модуляции MPSK

4.9.2. Вероятность символьной ошибки для модуляции MFSK

4.9.3. Зависимость вероятности битовой ошибки от вероятности символьной ошибки для ортогональных сигналов

4.9.4. Зависимость вероятности битовой ошибки от вероятности символьной ошибки для многофазных сигналов

4.9.5. Влияние межсимвольной интерференции

4.1. Зачем нужна модуляция?

Цифровая модуляция — это процесс преобразования цифровых символов в сигналы, совместимые с характеристиками канала. При узкополосной модуляции (base band modulation) эти сигналы обычно имеют вид импульсов заданной формы. В случае полосовой модуляции (band pass modulation) импульсы заданной формы модулируют синусоиду, называемую несущей волной (carrier wave), или просто несущей (carrier), затем следует передача на нужное расстояние с использованием радиочастот; для этого несущая преобразовывается в электромагнитное поле. Может возникнуть вопрос: зачем для радиопередачи узкополосных сигналов нужна несущая? Ответ звучит следующим образом. Передача электромагнитного поля через пространство выполняется с помощью антенн. Размер антенны зависит от длины волны λ, и текущей задачи. Для переносных телефонов размер антенны обычно равен λ/4, а длина волны c/f, где с — скорость света, 3 х 10⁸ м/с. Рассмотрим передачу узкополосного сигнала (скажем, имеющего частоту f=3000 Гц) путем сопряжения его непосредственно с антенной без использования несущей. Какая антенна нам понадобится? Возьмем стандарт телефонной промышленности, λ/4. Получаем, что для узкополосного сигнала 3000 Гц λ /4 = 2,5 х ¹⁰⁴ = 25 км. Итак, для передачи через пространство сигнала с частотой 3000 Гц без модулирования несущей требуется антенна размером 25 км. При этом, если узкополосная информация модулируется несущей более высокой частоты, например 900 МГц, размер антенны будет составлять порядка 8 см. Приведенные вычисления показывают, что модулирование несущей частоты, или полосовая модуляция, — это этап, необходимый для всех систем, использующих радиопередачу.

Полосовая модуляция имеет и другие важные преимущества при передаче сигналов. При использовании одного канала более чем одним сигналом, модуляция может применяться для выделения различных сигналов. Подобный метод, известный как уплотнение с частотным разделением (frequency-division multiplexing — FDM), рассматривается в главе И. Модуляция может использоваться и для минимизации последствий интерференции. Класс схем модулирования, известный как модулирование расширенным спектром, требует полосы, значительно превышающей минимальную полосу, необходимую для передачи сообщения. В главе 12 рассмотрены компромиссы, связанные с выбором полосы, снижающим интерференцию. Кроме того, модуляция может использоваться для перемещения сигнала в диапазон частот, в котором легко удовлетворяются специфические конструктивные требования, например, относящиеся к фильтрации и усилению. Примером такого применения модуляции является преобразование в приемнике радиочастотных сигналов в сигналы промежуточной частоты.

4.2. Методы цифровой полосовой модуляции

Полосовая модуляция (аналоговая или цифровая) — это процесс преобразования информационного сигнала в синусоидальную волну; при цифровой модуляции синусоида на интервале Т называется цифровым символом. Синусоиды могут отличаться по амплитуде, частоте и фазе. Таким образом, полосовую модуляцию можно определить как процесс варьирования амплитуды, частоты или фазы (или их комбинаций) радиочастотной несущей согласно передаваемой информации. В общем виде несущая записывается следующим образом.

(4.1)

Здесь A(t) — переменная во времени амплитуда, а — переменный во времени угол. Угол удобно записывать в виде

(4.2)

так что

(4.3)

где ω — угловая частота несущей, а — ее фаза. Частота может записываться как переменная f или как переменная ω. В первом случае частота измеряется в герцах (Гц), во втором — в радианах в секунду (рад/с). Эти параметры связаны следующим соотношением .

Основные типы полосовой модуляции/демодуляции перечислены на рис. 4.1. Если для обнаружения сигналов приемник использует информацию о фазе несущей, процесс называется когерентным обнаружением (coherent detection); если подобная информация не используется, процесс именуется некогерентным обнаружением (no coherent detection). Вообще, в цифровой связи термины "демодуляция" (demodulation) и "обнаружение" (detection) часто используются как синонимы, хотя демодуляция делает акцент на восстановлении сигнала, а обнаружение — на принятии решения относительно символьного значения принятого сигнала. При идеальном когерентном обнаружении приемник содержит прототипы каждого возможного сигнала. Эти сигналы-прототипы дублируют алфавит переданных сигналов по всем параметрам, даже по радиочастотной фазе. В этом случае говорят, что приемник автоматически подстраивается под фазу входящего сигнала. В процессе демодуляции приемник перемножает и интегрирует входящий сигнал с каждым прототипом (определяет корреляцию). На рис. 4.1 под общим заголовком когерентной модуляции/демодуляции перечислены: фазовая манипуляция (phase shift keying — PSK), частотная манипуляция (frequency shift keying — FSK), амплитудная манипуляция (amplitude shift keying — ASK), модуляция без разрыва фазы (continuous phase modulation — CPM) и смешанные комбинации этих модуляций. Основные форматы полосовой модуляции рассмотрены в данной главе. Некоторые специализированные форматы, такие как квадратурная фазовая манипуляция, со сдвигом (onset quadrature PSK — OQPSK), манипуляция с минимальным сдвигом (minimum shift keying — MSK), принадлежащие к классу модуляций СРМ, и квадратурная амплитудная модуляция (quadrature amplitude modulation — QAM), рассмотрены в главе 9.

Некогерентная демодуляция относится к системам, использующим демодуляторы, спроектированные для работы без знания абсолютной величины фазы входящего сигнала; следовательно, определение фазы в этом случае не требуется. Таким образом, преимуществом некогерентных систем перед когерентными является простота, а недостатком — большая вероятность ошибки (Р_Е). На рис. 4.1 под заголовком некогерентной передачи сигналов перечислены модуляции, подобные используемым при когерентной передаче: DPSK, FSK, ASK, CPM и смешанные их комбинации. Подразумевается, что для некогерентного приема информация о фазе не используется; так почему же под заголовком "некогерентная передача" указана одна из форм фазовой манипуляции? Это вызвано тем, что одну из важных форм PSK можно отнести к некогерентной (или дифференциально когерентной), поскольку она не требует согласования по фазе с принятой несущей. При использовании этой "псевдо-PSK", называемой дифференциальной фазовой манипуляцией (differential PSK — DPSK), в процессе обнаружения текущего символа в качестве опорной фазы применяется фаза предыдущего символа. Подробно этот вопрос рассмотрен в разделах 4.5.1 и 4.5.2.

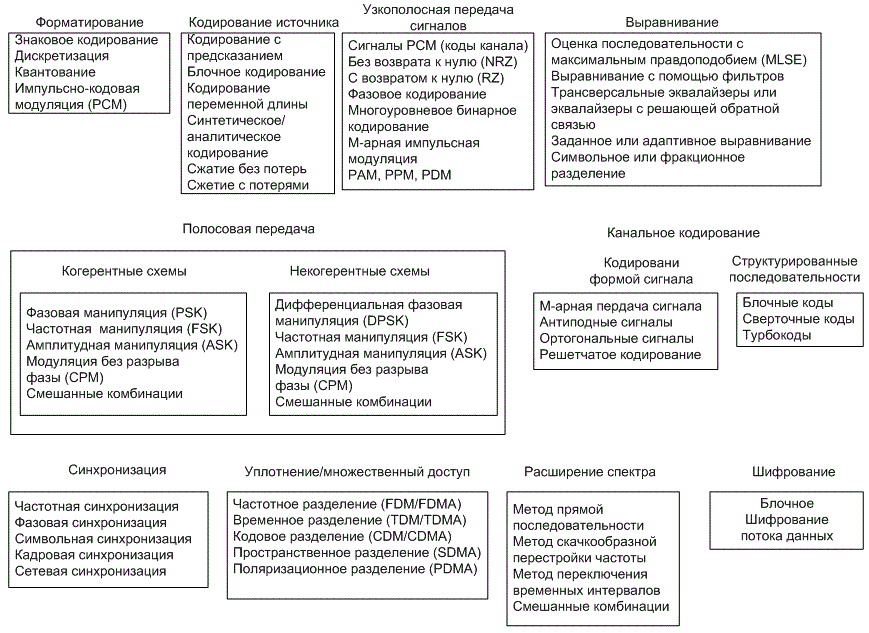
Рис 4.1. Основные преобразования цифровой связи

4.2.1. Векторное представление синусоиды

Используя известное тригонометрическое равенство, называемое теоремой Эйлера, введем комплексную запись синусоидальной несущей.

(4.4)

Возможно, кто-то чувствует себя уютнее при использовании более простой, привычной записи или . Возникает естественный вопрос: что нам дает комплексная запись? Далее будет показано (раздел 4.6), что такая форма записи облегчает описание реализации реальных модуляторов и демодуляторов. Здесь же мы рассмотрим общие преиму­щества представления несущей в комплексной форме, приведенной в формуле (4.4).

Во-первых, при комплексной записи в компактной форме, , указаны два важных компонента любой синусоидальной несущей волны, называемые взаимно ортогональными синфазной (действительной) и квадратурной (мнимой) составляющими. Во-вторых, как показано на рис. 4.2, немодулированная несущая удобно представляется в полярной системе координат в виде единичного вектора с постоянной скоростью ω0 рад/с, вращающегося против часовой стрелки. При увеличении t (от t0 до t1) мы можем изобразить пере­менные во времени проекции вращающегося вектора на синфазной (l) и квадратурной (Q) осях. Эти декартовы оси обычно называются синфазным (l channel) и квадратурным кана­лом (Q channel), а их проекции представляют взаимно ортогональные составляющие

Рис 4.2. Векторное представление синусоиды

cиг­нала, связанные с этими каналами. В-третьих, процесс модуляции несущей можно рассматривать как систематическое возмущение вращающегося вектора (и его проекций).

Рассмотрим, например, несущую, амплитудно-модулированную синусоидой с единичной амплитудой и частотой ωm, где ωm<<ω0. Переданный сигнал имеет следующий вид.

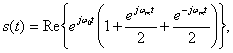(4.5)

где Re{x} — действительная часть комплексной величины {x}. На рис. 4.3 показано, что вращающийся вектор , представленный на рис. 4.2, возмущается двумя боко­выми членами — , вращающимся против часовой стрелки, и , вращающим­ся по часовой стрелке. Боковые векторы вращаются намного медленнее, чем вектор несущей волны. В результате модулированный вращающийся вектор несущей волны растет и уменьшается согласно указаниям боковых полос, но частота его вращения остается постоянной; отсюда и название "амплитудная модуляция".

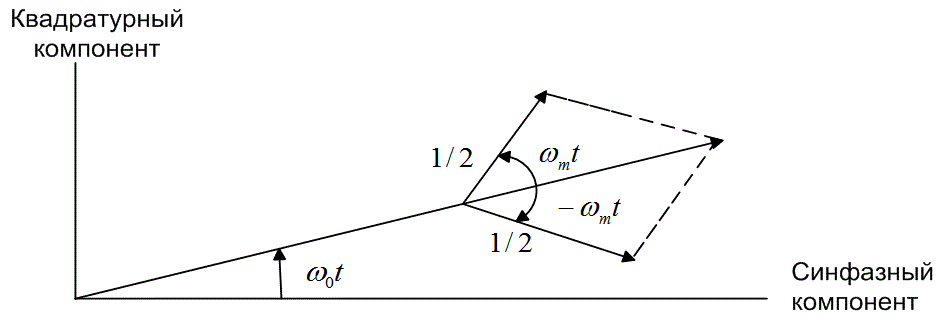
Рис 4.3. Амплитудная модуляция

Еще один пример, иллюстрирующий полезность векторного представления, — это частотная модуляция (frequency modulation — FM) несущей похожей синусоидой с частотой вращения ωm рад/с. Аналитическое представление узкополосной частотной модуляции (narrowband FM — NFM) подобно представлению амплитудной модуляции и описывается выражением:

(4.6)

где β — коэффициент модуляции [1]. На рис. 4.4 показано, что, как и в предыдущем случае, вектор несущей волны возмущается двумя боковыми векторами. Но поскольку один из них, как указано в формуле (4.6), имеет знак "минус", симметрия боковых векторов, вращающихся по часовой стрелке и против нее, отличается от имеющейся в случае амплитудной модуляции. При модуляции AM симметрия приводит к увеличе­нию и уменьшению вектора несущей волны со временем. В случае модуляции NFM симметрия боковых векторов (на 90° отличающаяся от симметрии AM) приводит к ускорению и замедлению вращения вектора согласно указаниям боковых полос, при этом амплитуда остается неизменной; отсюда название "частотная модуляция".

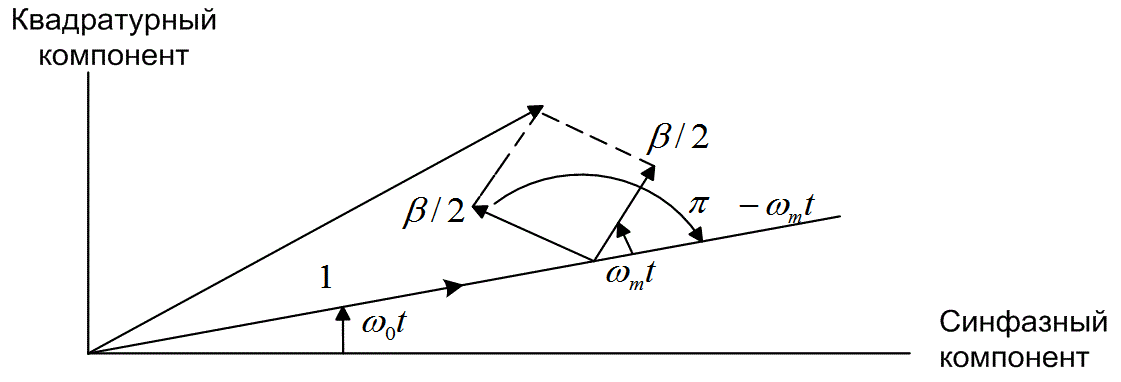
Рис 4.4. Узкополосная частотная модуляция

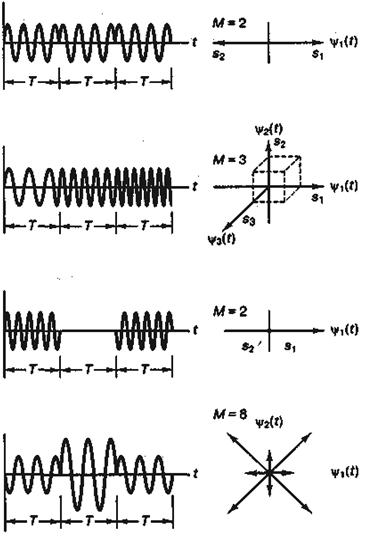
На рис. 4.5 изображены наиболее распространенные форматы цифровой модуляции: PSK, FSK, ASK и смешанная комбинация ASK и PSK (обозначаемая как ASK/PSK, или АРК). В первом столбце указаны аналитические выражения, во втором — временная диаграмма, а в третьем — векторная диаграмма. В общем случае M-арной передачи сигналов устройство обработки получает k исходных битов (или канальных битов, если используется кодирование) в каждый момент времени и ука­зывает модулятору произвести один из М = 2^k возможных сигналов. Частным случаем M-уровневой модуляции является бинарная с k=1.

На рис. 4.2 несущая волна представлялась как вектор, вращающийся на плоскости со скоростью, равной частоте несущей, ω0 рад/с. На рис. 4.5 векторная схема каждой цифровой модуляций представляет совокупность информационных сигналов (векторов или точек пространства сигналов) без указания времени. Другими словами, на рис. 4.5 не отображено вращение немодулированного сигнала с постоянной скоро­стью, а представлено только взаимное расположение векторов-носителей информа­ции. Стоит обратить внимание, что в примерах на рис. 4.5 значения размера множе­ства M отличаются.

Аналитическое представление Сигнал Вектор

а) PSK б) FSK в) ASK г) ASK/PSK (APK)

Рис. 4.5. Виды цифровых модуляций: a) PSK; б) FSK; в) ASK; г) ASK/PSK (АРК)

4.2.2. Фазовая манипуляция

Фазовая манипуляция (phase shift keying — PSK) была разработана в начале развития про­граммы исследования дальнего космоса; сейчас схема PSK широко используется в ком­мерческих и военных системах связи. Сигнал в модуляции PSK имеет следующий вид.

(4.7)

Здесь фазовый член может принимать M дискретных значений, обычно опреде­ляемых следующим образом.

На рис. 4.5, а приведен пример двоичной (M = 2) фазовой манипуляции (binary PSK — BPSK). Параметр Е — это энергия символа, Т — время передачи символа, . Работа схемы модуляции заключается в смещении фазы модулируемого сигнала s,(r) на одно из двух значений, нуль или π (180°). Типичный вид сигнала в модуляции BPSK приведен на рис. 4.5, а, где явно видны характерные резкие изменения фазы при переходе между символами; если модулируемый поток данных состоит из чере­дующихся нулей и единиц, такие резкие изменения будут происходить при каждом переходе. Модулированный сигнал можно представить как вектор на графике в полярной системе координат; длина вектора соответствует амплитуде сигнала, а его ориентация в общем M-арном случае — фазе сигнала относительно других М - 1 сигналов набора. При модуляции BPSK векторное представление дает два противофазных (180°) вектора. Наборы сигналов, которые могут быть представлены подобными про­тивофазными векторами, называются антиподными.

4.2.3. Частотная манипуляция

Общее аналитическое выражение для сигнала в частотной манипуляции (frequency shift keying — FSK) имеет следующий вид.

(4.8)

Здесь частота ω0 может принимать М дискретных значений, а фаза φ является про­извольной константой. Схематическое изображение сигнала в модуляции FSK дано на рис. 4.5, б, где можно наблюдать типичное изменение частоты (тона) в моменты переходов между символами. Такое поведение характерно только для частного слу­чая FSK, называемого частотной манипуляцией без разрыва фазы (continuous-phase FSK — CPFSK); она описана в разделе 9.8. В общем случае многочастотной мани­пуляции (multiple frequency shift keying — MFSK) переход к другому тону может быть довольно резким, поскольку непрерывность фазы здесь не обязательна. В при­веденном примере М = 3, что соответствует такому же числу типов сигналов (троичной передаче); отметим, что значение М = 3 было выбрано исключительно для демонстрации на рисунке взаимно перпендикулярных осей. На практике М обычно является ненулевой степенью двойки (2, 4, 8, 16, ...), что довольно сложно изобразить графически. Множество сигналов описывается в декартовой системе ко­ординат, где каждая координатная ось представляет синусоиду определенной часто­ты. Как говорилось ранее, множества сигналов, которые описываются подобными взаимно перпендикулярными векторами, называются ортогональными (orthogonal). Не все схемы FSK относятся к ортогональным. Чтобы множество сигналов было ор­тогональным, оно должно удовлетворять критерию, выраженному в формуле (3.69). Этот критерий навязывает определенные условия на взаимное размещение тонов множества. Расстояние по частоте между тонами, необходимое для удовлетворения требования ортогональности.

4.2.4. Амплитудная манипуляция

Сигнал в амплитудной манипуляции (amplitude shift keying — ASK), изображенной на рис. 4.5, в, описывается выражением (4.9)

где амплитудный член может принимать М дискретных значений, а фазо­вый член φ — это произвольная константа. На рис. 4.5, в М выбрано равным 2, что соответствует двум типам сигналов. Изображенный на рисунке сигнал в модуляции ASK может соответствовать радиопередаче с использованием двух сигналов, амплиту­ды которых равны 0 и . В векторном представлении использованы те же фазово-амплитудные полярные координаты, что и в примере для модуляции PSK. Правда, в данном случае мы видим один вектор, соответствующий максимальной амплитуде с точкой в начале координат, и второй, соответствующий нулевой амплитуде. Передача сигналов в двухуровневой модуляции ASK — это одна из первых форм цифровой модуляции, изобретенных в начале столетия для беспроводной телеграфии. В настоящее время простая схема ASK в системах цифровой связи уже не используется.

4.2.5. Амплитудно-фазовая манипуляция

Амплитудно-фазовая манипуляция (amplitude phase keying — АРК) — это комбинация схем ASK и PSK. Сигнал в модуляции АРК изображен на рис. 4.5, г и выражается как

(4.10)

с индексированием амплитудного и фазового членов. На рис. 4.5, г можно видеть харак­терные одновременные (в моменты перехода между символами) изменения фазы и ампли­туды сигнала в модуляции АРК. В приведенном примере М=8, что соответствует 8 сигна­лам (восьмеричной передаче). Возможный набор из восьми векторов сигналов изображен на графике в координатах "фаза-амплитуда". Четыре показанных вектора имеют одну ам­плитуду, еще четыре — другую. Векторы ориентированы так, что угол между двумя бли­жайшими векторами составляет 45°. Если в двухмерном пространстве сигналов между М сигналами набора угол прямой, схема называется квадратурной амплитудной модуляцией (quadrature amplitude modulation — QAM); примеры QAM рассмотрены в главе 9.

Векторные представления модуляций, изображенные на рис. 4.5 (за исключением слу­чая FSK), изображены графиками, полярные координаты которых представляют амплитуду и фазу сигнала. Схема FSK подразумевает ортогональную передачу (см. раздел 4.5.4) и описывается в декартовой системе координат, где каждая ось представляет тон частоты (), совокупность которых формирует М-значный набор ортогональных тонов.

4.2.6. Амплитуда сигнала

Амплитуды сигналов, представленные в формулах (4.7)-(4.10), имеют одинаковый вид для всех форматов модуляции. Выведем это. Сигнал описывается формулой

(4.11)

где А — максимальная амплитуда сигнала. Поскольку максимальное значение в V2 раза больше его среднеквадратического (root-mean-square — rms) значения, можем за­писать следующее.

Предполагается, что сигнал выражен через колебания тока или напряжения, так что

представляет среднюю мощность Р (нормированную на 1 Ом). Значит, можем записать следующее.

(4.12)

Заменяя Р (единицы измерения — ватт) на Е (джоули)/Т (секунды), получаем следующее.

(4.13)

Итак, амплитуду сигнала можно записать либо в общем виде, как в формуле (4.11), либо через , как в формуле (4.13). Поскольку ключевой параметр при опреде­лении вероятности ошибки в процессе обнаружения — это энергия принятого сигнала, зачастую удобнее использовать запись в форме (4.13), так как в этом случае вероят­ность ошибки ре можно получить сразу как функцию энергии сигнала.

4.3. Обнаружение сигнала в гауссовом шуме

          Полосовая модель процесса обнаружения, рассмотренная в данной главе, практически идентична узкополосной модели, представленной в главе 3. Дело в том, что принятый полосовой сигнал вначале преобразовывается в узкополосный, после чего наступает этап окончательного обнаружения. Для линейных систем математика процесса обна­ружения не зависит от смещения частоты. Фактически теорему эквивалентности можно определить следующим образом: выполнение полосовой линейной обработки сигнала с последующим наложением сигнала (превращением полосового сигнала в узкополосный) дает те же результаты, что и наложение сигнала с последующей узко­полосной линейной обработкой сигнала. Термин "наложение сигнала" (heterodyning) обозначает преобразование частоты или процесс смешивания, вызывающий смещение спектра сигнала. Как следствие теоремы эквивалентности, любая линейная модель обработки сигналов может использоваться для узкополосных сигналов (что предпоч­тительнее с точки зрения простоты) с теми же результатами, что и для полосовых сигналов. Это означает, что производительность большинства цифровых систем связи часто можно описать и проанализировать, считая канал передачи узкополосным.

4.3.1. Области решений

Предположим, что двухмерное пространство сигналов, изображенное на рис. 4.6, — это геометрическое место точек, возмущенных шумом двоичных векторов-прототипов . Вектор шума n — это случайный вектор с нулевым средним; следова­тельно, вектор принятого сигнала г — это случайный вектор со средним значением s, или s2. Задачей детектора после получения г является принятие решения относитель­но классификации сигнала, имеющего минимальную вероятность ошибки Pв, хотя возможны и другие стратегии принятия решения [2]. Для случая М = 2 с равновероят­ными сигналами s1 и s2 и при шуме AWGN (additive white Gaussian noise — аддитив­ный белый гауссов шум) использование при принятии решения критерия минимума ошибки равносильно такому выбору класса сигнала, чтобы расстояние было минимальным, где ||х|| — норма или абсолютная величина вектора х. Последнее правило часто формулируется в терминах областей решений. Обратимся к рис. 4.6 и рассмотрим формирование областей решений. Итак, вначале необходимо соединить концы векторов-прототипов s1 и s2. Затем через середину полученного отрезка прово­дится плоскость, перпендикулярная к нему. Отметим, что поскольку амплитуды сиг­налов s1 и s2 равны, эта плоскость проходит через начало координат и является бис­сектрисой угла, образованного векторами-прототипами. Эта биссекторная плоскость, изображенная на рис. 4.6 для случая М = 2, является геометрическим местом точек, равноудаленных от векторов s1 и s2; следовательно, она является границей между об­ластью решений 1 и областью решений 2. Правило принятия решения, используемое детектором, формулируется в терминах областей решений следующим образом: если сигнал расположен в области 1 — отнести принятый сигнал к s1; если в области 2 — выбрать сигнал s2. Если угол θ (рис. 4.6) равен 180°, набор сигналов s1 и s2 описывает модуляцию BPSK. Впрочем, для иллюстрации идеи области решений вообще угол θ на рисунке был заведомо выбран меньшим 180°.

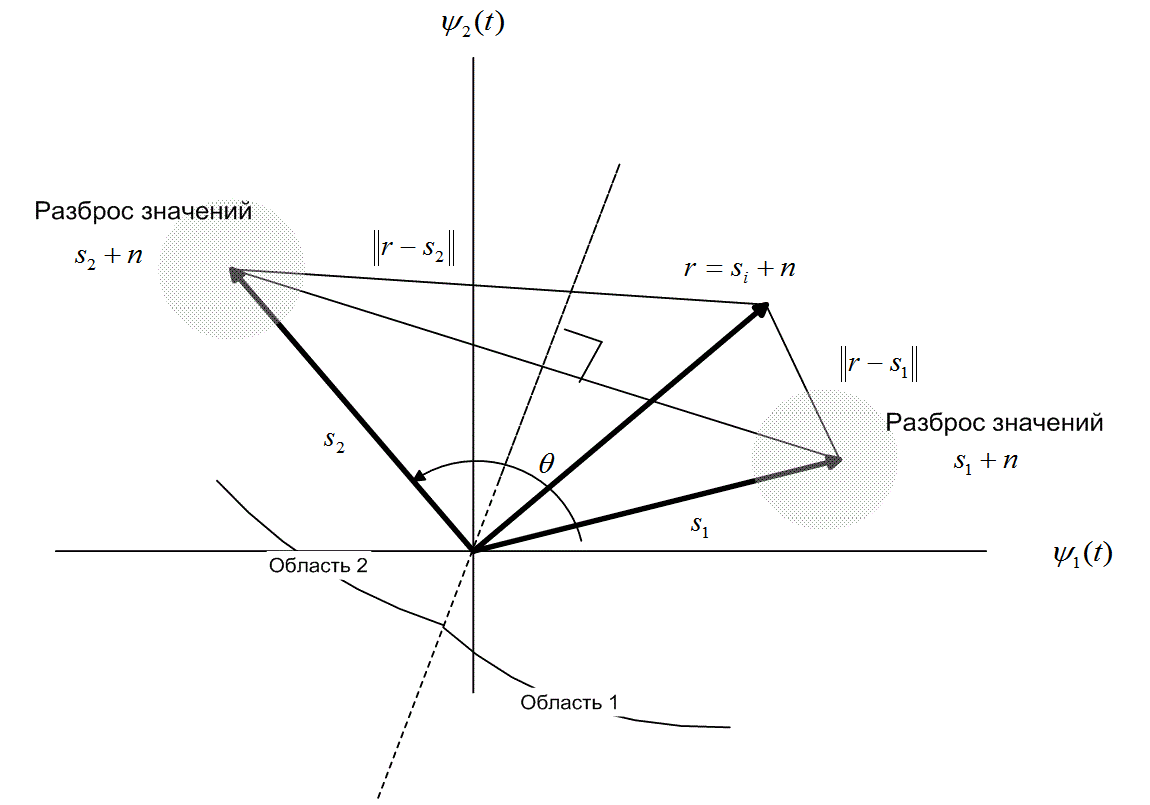
Рис. 4.6. Двухмерное пространство сигналов с равными по модулю произвольными векторами s1 и s2

4.3.2. Корреляционный приемник

В разделе 3.2 было рассмотрено обнаружение узкополосных двоичных сигналов в гауссовом шуме. Поскольку при обнаружении полосовых сигналов используются те же понятия, в данном разделе мы просто обобщим ключевые результаты. Основное внимание будет уделено реализации согласованного фильтра, известного как коррелятор (correlator). Помимо двоичного обнаружения будет рассмотрен бо­лее общий случай М-арного обнаружения. Предполагается, что сигнал искажается только вследствие шума AWGN. Принятый сигнал будем описывать как сумму переданного сигнала и случайного шума.

(4.14)

При наличии подобного принятого сигнала процесс обнаружения, как показано на рис. 3.1, включает два основных этапа. На первом этапе принятый сигнал r(t) усекается до одной случайной переменной z(T) или до набора случайных переменных zi(T) (i=1,...,М), формируемых на выходе демодулятора и устройства дискретиза­ции в момент времени t = Т, где Т — длительность символа. На втором этапе на основе сравнения z(T) с порогом или согласно критерию максимума zi(T) прини­мается решение относительно значения cимвола. Вообще, этап 1 можно рассмат­ривать как преобразование сигнала в точку в пространстве решений. Эту точку, представляющую собой важнейшую контрольную точку в приемнике, можно на­звать додетекторной (predetection). Когда мы говорим о мощности принятого сиг­нала, мощности принятых шумов или отношении еь/nq, все эти величины всегда рассматриваются относительно додетекторной точки. Иногда такие параметры оп­ределяются относительно входа приемника или принимающей антенны. Но в по­добных случаях всегда подразумевается, что между выбранной и додетекторной точками не происходит снижения отношения сигнал/шум, или Eb/N0. В каждый момент передачи символа сигнал, доступный в додетекторной точке, является вы­боркой узкополосного импульса. На данный момент битового значения у нас еще нет. Стоит ли удивляться, что отношение энергии бита к N0 определено там, где еще не существует бита? В действительности, нет, поскольку данная точка явля­ется удобной контрольной точкой, где узкополосный импульс — даже до приня­тия решения на битовом уровне — может давать эффективное представление би­тов. Этап 2 можно рассматривать как определение того, в какой области решений расположена данная точка. Для оптимизации детектора (в смысле минимизации вероятности ошибки) необходимо оптимизировать преобразование сигнала в слу­чайную переменную с использованием согласованных фильтров или корреляторов на этапе 1 и оптимизировать критерий принятия решения на этапе 2.

В разделах 3.2.2 и 3.2.3 показывалось, что согласованный фильтр обеспечивает максимальное отношение сигнал/шум на выходе фильтра в момент t = Т. Как одна из реализаций согласованного фильтра описывался коррелятор. Теперь мы можем опре­делить корреляционный приемник (correlation receiver), состоящий, как показано на рис. 4.7, а, из М корреляторов, выполняющих преобразование принятого сигнала r(t) в последовательность М чисел или выходов коррелятора, zi(T) (i=1,...,М). Каждый вы­ход коррелятора описывается следующим интегралом произведения или корреляцией с принятым сигналом.

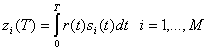(4.15)

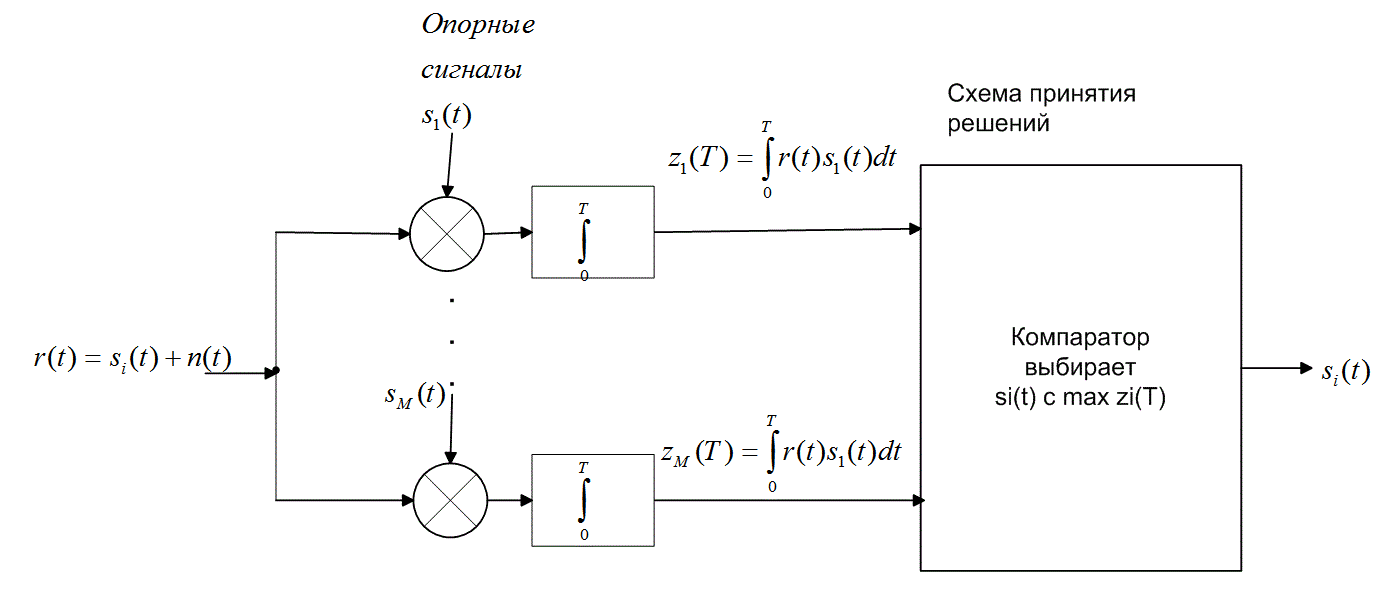
а)

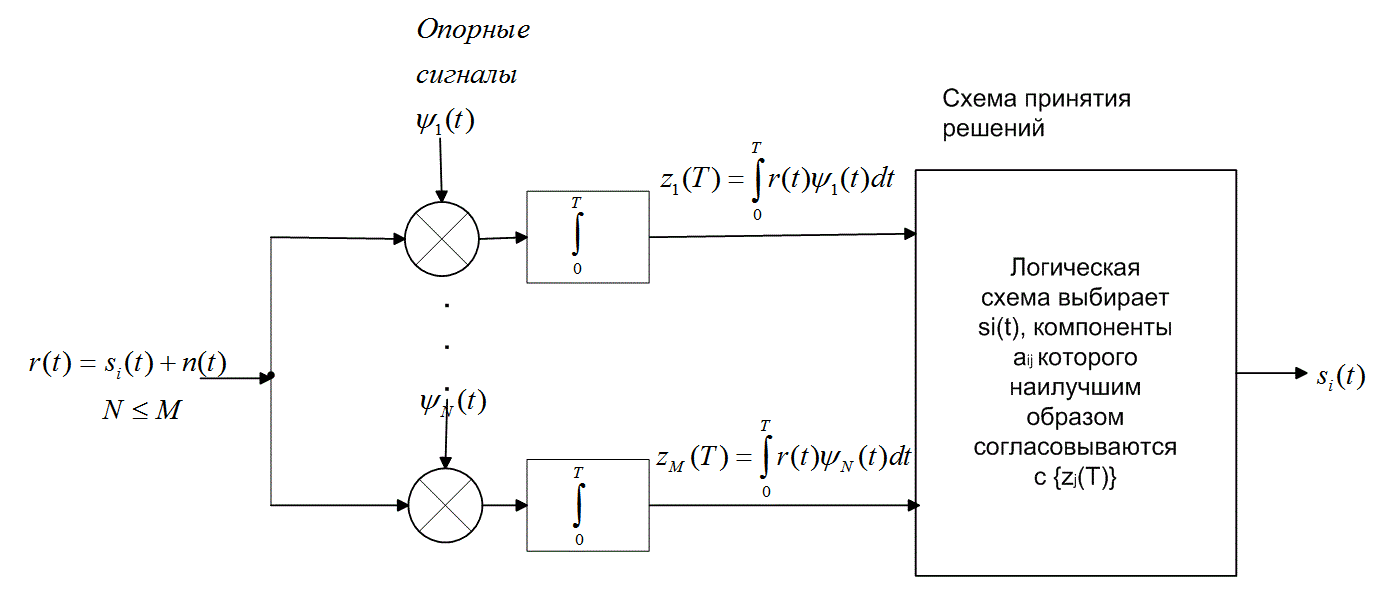
б)

Рис. 4.7. Корреляционный приемник: а) корреляционный приемник с опорными сигналами ; б) корреляционный приемник с опорными сигналами

Глагол "коррелировать" означает "совпадать", "согласовываться". Корреляторы пытаются найти соответствие принятого сигнала r(t) с каждым возможным сигналом-прототипом si(t), известным приемнику априори. Разумное правило принятия реше­ния звучит так: выбирать сигнал si(t), лучше всего согласующийся, (или имеющий наи­большую корреляцию) с r(t). Другими словами, правило принятия решения выглядит следующим образом.

Выбрать сигнал si(t), индекс которого

Соответствует максимальной zi(T) (4.16)

Следуя формуле (3.10), любой набор сигналов можно выразить через определенный набор базисных функций . Таким образом, группу из М корреляторов, изображенную на рис. 4.7, а, можно заменить группой из N корреляторов, показанной на рис. 4.7, б, где в качестве опорных сигналов используется на­бор базисных функций . Для принятия решения с помощью указанных корреляторов необходима логическая схема выбора сигнала si(t) Выбор производится на основе опреде­ления наилучшего согласования коэффициентов aij, фигурирующих в формуле (3.10), с на­бором выходов {zj(T)}. Если набор сигналов-прототипов {s,{t)} формирует ортогональное множество, реализация приемника, показанная на рис. 4.7, а, идентична реализации, по­казанной на рис. 4.7, б (могут отличаться масштабом). Если же {si(t)} не является ортого­нальным множеством, приемник (рис. 4.7, б), использующий N корреляторов с опорными сигналами вместо М, представляет более рентабельную реализацию. В разделе 4.4.3 мы рассмотрим применение подобного устройства для обнаружения сигнала в модуляции MPSK (multiple phase shift keying — многофазная манипуляция).

В случае двоичного обнаружения корреляционный приемник, как показано на рис. 4.8, а, можно построить как согласованный фильтр или интегратор произведений с опорным сигналом, равным разности двоичных сигналов-прототипов . Вы­ход коррелятора z(T) используется непосредственно в процессе принятия решения.

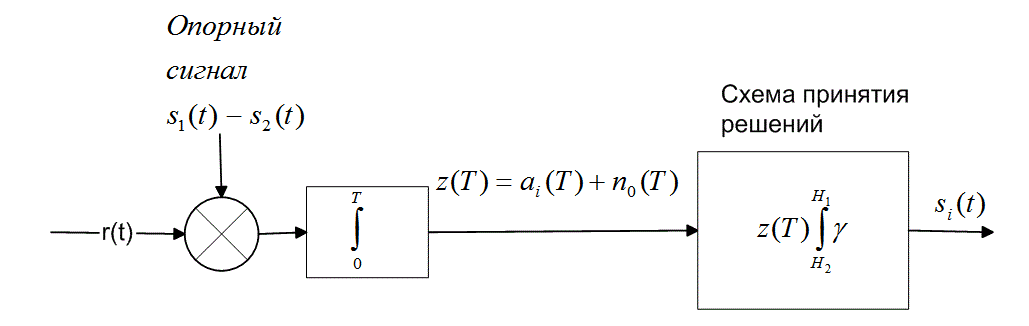
а)

б)

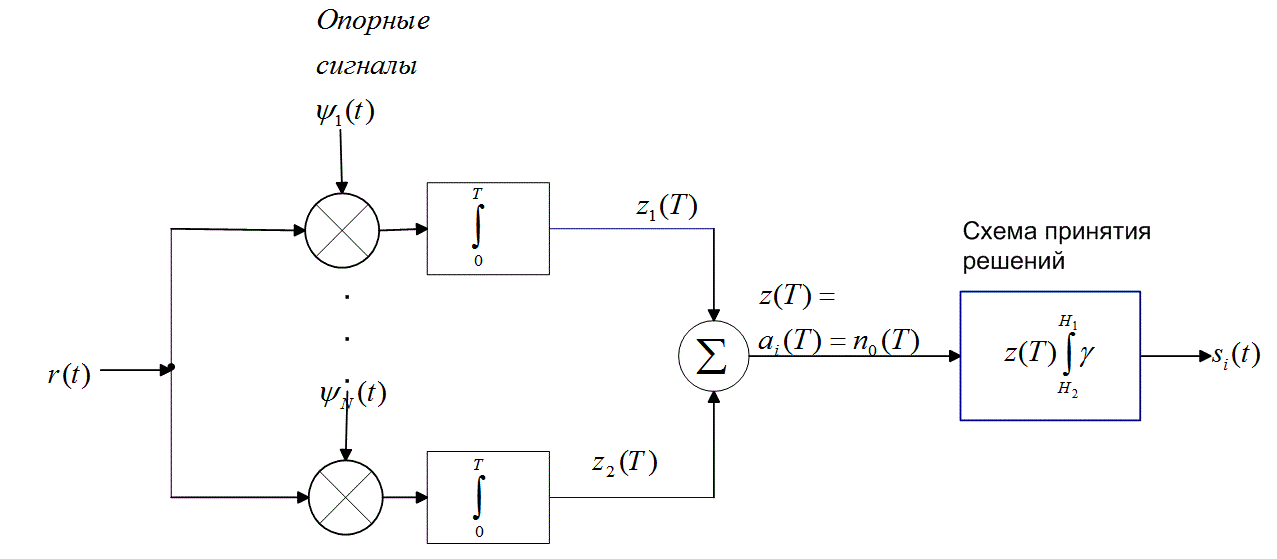
Рис. 4.8. Двоичный корреляционный приемник: а) использование одного коррелятора; б) применение двух корреляторов

При двоичном обнаружении корреляционный приемник можно изобразить как два согласованных фильтра или интегратора произведений, один из которых согласовывается с s1(t), а второй — с s2(t) (рис. 4.8, б). На этапе принятия решения теперь может использо­ваться правило, приведенное в формуле (6.16), или же из выхода одного коррелятора мож­но вычесть выход другого и на этапе принятия решения использовать разность

, (4.17)

как показано на рис. 4.8, б. Здесь z(T), называемое тестовой статистикой (test statistic), подается в схему принятия решения, как и в случае только одного корреля­тора. В отсутствие шума на выходе мы получаем z(7) = аi(T), где ai(T) — сигнальный компонент. Входной шум и(7) при этом является случайным гауссовым процессом. Поскольку коррелятор — это линейное устройство, выходной шум является случайным гауссовым процессом [2]. Таким образом, можно записать выражение с выхода корре­лятора в момент взятия выборки t = Т:

где п0(Т) — компонент шума. Для сокращения записи мы иногда будем выражать z(t) как а, + n0. Компонент шума п0 — это гауссова случайная переменная с нулевым сред­ним; следовательно, z(T) — это гауссова случайная переменная со средним a1 или а2в зависимости от того, была передана двоичная единица или двоичный нуль.

4.3.2.1. Порог двоичного решения

На рис. 4.9 для случайной переменной z(T) показаны две плотности условных вероятностей — и — со средними значениями а1и а2. Эти функции, име­нуемые правдоподобием s1 и правдоподобием s2, были представлены в разделе 3.1.2. Приведем их повторно.

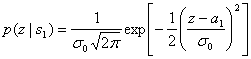(4.18,а)

и

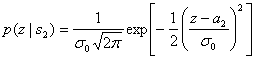(4.18,б)

Здесь — дисперсия шума. На рис. 4.9 правое правдоподобие иллюстрирует вероятностное распределение сигналов на выходе детектора z(T) при переданном сигнале s1. Подобным образом левое правдоподобие p(z|s2) демонстрирует вероятностное распределение сигналов на выходе детектор z(T) при переданном сигнале s2. Абсцисса z(T) представляет полный диапазон возможных значений выборок на выходе корреляционного приемника, показанного на рис. 4.8.

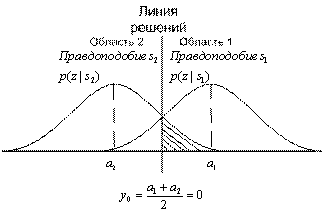
Рис. 4.9. Плотности условных вероятностей и

При рассмотрении задачи оптимизации порога двоичного решения относительно принадлежности принятого сигнала к одной из двух областей, в разделе 3.2.1 было показано, что критерий минимума ошибки для равновероятных двоичных сигналов, искаженных гауссовым шумом, можно сформулировать следующим образом.

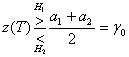(4.19)

Здесь — сигнальный компонент z(Т) при передаче s1(t), а — сигнальный компонент z(T) при передаче s2(t). Порог γ0, равный (а1 + а2)/2 — это оптимальный порог для миними­зации вероятности принятия неверного решения при равновероятных сигналах и симмет­ричных правдоподобиях. Правило принятия решения, приведенное в формуле (4.19), ука­зывает, что гипотеза H1 (решение, что переданный сигнал — это s1(t)) выбирается при z(T)> γ0, а гипотеза Н2(решение, что переданный сигнал — это s2(t)) — при z(T) < γ0. Если z(T) = γ, решение может быть любым. При равновероятных антиподных сигналах с равны­ми энергиями, где s1(t)= -s2(t) и а1 = -а2, оптимальное правило принятия решения прини­мает следующий вид.

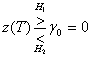(4.20,а)

4.4. Когерентное обнаружение

4.4.1. Когерентное обнаружение сигналов PSK

На рис. 4.7 показан детектор, который может использоваться для когерентного обна­ружения любого цифрового сигнала. Подобный корреляционный детектор часто на­зывается детектором, работающим по критерию максимального правдоподобия (maximum likelihood detector). Рассмотрим следующую бинарную модуляцию PSK (BPSK). Пусть

(4.21,а)

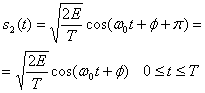(4.21,б)

n(t) — случайный белый гауссов процесс с нулевым средним.

Здесь фазовый член φ — произвольная константа, которую мы для удобства положим равной нулю. Параметр Е — это энергия сигнала, приходящаяся на символ, а Т — дли­тельность символа. Для данного антиподного случая требуется единственная базисная функция. Используя формулы (3.10) и (3.11) и предполагая пространство ортонормированным (т.е. Kj= 1), базисную функцию можно выразить следующим образом.

(4.22)

Следовательно, переданный сигнал si(t) можно выразить через функцию и коэф­фициенты .

(4.23,а)

(4.23,б)

(4.23,в)

Предположим, что был передан сигнал s1(t). Тогда математические ожидания на выхо­дах интеграторов произведений, изображенных на рис. 4.7, б, при опорном сигнале имеют следующий вид.

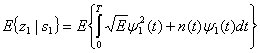(4.24,а)

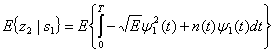(4.24,б)

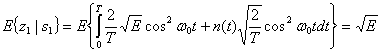(4.25,а)

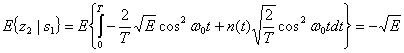(4.25,б)

Здесь обозначает среднее по ансамблю, так называемое математическое ожида­ние (expected value). В уравнении (4.25) E{n(t)} = 0. На этапе принятия решения, путем определения местоположения переданного сигнала в сигнальном пространстве, необходимо определить значение данного сигнала. В приведенном примере, где в качестве базисной функции была взята , значения равны .Сигналы-прототипы аналогичны опорным сигналам , с точностью до нормирующего множителя. На этапе принятия решения выбирается сигнал с боль­шим значением zi(T). Следовательно, в приведенном выше примере принятый сигнал определен как s1(t). Вероятность ошибки при подобном когерентном обнаружении сигналов BPSK рассмотрена в разделе 4.7.1.

4.4.2. Цифровой согласованный фильтр

В разделе 3.2.2 рассматривалась основная особенность согласованного фильтра — то, что его импульсная характеристика представляет собой запаздывающую версию зер­кального отображения (поворота относительно оси t = 0) входного сигнала. Таким об­разом, если сигнал равен s(t), его зеркальное отображение имеет вид s(-t), а зеркальное отображение, запаздывающее на Т секунд, имеет вид s(T-t). Следовательно, импульсная характеристика h(t), соответствующая сигналу s(t), будет равна следующему.

(4.26)

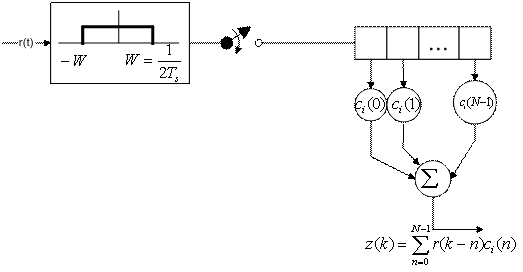
На рис. 4.7 и 4.8 представлена основная функция коррелятора — интегрирование произведения принятого зашумленного сигнала с каждым опорным сигналом и определение наилучшего соответствия. Схемы, показанные на этих рисунках, подразуме­вают использование аналоговой аппаратуры (умножителей и интеграторов) и непре­рывных сигналов. На них не отражена возможность реализации коррелятора или со­гласованного фильтра (matched filter — MF) с использованием цифровых технологий и дискретных сигналов. Пример подобной реализации приведен на рис. 4.10, где по­казан согласованный фильтр, использующий цифровую аппаратуру. Входной сигнал r(t) состоит из сигнала-прототипа s,(t) и шума n(i); ширина полосы сигнала W= 1/2T, где Т — длительность передачи символа. Таким образом, минимальная частота дис­кретизации по Найквисту равна fs = 2W= 1/T, а время взятия выборки (Ts) должно быть не больше времени передачи символа. Другими словами, на символ должно прихо­диться не менее одной выборки. В реальных системах подобная дискретизация произ­водится с частотой, в 4 или более раз превышающей минимальную частоту Найквиста. Платой за это является не увеличение полосы передачи, а увеличение быстродей­ствия процессора. В моменты t = kTs выборки (как показано на рис. 4.10, а) сдвигаются в регистре, так что более ранние из них располагаются правее. При дис­кретизации (взятии выборки) полученного сигнала непрерывное время t заменяется дискретным kTs или просто k, что дает право использовать дискретную запись.

Здесь индекс i определяет символ из М-арного набора (в нашем случае — двоичного), a k — дискретное время. На рис. 4.10 согласованный фильтр аппроксимируется реги­стром сдвига с весовыми коэффициентами с/(п), где п=0,...,N-1 — временной ин­декс весовых коэффициентов и разрядов регистра. В приведенном примере число раз­рядов регистра и количество выборок на символ равны 4. Итак, суммирование, пока­занное на рисунке, происходит в моменты времени от n = 0 до n = 3. Из расположения сумматора на схеме понятно что решение относительно значения принятого сигнала принимается после заполнения регистра 4 выборками. Отметим, что для простоты в примере на рис. 4.10, б выборки si(k) могут принимать только три значения (0, ±1). В реальных системах каждая выборка (и весовой коэффициент) — это 6-10 бит. Множе­ству весовых коэффициентов фильтра {ci(n)} соответствует импульсная характеристика фильтра; согласование весовых коэффициентов с выборками сигнала производится согласно дискретному варианту уравнения (4.26).

(4.27)

Использование дискретной формы интеграла свертки из уравнения (А.44,6) позволяет записать выражение с выхода коррелятора в момент времени, соответствующий k-й. выборке.

 

(4.28)

а)

 

б)

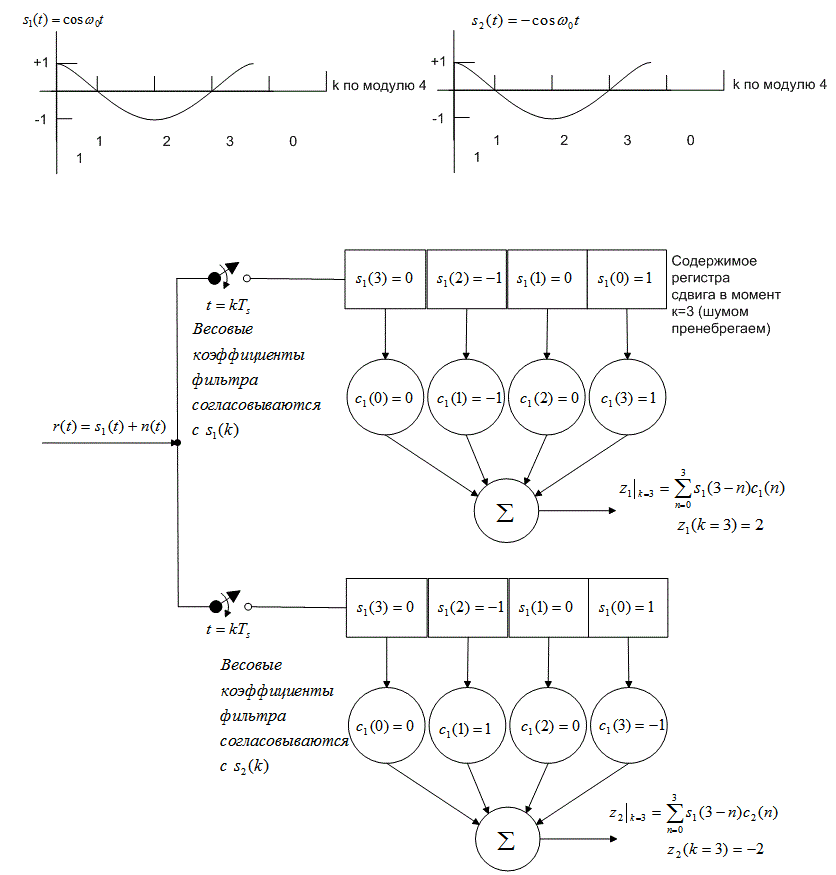
Рис. 4.10. Цифровой согласованный фильтр: а) дискретный согласованный фильтр; б) пример обнаружения с использованием дискретного согласованного фильтра (шумом пренебрегаем)

Здесь х по модулю у — это остаток деления х на у, индекс k — время принятия выбо­рок и выхода фильтра, an — фиктивная переменная времени. В формуле (4.28) выра­жение r(k-n) содержит п, которое можно рассматривать как "возраст" выборки (как давно она находится в фильтре). В выражении сi(п) л удобно рассматривать как адрес весового коэффициента. Предполагается, что система синхронизирована и упорядоче­ние символов во времени известно. Также предполагается, что шум имеет нулевое среднее, так что математическое ожидание принятой выборки равно следующему.

Следовательно, при передаче si(t) математическое ожидание выхода согласованного фильтра равно следующему.

(4.29)

На рис. 4.10, б, где сигналы-прототипы изображены как функции времени, видим, что крайняя слева выборка (амплитуда, равная +1) графика s1(t) представляет выборку в момент времени k = 0. Предполагая, что передан был сигнал s1(t) и для упрощения записи мы пренебрегли шумом, можем записать принятую выборку r(k) как s1(k). Выборки заполняют разряды согласованного фильтра, и в конце каждого периода передачи символа в крайнем правом разряде каждого регистра расположена выборка k=0. Отметим, что в формулах (4.28) и (4.29) временные индексы п эталонных весовых ко­эффициентов расположены в порядке, обратном к временному индексу k - п выборок, что является ключевой особенностью интеграла свертки. То, что наиболее ранняя вы­борка теперь соответствует крайнему справа весовому коэффициенту, обеспечивает значащую корреляцию. Даже если действия согласованного фильтра мы математиче­ски опишем как свертку сигнала с импульсной характеристикой фильтра, конечный результат будет корреляцией сигнала с копией самого себя. По этой причине корреля­тор можно реализовать как согласованный фильтр.

На рис. 4.10, б обнаружение, происходящее после выхода сигнала с согласованного фильтра, осуществляется обычным образом. Для принятия двоичного решения выхо­ды z/(£) изучаются при каждом значении k=N-l, соответствующем концу символа. При условии передачи st(t) и пренебрежении шумом, уравнения (4.27)-(4.29) можно объединить и записать выходы коррелятора в моменты времени k =

= N -1=3.

(4.30,а)

(4.30,б)

Поскольку z1 (k = 3) больше z2(k = 3), детектор принимает решение, что передан был символ s1(t).

Может возникнуть вопрос: чем согласованный фильтр на рис. 4.10, б отличается от коррелятора на рис. 4.8. В случае согласованного фильтра в ответ на каждую новую вы­борку на входе появляется новое значение на выходе; следовательно, выход представляет собой временной ряд, такой как на рис. 3.7, б (последовательность возрастающих поло­жительных и отрицательных корреляций с входной синусоидой). Подобную последова­тельность на выходе согласованного фильтра можно получить при использовании не­скольких корреляторов, работающих на разных начальных точках входящего временного ряда. Отметим, что за время передачи символа на выходе коррелятора получаем макси­мальное значение сигнала в момент времени Т (см. рис. 3.7, б). Если синхронизировать согласованный фильтр и коррелятор, их выходы в конце периода передачи символа будут идентичными. Важным отличием между согласованным фильтром и коррелятором является то, что поскольку на выходе коррелятора получаем одно значение на символ, он должен использовать дополнительную информацию, например, относительно момен­тов начала и завершения интегрирования произведения. При наличии ошибок синхро­низации дискретный сигнал, подаваемый с коррелятора на детектор, может быть сильно искажен. С другой стороны, поскольку на выходе согласованного фильтра получаем временной ряд выходных значений (отражающих смещенные во времени входящие выбор­ки, умноженные на фиксированные весовые коэффициенты), использование дополни­тельной схемы позволяет определить моменты, наиболее подходящие для дискретизации выхода согласованного фильтра.

Пример 4.1. Цифровой согласованный фильтр

Рассмотрим набор сигналов

где k =0,1,2,3.

Опишите, как цифровой согласованный фильтр (рис. 4.10) может использоваться для обна­ружения принятого сигнала, скажем s1(t), при отсутствии шума.

Решение

Вначале сигнал s1(i) преобразуется в набор выборок . Приемник цифрового согласо­ванного фильтра, как показано на рис. 4.10, б, представляет собой две ветви. Верхняя ветвь состоит из регистра сдвига и коэффициентов, согласовывающихся с точками дискретизации . Подобным образом нижняя ветвь состоит из регистра сдвига и коэффициентов, со­гласовывающихся с точками дискретизации . В четырех равномерно расположенных точках выборки (k = 0, 1,2, 3) сигналы имеют следующие значения.

Коэффициенты сi(n) представляют запаздывающий зеркальный поворот сигнала, с которым согласовывается фильтр. Следовательно, так что можно записать .

Рассмотрим верхнюю ветвь рис. 4.10, б. В момент времени k = 0 первая выборка s1(k = 0) =0 поступает в крайний левый разряд каждого регистра. В следующий дискретный момент вре­мени k=1 вторая выборка s1(k= l)=A/4 поступает в крайний левый разряд каждого реги­стра; в то же время первая выборка сдвигается в ближайший справа разряд каждого регистра и т.д. В момент k =3 в крайний левый разряд поступает выборка s1(k = 3) = ЗА/4; к. этому моменту первая выборка сдвинута к крайнему правому разряду. Четыре выборки сигнала те­перь расположены в регистрах в зеркальном порядке по отношению к времени их создания. Таким образом, при данном расположении поступающих выборок сигнала и опорных ко­эффициентов выход сумматора естественным образом описывается операцией свертки и максимизирует корреляцию в соответствующей ветви.

4.4.3. Когерентное обнаружение сигналов MPSK

На рис. 4.11 показан вид сигнального пространства для набора сигналов в модуляции MPSK (multiple phase-shift keying — многофазная манипуляция); на рисунке представлена четырехуровневая (М = 4) фазовая манипуляция, или двукратная фазовая манипуляция (quadriphase shift keying — QPSK). Двоичные цифры в передатчике группируются по две, и в каждом интервале передачи символов две последовательные цифры определяют, какой из четырех возможных сигналов произведет модулятор. Для типичных когерентных М-уровневых систем PSK (MPSK) сигнал si(t) можно выразить следующим образом.

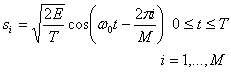(4.31)

Здесь Е — энергия, полученная сигналом за время передачи символа Т, а ω0 — несущая частота. Предполагая пространство ортонормированным и используя формулы (3.10) и (3.11), можно выбрать следующие удобные оси.

(4.32,а)

и

(4.32,б)

Здесь, как и в разделе 4.4.1, амплитуда нормирует ожидаемый выход детектора.

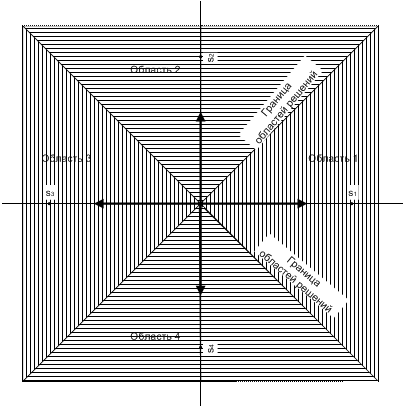
Рис. 4.11. Сигнальное пространство и области решений для системы QPSK

Запишем сигнал si(t) через выбранные ортонормированные координаты.

(4.33,а)

(4.33,б)

Отметим, что формула (4.33) выражает набор М многофазных сигналов (в общем случае не ортогональный) всего через два ортогональных несущих компонента. Случай М = 4 (QPSK) является уникальным среди множества сигналов MPSK в том смысле, что сигналы QPSK представляются комбинацией антиподных и ортогональных членов. Границы областей решений разбивают сигнальное пространство на M=4 области; процедура разбития подобна описанной в разделе 4.3.1 и изображенной на рис. 4.6 для М = 2. Правило принятия решения для детектора (рис. 4.11) звучит следующим образом: если вектор принятого сигнала попадает в область 1 — отнести его к s1(t); если вектор принятого сигнала попадает в область 2 — выбрать сигнал s2(t) и т.д. Другими словами, правило принятия решения заключается в выборе i-го сигнала, если zi(T) является наибольшим из выходов корреляторов (см. рис. 4.7).

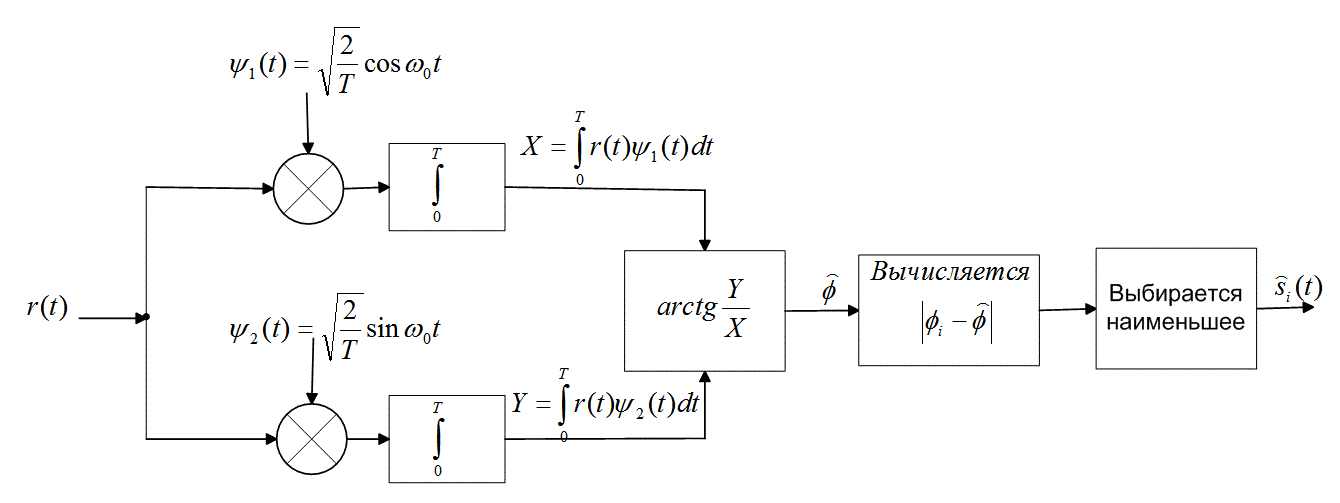
Рис. 4.12. Демодулятор сигналов MPSK

Структура коррелятора, изображенного на рис. 4.7, а, подразумевает использование для демодуляции сигналов MPSK M корреляторов произведений. Также предполагается, что для каждой из M ветвей был соответствующим образом выбран опорный сигнал (т.е. сигнал, имеющий требуемый сдвиг фаз). Стоит отметить, что на практике реализация демодулятора MPSK, согласно схеме на рис. 4.7, б, требует всего N=2 интеграторов произведений, вне зависимости от размера множества сигналов М. Такая экономия позволительна вследствие того, что, как показано в разделе 3.1.3, любой произвольный интегрируемый набор сигналов можно выразить в виде линейной комбинации ортогональных сигналов. Пример подобного демодулятора приведен на рис. 4.12. Объединив формулы (4.32) и (4.33), можно записать принятый сигнал r(t) следующим образом.

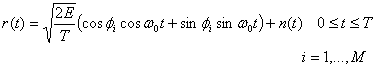(4.34)

Здесь , a n(t) — гауссов процесс шума с нулевым средним. Отметим, что на рис. 4.12 изображены только два опорных сигнала (или две базисные функции) —

для верхнего коррелятора и для нижнего. Верхний коррелятор вычисляет функцию

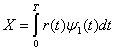(4.35)

а нижний — функцию

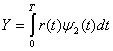(4.36)

На рис. 4.13 показано, что определение фазы принятого сигнала производится путем вычисления арктангенса Y/X, где X — синфазный, Y — квадратурный компонент принятого сигнала, а — зашумленная оценка переданной фазы . Другими словами, с верхнего коррелятора (рис. 4.12) поступает на выход X, значение синфазной проекции вектора r, а с нижнего — Y, значение квадратурной проекции вектора r, где r — векторное представление r(t). Сигналы X и Y с корреляторов поступают в блок "arctg (Y/X)". Полученное значение фазы сравнивается с каждой фазой-прототипом . Далее демодулятор выбирает фазу ближайшую к . Другими словами, демодулятор вычисляет | - | для каждого прототипа и выбирает , дающую наименьший выход.

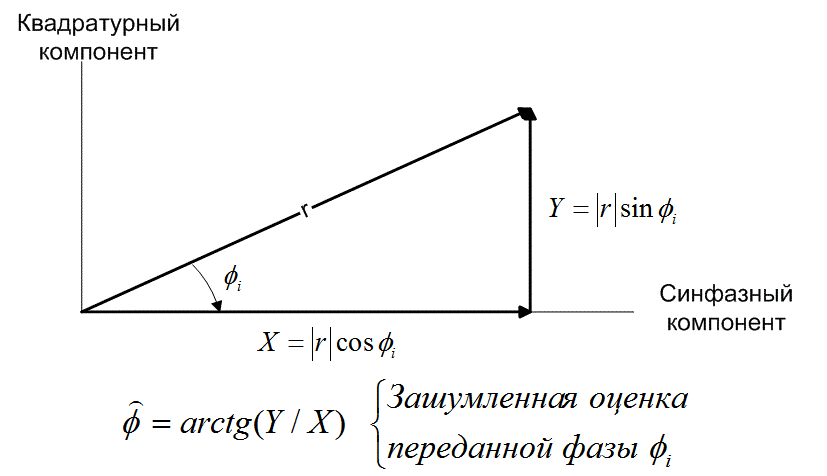
Рис. 4.13. Синфазный и квадратурный компоненты вектора принятого сигнала r

4.4.4. Когерентное обнаружение сигналов FSK

При использовании схемы FSK информация модулируется частотой несущей. Типич­ный вид набора сигналов FSK выражается формулой (4.8)

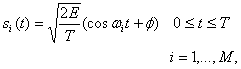
где Е — энергия, переданная сигналу в течение времени передачи символа Т; кроме того, обычно выбирается кратным . Фазовый член φ — это произвольная константа, которую можно положить равной нулю. Предполагая, что базис­ные функции формируют ортонормированное множество, можно получить более удобное выражение для .

(4.37)

Здесь, как и выше, амплитуда нормирует ожидаемый выход согласованного фильтра. Используя уравнение (3.11), можно записать следующее.

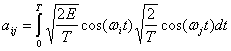(4.38)

Следовательно,

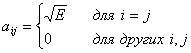(4.39)

Другими словами, i-й вектор сигнала-прототипа расположен на i-й координатной оси на расстоянии от начала координат сигнального пространства. В этой схеме, при данном числе уровней М и данной Е, расстояние между любыми двумя векторами сигналов прототипов si и sj является постоянным.

(4.40)

На рис. 4.14 показаны векторы сигналов-прототипов и области решений для троичной (М = 3) ортогональной модуляции FSK с когерентным обнаружением. Как правило, естественным выбором размера М сигнального множества является сте­пень двойки. Причина неортодоксального выбора М = 3 состоит в том, что мы жела­ем исследовать сигнальное множество, большее чем бинарное, а визуальное пред­ставление сигнального пространства лучше всего выглядит при использовании вза­имно перпендикулярных осей. Наибольшим числом перпендикулярных осей, которые можно аккуратно изобразить визуально, является 3. Как и при использова­нии модуляции PSK, сигнальное пространство разбивается на М различных облас­тей, каждая из которых содержит один вектор сигнала-прототипа; в нашем приме­ре, где области решений являются трехмерными, границы областей являются уже не линиями, а плоскостями. Оптимальное правило принятия решения состоит в следующем: определить сигнал к тому классу, индекс которого соответствует облас­ти нахождения принятого сигнала. На рис! 4.14 вектор принятого сигнала г изобра­жен в области 2. Согласно приведенному выше правилу принятия решений, детек­тор классифицирует г как сигнал s2. Поскольку шум изображается гауссовым слу­чайным вектором, существует отличная от нуля вероятность того, что вектор г даст сигнал, отличный от s2. Например, если передатчик послал сигнал s2, вектор г будет суммой сигнала и шума , а решение о выборе s2 будет справедливым; в то же время, если передатчик в действительности послал сигнал s2, вектор г будет суммой сигнала и шума , а решение относительно выбора s2 будет ошибочным. Во­просы вероятности возникновения ошибки при когерентном обнаружении сигналов в модуляции FSK подробно рассмотрены в разделе 4.7.3.

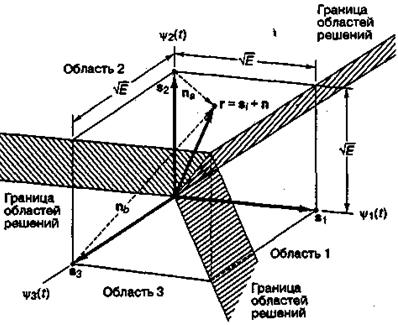
Рис. 4.14. Разбиение сигнального пространства для троичного пространства FSK

Пример 4.2. Принятая фаза как функция задержки распространения

а) Из схемы, приведенной на рис. 4.8, непонятно, откуда берутся опорные сигналы корреля­тора. Кто-то может подумать, что они известны всегда и хранятся в памяти, пока не пона­добятся. При некоторых обстоятельствах приемник действительно может, в разумных пре­делах, предсказывать некоторое ожидаемое значение амплитуды поступающего сигнала или его частоты. Но существует один параметр, который нельзя оценить без специальной по­мощи, — это фаза принятого сигнала. Наиболее популярным способом получения оценки фазы является использование схемы, называемой контурам фазовой автоподстройки часто­ты (ФАПЧ, phase-locked loop — PLL). Схема восстановления несущей захватывает прибы­вающую несущую волну (или воссоздает ее) и оценивает ее фазу. Чтобы показать, как иногда нереально предсказать фазу без использования ФАПЧ, рассмотрим канал радиосвя­зи, изображенный на рис. 4,15. Здесь мобильный пользователь расположен в точке А на расстоянии d от центральной станции, а задержка распространения сигнала равна Td. Ис­пользуя комплексную форму записи, можем описать сигнал, излучаемый передатчиком, как , Пусть частота fо равна 1 ГГц. Если пренебречь шумом, сигнал, при­нятый центральной станцией, можно записать как . Определите, на какое минимальное расстояние d (рис. 4.15) должен переместиться мобильный пользова­тель, чтобы это привело к изменению фазы принятого сигнала на 2л.

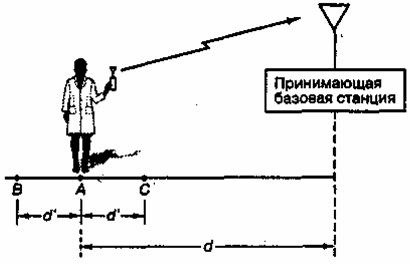
Рис. 4.15. Канал радиосвязи

б) Действительно ли нас волнует изменение фазы на 2π? Разумеется, нет, поскольку в этом случае вектор принятого сигнала будет находиться в той же точке, что и ранее, когда пользователь находился в точке А. Но зададимся вопросом, чему равно минимальное расстоя­ние, изменяющее фазу на π/2 (скажем, дающее запаздывание на π/2)? Приемник должен отнести вектор, соответствующий r(t), к той же группе, что и в п. а, но запаздывание при­водит к тому, что принятый сигнал уже имеет вид , и корреля­тор, используемый в процессе обнаружения, дает нулевой выход.

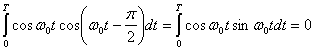
Определите минимальное расстояние перемещения пользователя, приводящее к измене­нию фазы на π/2.

Решение

а) Пусть в начальный момент времени t — 0 мобильный пользователь находится в точке А, так что вектор, принятый центральной станцией, дается выражением . Затем, после перемещения пользователя в точку В, принятый (еще сильнее запаздывающий) вектор можно записать в виде . Минимальное время задержки , соответствующее повороту вектора на 2π, равно секунд. Сле­довательно, минимальное расстояние для такого поворота (предполагая идеальное электро­магнитное распространение со скоростью света) равно следующему.

б) Используя предыдущий результат, получаем следующее расстояние для поворота вектора на π/2.

Очевидно, что даже если передатчик и приемник жестко установлены на стационарных башнях, небольшое смещение, вызванное ветром, может привести к абсолютной неопре­деленности относительно значения фазы. Если предположить, что используемая частота равна не 1 ГГц, а 10 ГГц, то минимальное расстояние изменяется с 7,5 см до 0,75 см. На практике зачастую желательно избегать приемников, использующих ФАПЧ. Вычисления, выполненные в данном примере, могут породить вопрос, как изменится вероят­ность ошибки, если в процессе обнаружения не будет использоваться информация о фа­зе? Другими словами, чем заплатит система, если обнаружение будет выполнено некогерентно? Этот и другие подобные вопросы рассматриваются в следующем разделе.

4.5. Некогерентное обнаружение

4.5.1. Обнаружение сигналов в дифференциальной модуляции PSK

Название дифференциальная фазовая манипуляция (differential phase-shift keying — DPSK) иногда требует некоторого пояснения, поскольку со словом "дифференциальный" связано два различных аспекта процесса модуляции/демодуляции: процедура кодирования и процедура обнаружения. Термин "дифференциальное кодирование" употребляется тогда, когда кодировка двоичных символов определяется не их значением (т.е. нуль или единица), а тем, совпадает ли символ с предыдущим или отличается от него. Термин "дифференциальное когерентное обнаружение" сигналов в дифференциальной модуляции PSK (именно в этом значении обычно используется название DPSK) связан со схемой обнаружения, которая зачастую относится к некогерентным схемам, поскольку не требует согласования по фазе с принятой несущей. Стоит отметить, что дифференциально кодированные сигналы PSK иногда обнаруживаются когерентно. Эта возможность будет рассмотрена в разделе 4.7.2.

В некогерентных системах не предпринимаются попытки определить действительное значение фазы поступающего сигнала. Следовательно, если переданный сигнал имеет вид

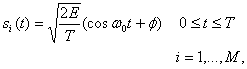
то принятый сигнал можно описать следующим образом.

 

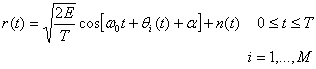(4.41)

 

Здесь α — произвольная константа, обычно предполагаемая случайной переменной, равномерно распределенной между нулем и 2π, a n(t) — процесс AWGN.

Для когерентного обнаружения используются согласованные фильтры (или их эквиваленты); для некогерентного обнаружения подобное невозможно, поскольку в этом случае выход согласованного фильтра будет зависеть от неизвестного угла а. Но если предположить, что а меняется медленно относительно интервала в два периода (2T), то разность фаз между двумя последовательными сигналами и не будет зависеть от α.

(4.42)

Основа дифференциального когерентного обнаружения сигналов в дифференциальной модуляции PSK (DPSK) состоит в следующем. В процессе демодуляции в качестве опорной фазы может применяться фаза несущей предыдущего интервала передачи символа. Ее использование требует дифференциального кодирования последовательности сообщений в передатчике, поскольку информация кодируется разностью фаз между двумя последовательными импульсами. Для передачи i-го сообщения (i= 1, 2,.... М) фаза текущего сигнала должна быть смещена на радиан относительно фазы предыдущего сигнала. Вообще, детектор вычисляет координаты поступающего сигнала путем определения его корреляции с локально генерируемыми сигналами и . Затем, как показано на рис. 4.16, детектор измеряет угол

между вектором текущего принятого сигнала и вектором предыдущего сигнала.

Вообще, схема DPSK менее эффективна, чем PSK, поскольку в первом случае, вследствие корреляции между сигналами, ошибки имеют тенденцию к распространению (на соседние времена передачи символов). Стоит помнить, что схемы PSK и DPSK отличаются тем, что в первом случае сравнивается принятый сигнал с идеальным опорным, а во втором — два зашумленных сигнала. Отметим, что модуляция DPSK дает вдвое больший шум, чем модуляция PSK. Следовательно, при использовании DPSK следует ожидать вдвое (на 3 дБ) большей вероятности ошибки, чем в случае PSK; ухудшение качества передачи происходит довольно быстро с уменьшением отношения сигнал/шум (вопрос достоверности передачи при использовании модуляции DPSK рассмотрен в разделе 4.7.5). Преимуществом схемы DPSK можно назвать меньшую сложность системы.

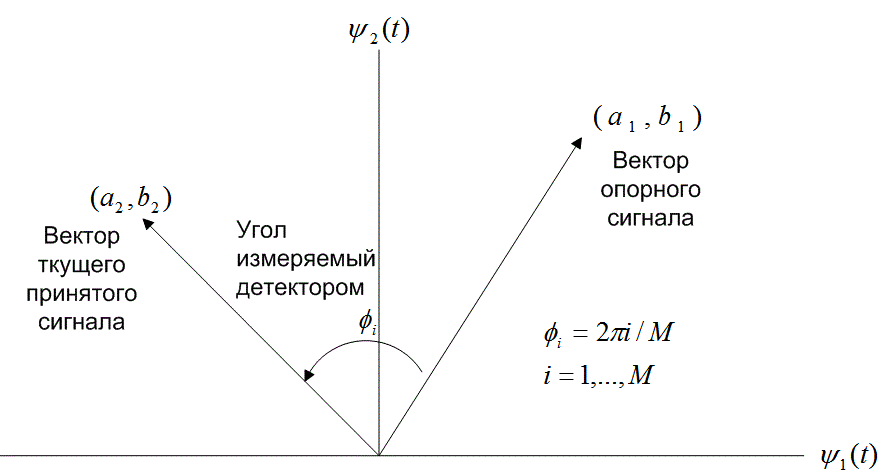
Рис. 4.16. Сигнальное пространство для схемы DPSK

4.5.2. Пример бинарной модуляции DPSK

Суть дифференциального когерентного обнаружения в схеме DPSK состоит в том, что информация из сигнала извлекается путем изменения фазы от символа к символу. Следовательно, переданный сигнал требуется вначале закодировать. На рис. 4.17, а представлено дифференциальное кодирование двоичного потока сообщений , где k — индекс дискретизации. Дифференциальное кодирование начинается (третья стро­ка на рисунке) с произвольного выбора первого бита кодовой последовательности c(k = 0) (в данном случае выбрана единица). Затем последовательность закодирован­ных битов c(k) может, в общем случае, кодироваться одним из двух способов.

(4.43)

или

(4.44)

Здесь символ "" представляет сложение по модулю 2 (определенное в разделе 2.9.3), а черта над выражением означает его дополнение. На рис. 4.17, а дифференциальное кодирование сообщения было выполнено с помощью уравнения (4.44). Другими сло­вами, текущий бит кода с(k) равен единице, если бит сообщения m(k) совпадает с пре­дыдущим закодированным битом c(k- 1), в противном случае — c(k)=0. В четвертой строке рисунка кодированная последовательность битов c(k) преобразовывается в по­следовательность сдвигов фаз , где единица представляется сдвигом фазы на 180°, а нуль — нулевым сдвигом фазы.

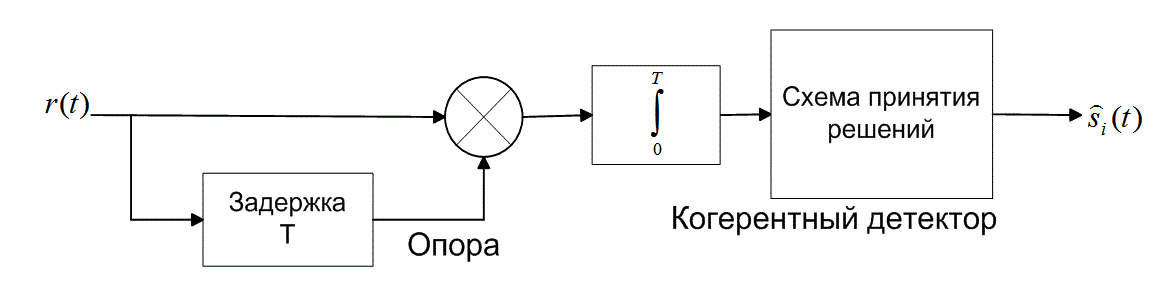
На рис. 4.17, б в виде блочной диаграммы представлена схема обнаружения бинарных сигналов в модуляции DPSK. Отметим, что основным элементом демодуля­тора на рис. 4.7 является интегратор произведений; как и при когерентном обнару­жении сигналов PSK, мы пытаемся определить корреляцию принятого сигнала с опорным. (Опорный сигнал — это просто запаздывающая версия принятого сигна­ла.) Другими словами, в течение каждого интервала передачи символа мы согласо­вываем принятый символ с предыдущим на предмет корреляции или антикорреля­ции (отличия в фазе на 180°).

а)

Обнаруженное сообщение, 1 1 0 1 0 1 1 0 0 1

б)

в)

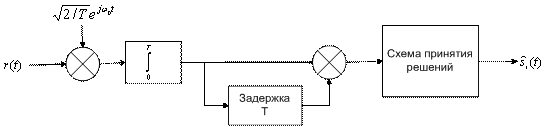
Рис. 4.17. Дифференциальная фазовая манипуляция (DPSK): а) дифференциальное кодирование; б) дифференциальное когерентное обнаружение; в) оптимальное дифференциальное когерентное обнаружение

Пусть при отсутствии шума принятый сигнал с последовательностью сдвигов фаз поступает в коррелятор, изображенный на рис. 4.17, б. Фаза совпадает с ; обе имеют одинаковое значение, π. Следовательно, первый бит обнаружен­ного выхода — . Далее совпадает с , и снова имеем то же значение . Затем отличается от , так что , и т.д.

Необходимо отметить, что детектор, изображенный на рис. 4.17, б, является близ­ким к оптимальному [3] в смысле вероятности ошибки. Оптимальный дифференци­альный детектор для схемы DPSK требует согласования опорной несущей с принятой несущей по частоте, но не обязательно по фазе. Отсюда — вид оптимального диффе­ренциального детектора, приведенного на рис. 4.17, в [4]. Достоверность передачи при использовании такого детектора рассмотрена в разделе 4.7.5. Обратите внимание на то, что опорный сигнал (рис. 4.17, в) приведен в комплексной форме записи ; это показывает необходимость квадратурной реализации, использующей квадратурный и синфазный компоненты (см. раздел 4.6.1).

4.5.3. Некогерентное обнаружение сигналов FSK

Детектор, выполняющий некогерентное обнаружение сигналов в модуляции FSK, описываемых уравнением (4.8), можно реализовать с помощью корреляторов, подобных показанным на рис. 4.7. При этом оборудование приема следует настроить как детектор энергии без измерения фазы. По этой причине некогерентный детектор обычно требует вдвое большего числа ветвей-каналов, чем когерентный. На рис. 4.18 показаны синфазный (I) и квадратурный (Q) каналы, используемые для некогерентного обнаружения набора сигналов в бинарной модуляции FSK (BFSK). Отметим, что две верхние ветви настроены на обнаружение сигнала с частотой для синфазной ветви опорный сигнал имеет вид , а для квадратурной — . Подобным образом две нижние ветви настроены на обнаружение сигнала с частотой ; для синфазной ветви опорный сигнал имеет вид , а для квадратурной — . Предположим, что принятый сигнал r(t) имеет вид точно , т.е. фаза точно равна нулю. Следовательно, сигнальный компонент принятого сигнала точно соответствует (по частоте и фазе) опорному сигналу верхней ветви. В такой ситуации максимальный выход должен дать интегратор произведений верхней ветви. Вторая ветвь должна дать нулевой выход (проинтегрированный шум с нулевым средним), поскольку ее опорный сигнал ортогонален сигнальному компоненту сигнала r(t). При ортогональной передаче сигналов (см. раздел 4.5.4) третья и четвертая ветви также должны дать выходы порядка нуля, поскольку их опорные сигналы также ортогональны сигнальному компоненту сигнала r(t).

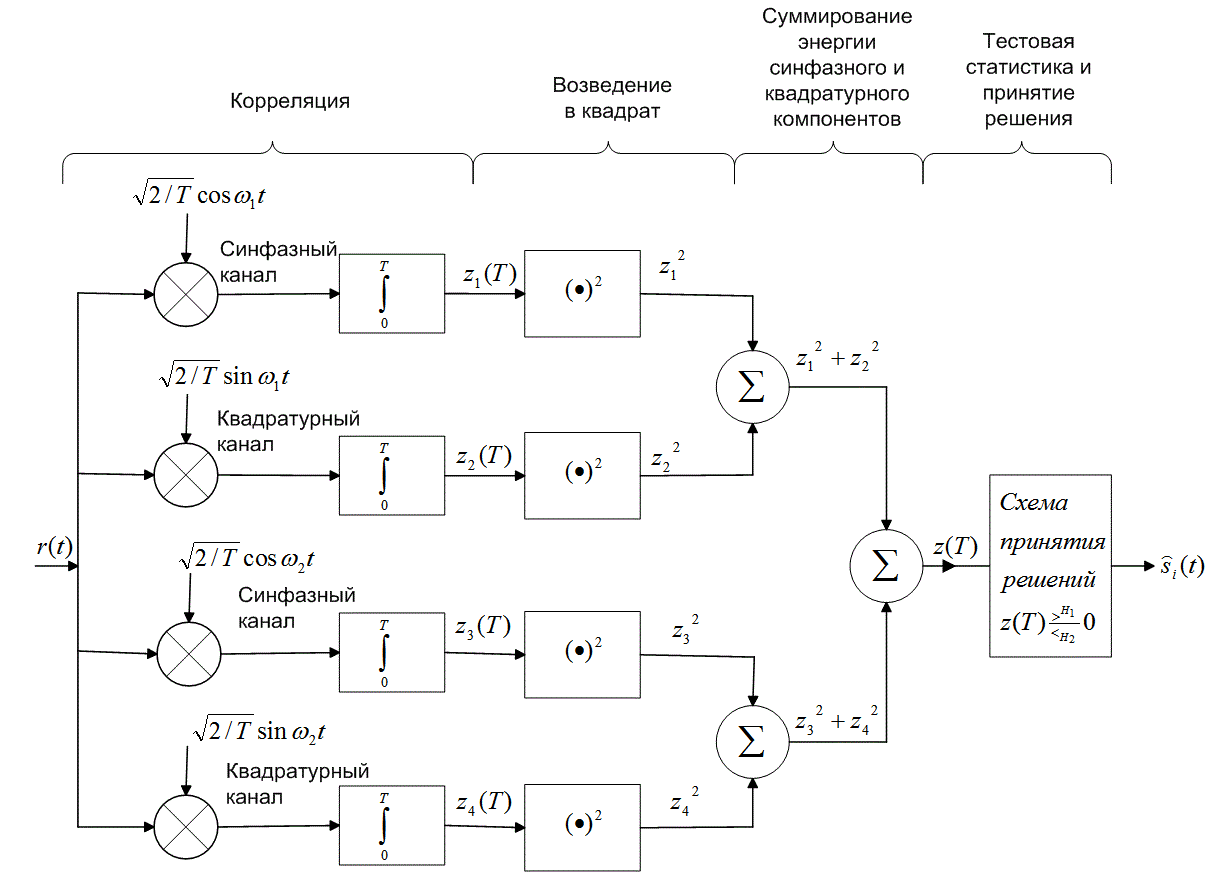
Рис. 4.18. Квадратурный приемник

Рассмотрим теперь другую возможность. Пусть принятый сигнал r(t) имеет вид . В этом случае максимальный выход должна дать вторая ветвь схемы (рис. 4.18), а выходы других ветвей должны быть порядка нуля. В реальной системе сигнал r(t) скорее всего описывается выражением , т.е. входящий сигнал будет частично коррелировать с опорным сигналом и частично — с сигналом . Поэтому некогерентный квадратурный приемник ортогональных сигналов и требует синфазной и квадратурной ветви для каждого возможного сигнала набора. Блоки, показанные на рис. 4.18 после интеграторов произведений, выполняют операцию возведения в квадрат, что предотвращает появление возможных отрицательных значений. Затем для каждого класса сигналов набора (в бинарном случае — для двух) складываются величины из синфазного канала и из квадратурного канала. На конечном этапе формируется тестовая статистика z(T) и выбирается сигнал с частотой , или , в зависимости от того, какая пара детекторов энергии дала максимальный выход.

Существует еще одна возможная реализация некогерентного обнаружения сигналов FSK. В этом случае используются полосовые фильтры, центрированные на частоте с полосой , за которыми, как показано на рис. 4.19, следуют детекторы огибающей (envelope detector). Детектор огибающей состоит из выпрямителя и фильтра нижних частот. Детекторы согласовываются с огибающими сигнала, а не с самими сигналами. При определении огибающей фаза несущей не имеет значения. При бинарной FSK решение относительно значения переданного символа принимается путем определения, какой из двух детекторов огибающей дает большую амплитуду на момент измерения. Подобным образом для системы, использующей многочастотную фазовую манипуляцию (multiple frequency shift-keying — MFSK), решение относительно принадлежности переданного символа к одному из М возможных принимается путем определения, какой из М детекторов огибающей дает максимальный выход.

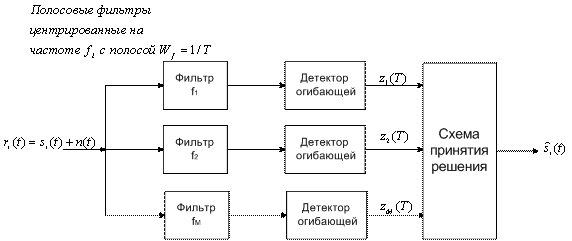
Рис. 4.19. Некогерентное обнаружение сигналов FSK с использованием детекторов огибающей

Детектор огибающей, изображенный на блочной диаграмме рис. 4.19, кажется проще квадратурного приемника, показанного на рис. 4.18, но не стоит забывать, что использование (аналоговых) фильтров обычно приводит к большей массе и стоимости детекторов огибающей по сравнению с квадратурным приемником. Поскольку квадратурные приемники могут реализовываться цифровым образом, с появлением больших интегральных схем их использование в качестве некогерентных детекторов стало предпочтительнее. Детектор, показанный на рис. 4.19, может реализовываться цифровым образом, использование аналоговых фильтров заменяется выполнением дискретного преобразования Фурье. Подобная структура обычно сложнее цифровой реализации квадратурного приемника.

4.5.4. Расстояние между тонами для некогерентной ортогональной передачи сигналов FSK

Частотная манипуляция (frequency shift keying — FSK) обычно реализуется как ортогональная передача сигналов, хотя ортогональными являются не все схемы FSK. Что мы подразумеваем под ортогональностью, когда речь идет о тонах сигнального множества? Предположим, что мы используем два тона f1= 10000 Гц и f2 = 11000 Гц. Ортогональны ли они между собой? Другими словами, удовлетворяют ли они критерию ортогональности (уравнение (3.39)) и не коррелируют ли в течение периода передачи символа T? Пока у нас недостаточно информации, чтобы ответить на этот вопрос. Вообще, тоны f1, и f2 являются ортогональными, если при переданном тоне f1 дискретная огибающая на выходе принимающего фильтра, согласованного с f2, дает нуль (т.е. отсутствуют перекрестные помехи). Подобная ортогональность между тонами сигнального множества FSK обеспечивается, если любая пара тонов множества разделена по частоте расстоянием, кратным 1/Г Гц. (Это доказывается ниже, в примере 4.3.) Тон с частотой f1, который включается на время передачи символа (Т с) и после этого выключается (такой, как тон FSK, приведенный в выражении (4.8)), аналитически можно описать следующим образом.

где

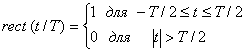
Из табл. А.1 находим Фурье-образ .

Здесь функция sinс определена выражением (1.39). Спектры подобных соседствующих тонов — тона 1 с частотой f1, и тона 2 с частотойf2 — показаны на рис. 4.20.

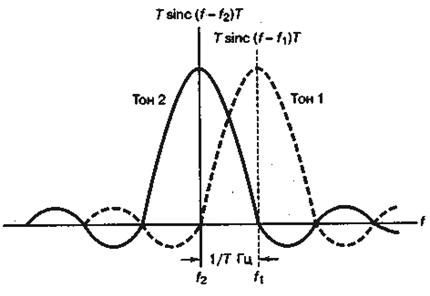
Рис. 4.20. Минимальное расстояние между тонами для ортогональной передачи сигналов FSK с некогерентным обнаружением

4.5.4.1. Минимальное расстояние между тонами и ширина полосы

Для того чтобы некогерентно обнаруживаемый тон давал максимальный сигнал на выходе "своего" фильтра и нулевой сигнал — на выходе любого соседнего фильтра (схема на рис. 4.19), максимум спектра тона 1 должен совпадать с одним из переходов через нуль спектра тона 2, а максимум спектра тона 2 должен приходиться на один из переходов через нуль спектра тона 1. Расстояние по частоте между центром спектрального главного лепестка и первым переходом через нуль является минимальным необходимым расстоянием между тонами. При некогерентном обнаружении это соответствует минимальному расстоянию между тонами, которое, как показано на рис. 4.20, равно 1/Т Гц. Несмотря на то что использование схемы FSK подразумевает передачу в течение каждого интервала передачи символа всего одного однополосного тона, когда мы говорим о ширине полосы сигнала, подразумеваем спектр, достаточный для всех тонов M-арного множества. Следовательно, для модуляции FSK требования к полосе связаны со спектральным расстоянием между тонами. Можно считать, что с каждым из группы соседствующих тонов связан спектр, простирающийся в обе стороны от максимального значения на величину, равную половине расстояния между тонами. Следовательно, для бинарной модуляции FSK, изображенной на рис. 4.20, ширина полосы передачи равна спектру, находящемуся между тонами, плюс области слева и справа, ширина которых равна половине расстояния между тонами. Общий спектр, таким образом, равен удвоенному расстоянию между тонами. Экстраполируя этот результат на M-арный случай, получаем, что ширина полосы сигнала в ортогональной модуляции MFSK с некогерентным обнаружением равна M/T.

До сих пор мы рассматривали только некогерентное обнаружение сигналов в ортогональной модуляции FSK. Будет ли отличаться критерий минимального расстояния между тонами (и, как следствие, ширина полосы) при когерентном обнаружении? Разумеется, да. Как будет показано ниже, в примере 4.3, при использовании когерентного обнаружения минимальное расстояние между тонами снижается до 1/2T.

4.5.4.2. Дуальные соотношения

Инженерную концепцию дуальности можно определить следующим образом. Два процесса (функции, элемента или системы) дуальны друг другу, если описывающие их математические соотношения идентичны, с точностью до фигурирующих в них переменных (например, время и частота). Рассмотрим передачу сигналов FSK, где, как показано на рис. 4.20, модулированные сигналы имеют вид функций sinc (fT). Данная длительность тона определяет минимальное расстояние по частоте между тонами, необходимое для получения ортогональности. Это соотношение в частотной области имеет дуальное ему во временной области — передачу импульсов (рис. 3.16, б), где прямоугольным участкам полосы соответствуют импульсы вида sine (tIT). Данная ширина полосы определяет минимальное расстояние (на временной оси) между импульсами, необходимое для получения нулевой межсимвольной интерференции.

Пример 4.3. Минимальное расстояние между тонами для ортогональной FSK

Рассмотрим два сигнала и , используемые для некогерентной передачи сигналов FSK, где . Скорость передачи символов равна 1/Т символов/с, где Т — длительность символа, а φ — произвольный постоянный угол между 0 и 2π.

а) Докажите, что минимальное расстояние между тонами для ортогональной передачи сигналов FSK с некогерентным обнаружением равно 1/Т.

б) Чему равно минимальное расстояние между тонами для ортогональной передачи сигналов FSK с когерентным обнаружением?

Решение

а) Чтобы два сигнала были ортогональными, они должны удовлетворять условию ортогональности, которое дается выражением (3.69).

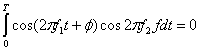(4.45)

Используя основные тригонометрические соотношения, приведенные в формулах (Г.6)и(ГЛ)-(Г.З), можно переписать выражение (4.4S) в виде

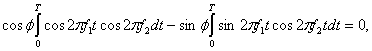(4.46)

так что

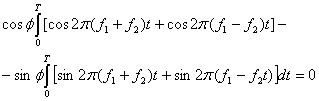(4.47)

что дает

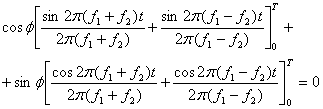(4.48)

или

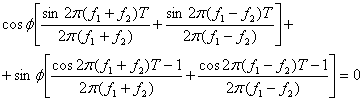(4.49)

Далее можно предположить, что ; это позволяет записать следующее.

(4.50)

Затем, объединяя выражения (4.49) и (4.50), можем записать следующее.

(4.51)

Отметим, что при произвольной фазе φ выражение (4.51) всегда справедливо, только если и при этом .

Поскольку

и

,

где п и k — целые, условия sin х = 0 и cos x = 1 удовлетворяются одновременно при п = 2k, Следовательно, из формулы (4.51) для произвольного φ можем записать следующее.

 

или (4.52)

Минимальное расстояние между тонами для ортогональной передачи сигналов FSK с некогерентным обнаружением получаем при к = 1, при этом

(4.53)

Напомним вопрос, сформулированный выше. Имея два тона f1 = 10 000 Гц и f2 = 11 000 Гц, мы спрашивали, являются ли они ортогональными? Теперь у нас достаточно информации для ответа на поставленный вопрос. Ответ связан со скоростью передачи сигналов FSK. Если манипуляция сигналами (переключение сигналов) происходит со скоростью 1 000 символов/с и используется некогерентное обнаружение, то сигналы ортогональны. Если манипуляция происходит быстрее, скажем со скоростью 10 000 символов/с, сигналы не ортогональны.

б) При некогерентном обнаружении, рассмотренном в п. а, расстояние между тонами, превращающее сигналы в ортогональные, было найдено посредством выполнения уравнения (4.45) для любой произвольной фазы. В случае когерентного обнаружения расстояние между тонами находится, если положить φ = 0. Причина в том, что мы знаем фазу принятого сигнала (ее дает контур ФАПЧ). Этот принятый сигнал будет коррелировать с каждым опорным сигналом, причем в качестве фазы опорного сигнала используется фаза принятого сигнала. Уравнение (4.51) можно теперь переписать с учетом φ = 0.

(4.54)

или

(4.55)

Минимальное расстояние между тонами для ортогональной передачи сигналов FSK с когерентным обнаружением получаем при k=l, при этом

(4.56)

Следовательно, при одинаковых скоростях передачи символов когерентное обнаружение требует меньшей ширины полосы, чем некогерентное, обеспечивая при этом ортогональную передачу сигналов. Можно сказать, что передача сигналов FSK с когерентным обнаружением более эффективно использует полосу. (Вопрос эффективности использования полосы подробно рассмотрен в главе 9.)

При когерентном обнаружении тоны расположены более плотно, чем при некогерентном, поскольку, если расположить два периодических сигнала так, чтобы их начальные фазы совпадали, ортогональность будет получена автоматически в силу симметрии (четности и нечетности) соответствующих сигналов в течение одного периода передачи символа. Это является отличием от способа получения ортогональности в п. а, где мы не уделяли внимания фазе. В случае когерентного обнаружения регулировка фазы в разрядах коррелятора означает, что мы можем расположить тоны ближе (по частоте) друг к другу, при этом по-прежнему поддерживая ортогональность в наборе тонов FSK. Вы можете доказать это самостоятельно, изобразив две синусоиды (или косинусоиды, или последовательности прямоугольных импульсов). Начальная фаза всех сигналов должна быть одинаковой (удобнее всего взять ее равной 0 радиан). Используя миллиметровку, выберите удобную временную шкалу для представления одного периода передачи символа Т. Изобразите тон с периодом Т, а затем изобразите другой тон, имеющий такую же начальную фазу, как и предыдущий, и период 2/3T. Выполните численное суммирование произведений тонов (смещенных относительно друг друга на 1/2T) и докажите, что они действительно являются ортогональными.

4.6. Комплексная огибающая

Описание реальных модуляторов и демодуляторов облегчается при использовании комплексной формы записи, введенной в разделе 4.2.1. Любой реальный полосовой сигнал s(t) можно представить в комплексной форме как

(4.57)

где g(t) — комплексная огибающая (complex envelop), которую можно записать следующим образом.

(4.58)

Амплитуда комплексной огибающей выражается как

, (4.59)

а фаза определяется следующим образом.

(4.60)

В формуле (4.57) g(t) можно называть полосовым сообщением или данными в комплексной форме, а — несущей в комплексной форме. Произведение этих двух величин представляет операцию модулирования, a s(t), действительная часть произведения, — это переданный сигнал. Следовательно, используя формулы (4.4), (4.57) и (4.58), s(t) можно выразить следующим образом.

(4.61)

Отметим, что модулирование сигналов, выраженное в общей форме (а + ib), умноженное на (с + id), дает сигнал с переменой знака (в квадратурном члене несущей волны) вида ас - bd.

4.6.1. Квадратурная реализация модулятора

Рассмотрим узкополосный сигнал g(t), который представлен последовательностью идеальных импульсов x(t) и y(t), передаваемых в дискретные моменты времени k = 1,2,.... Таким образом, g(t), x(t) и y(t) в уравнении (4.58) можно записывать как gk, xk и yt. Пусть значения амплитуд импульсов равны xk=yk=0,101A. При этом комплексную огибающую можно выразить в дискретной форме следующим образом.

(4.62)

Из комплексной алгебры знаем, что , но с практической точки зрения i можно рассматривать как "метку", напоминающую, что мы не можем использовать обычное сложение при группировке членов в формуле (4.62). Далее мы будем рассматривать синфазную и квадратурную модуляции, xk и yt, как упорядоченную пару. Модулятор, реализованный по квадратурному принципу, показан на рис. 4.21, где можно видеть, что импульс xk умножается на (синфазный компонент несущей), а импульс yt — на (квадратурный компонент несущей). Процесс модулирования можно кратко описать как умножение комплексной огибающей на с последующей передачей действительной части произведения. Итак, записываем следующее.

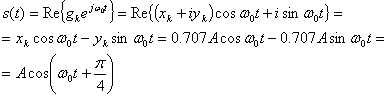(4.63)

Снова напомним, что квадратурный член несущей включает перемену знака в процессе модуляции. Если в качестве опорного сигнала использовать , то при передаче сигнала s(t) (уравнение (4.63)) происходит сдвиг опоры на π/4. Если же в качестве опорного сигнала применить , то переданный сигнал s(t) в уравнении (4.63) приводит к запаздыванию опоры на π/4. Графическая иллюстрация сказанного приведена на рис. 4.22

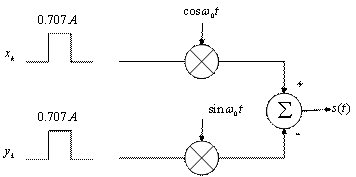
Рис. 4.21. Модулятор работающий по квадратурному принципу

4.6.2. Пример модулятора D8PSK

На рис. 4.23 изображена квадратурная реализация модулятора дифференциальной восьмифазной манипуляции (differential 8-PSK — D8PSK). Поскольку модуляция является 8-ричной, каждому информационному вектору , который можно записать как

(4.64)

присваивается 3-битовое сообщение (xk, yk, zk).

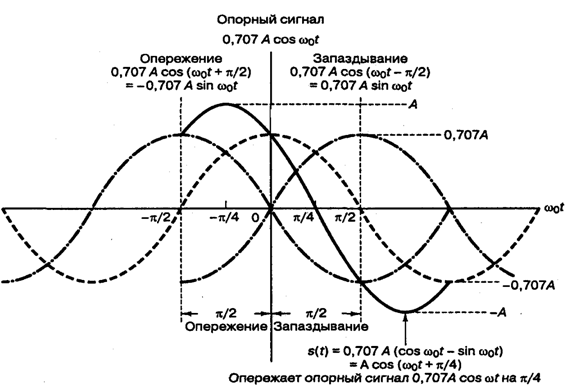
Рис. 4.22. Опережение/запаздывание синусоид

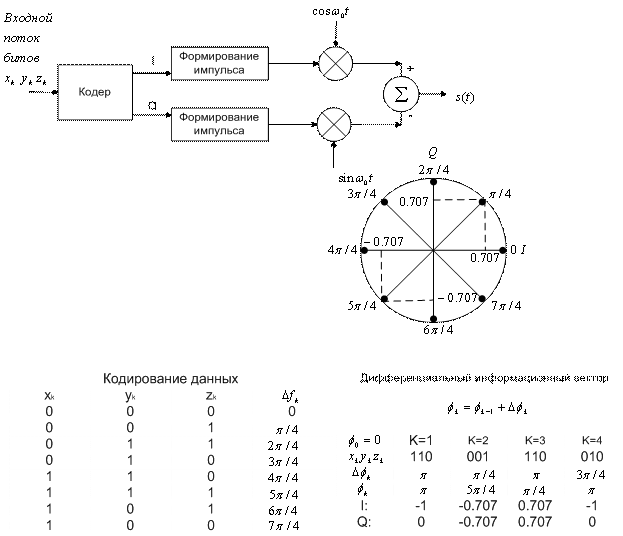
Рис. 4.23. Квадратурная реализация модулятора D8PSK

Сложение текущего кодируемого сообщения, выраженного разностью фаз с предыдущей фазой обеспечивает дифференциальное кодирование сообщений. Последовательность векторов, созданная с использованием уравнения (4.64), подобна результатам дифференциального кодирования, полученного с помощью процедуры, описанной в разделе 4.5.2. Можно заметить (рис. 4.23), что в результате кодирования 3-битовых последовательностей сообщений разностями фаз получаем не двоичную последовательность от 000 до 111, а специальный код, называемый кодом Грея (Gray code). (Преимущества использования подобного кода приведены в разделе 4.9.4.)

Пусть на вход модулятора, изображенного на рис. 4.23, в моменты времени k= 1, 2, 3, 4 поступают информационные последовательности 110, 001, 110, 010. Далее используем таблицу кодирования данных, приведенную на рис. 4.23, формулу (4.64) и, кроме того, положим начальную фазу (момент времени k = 0) равной нулю: = 0. В момент времени k = 1 дифференциальная информационная фаза, соответствующая набору = 110, равна = 4π/4 = π. Считая амплитуду вращающегося вектора единичной, синфазный (I) и квадратурный (Q) узкополосные импульсы равны -1 и 0. Как показано на рис. 4.23, форму этих импульсов обычно задает фильтр (такой, как фильтр с характеристикой типа приподнятого косинуса).

Для момента k = 2 таблица на рис. 4.23 показывает, что сообщение 001 кодируется сдвигом фаз = π/4. Следовательно, согласно формуле (4.64), вторая дифференциальная информационная фаза равна , и в момент k=2 синфазный и квадратурный узкополосные импульсы равны, соответственно, xk = -0,707 и yk = -0,707. Переданный сигнал имеет вид, приведенный в формуле (4.61).

(4.65)

Для сигнального множества, которое может представляться в координатах "фаза-амплитуда", такого как MPSK или MQAM, уравнение (4.65) позволяет сделать интересное наблюдение. Из него видно, что квадратурная реализация передатчика сводит все типы передачи сигналов к единственной амплитудной модуляции. Каждый вектор на плоскости передается посредством амплитудной модуляции его синфазной и квадратурной проекций на синусоидный и косинусоидный компоненты его несущей. В каждом случае процесс формирования импульса считается идеальным, т.е. предполагается, что информационные импульсы имеют идеальные прямоугольные формы. Таким образом, используя уравнение (4.65) для момента k = 2, при xk = -0,707 и yk = -0,707, можно записать переданный сигнал s(t) следующим образом.

(4.66)

4.6.3. Пример демодулятора D8PSK

В предыдущем разделе описание квадратурной реализации модулятора начиналось с умножения комплексной огибающей (узкополосного сообщения) на с последующей передачей действительной части произведения s(t), описанного в формуле (4.63). Демодулятор подобной схемы включает обратный процесс, т.е. умножение принятого полосового сигнала на с целью восстановления узкополосного сигнала. В левой части рис. 4.24 в упрощенном виде показан модулятор, изображенный на рис. 4.23, и сигнал , переданный в момент времени k = 2 (продолжаем использовать пример, описанный в предыдущем разделе). В правой части рис. 4.24 показана квадратурная реализация демодулятора.

Рис. 4.24. Пример модулятора/демодулятора

Отметим тонкое отличие между членом в модуляторе и демодуляторе. В модуляторе знак "минус" появляется при определении действительной части комплексного сигнала (произведения комплексной огибающей и комплексной несущей). В демодуляторе член появляется при умножении полосового сигнала на сопряженное несущей модулятора. Демодуляция является когерентной, если фаза восстанавливается. Для упрощения записи основных соотношений процесса мы пренебрегаем шумом. Итак, после синфазного умножения в демодуляторе на в точке А получаем следующий сигнал.

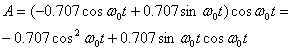(4.67)

Используя тригонометрические соотношения, приведенные в формулах (Г.7) и (Г.9), получаем следующее.

(4.68)

После фильтрации с использованием фильтра нижних частот (low-pass filter — LPF) в точке А' восстанавливается идеальный отрицательный импульс.

(с точностью до масштабного коэффициента) (4.69)

Подобным образом после квадратурного умножения в демодуляторе на в точке В получаем сигнал.

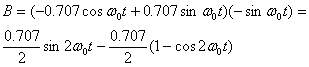(4.70)

После прохождения сигналом фильтра нижних частот в точке В' восстанавливается идеальный отрицательный импульс.

(с точностью до масштабного коэффициента) (4.71)

Таким образом, видим, что в точках A' и В' (идеальные) дифференциальные информационные импульсы для синфазного и квадратурного каналов равны -0,707. Поскольку модулятор/демодулятор является дифференциальным, для нашего примера k=2 получаем следующее.

(4.72)

Будем считать, что в предыдущий момент времени k = 1 демодулятор правильно определил, что фаза сигнала равна π. Тогда из формулы (4.72) можем получить следующее.

(4.73)

Вернувшись к таблице модуляции на рис. 4.23, видим, что данной фазе соответствует информационная последовательность = 001, что совпадает с данными, посланными в момент времени k = 2.

4.7. Вероятность ошибки в бинарных системах

4.7.1. Вероятность появления ошибочного бита при когерентном обнаружении сигнала BPSK

Важной мерой производительности, используемой для сравнения цифровых схем модуляции, является вероятность ошибки, РЕ Для коррелятора или согласованного фильтра вычисление РЕ можно представить геометрически (см. рис. 4.6). Расчет РЕ включает нахождение вероятности того, что при данном векторе переданного сигнала, скажем si вектор шума n выведет сигнал из области 1. Вероятность принятия детектором неверного решения называется вероятностью символьной ошибки, рE. Несмотря на то что решения принимаются на символьном уровне, производительность системы часто удобнее задавать через вероятность битовой ошибки (Ps). Связь РВ и РЕ рассмотрена в разделе 4.9.3 для ортогональной передачи сигналов и в разделе 4.9.4 для многофазной передачи сигналов.

Для удобства изложения в данном разделе мы ограничимся когерентным обнаружением сигналов BPSK. В этом случае вероятность символьной ошибки — это то же самое, что и вероятность битовой ошибки. Предположим, что сигналы равновероятны. Допустим также, что при передаче сигнала принятый сигнал r(t) равен , где n(t) — процесс AWGN; кроме того, мы пренебрегаем ухудшением качества вследствие введенной каналом или схемой межсимвольной интерференции. Как показывалось в разделе 4.4.1, антиподные сигналы и можно описать в одномерном сигнальном пространстве, где

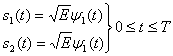(4.74)

Детектор выбирает с наибольшим выходом коррелятора ; или, в нашем случае антиподных сигналов с равными энергиями, детектор, используя формулу (4.20), принимает решение следующего вида.

(4.74)

Как видно из рис. 4.9, возможны ошибки двух типов: шум так искажает переданный сигнал , что измерения в детекторе дают отрицательную величину z(T), и детектор выбирает гипотезу H2, что был послан сигнал s2(t). Возможна также обратная ситуация: шум искажает переданный сигнал , измерения в детекторе дают положительную величину z(T), и детектор выбирает гипотезу Н1, соответствующую предположению о передаче сигнала .

В разделе 3.2.1.1 была выведена формула (3.42), описывающая вероятность битовой ошибки РB для детектора, работающего по принципу минимальной вероятности ошибки.

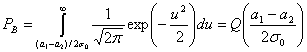(4.76)

Здесь σ0 — среднеквадратическое отклонение шума вне коррелятора. Функция Q(x), называемая гауссовым интегралом ошибок, определяется следующим образом.

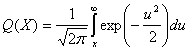(4.77)

Эта функция подробно описывается в разделах 3.2 и Б.3.2.

Для передачи антиподных сигналов с равными энергиями, таких как сигналы в формате BPSK, приведенные в выражении (4.74), на выход приемника поступают следующие компоненты: , при переданном сигнале , и , при переданном сигнале s2(t), где Еь — энергия сигнала, приходящаяся на двоичный символ. Для процесса AWGN дисперсию шума вне коррелятора можно заменить N0/2 (см. приложение В), так что формулу (4.76) можно переписать следующим образом.

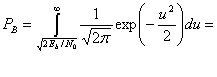(4.78)

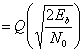(4.79)

Данный результат для полосовой передачи антиподных сигналов BPSK совпадает с полученными ранее формулами для обнаружения антиподных сигналов с использованием согласованного фильтра (формула (3.70)) и обнаружения узкополосных антиподных сигналов с применением согласованного фильтра (формула (3.76)). Это является примером описанной ранее теоремы эквивалентности. Для линейных систем теорема эквивалентности утверждает, что на математическое описание процесса обнаружения не влияет сдвиг частоты. Как следствие, использование согласованных фильтров или корреляторов для обнаружения полосовых сигналов (рассмотренное в данной главе) дает те же соотношения, что были выведены ранее для сопоставимых узкополосных сигналов.

4.7.2. Вероятность появления ошибочного бита при когерентном обнаружении сигнала в дифференциальной модуляции BPSK

          Сигналы в канале иногда инвертируются; например, при использовании когерентного опорного сигнала, генерируемого контуром ФАПЧ, фаза может быть неоднозначной. Если фаза несущей была инвертирована при использовании схемы DPSK, как это скажется на сообщении? Поскольку информация сообщения кодируется подобием или отличием соседних символов, единственным следствием может быть ошибка в бите, который инвертируется, или в бите, непосредственно следующим за инвертированным. Точность определения подобия или отличия символов не меняется при инвертировании несущей. Иногда сообщения (и кодирующие их сигналы) дифференциально кодируются и когерентно обнаруживаются, чтобы просто избежать неопределенности в определении фазы.

          Вероятность появления ошибочного бита при когерентном обнаружении сигналов в дифференциальной модуляции PSK (DPSK) дается выражением [5].

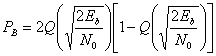                                          (4.80)

         Это соотношение изображено на рис. 4.25. Отметим, что существует незначительное ухудшение достоверности обнаружения по сравнению с когерентным обнаружением сигналов в модуляции PSK. Это вызвано дифференциальным кодированием, поскольку любая отдельная ошибка обнаружения обычно приводит к принятию двух ошибочных решений. Подробно вероятность ошибки при использовании наиболее популярной схемы — когерентного обнаружения сигналов в модуляции DPSK — рассмотрена в разделе 4.7.5.

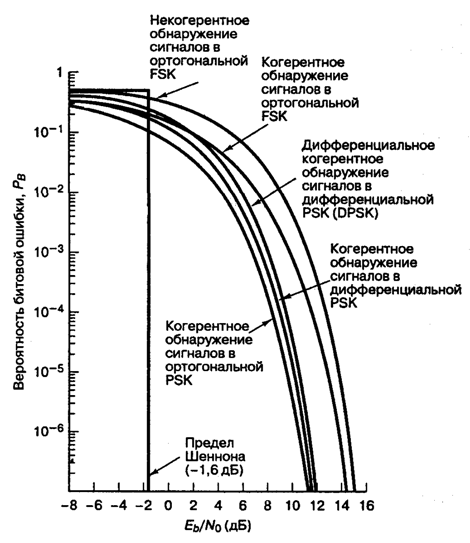
Рис. 4.25. Вероятность появления ошибочного бита для бинарных систем нескольких типов

4.7.3. Вероятность появления ошибочного бита при когерентном обнаружении сигнала в бинарной ортогональной модуляции FSK

Формулы (4.78) и (4.79) описывают вероятность появления ошибочного бита для когерентного обнаружения антиподных сигналов. Более общую трактовку для когерентного обнаружения бинарных сигналов (не ограничивающихся антиподными сигналами) дает следующее выражение для РВ [6].

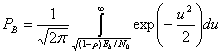(4.81)

Из формулы (3.64,б) — временной коэффициент взаимной корреляций между и , где θ — угол между векторами сигналов и s2 (см. рис. 4.6). Для антиподных сигналов, таких как сигналы BPSK, θ = π, поэтому ρ = -1.

Для ортогональных сигналов, таких как сигналы бинарной FSK (BFSK), θ = π/2, поскольку векторы и s2 перпендикулярны; следовательно, ρ = 0, что можно доказать с помощью формулы (3.64,а), поэтому выражение (4.81) можно переписать следующим образом.

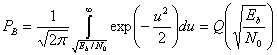(4.82)

Здесь Q(x) — дополнительная функция ошибок, подробно описанная в разделах 3.2 и Б.3.2. Зависимость (4.82) для когерентного обнаружения ортогональных сигналов BFSK, показанная на рис. 4.25, аналогична зависимости, полученной для обнаружения ортогональных сигналов с помощью согласованного фильтра (формула (3.71)) и узкополосных ортогональных сигналов (униполярных импульсов) с использованием согласованного фильтра (формула (3.73)). В данной книге мы не рассматриваем амплитудную манипуляцию ООК (on-off keying), но соотношение (4.82 применимо к обнаружению с помощью согласованного фильтра сигналов ООК, так же как и к когерентному обнаружению любых ортогональных сигналов.

Справедливость соотношения (4.82) подтверждает и то, что разность энергий между ортогональными векторами сигналов и s2 с амплитудой , как показано на рис. 3.10, б, равна квадрату расстояния между концами ортогональных векторов Ed = 2Eb. Подстановка этого результата в формулу (3.63) также дает формулу (4.82). Сравнивая формулы (4.82) и (4.79), видим, что, по сравнению со схемой BPSK, схема BFSK требует на 3 дБ большего отношения E/N0 для обеспечения аналогичной достоверности передачи. Этот результат не должен быть неожиданным, поскольку при данной мощности сигнала квадрат расстояния между ортогональными векторами вдвое (на 3 дБ) больше квадрата расстояния между антиподными векторами.

4.7.4. Вероятность появления ошибочного бита при некогерентном обнаружении сигнала в бинарной ортогональной модуляции FSK

Рассмотрим бинарное ортогональное множество равновероятных сигналов FSK , определенное формулой (4.8).

Фаза φ неизвестна и предполагается постоянной. Детектор описывается М = 2 каналами, состоящими, как показано на рис. 4.19, из полосовых фильтров и детекторов огибающей. На вход детектора поступает принятый сигнал r(t) = si(t) + n(t), где n(i) — гауссов шум с двусторонней спектральной плотностью мощности No/2. Предположим, что и достаточно разнесены по частоте, чтобы их перекрытием можно было пренебречь. Вычисление вероятности появления ошибочного бита для равновероятных сигналов и начнем, как и в случае узкополосной передачи, с уравнения (3.38).

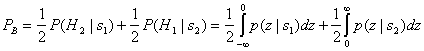(4.83)

Для бинарного случая тестовая статистика z(T) определена как . Предположим, что полоса фильтра Wf равна 1/T, так что огибающая сигнала FSK (приблизительно) сохраняется на выходе фильтра. При отсутствии шума в приемнике значение z(T) равно при передаче s1(t) и - — при передаче s2(t). Вследствие такой симметрии оптимальный порог γ0=0. Плотность вероятности подобна плотности вероятности .

(4.84)

Таким образом, можем записать

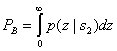(4.85)

или

(4.86)

где z1 и z2 обозначают выходы z1(T) и z2(T) детекторов огибающей, показанных на рис.4.19. При передаче тона , т.е. когда r(t) = s2(t) + n(t), выход z1(T) состоит исключительно из случайной переменной гауссового шума; он не содержит сигнального компонента. Распределение Гаусса в нелинейном детекторе огибающей дает распределение Релея на выходе [6], так что

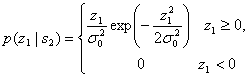(4.87)

где — шум на выходе фильтра. С другой стороны, z2(T) имеет распределение Раиса, поскольку на вход нижнего детектора огибающей подается синусоида плюс шум [6]. Плотность вероятности p(z2\s2) записывается как

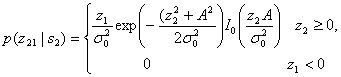(4.88)

где и, как и ранее, — шум на выходе фильтра. Функция 10(х), известная как модифицированная функция Бесселя первого рода нулевого порядка [7], определяется следующим образом.

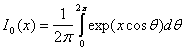(4.89)

Ошибка при передаче s2(t) происходит, если выборка огибающей z1(T), полученная из верхнего канала (по которому проходит шум), больше выборки огибающей z2(T), полученной из нижнего канала (по которому проходит сигнал и шум). Таким образом, вероятность этой ошибки можно получить, проинтегрировав до бесконечности с последующим усреднением результата по всем возможным z2.

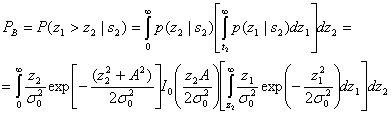(4.91)

Здесь , внутренний интеграл — условная вероятность ошибки, при фиксированном значении z2, если был передан сигнал s2(1), а внешний интеграл усредняет условную вероятность по всем возможным значениям z2. Данный интеграл можно вычислить аналитически [8], и его значение равно следующему.

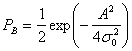(4.92)

С помощью формулы (1.19) шум на выходе фильтра можно выразить как

 

(4.93)

где a Wf — ширина полосы фильтра. Таким образом, формула (4.92) приобретает следующий вид.

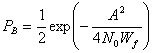(4.94)

 

Выражение (4.94) показывает, что вероятность ошибки зависит от ширины полосы полосового фильтра и РB уменьшается при снижении Wf. Результат справедлив только при пренебрежении межсимвольной интерференцией (intersymbol interference — ISI). Минимальная разрешенная Wf (т.е. не дающая межсимвольной интерференции) получается из уравнения (3.81) при коэффициенте сглаживания г = 0. Следовательно, Wf= R бит/с =1/T, и выражение (4.94) можно переписать следующим образом.

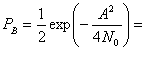(4.95)

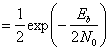(4.96)

Здесь Еь= (1/2)А²Т — энергия одного бита. Если сравнить вероятность ошибки схем некогерентной и когерентной FSK (см. рис. 4.25), можно заметить, что при равных РB некогерентная FSK требует приблизительно на 1 дБ большего отношения Eb/N0, чем когерентная FSK (для РB < 10^-4). При этом некогерентный приемник легче реализуется, поскольку не требуется генерировать когерентные опорные сигналы. По этой причине практически все приемники FSK используют некогерентное обнаружение. В следующем разделе будет показано, что при сравнении когерентной ортогональной схемы FSK с нёкогерентной схемой DPSK имеет место та же разница в 3 дБ, что и при сравнении когерентной ортогональной FSK и когерентной PSK. Как указывалось ранее, в данной книге не рассматривается амплитудная манипуляция ООК (on-off keying). Все же отметим, что вероятность появления ошибочного бита РB, выраженная в формуле (4.96), идентична РB для некогерентного обнаружения сигналов ООК.

4.7.5. Вероятность появления ошибочного бита для бинарной модуляции DPSK

Определим набор сигналов BPSK следующим образом.

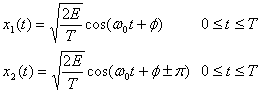(4.97)

Особенностью схемы DPSK является отсутствие в сигнальном пространстве четко определенных областей решений. В данном случае решение основывается на разности фаз между принятыми сигналами. Таким образом, при передаче сигналов DPSK каждый бит в действительности передается парой двоичных сигналов.

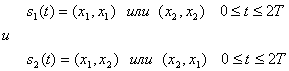(4.98)

Здесь обозначает сигнал , за которым следует сигнал . Первые Т секунд каждого сигнала — это в действительности последние Т секунд предыдущего. Отметим, что оба сигнала s1(t) и s2(t) могут принимать любую из возможных форм и что и — это антиподные сигналы. Таким образом, корреляцию между и s2(t) для любой комбинации сигналов можно записать следующим образом.

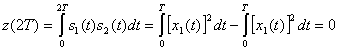(4.99)

Следовательно, каждую пару сигналов DPSK можно представить как ортогональный сигнал длительностью 2Т секунд. Обнаружение может соответствовать некогерентному обнаружению огибающей с помощью четырех каналов, согласованных с каждым возможным выходом огибающей, как показано на рис. 4.26. Поскольку два детектора огибающей, представляющих каждый символ, обратны друг другу, выборки их огибающих будут совпадать. Значит, мы можем реализовать детектор как один канал для , согласовывающегося с или , и один канал для , согласовывающегося с или , как показано на рис. 4.26. Следовательно, детектор DPSK сокращается до стандартного двухканального некогерентного детектора. В действительности фильтр может согласовываться с разностным сигналом; так что необходимым является всего один канал. На рис. 4.26 показаны фильтры, которые согласовываются с огибающими сигнала (в течение двух периодов передачи символа). Что это означает, если вспомнить, что DPSK — это схема передачи сигналов с постоянной огибающей? Это означает, что нам требуется реализовать детектор энергии, подобный квадратурному приемнику на рис. 4.18, где каждый сигнал в течение периода представляется синфазным и квадратурным опорными сигналами.

синфазный опорный сигнал квадратурный опорный сигнал синфазный опорный сигнал квадратурный опорный сигнал

Поскольку пары сигналов DPSK ортогональны, вероятность ошибки при подобном некогерентном обнаружении дается выражением (4.96). Впрочем, поскольку сигналы DPSK длятся 2Т секунд, энергия сигналов , определенных в формуле (4.98), равна удвоенной энергии сигнала, определенного в течение одного периода передачи символа.

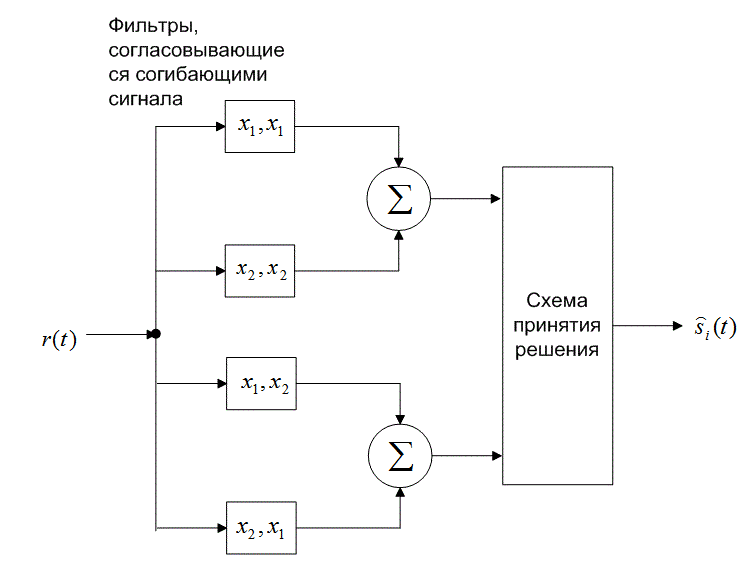
а)

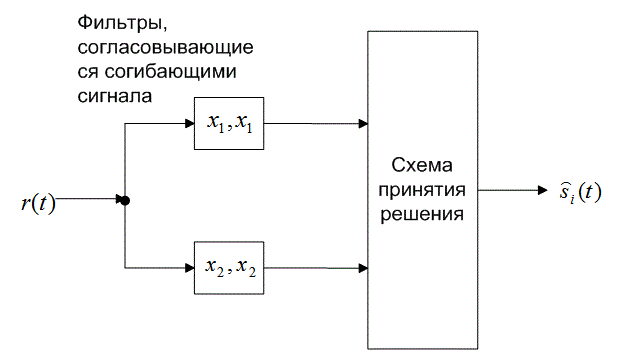
б)

Рис. 4.26. Обнаружение в схеме DPSK: а) четырехканальное дифференциально-когерентное обнаружение сигналов в бинарной модуляции DPSK; б) эквивалентный двухканальный детектор сигналов в бинарной модуляции DPSK

Таким образом, РВможно записать в следующем виде.

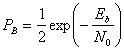(4.100)

Зависимость (4.100), изображенная на рис. 4.25, представляет собой дифференциальное когерентное обнаружение сигналов в дифференциальной модуляции PSK, или просто DPSK. Выражение справедливо для оптимального детектора DPSK (рис. 4.17, в). Для детектора, показанного на рис. 4.17, б, вероятность ошибки будет несколько выше приведенной в выражении (4.100) [3]. Если сравнить вероятность ошибки, приведенную в формуле (4.100), с вероятностью ошибки когерентной схемы PSK (см. рис. 4.25), видно, что при равных РB схема DPSK требует приблизительно на 1 дБ большего отношения E^N0, чем схема BPSK (для ). Систему DPSK реализовать легче, чем систему PSK, поскольку приемник DPSK не требует фазовой синхронизации. По этой причине иногда предпочтительнее использовать менее эффективную схему DPSK, чем более сложную схему PSK.

4.7.6. Вероятность ошибки для различных модуляций

          В табл. 4.1 и на рис. 4.25 приведены аналитические выражения и графики Р_B для наиболее распространенных схем модуляции, описанных выше. Для Р_B = 10^-4 можно видеть, что разница между лучшей (когерентной PSK) и худшей (некогерентной ортогональной FSK) из рассмотренных схем равна приблизительно 4 дБ. В некоторых случаях 4 дБ — это небольшая цена за простоту реализации, увеличивающуюся от когерентной схемы PSK до некогерентной FSK (рис. 4.25); впрочем, в других случаях ценным является даже выигрыш в 1 дБ. Помимо сложности реализации и вероятности Р_B существуют и другие факторы, влияющие на выбор модуляции; например, в некоторых случаях (в каналах со случайным затуханием) желательными являются некогерентные системы, поскольку иногда когерентные опорные сигналы затруднительно определять и использовать. В военных и космических приложениях весьма желательны сигналы, которые могут противостоять значительному ухудшению качества, сохраняя возможность обнаружения.

Таблица 4.1. Вероятность ошибки для различных бинарных модуляций

4.8. M-арная передача сигналов и производительность

4.8.1. Идеальная достоверность передачи

На рис. 3.6 приводился характерный, "водопадоподобный" график зависимости вероятности ошибки от отношения . Как видно из рис.4.25, вероятность появления ошибочного бита (РB) для различных бинарных схем модуляции при наличии AWGN также имеет подобную форму. А на что будет похож график зависимости идеальной РB от ? Ответ, в виде предела Шеннона, приведен на ри.с. 4.27. Этот предел представляет порог , ниже которого поддержание достоверной связи невозможно. Подробно работа Шеннона рассмотрена в главе 9.

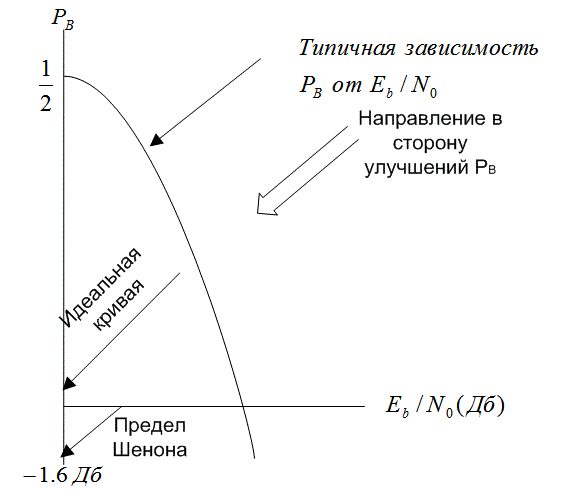
Рис. 4.27. Зависимость идеальной

Идеальную кривую на рис. 4.27 можно описать следующим образом. Для всех значений , находящихся выше предела Шеннона (-1,6 дБ), РB равно нулю. Как только падает ниже предела Шеннона, РB в худшем случае возрастает до 1/2. (Отметим, что РB = 1 — это не самый неблагоприятный вариант для бинарной передачи сигналов, поскольку это значение аналогично РB = 0; если вероятность появления ошибочного бита равна 100%, то для восстановления точной информации поток битов просто можно инвертировать.) На рис. 4.27 большой стрелкой показано направление повышения достоверности передачи от типичной к идеальной вероятности РB.

4.8.2. М-арная передача сигналов

Рассмотрим M-арную передачу сигналов. В каждый момент времени процессор рассматривает k бит. Он указывает модулятору произвести один из М=2^k сигналов; частным случаем k= 1 является бинарная передача сигналов. Как увеличение k влияет на достоверность передачи — снижает или повышает ее? (Не спешите отвечать — вопрос с подвохом.) На рис. 4.28 показана зависимость вероятности появления ошибочного бита для ортогональной M-уровневой передачи сигналов по каналу с гауссовым шумом при использовании когерентного обнаружения. На рис. 4.29 подобные графики приведены для многофазной передачи по каналу с гауссовым шумом при применении когерентного обнаружения. В каком направлении движется график при увеличении k (или М)? Из рис. 4.27 мы знаем, как изменяется кривая при увеличении и уменьшении вероятности ошибки. Поэтому можем сказать, что на рис. 4.28 по мере роста k график перемещается в направлении уменьшения вероятности ошибки. На рис. 4.29 рост k приводит к увеличению вероятности ошибки. Подобное передвижение свидетельствует, что М-арная передача сигналов уменьшает вероятность ошибки при ортогональной передаче сигналов и увеличивает — при многофазной передаче. Справедливо ли это? Почему вообще используют многофазную модуляцию PSK, если она приводит к высокой вероятности ошибки по сравнению с бинарной PSK? Сказанное действительно справедливо, и во многих системах действительно применяется многофазная передача сигналов. Подвох был в формулировке вопроса: там подразумевалось, что зависимость вероятности ошибки от Eb/N0 является единственным критерием качества. На самом деле существует множество других характеристик (например, ширина полосы, пропускная способность, сложность, стоимость), но на рис. 4.28 и 4.29 явно показана только вероятность ошибки.

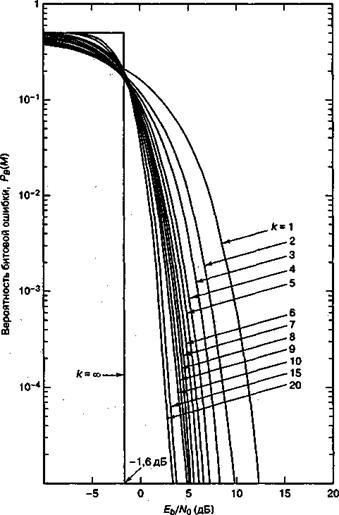
Рис. 4.28. Зависимость от для ортогональной М-арной передачи сигналов по каналу с гауссовым шумом при использовании когерентного обнаружения. (Перепечатано с разрешения авторов из работы W. C. Lindsey and M. K. Simon. Telecommunication System Engineering. Prentice Hall, Inc., Englewood Cliffs, N. J.)

 

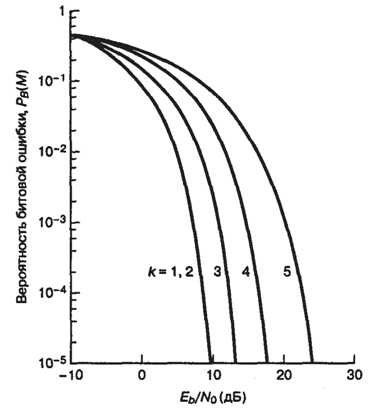
Рис. 4.29. Зависимость от для ортогональной многофазной передачи сигналов по каналу с гауссовым шумом при использовании когерентного обнаружения

Одной из рабочих характеристик, не представленных на рис. 4.28 и 4.29 явно, является необходимая ширина полосы. Для графиков на рис. 4.28 повышение значений k подразумевает увеличение требуемой ширины полосы. Для М-арных многофазных кривых, приведенных на рис. 4.29, рост величины k позволяет получать большую скорость передачи битов при той же ширине полосы. Другими словами, при фиксированной скорости передачи данных уменьшается необходимая полоса. Следовательно, графики вероятности ошибки и при ортогональной, и при многофазной передаче показывают, что М-арная передача сигналов представляет средство реализации компромиссов между параметрами системы. При ортогональной передаче сигналов повышение достоверности передачи может быть получено за счет расширения полосы. В случае многофазной передачи эффективность использования полосы может быть получена за счет вероятности ошибки.

4.8.3. Векторное представление сигналов MPSK

На рис. 4.30 показаны наборы сигналов MPSK для М - 2, 4, 8 и 16. На рис. 4.30, а видим бинарные (k=l, M = 2) антиподные векторы s, и s2, угол между которыми равен 180°. Граница областей решений разделяет сигнальное пространство на две области. На рисунке также показан вектор шума n, равный по амплитуде сигналу . При указанных направлении и амплитуде энергия вектора шума является минимальной, и детектор может допустить символьную ошибку.

На рис. 4.30, б видим 4-арные (k = 2, М = 4) векторы, расположенные друг к другу под углом 90°. Границы областей решений (на рисунке изображена только одна) делят сигнальное пространство на четыре области.

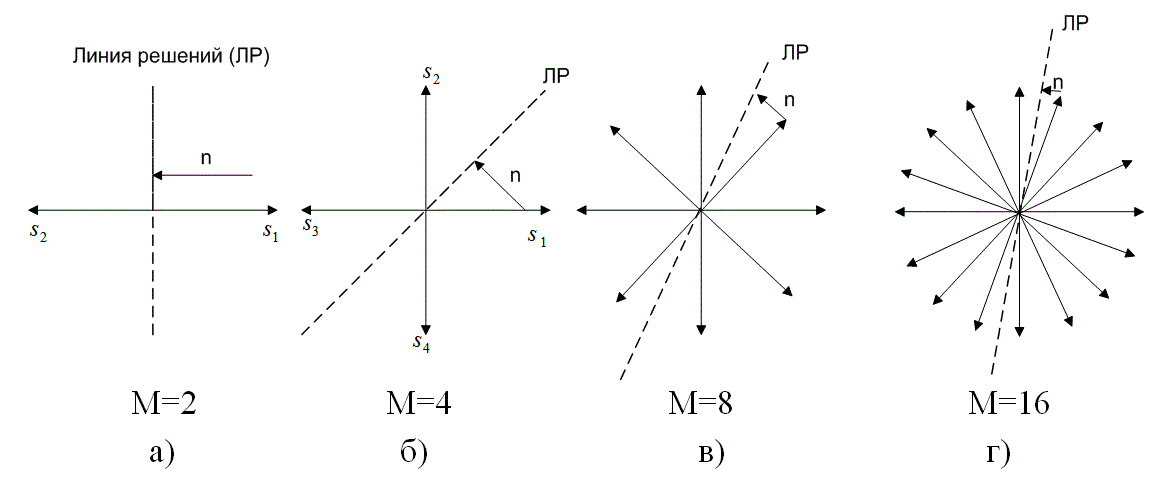
Рис. 4.30. Наборы сигналов MPSK для М = 2, 4, 8, 16

Здесь также изображен вектор шума n (начало — в вершине вектора сигнала, направление перпендикулярно ближайшей границе областей решений), являющийся вектором минимальной энергии, достаточной, чтобы детектор допустил символьную ошибку. Отметим, что вектор шума минимальной энергии на рис. 4.30, б меньше вектора шума на рис. 4.30, а, что свидетельствует о большей уязвимости 4-арной системы к шуму, по сравнению с бинарной (энергии сигналов в обоих случаях взяты равными). Изучая рис. 4.30, в, г, можно отметить следующую закономерность. При многофазной передаче сигналов по мере роста величины М на сигнальную плоскость помещается все больше сигнальных векторов. По мере того как векторы располагаются плотнее, для появления ошибки вследствие шума требуется все меньше энергии.

С помощью рис. 4.30 можно лучше понять поведение зависимости вероятности РВ от , изображенной на рис. 4.29, при росте k. Кроме того, рисунок позволяет взглянуть на природу компромиссов при многофазной передаче сигналов. Размещение большего числа векторов сигналов в сигнальном пространстве эквивалентно повышению скорости передачи данных без увеличения системной ширины полосы (все векторы ограничиваются одной и той же плоскостью). Другими словами, мы повысили использование полосы за счет вероятности ошибки. Рассмотрим рис. 4.30, г, где из приведенных вариантов вероятность ошибки является наивысшей. Чем мы может заплатить, чтобы "выкупить" возросшую вероятность ошибки? Иными словами, чем мы можем поступиться, чтобы расстояние между соседними векторами сигналов на рис. 4.30, д стало таким же, как на рис. 4.30, al Мы можем увеличивать интенсивность сигнала (сделать векторы сигналов длиннее), пока минимальное расстояние от вершины вектора сигнала до линии решений не станет равным размеру вектора шума на рис. 4.30, а. Таким образом, для многофазной системы по мере роста М мы можем увеличивать производительность полосы либо за счет повышения вероятности ошибки, либо за счет увеличения отношения .

Отметим, что на схемах, изображенных на рис. 4.30, а для различных значений М, все векторы имеют одинаковую амплитуду. Это равносильно утверждению, что сопоставление различных схем выполняется при фиксированном отношении , где — энергия символа. Сравнительные схемы можно сделать и при фиксированном отношении , в этом случае амплитуды векторов будут увеличиваться с ростом М. При М = 4, 8 и 16 амплитуды векторов будут, соответственно, в и 2 раза больше векторов для случая М = 2. Как и в предыдущем случае, с ростом М будет усиливаться восприимчивость к шуму, но она не будет такой явной, как на рис. 4.30.

4.8.4. Схемы BPSK и QPSK имеют одинаковые вероятности ошибки

В уравнении (3.30) было получено следующее соотношение между .

(4.101)

Здесь S — средняя мощность сигнала, a R — скорость передачи битов. Вероятность ошибки в сигнале BPSK с отношением , найденным из уравнения (4.101), определяется из кривой на рис. 4,29, соответствующей k = 1. Схему QPSK можно описать с помощью двух ортогональных каналов BPSK. Поток битов QPSK обычно разбивается на четный и нечетный (синфазный и квадратурный) потоки; каждый новый поток модулирует ортогональный компонент несущей со скоростью, вдвое меньшей скорости исходного потока. Синфазный поток модулирует член , а квадратурный — член . Если амплитуда исходного вектора QPSK была равна А, то амплитуды векторов синфазного и квадратурного компонентов равны, как показано на рис. 4.31, . Следовательно, на каждый квадратурный сигнал BPSK приходится половина средней мощности исходного сигнала QPSK. Значит, если исходный сигнал QPSK имел скорость R бит/с и среднюю мощность S Вт, квадратурное разбиение приводит к тому, что каждый сигнал BPSK имеет скорость передачи R/2 бит/с и среднюю мощность S/2 Вт.

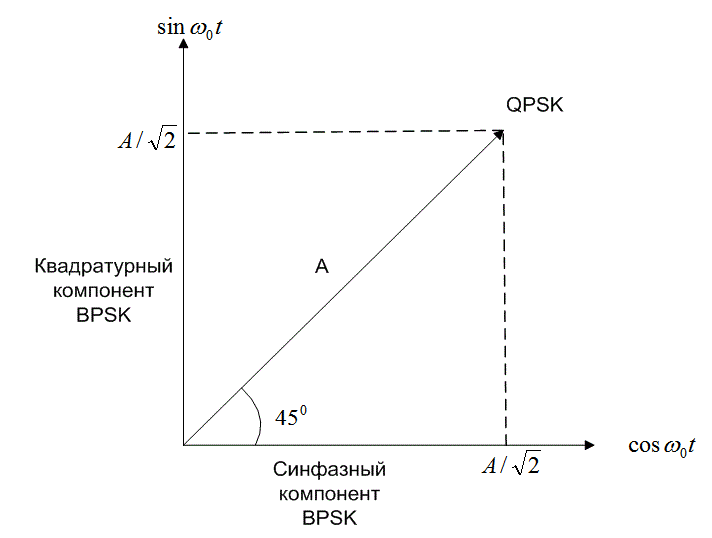
Рис. 4.31. Синфазный и квадратурный компоненты (модуляция BPSK) вектора QPSK

Следовательно, отношение , характеризующее оба ортогональных канала BPSK, создающих сигнал QPSK, эквивалентно отношению в уравнении (4.101), поскольку его можно записать точно так же.

(4.102)

Таким образом, каждый из ортогональных каналов BPSK, а следовательно, и составной сигнал QPSK характеризуются одним отношением , а значит — такой же вероятностью РВ, что и сигнал BPSK. Ортогональность (разность фаз 90°) соседних символов QPSK приводит к равным вероятностям появления ошибочного бита для схем BPSK и QPSK. Следует отметить, что вероятности появления ошибочного символа для этих схем не равны.

4.8.5. Векторное представление сигналов MFSK

В разделе 4.8.3 мы исследовали рис. 4.30, что позволило получить представление о причинах роста вероятности ошибки при увеличении числа k (или М) в схеме MPSK. Полезно будет рассмотреть подобную векторную иллюстрацию для схемы MFSK, которая позволит лучше понять графики на рис. 4.28. Поскольку сигнальное пространство MFSK описывается М взаимно перпендикулярными осями, мы без труда можем проиллюстрировать случаи М = 2 и М = 3. Итак, на рис. 4.32, а видим бинарные ортогональные векторы s1, и s2. Граница областей решений разбивает сигнальное пространство на две области. На рисунке также показан вектор шума n, представляющий минимальный вектор, который может привести к принятию неправильного решения.

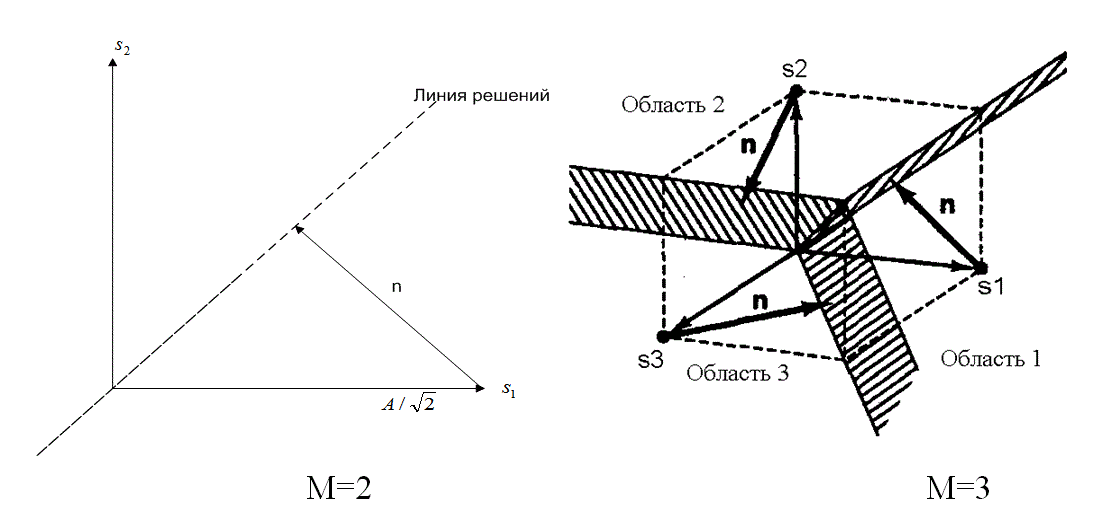
Рис. 4.32. Наборы сигналов MFSK для М = 2,3

На рис. 4.32, б показано трехмерное сигнальное пространство со взаимно перпендикулярными координатными осями. В этом случае плоскости решений разбивают пространство на три области. Показано, как к каждому сигнальному вектору прибавляется вектор шума n, представляющий минимальный вектор, который может привести к принятию неправильного решения. Векторы шума на рис. 4.32, б имеют тот же модуль, что и вектор шума, показанный на рис. 4.32, а. В разделе 4.4.4 мы утверждали, что при данном уровне принятой энергии расстояние между любыми двумя векторами сигналов-прототипов si и sj, М-мерного ортогонального пространства является константой. Отсюда следует, что минимальное расстояние между вектором сигнала-прототипа и любой границей решений не меняется с изменением М. В отличие от модуляции MPSK, когда добавление нового сигнала к сигнальному множеству делало сигналы более уязвимыми к меньшим векторам шума, при MFSK такого не происходит.

Дляиллюстрации этого момента можно было бы нарисовать ортогональные пространства высших размерностей, но, к сожалению, это затруднительно. Мы можем использовать только наш "мысленный взгляд", чтобы понять, что увеличение сигнального множества М — путем введения дополнительных осей, причем каждая новая ось перпендикулярна всем существующим — не приводит к его уплотнению. Следовательно, переданный сигнал, принадлежащий ортогональному набору, не становится более уязвимым к шуму при увеличении размерности. Фактически, как можно видеть из рис. 4.28, 4.28, при увеличении k вероятность появления ошибочного бита даже уменьшается.

Пониманию улучшения надежности при ортогональной передаче сигналов, показанного на рис. 4.28, способствует сравнение зависимости вероятности символьной ошибки (РЕ) от ненормированного отношения сигнал/шум (signal-to-noise ratio — SNR) с зависимостью РЕот еь/nq. На рис. 4.33 для когерентной передачи сигналов FSK представлено несколько зависимостей РЕот нормированного SNR. Видим, что ре падает с ростом М. Можем ли мы сказать, что сигнал из ортогонального набора не становится более уязвимым к данному шуму при увеличении размерности ортогонального набора? Для ортогональной передачи сигналов справедливо утверждение, что при данном SNR вектора шума фиксированного размера достаточно для перевода переданного сигнала в область ошибок; следовательно, сигналы не становятся более уязвимыми к меньшим векторам шума при увеличении М. В то же время при росте М вводится большее число окрестных областей решений; следовательно, увеличивается число возможностей для появления символьной ошибки, всего существует (М- 1) возможностей допустить ошибку. На рис. 4.33 отражено ухудшение РЕв зависимости от ненормированного SNR при увеличении М. Стоит отметить, что изучение зависимости достоверности передачи от М при фиксированном SNR не является лучшим направлением в цифровой связи. Фиксированное SNR означает фиксированный объем энергии на символ; следовательно, при увеличении М этот объем энергии необходимо распределять уже между большим числом битов, т.е. на каждый бит приходится меньше энергии. В этой связи наиболее удобным способом сравнения различных цифровых систем является использование в качестве критерия отношения сигнал/шум, нормированного на бит, или . Повышение достоверности передачи с увеличением М (см. рис. 4.28) проявляется только в том случае, если вероятность ошибки изображается как зависимость от . В этом случае при увеличении М отношение , требуемое для получения заданной вероятности ошибки, снижается при фиксированном SNR; следовательно, нам нужен новый график, подобный показанному на рис. 4.28, где ось абсцисс представляет не SNR, a . На рис. 4.34 показано, как зависимость от SNR отображается в зависимость от ; видно, как графики, демонстрирующие ухудшение РЕс увеличением М (подобно представленному на рис. 4.33), преобразуются в графики, показывающие улучшение РЕс увеличением М. Само преобразование выполняется согласно соотношению, приведенному в формуле (4.101).

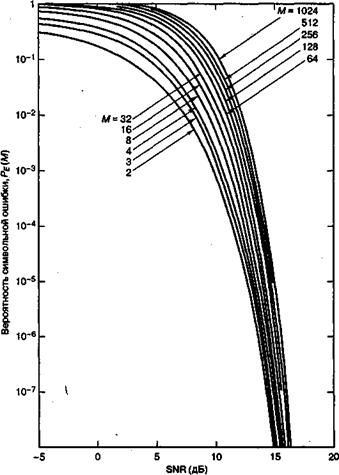
Рис. 4.33. Зависимость вероятности символьной ошибки от SNR для когерентной передани сигналов FSK. (Из документа Bureau of Standards. Technical Note 167, March, 1963; перепечатано с разрешения National Bureau of Standards из Central Radio Propagation Laboratory Technical Note 167, March, 25, 1963, Fig. 1, p. 2.)

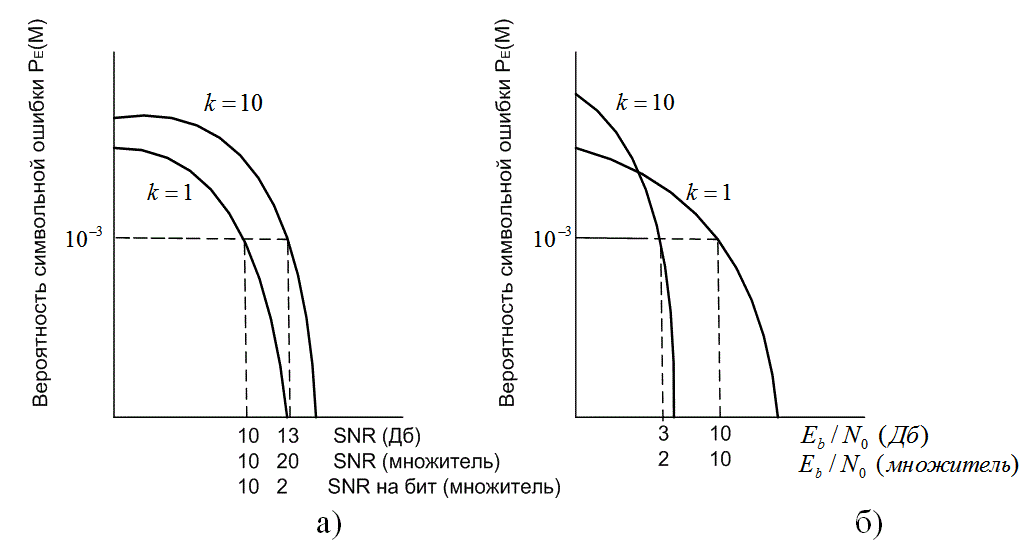
Рис. 4.34. Отображение зависимости PE от SNR в зависимость PE от для ортогональной передачи сигналов: а) ненормированная зависимость; б) нормированная зависимость

Здесь W – ширина полосы обнаружения. Поскольку

где Т – длительность символа, можем записать следующее.

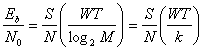(4.103)

При передаче сигналов FSK ширина полосы обнаружения W (в герцах) обычно равна скорости передачи символов 1/Т; другими словами, TW1. Следовательно,

(4.104)

На рис. 4.34 представлено отображение зависимости РЕот SNR в зависимость РЕот для M-мерной ортогональной передачи сигналов с когерентным обнаружением; на осях показано сопоставление величин разных размерностей. На рис. 4.34, а выбрана рабочая точка, соответствующая отношению сигнал/шум = 10 дБ схемы с k= 1, при данной вероятности ошибки РЕ= 10^-3. В той же системе координат приведен график схемы с k= 10; рабочая точка, соответствующая той же величине РЕ= 10^-3, теперь соответствует отношению сигнал/шум, равному 13 дБ (приблизительное значение, полученное из рис. 4.33). Из приведенных графиков явно видно снижение достоверности при увеличении k. Чтобы понять, как улучшается производительность, преобразуем масштаб оси абсцисс из нелинейного (отношение сигнал/шум в децибелах) в линейный (SNR как коэффициент). На рис. 4.34, а показано, как соотносятся значения SNR в децибелах (10 и 13) со значениями, представленными как коэффициент (10 и 20), для случаев k = 1 и k = 10. Далее преобразуем масштаб оси абсцисс, чтобы единицами измерения служило отношение сигнал/шум, нормированное на бит (также выраженное как коэффициент). Этому случаю на рис. 4.34, а соответствуют величины 10 и 2 для k = 1 и k = 10. Вообще, удобно не различать 1024-ричный символ или сигнал (случай k= 10) и его 10-битовое значение. При таком подходе, если символ требует 20 единиц SNR, то 10 бит, кодирующих этот символ, требуют тех же 20 единиц; другими словами, каждый бит требует двух единиц отношения сигнал/шум.

Вместо подобного сравнения, можно просто отобразить рассматриваемые случаи k= 1 и k= 10 графиками, изображенными на рис. 4.34, б и представляющими зависимости РЕот . Случай k= 1 соответствует представленному на рис. 4.34, а. Но для случая k =10 наблюдаем разительные отличия. Видим, что при k=10 передача 10-битового символа требует всего 2 единиц (3 дБ) отношения по сравнению с 10 единицами (10 дБ) для бинарного символа. Действительно, из формулы (4.104) получаем значение отношения = 20 (1/10) = 2 (или 3 дБ), т.е. имеем повышение достоверности при увеличении k. В системах цифровой связи достоверность передачи (или вероятность ошибки) всегда выражается через , поскольку такой подход позволяет выполнять сравнение производительности различных систем. Графики, приведенные на рис. 4.33 и 4.34, а, на практике встречаются крайне редко.

Хотя изображенные на рис. 4.33 зависимости и не используются на практике часто, все же с помощью этого рисунка мы можем понять, почему ортогональная передача сигналов приводит к повышению достоверности при увеличении M или k. Рассмотрим аналогию — приобретение товара, скажем прессованного творога высшего качества. Выбор качества соответствует выбору точки на оси РЕрис. 4.33, скажем 10^-3. Проведем из этой точки горизонтальную линию через все кривые (от M=2 до М = 1024). В бакалейно-гастрономическом отделе мы покупаем самую маленькую упаковку прессованного творога, которая содержит 2 унции и стоит $1. Обращаясь к рис.4.33, можем сказать, что такая покупка соответствует пересечению проведенной горизонтальной линии с графиком для М =2. Смотрим вниз на соответствующее значение параметра SNR и называем пересечение с этой осью ценой $1. При следующем походе за покупками мы решаем, что в прошлый раз стоимость творога была высокой — по 50 центов за унцию. Поэтому решаем купить большую упаковку (8 унций) за $2. Обращаемся к рис.4.33 и видим, что данная покупка соответствует пересечению горизонтальной линии с кривой М = 8. Смотрим вниз и называем соответствующее значение SNR ценой $2. Замечаем, что хотя мы и купили большую емкость, заплатив за нее большую цену, все же стоимость одной унции упала (и составляет теперь всего 25 центов). Эту аналогию можно продолжать; мы можем приобретать все большие и большие упаковки, при этом их цена (SNR) будет расти, а стоимость за унцию будет падать. Вообще, это известно давно и называется эффектом масштаба: приобретение за раз большого количества товара соответствует закупкам по оптовым ценам; при этом цена единицы товара падает. Подобным образом при использовании ортогональной передачи сигналов с символами, содержащими большее число бит, нам требуется большая мощность (большее отношение SNR), а требования относительно бита () при этом снижаются.

4.9. Вероятность символьной ошибки для M-арных систем (М> 2)

4.9.1. Вероятность символьной ошибки для модуляции MPSK

Для больших отношений сигнал/шум вероятность символьной ошибки для равновероятных сигналов в M-арной модуляции PSK с когерентным обнаружением можно выразить как [7]

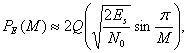(4.105)

где — вероятность символьной ошибки, — энергия, приходящаяся на символ, а М = 2^k — размер множества символов. Зависимость от для передачи сигналов MPSK с когерентным обнаружением показана на рис. 4.35.

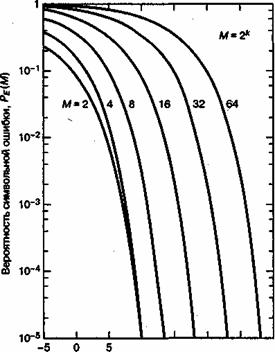
Рис. 4.35. Вероятность символьной ошибки для многофазной передачи сигналов с когерентным обнаружением. (Перепечатано с разрешения авторов из W. С. Lindsey and M. К. Simon. Telecommunication Systems Engineering. Prentice-Hall, Inc., Engle-wood Cliffs, N. J., 1973.)

Вероятность символьной ошибки для дифференциального когерентного обнаружения М-арной схемы DPSK (для больших значений ) выражается подобно тому, как это было приведено выше [7].

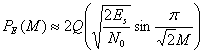(4.106)

4.9.2. Вероятность символьной ошибки для модуляции MFSK

Вероятность символьной ошибки для равновероятных ортогональных сигналов с когерентным обнаружением можно выразить как [5]

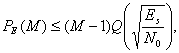(4.107)

где — энергия, приходящаяся на символ, а M — размер множества символов. Зависимость от для М-арных ортогональных сигналов с когерентным обнаружением показана на рис. 4.36.

Вероятность символьной ошибки для равновероятных М-арных ортогональных сигналов с некогерентным обнаружением дается следующим выражением [9].

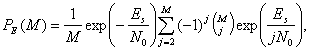(4.108)

где

(4.109)

является стандартным биномиальным коэффициентом, выражающим число способов выбора j ошибочных символов из М возможных. Отметим, что для бинарного случая формула (4. 108) сокращается до

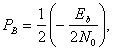(4.110)

что совпадает с результатом, полученным в выражении (4.96). Кривая зависимости от для M-арной передачи сигналов с некогерентным обнаружением изображена на рис. 4.37. При сравнении данных графиков с приведенными на рис. 4.6 и соответствующими когерентному обнаружению можно заметить, что для k > 7 различием уже можно пренебрегать. В заключение отметим, что для когерентного и некогерентного приема ортогональных сигналов верхний предел вероятности ошибки дается выражением [9].

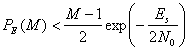(4.111)

Здесь Es — энергия на символ, а М — размер алфавита символов.

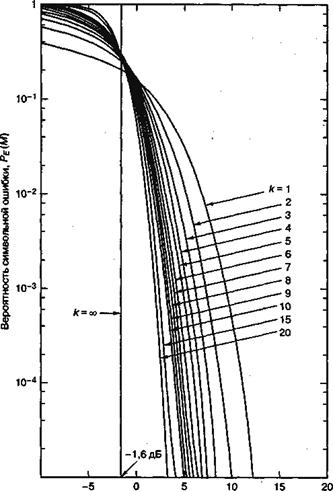
Рис. 4.36. Вероятность символьной ошибки для М-арной ортогональной передачи сигналов с когерентным обнаружением. (Перепечатано с разрешения авторов из W. С. Lindsey and M. К. Simon. Telecommunication Systems Engineering. Prentice-Hall, Inc., Englewood Cliffs, N. J., 1973.)

4.9.3. Зависимость вероятности битовой ошибки от вероятности символьной ошибки для ортогональных сигналов

Можно показать [9], что соотношение между вероятностью битовой ошибки (Р_В) и вероятностью символьной ошибки (Р_Е) для ортогональных M-арных сигналов дается следующим выражением.

                                      (4.112)

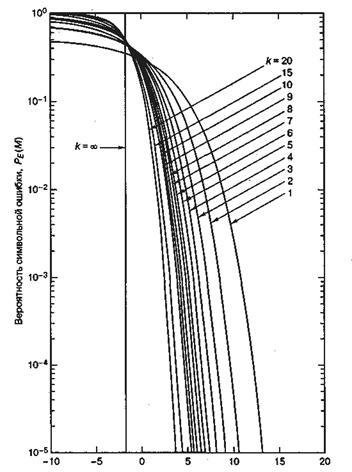
Рис. 4.37. Вероятность символьной ошибки для М-арной ортогональной передачи сигналов с некогерентным обнаружением. (Перепечатано с разрешения авторов из W. С. Lindsey and М. К. Simon, Telecommunication Systems Engineering. Prentice-Hall, Inc., Engtewood Cliffs, N. J., 1973.)

В пределе при увеличении k получаем следующее.

Понять формулу (4.112) позволяет простой пример. На рис. 4.38 показан восьмеричный набор символов сообщения. Эти символы (предполагаемые равновероятными) передаются с помощью ортогональных сигналов, таких как сигналы FSK. При использовании ортогональной передачи ошибка принятия решения равновероятно преобразует верный сигнал в один из (М - 1) неверных. Пример на рисунке демонстрирует передачу символа, состоящего из битов 011. Ошибка с равной вероятностью может перевести данный символ в любой из оставшихся 2^k- 1 = 7 символов. Отметим, что наличие ошибки еще не означает, что все биты символа являются ошибочными. Если (рис. 4.38) приемник решит, что переданным символом является нижний из указанных, состоящий из битов 111, два из трех переданных битов будут верными. Должно быть очевидно, что для недвоичной передачи Р_Ввсегда будет меньше Р_Е (Р_B и Р_Е — средние частоты появления ошибок).

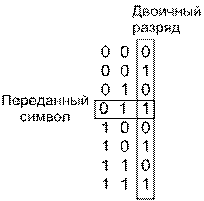
Рис. 4.38. Пример зависимости рв от ре

Рассмотрим любой из столбцов битов на рис. 4.38. Каждая битовая позиция на 50% заполнена нулями и на 50% — единицами. Рассмотрим первый бит переданного символа (правый столбец). Сколько существует возможностей появления ошибочного бита 1? Всего существует 2^k- 1 =4 возможности (нули в столбце появляются в четырех местах) появления битовой ошибки; то же значение получаем для каждого столбца. Окончательное соотношение рв/ре Для ортогональной передачи сигналов в формуле (4.112) получается следующим образом: число возможностей появления битовой ошибки (2^k-1) делится на число возможностей появления символьной ошибки (2^k- 1). Для случая, изображенного на рис. 4.38, .

4.9.4. Зависимость вероятности битовой ошибки от вероятности символьной ошибки для многофазных сигналов

При передаче сигналов MPSK значение Р_Вменьше или равно Р_Е, так же как и при передаче сигналов MFSK. В то же время имеется и существенное отличие. Для ортогональной передачи сигналов выбор одного из (М- 1) ошибочных символов равновероятен. При передаче в модуляции MPSK каждый сигнальный вектор не является равноудаленным от всех остальных. На рис. 4.39, а показано восьмеричное пространство решений, где области решений обозначены 8-ричными символами в двоичной записи. При передаче символа (011) и появлении в нем ошибки наиболее вероятными являются ближайшие соседние символы, (010) и (100). Вероятность превращения символа (011) вследствие ошибки в символ (111) относительно мала. Если биты распределяются по символам согласно двоичной последовательности, показанной на рис. 4.39, а, то некоторые символьные ошибки всегда будут давать две (или более) битовые ошибки, даже при значительном отношении сигнал/шум.

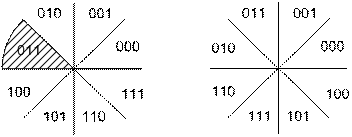
                                            а)                                        б)

Рис. 4.39. Области решения в сигнальном пространстве MPSK: а) в бинарной кодировке; 6) в кодировке Грея

Для неортогональных схем, таких как MPSK, часто используется код преобразования бинарных символов в M-арные, такие, что двоичные последовательности, соответствующие соседним символам (сдвигам фаз), отличаются единственной битовой позицией; таким образом, при появлении ошибки в М-арном символе высока вероятность того, что ошибочным является только один из k прибывших битов. Кодом, обеспечивающим подобное свойство, является код Грея (Gray code) [7]; на рис/4.39, б для восьмеричной схемы PSK показано распределение битов по символам с использованием кода Грея. Можно видеть, что соседние символы отличаются одним двоичным разрядом. Следовательно, вероятность появления многобитовой ошибки при данной символьной ошибке значительно меньше по сравнению с некодированным распределением битов, показанным на рис. 4.39, а. Реализация подобного кода Грея представляет один из редких случаев в цифровой связи, когда определенная выгода может быть получена без сопутствующих недостатков. Код Грея — это просто присвоение, не требующее специальных или дополнительных схем. Можно показать [5], что при использовании кода Грея вероятность ошибки будет следующей.

                                  (4.113)

Напомним из раздела 4.8.4, что передача сигналов BPSK и QPSK имеет одинаковую вероятность битовой ошибки. Формула (4.113) доказывает, что вероятности символьных ошибок этих схем отличаются. Для модуляции BPSK Р_Е = Р_В, а для QPSK Р_Е  2Р_В. Точное аналитическое выражение вероятности битовой ошибки Р_B в восьмеричной схеме PSK, а также довольно точные аппроксимации верхнего и нижнего пределов Р_B для M-арной PSK при больших М можно найти в работе [10].

4.9.5. Влияние межсимвольной интерференции

Обнаружение сигналов рассматривалось при наличии шума AWGN в предположении, что межсимвольная интерференция (intersymbol interference — ISI) отсутствует. Это упростило анализ, поскольку процесс AWGN с нулевым средним описывается единственным параметром — дисперсией. На практике обычно оказывается, что межсимвольная интерференция — это второй (после теплового шума) источник помех, которому необходимо уделять пристальное внимание. ISI может возникать вследствие использования узкополосных фильтров на выходе передатчика, в канале или на входе приемника. Результатом этой дополнительной интерференции является ухудшение достоверности передачи как для когерентного, так и некогерентного приема. Вычисление вероятности ошибки при ISI (помимо AWGN) является значительно более сложной задачей, поскольку в вычислениях будет фигурировать импульсная характеристика канала. Этот вопрос мы не рассматриваем; впрочем, для читателей, интересующихся данной темой, можно порекомендовать работы [11-16].

Литература

1.    Schwartz M. Information, Transmission, Modulation, and Noise. McGraw-Hill Book Company, New York, 1970.

2.    Van Trees H. L. Detection, Estimation, and Modulation Theory. Part 1, John Wiley & Sons, Inc., New York, 1968.

3.    Park J. H., Jr. On Binary DPSK Detection. IEEE Trans. Commun., vol. COM26, n. 4, April, 1978, pp.484-486.

4.    Ziemer R. E. and Peterson R. L. Digital Communications and Spread Spectrum systems. Macmillan-Publishing Company, Inc., New York, 1985.

5.    Lindsey W. C. and Simon M. K.  Telecommunication Systems Engineering. Prentice-Hall,  Inc. Englewood Cliffs, N. J., 1973.

6.    Whalen A. D. Detection of Signals in Noise. Academic Press, Inc., New York, 1971.

7.    Korn I. Digital Communications. Van Nostrand Reinhold Company, Inc., New York, 1985.

8.    Couch L. W. II. Digital and Analog Communication Systems. Macmillan Publishing Company, New York, 1983.

9.   Viterbi A. J. Principles of Coherent Communications. McGraw-Hill Book Company, New York, 1966.

10.  Lee P. J. Computation of the Bit Error Rate of Coherent M-ary PSK with Gray Code Bit Mapping. IEEE Trans. Commun., vol. COM34, n. 5, May, 1986, pp. 488-491.

11.  Hoo E. Y. and Yeh Y. S. A New Approach for Evaluating the Error Probability in the Presence of the Intersymbol Interference and Additive Gaussian Noise. Bell Syst. Tech. J., vol. 49, November, 1970, pp. 2249-2266.

12.  Shimbo O., Fang R. J. and Celebiler M. Performance of M-ary PSK Systems on Gaussian Noise and Intersymbol Interference. IEEE Trans. Inf. Theory, vol. IT19, January, 1973, pp. 44-58.

13.  Prabhu V. K. Error Probability Performance of M-ary CPSK Systems with Intersymbol Interference. IEEE Trans. Commun., vol. COM21, February, 1973, pp. 97-109.

14.  Yao K. and Tobin R. M. Moment Space Upper and Lower Error Bounds for Digital Systems with Intersymbol Interference. IEEE Trans. Inf. Theory, vol. IT22, January, 1976, pp. 65-74.

15.  King M. A., Jr. Three Dimensional Geometric Moment Bounding Techniques. J. Franklin Inst., vol. 309, n. 4, April, 1980, pp. 195-213.

16.  Prabhu V. K. and Salz J. On the Performance of Phase-Shift Keying Systems. Bell Syst. Tech. J., vol. 60, December, 1981, pp. 2307-2343.

Задачи

4.1. Определите точное число битовых ошибок, сделанных за сутки когерентным приемником, использующим схему BPSK. Скорость передачи данных равна 5000 бит/с. Входящими цифровыми сигналами являются: и , где А = 1 мВ, а односторонняя спектральная плотность мощности шума равна Вт/Гц. Считайте, что мощность сигнала и энергия, приходящаяся на бит, нормированы на нагрузку с сопротивлением 1 Ом.

4.2. Непрерывно работающая когерентная система BPSK совершает ошибки со средней частотой 100 ошибок в сутки. Скорость передачи данных 1000 бит/с. Односторонняя спектральная плотность мощности равна Вт/Гц.

а) Чему равна средняя вероятность ошибки, если система является эргодической?

б) Если значение средней мощности принятого сигнала равно 10^-6 Вт, будет ли ее достаточно для поддержания вероятности ошибки, найденной в п. а?

4.3. Если основным критерием производительности системы является вероятность битовой ошибки, какую из следующих двух схем следует выбрать для канала с шумом AWGN? Приведите соответствующие вычисления.

Бинарная некогерентная ортогональная схема FSK с = 13 дБ Бинарная когерентная схема PSK с = 8 дБ

4.4. Поток битов

101010111101010100001111

передается с использованием 'модуляции DPSK. Покажите четыре различные дифференциально-кодированные последовательности, которые могут представлять данное сообщение, и объясните алгоритм генерации каждой из них.

4.5. а) Вычислите минимальную требуемую полосу для некогерентного обнаружения символов в ортогональной бинарной модуляции FSK. Сигнальный тон наивысшей частоты равен 1 МГц, а длительность символа равна 1 мс.

б) Чему равна минимальная требуемая полоса для некогерентной системы MFSK с той же продолжительностью символа?

4.6. Рассмотрим систему BPSK с равновероятными сигналами и . Будем считать, что отношение сигнал/шум в приемнике равно = 9,6 и при идеальной синхронизации вероятность битовой ошибки равна 10^-5. Допустим, восстановление несущей с использованием контура ФАПЧ вносит некоторую фиксированную ошибку φ, связанную с оценкой фазы, так что опорные сигналы выражаются как и . Отметим, что эффект ухудшения достоверности вследствие известного фиксированного смещения можно вычислить, используя аналитические выражения, данные в тексте главы. В то же время, если ошибка фазы будет включать случайное смешение, вычисление его воздействия потребует стохастического рассмотрения (см. главу 10).

а) Насколько возрастет вероятность битовой ошибки при φ = 25°?

б) Какая ошибка в определении фазы приведет к росту вероятности битовой ошибки до 10^-3?

4.7. Определите вероятность появления ошибочного бита РB для когерентного обнаружения с использованием согласованного фильтра равновероятных сигналов FSK.

и

Здесь двусторонняя спектральная плотность мощности шума AWGN равна N0/2= 0,0001. Длительность символа считать равной T =0,01 с.

4.8. Определите оптимальный (дающий минимальную вероятность ошибки) порог у0 для обнаружения равновероятных сигналов и в шуме AWGN при использовании корреляционного приемника, изображенного на рис. 4.7, б. В качестве опорного возьмите сигнал .

4.9. Система обнаружения с помощью согласованного фильтра равновероятных сигналов и работает при шуме AWGN при

отношении Eb/N0 = 6,8 дБ. Считать, что

а) Найдите минимальную вероятность ошибки РB для данного отношения Eb/N0 и данного множества сигналов.

б) Найдите РB, если порог принятия решения равен

в) Порог является оптимальным для определенного множества априорных вероятностей P(s1) и Р(s2). Найдите значения этих вероятностей (используйте раздел Б.2).

4.10. а) Опишите импульсную характеристику согласованного фильтра, используемого для обнаружения дискретного сигнала, изображенного на рис. 34.1. Какой сигнал на выходе фильтра получится при подаче данного сигнала на вход? Воздействием шума можно пренебречь. Чему равно максимальное значение на выходе?

Рис. 34.1

б) В согласованном фильтре сигнал сворачивается с обращенной во времени функцией сигнала (импульсной характеристикой согласованного фильтра). Свертка еще раз обращает функцию; таким образом, согласованный фильтр выдает корреляцию сигнала и его копии (несмотря на то что работа согласованного фильтра описывается операцией свертки). Предположим, что при реализации согласованного фильтра вы случайно соединили каналы так, что фильтр дает корреляцию сигнала и его обращенной во времени копии. Покажите выход как функцию времени. Чему равно максимальное значение на выходе? Отметим, что при данных условиях максимальное значение на выходе появляется в другой момент времени, чем в п. а.

в) С помощью значений на выходе неверного фильтра, описанного в п. б, по сравнению с корректными значениями из п. а, можно ли найти ключ, который поможет предсказать, появляется ли некоторая последовательность с выхода правильного или неправильного фильтра?

г) Пусть к сигналу добавлен шум. Сравните отношение SNR на выходе коррелятора и устройства свертки. Пусть выход состоит исключительно из шума. Сравните выходы коррелятора и устройства свертки.

264 Глава 4. Полосовая модуляция и демодуляция

4.11. Двоичный источник с равновероятными символами управляет положением коммутатора приемника, работающего в канале с шумом AWGN (рис. 34.2) Двусторонняя спектральная плотность шума равна No/2. Пусть передаются антиподные сигналы длительностью Т секунд с энергией Е Дж. Системная схема синхронизации каждые Т секунд генерирует синхронизирующие импульсы, а скорость передачи двоичного источника равна 1/T бит/с. При нормальной работе ключ находится в положении "вверх", когда двоичный нуль, и в положении "вниз", когда двоичная единица. Предположим, что ключ неисправен. С вероятностью р он переключается в неверном направлении на Г-секундный интервал. Наличие ошибки коммутации в течение каждого интервала не зависит от ошибки коммутации

в любое другое время. Считайте, что .

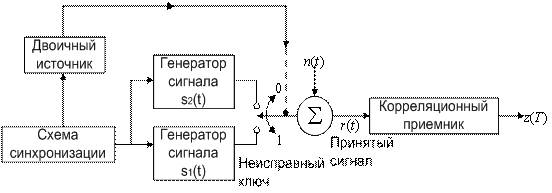
Рис. 34.2

а) Запишите условные вероятности .

б) Корреляционный приемник наблюдает сигнал r(t) в течение интервала (0,T). Нарисуйте блочную диаграмму оптимального приемника для минимизации вероятности битовой ошибки, если известно, что коммутатор сбоит с вероятностью р.

в) Какая система предпочтительнее

или

4.12. а) Рассмотрим систему, использующую 16-ричную модуляцию PSK с вероятностью

символьной ошибки РЕ = 10^-5. При присвоении символам битового значения используется код Грея. Чему приблизительно равна вероятность битовой ошибки?

б) Повторите п. а для 16-ричной ортогональной модуляции FSK.

4.13. Рассмотрим систему ортогональной модуляции MFSK с М = 8; при равновероятных сигналах , где Т= 0,2 мс. Амплитуда несущей, А, равна 1 мВ, а двусторонняя спектральная плотность шума AWGN N0/2 равна 10^-11 Вт/Гц. Вычислите вероятность битовой ошибки, РВ.

4.14. Система со скоростью передачи данных 100 Кбит/с для передачи по каналу с шумом AWGN с использованием модуляции MPSK с когерентным обнаружением требует вероятности битовой ошибки РB = 10^-3. Ширина полосы системы равна 50 кГц. Пусть частотная передаточная функция системы имеет вид приподнятого косинуса с коэффициентом сглаживания r=1 и для присвоения символам битового значения используется код Грея.

а) Чему при заданной РB равно отношение

б) Какое требуется отношение

4.15. Система, использующая дифференциальную модуляцию MPSK и когерентное обнаружение, работает в канале с шумом AWGN при Eb/N0= 10 дБ. Чему равна вероятность символьной ошибки при M = 8 и равновероятных символах?

4.16. Если основным критерием производительности системы является вероятность битовой ошибки, какую из следующих схем модуляции стоит выбрать для передачи по каналу с шумом AWGN?

Когерентная 8-ричная ортогональная FSK с Eb/N0 = 8 дБ или

Когерентная 8-ричная PSK с Eb/N0 =13 дБ

Приведите вычисления. (При присвоении символам битового значения предполагается использование кода Грея.)

4.17. Пусть демодулятор/детектор схемы с модуляцией BPSK содержит ошибку синхронизации, состоящую в смещении времени рТ, где . Другими словами, обнаружение символов начинается и завершается раньше (позже) на время рТ. Предполагается равновероятная передача сигналов и идеальная частотная и фазовая синхронизация. Отметим, что эффект ухудшения достоверности вследствие известного фиксированного смещения можно вычислить, используя аналитические выражения, данные в тексте главы. В то же время, если ошибка фазы будет включать случайное смешение, вычисление его воздействия потребует стохастического рассмотрения (см. главу 10).

а) Выведите выражение для вероятности битовой ошибки РB в зависимости от р.

б) Пусть в приемнике Eb/N0 = 9,6 дБ и р = 0,2; вычислите ухудшение PB в зависимости от смещения времени.

в) Если ошибку, описанную в данном примере, компенсировать не удается, насколько большее отношение Eb/N0 понадобится для восстановления PB, соответствующей p=0?

4.18. Используя все приведенные условия, повторите задачу (4.17) для когерентного обнаружения потока битов в модуляции BFSK.

4.19. Пусть демодулятор/детектор схемы с модуляцией BPSK содержит ошибку синхронизации, состоящую в смещении времени рТ, где . Допустим также, что существует постоянная ошибка оценки фазы φ. Предполагается равновероятная передача сигналов и идеальная частотная синхронизация.

а) Выведите выражение для вероятности битовой ошибки PB в зависимости от p и φ.

б) Пусть в приемнике Eb/N0 = 9,6 дБ, р = 0,2 и φ = 25°; вычислите ухудшение РB в зависимости от смешения времени и фазы.

в) Если ошибки, описанные в данном примере, компенсировать не удается, насколько большее отношение Eb/N0 понадобится для восстановления РB, соответствующей р = 0 и φ = 0°?

4.20. Чаще всего используемым методом синхронизации является корреляция с известной последовательностью Баркера, которая при надлежащей синхронизации дает яркий корреляционный пик, а при ее отсутствии — малый корреляционный выход. С помощью короткой последовательности Баркера 10111 (первым является левый крайний бит) спроектируйте дискретный согласованный фильтр, подобный приведенному на рис. 4.10, который согласовывается с данной последовательностью. Докажите его пригодность, изобразив как функцию времени выход в зависимости от входа, «а который подана последовательность 10111.

Вопросы для самопроверки

4.1. В какой точке системы определяется отношение Eb/N0 (см. раздел 4.3.2)?

4.2. Амплитудная или фазовая манипуляция представляется как совокупность точек или векторов на плоскости. Почему подобное представление нельзя использовать для ортогональной передачи сигналов, например сигналов FSK (см. раздел 4.4.4)?

4.3. Чему при передаче сигналов MFSK равно минимальное расстояние между тонами, обеспечивающее ортогональность сигналов (см. раздел 4.5.4)?

4.4. Какие преимущества при представлении синусоид дает комплексная запись (см. разделы 4.2.1 и 4.6)?

4.5. Схемы цифровой модуляции относятся к одному из двух классов с противоположными поведенческими характеристиками: схемы с ортогональной передачей сигналов и схемы с модуляцией фазы/амплитуды. Опишите поведение каждого класса (см. раздел 4.8.2).

4.6. Почему двоичная фазовая манипуляция (binary phase shift keying — BPSK) и четверичная фазовая манипуляция (quaternary phase shift keying — QPSK) имеют одинаковую вероятность битовой ошибки (см. раздел 4.8.4)?

4.7. Почему при многофазной манипуляции (multiple-phase shift keying — MPSK) эффективность использования полосы повышается с увеличением размерности сигнального пространства (см. разделы 4.8.2 и 4.8.3)?

4.8. Почему при ортогональной передаче, например передаче сигналов MFSK, достоверность передачи повышается с увеличением размерности сигнального пространства (см. раздел 4.8.5)?

4.9. Применение кода Грея является одним из редких случаев в цифровой связи, где определенное преимущество может быть получено безвозмездно. Объясните, почему (см. раздел 4.9.4).