Определим спектры наиболее распространенных типов электрических сигналов.
Единичная функция задается уравнением (7.19) (см. рис. 7.2, а). Строго говоря, функция (7.19) не удовлетворяет условию абсолютной интегрируемости, поэтому воспользуемся следующим приемом: умножим 1(t) на «гасящий» множитель е–ct(с = const). При этом можно использовать прямое преобразование Фурье (9.6):
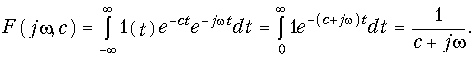
Преобразование F(jw, c) носит название обобщенного преобразования Фурье. Для получения спектра единичной функции перейдем к пределу:
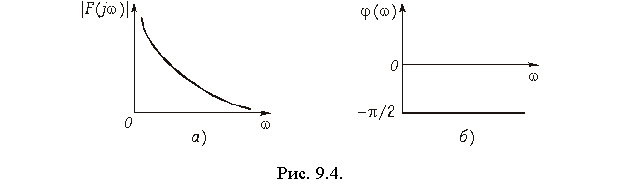
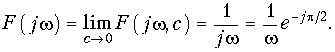
Из уравнения (9.38) получаем амплитудный |F(jw)| = 1/w (рис. 9.4, а) и фазовый спектр функции j(w) (рис. 9.4, б): j(w) = = —p/2, т. е. амплитудный спектр при w = 0 обращается в бесконечность, что свидетельствует о наличии в исходной функции 1(t) скачка при t = 0 (см. рис. 7.2, а). Для образования этого скачка в соответствии с (9.38) при t = 0 осуществляется суммирование бесконечно большого числа синусоидальных составляющих. Спектр (9.38) может быть получен и с помощью изображения единичной функции (7.20):
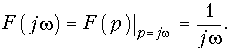
Единичная импульсная функция. Функция d(t) задается аналитически условиями (7.21). Для нахождения спектра d-функции воспользуемся прямым преобразованием Фурье (9.6), которое с учетом (9.8)—(9.10) можно записать в виде
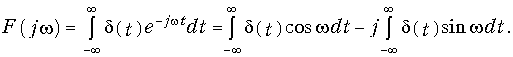
Так как второе слагаемое равно нулю, а первое — единице вследствие свойств (7.21)—(7.23), то окончательно получим
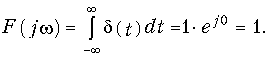
Таким образом, d-функция имеет равномерный амплитудный и нулевой фазовый спектры. Равенство нулю на всех частотах фазового спектра означает, что все гармонические составляющие d-функции, суммируясь с нулевыми начальными фазами, образуют при t = 0 пик бесконечно большого значения.
Следует отметить, что сдвиг d-функции на время t приводит согласно свойствам преобразования Фурье к спектру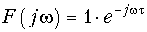 
, т. е. амплитудный спектр функции d(t—t) остается прежним, а фазовый изменяется пропорционально wt.
Из равенства (9.39) согласно обратному преобразованию Фурье (9.7) следует, что
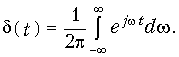
Учитывая условие взаимозаменяемости параметров t и w, последнее выражение можно переписать в следующем виде:
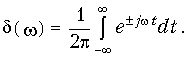
Уравнения (9.40) и (9.41) широко используются в теории сигналов и цепей.
Спектр постоянной составляющей функции a0/2 = 1/2 с учетом (9.41) определяется уравнением
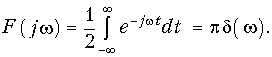
Таким образом, спектр постоянной составляющей равен нулю на всех частотах, кроме w = 0, где F(jw) обращается в бесконечность, то есть имеем на частоте w = 0 дискретную составляющую частоты в форме d-функции.
Спектр гармонического колебания. Проиллюстрируем методику использования прямого преобразования Фурье при определении спектра гармонического колебания
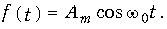
Преобразование (9.6) для функции (9.43) имеет вид
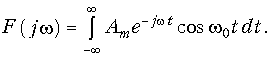
Формально функция (9.43) не удовлетворяет условию абсолютной интегрируемости, так как имеет показатель роста с = 0. По этому для вычисления интеграла (9.44) воспользуемся формулой Эйлера (3.18) и уравнением (9.41):
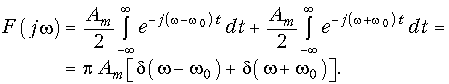
т. е. гармоническое колебание имеет дискретный спектр, состоящий из двух спектральных линий на частотах ±w0.
Спектр одиночного прямоугольного импульса (см. рис. 9.2) можно найти как непосредственно из прямого преобразования Фурье (9.6), так и путем предельного перехода при q ® ¥ (T® ¥) в разложении (5.27). В результате получим
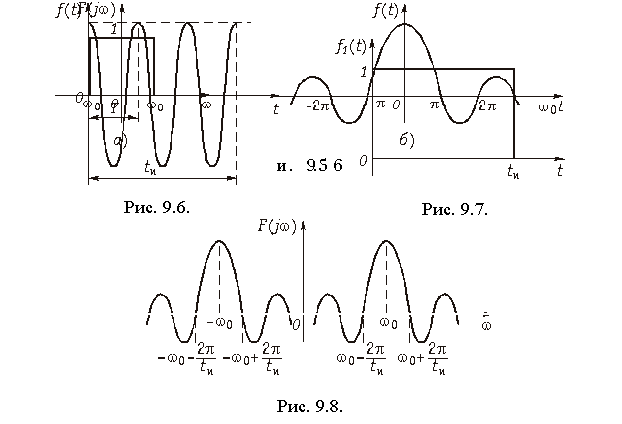
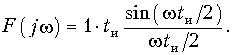
На рис. 9.3 изображен спектр одиночного импульса. Сравнение рис. 9.3 и рис. 9.4 показывает, что по своей форме спектр одиночного импульса совпадает с огибающей дискретного спектра последовательности периодических импульсов, однако спектр одиночного импульса является сплошным.
Из условия взаимосвязи между частотными и временными характеристиками сигнала следует, что сигнал с ограниченным по частоте ±w0 спектром прямоугольной формы (рис. 9.5, а) имеет бесконечную протяженность и форму, аналогичную спектру прямоугольного импульса (рис. 9.5, б).
Спектр радиоимпульса (рис. 9.6) можно найти как произведение видеоимпульса прямоугольной формы (рис. 9.7) и гармонического колебания (9.43). Тогда, воспользовавшись теоремой свертки (9.30), получим:
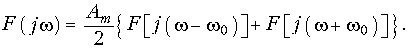
На рис. 9.8 показан вид спектра радиоимпульса.
Аналогичным образом можно найти спектр сигналов и более сложной формы.
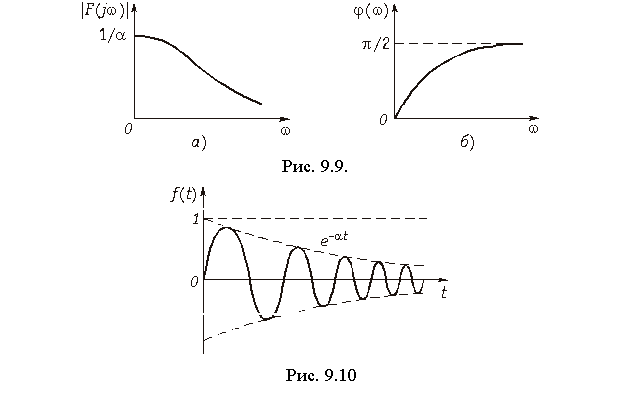
Пример. Найти спектр экспоненциального импульса
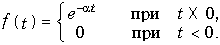
В соответствии с прямым преобразованием (9.6) получаем
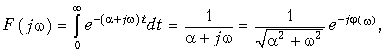
где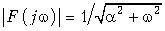 
— амплитудный (рис. 9.9, а) и 
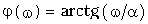—фазовый (рис. 9.9, б) спектры сигнала.
Пример 2. Определить спектр затухающего колебания (рис. 9.10)
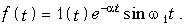
Согласно (9.6) находим
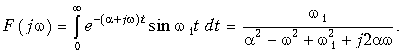
Отсюда находим спектры:
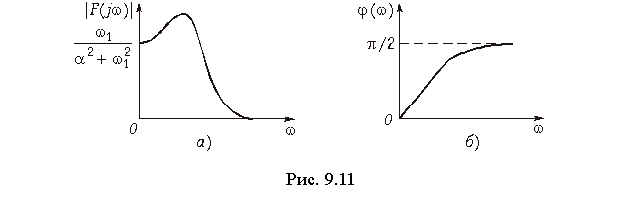
амплитудный (рис. 9.11, а)
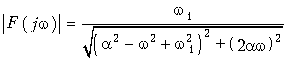
и фазовый (рис. 9.11, б)
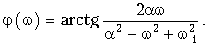
В таблице 9.1 приведены спектры некоторых наиболее распространенных сигналов.