Модовая дисперсия свойственна только многомодовым волокнам и обусловлена отличием времени прохождения мод по ОВ от его входа до выхода. Следует раздельно рассматривать процесс возникновения модовой дисперсии в ступенчатых и градиентных волокнах. В ОВ со ступенчатым профилем показателя преломления скорость распространения электромагнитных волн с длиной волны l одинакова и равна:

, (5.2.1)

где с₀ – скорость света в вакууме.

В этом случае все лучи, падающие на торец ОВ под углами к его оси в пределах апертурного угла q_А (Рисунок 2.7), распространяются в сердцевине волокна по своим зигзагообразным линиям и при одинаковой скорости распространения достигают приемного конца в разное время, что естественно, приводит к увеличению длительности принимаемого импульса.

Увеличение длительности импульса из-за модовой дисперсии характеризуется временем нарастания сигнала и определяется как разность между самым большим и самым малым временем прихода лучей в сечение световода на расстоянии L от начала.

Согласно законам геометрической оптики время распространения луча в ступенчатом многомодовом ОВ зависит от угла падения q_п и, как было показано в [10], определяется выражением:

, (5.2.2)

где:

L – длина световода;

n₁ – показатель преломления сердцевины ОВ;

с₀ – скорость света в вакууме.

Так как минимальное время распространения оптического луча имеет место при q_п=0, а максимальное при q_п=q_кр, соответствующие им значения времени распространения можно записать

и , (5.2.3)

откуда значение межмодовой дисперсии равно

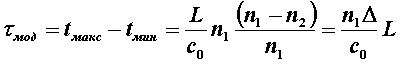. (5.2.4)

Из последнего выражения следует, что модовая дисперсия возрастает с увеличением длины волокна. Однако это справедливо только для идеального волокна, в котором взаимодействие между модами отсутствует. В реальных условиях наличие неоднородностей, кручение и изгиб волокна приводят к постоянным переходам энергии из одних мод в другие то есть к взаимодействию мод, в связи с чем дисперсия становится пропорциональной . Это влияние проявляется не сразу, а после определенного расстояния прохождения световой волны, которое носит название длины установившейся связи мод и принимается равным L_с=(5¸7) км. Оно установлено эмпирическим путем.

Модовая дисперсия градиентных ОВ, как правило, на порядок и более ниже, чем у ступенчатых волокон. Это обусловлено тем, что за счет уменьшения показателя преломления от оси ОВ к оболочке скорость распространения лучей вдоль их траекторий изменяется. Так, на траекториях, близких к оси, она меньше, а удаленных – естественно, больше. Следовательно, лучи, распространяющиеся кратчайшими траекториями (ближе к оси), обладают меньшей скоростью, а лучи, распространяющиеся по более протяженным траекториям, имеют большую скорость. В результате время распространения лучей выравнивается и увеличение длительности импульса становится меньше. При этом время распространения оптических лучей определяется законом изменения показателя преломления и при определенных условиях выравнивается, что, естественно, влечет к уменьшению дисперсии. Так, при параболическом профиле показателя преломления, когда показатель степени в выражении (2.4.2) принимает значение u=2, модовая дисперсия будет определяться выражением

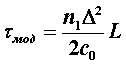. (5.2.5)

При анализе выражений (5.2.4) и (5.2.5) становится очевидным, что модовая дисперсия градиентного ОВ в 2/D раз меньше, чем у ступенчатого при одинаковых значениях D. А так как обычно D»1%, то модовые дисперсии указанных ОВ могут отличаться на два порядка.

В инженерных расчетах при определении модовой дисперсии следует иметь ввиду, что до определенной длины линии L_с, называемой длиной связи мод, нет межмодовой связи, а затем при L>L_с происходит процесс взаимного преобразования мод и наступает установившийся режим. Поэтому при L<L_с дисперсия увеличивается по линейному закону, а затем, при L>L_с, – по квадратичному закону. Следовательно, вышеприведенные формулы расчета модовой дисперсии справедливы лишь для длины линии L<L_с.

При длинах линии L>L_с следует пользоваться следующими формулами:

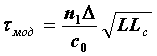		– для ступенчатого световода	(5.2.6)
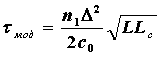		– для градиентного световода,

где L – длина линии; L_с – длина связи мод (установившегося режима), равная 5-7 км для ступенчатого волокна и 10-15 км – для градиентного. Они устанавливаются эмпирическим путем.

Дисперсионные свойства различных типов ОВ, выпускаемых по рекомендациям ITU-TG.651 и G.652, приведены в таблице 5.1. В ступенчатых световодах при многомодовой передаче доминирует модовая дисперсия и она достигает больших значений (20-50нс/км) [10].

Таблица 5.1 – Дисперсионные свойства различных ОВ

Модовая дисперсия может быть уменьшена следующими тремя способами:

- использованием ОВ с меньшим диаметром сердцевины, поддерживающей меньшее количество мод. Например, сердцевина диаметром 50 мкм поддерживает меньшее число мод, чем сердцевина в 100 мкм;

- использованием волокна со сглаженным ППП, чтобы световые лучи, распространяющиеся по более длинным траекториям, имели большую скорость и достигали противоположного конца волокна в тот же момент времени, что и лучи, распространяющиеся по коротким траекториям;

- использованием одномодового волокна, позволяющего избежать модовой дисперсии.