3.4.1. Характеристики канала
Многие каналы связи (например, телефонные или беспроводные) можно охарактеризовать как узкополосные линейные фильтры с импульсной характеристикой ![]() и частотной характеристикой
и частотной характеристикой
![]() (3.82)
(3.82)
где ![]() и
и ![]() - Фурье-образы друг друга,
- Фурье-образы друг друга, ![]() - амплитудная характеристика канала, a
- амплитудная характеристика канала, a ![]() - фазовая характеристика канала.
- фазовая характеристика канала.
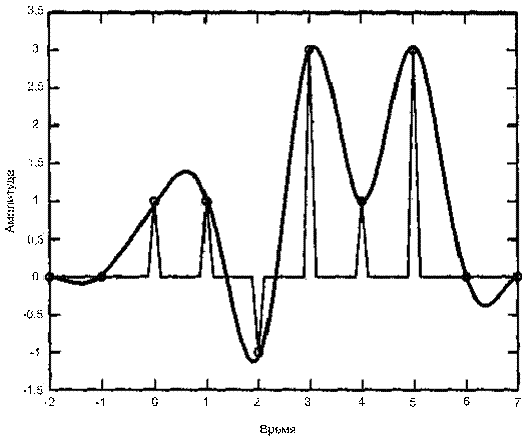
Рис. 3.23, б. Выход фильтра с характеристикой типа приподнятого косинуса и входные дискретные значения, задержанные на некоторое время
В разделе 1.6.3 было показано, что для получения идеальных (неискажающих) передающих характеристик канала в пределах полосы сигнала W, функция ![]() должна быть константой. Кроме того,
должна быть константой. Кроме того, ![]() должна быть линейной функцией частоты, что эквивалентно утверждению «запаздывание должно быть постоянным для всех спектральных компонентов сигнала». Если
должна быть линейной функцией частоты, что эквивалентно утверждению «запаздывание должно быть постоянным для всех спектральных компонентов сигнала». Если ![]() не является константой в пределах полосы W, то канал будет искажать амплитуду сигнала. Если
не является константой в пределах полосы W, то канал будет искажать амплитуду сигнала. Если ![]() не является линейной функцией частоты в пределах полосы W, канал будет искажать фазу. Во многих каналах, искажающих подобным образом информацию, например каналах с замираниями, искажение фазы и амплитуды обычно проявляется одновременно. При передаче последовательности импульсов подобное искажение проявляется в виде рассеивания или «размывания» импульсов, так что ни один импульс принятой демодулированной последовательности не определяется однозначно. В разделе 3.3 описывалось перекрытие импульсов, известное как межсимвольная интерференция (intersymbol interference - ISI). Это эффект, который проявляется в большинстве систем модуляции и является одной из основных помех надежной высокоскоростной передачи по узкополосным каналам. Совокупность методов обработки или фильтрации сигнала, направленных на устранение или снижение межсимвольной интерференции, именуется как «выравнивание» (equalization) и рассматривается в данном разделе.
не является линейной функцией частоты в пределах полосы W, канал будет искажать фазу. Во многих каналах, искажающих подобным образом информацию, например каналах с замираниями, искажение фазы и амплитуды обычно проявляется одновременно. При передаче последовательности импульсов подобное искажение проявляется в виде рассеивания или «размывания» импульсов, так что ни один импульс принятой демодулированной последовательности не определяется однозначно. В разделе 3.3 описывалось перекрытие импульсов, известное как межсимвольная интерференция (intersymbol interference - ISI). Это эффект, который проявляется в большинстве систем модуляции и является одной из основных помех надежной высокоскоростной передачи по узкополосным каналам. Совокупность методов обработки или фильтрации сигнала, направленных на устранение или снижение межсимвольной интерференции, именуется как «выравнивание» (equalization) и рассматривается в данном разделе.
На рис. 2.1 выравнивание разбито на две большие категории. Первая категория, оценка последовательности с максимальным правдоподобием (maximum-likelihood sequence estimation - MLSE), подразумевает измерение ![]() с последующей подстройкой приемника под среду передачи. Цель такой подстройки - позволить детектору произвести точную оценку демодулированной искаженной последовательности импульсов. При использовании приемника MLSE искаженные выборки не изменяются и не проходят этап непосредственной компенсации последствий помех; вместо этого приемник перенастраивается так, чтобы максимально эффективно работать с искаженными выборками. (Пример этого метода, известный как выравнивание Витерби, рассмотрен в разделе 15.7.1.) Вторая категория, выравнивание с помощью фильтров, включает использование фильтров для компенсации искажения импульсов. В этом случае детектору предоставляется последовательность демодулированных выборок, модифицированных или «очищенных» эквалайзером от последствий ISI. Выравнивание с помощью фильтров (более популярный подход из двух описанных выше) также имеет несколько подтипов. Фильтры могут быть линейными устройствами, содержащими только элементы с прямой связью (трансверсальные эквалайзеры), или нелинейными, включающими элементы с обратной связью (эквалайзеры с решающей обратной связью). Кроме того, фильтры могут различаться алгоритмом работы, который может быть заданным или адаптивным. Также они могут различаться разрешением или частотой обновления. Если выборки производятся только в пределах символа, т.е. одна выборка на символ, то это символьное разделение. Если каждому символу соответствует несколько выборок, то это фракционное разделение.
с последующей подстройкой приемника под среду передачи. Цель такой подстройки - позволить детектору произвести точную оценку демодулированной искаженной последовательности импульсов. При использовании приемника MLSE искаженные выборки не изменяются и не проходят этап непосредственной компенсации последствий помех; вместо этого приемник перенастраивается так, чтобы максимально эффективно работать с искаженными выборками. (Пример этого метода, известный как выравнивание Витерби, рассмотрен в разделе 15.7.1.) Вторая категория, выравнивание с помощью фильтров, включает использование фильтров для компенсации искажения импульсов. В этом случае детектору предоставляется последовательность демодулированных выборок, модифицированных или «очищенных» эквалайзером от последствий ISI. Выравнивание с помощью фильтров (более популярный подход из двух описанных выше) также имеет несколько подтипов. Фильтры могут быть линейными устройствами, содержащими только элементы с прямой связью (трансверсальные эквалайзеры), или нелинейными, включающими элементы с обратной связью (эквалайзеры с решающей обратной связью). Кроме того, фильтры могут различаться алгоритмом работы, который может быть заданным или адаптивным. Также они могут различаться разрешением или частотой обновления. Если выборки производятся только в пределах символа, т.е. одна выборка на символ, то это символьное разделение. Если каждому символу соответствует несколько выборок, то это фракционное разделение.
Модифицируем уравнение (3.77), заменив принимающий/ выравнивающий фильтр отдельными (принимающим и выравнивающим) фильтрами, определяемыми частотными передаточными функциями ![]() и
и ![]() . Будем также считать, что общая передаточная функция системы
. Будем также считать, что общая передаточная функция системы ![]() имеет вид приподнятого косинуса (raised-cosine), и обозначим ее
имеет вид приподнятого косинуса (raised-cosine), и обозначим ее ![]() . Таким образом, можем записать следующее.
. Таким образом, можем записать следующее.
![]() (3.83)
(3.83)
В системах, представляющих практический интерес, частотная передаточная функция системы ![]() и ее импульсная характеристика
и ее импульсная характеристика ![]() не известны с точностью, достаточной для разработки приемника, который в любой момент времени дает нулевую межсимвольную интерференцию. Передающий и принимающий фильтры, как правило, выбираются так, чтобы
не известны с точностью, достаточной для разработки приемника, который в любой момент времени дает нулевую межсимвольную интерференцию. Передающий и принимающий фильтры, как правило, выбираются так, чтобы
![]() (3.84)
(3.84)
Таким образом, характеристики ![]() и
и ![]() имеют вид корней из приподнятого косинуса. Следовательно, передаточная функция эквалайзера, необходимая для компенсации искажения, внесенного каналом, является обратной передаточной функции канала.
имеют вид корней из приподнятого косинуса. Следовательно, передаточная функция эквалайзера, необходимая для компенсации искажения, внесенного каналом, является обратной передаточной функции канала.
![]() (3.85)
(3.85)
Иногда частотная передаточная функция системы допускает мёжсимвольную интерференцию в специально выбранных точках дискретизации (например, передаточная функция гауссового фильтра). Такие передаточные функции позволяют повысить эффективность использования полосы, по сравнению с фильтром с характеристикой типа приподнятого косинуса. При выборе такого конструкторского решения выравнивающий фильтр должен компенсировать не только внесенную каналом межсимвольную интерференцию, но и ISI, внесенную передающим и принимающим фильтрами [7].
3.4.2. Глазковая диаграмма
Глазковая диаграмма - это изображение, полученное в результате измерения отклика системы на заданные узкополосные сигналы. На вертикальные пластины осциллографа подается отклик приемника на случайную последовательность импульса, а на горизонтальные - пилообразный сигнал сигнальной частоты. Другими словами, горизонтальная временная развертка осциллографа устанавливается равной длительности символа (импульса). В течение каждого сигнального промежутка очередной сигнал накладывается на семейство кривых в интервале ![]() . На рис. 3.24 приведена глазковая диаграмма, получаемая при двоичной антиподной (биполярные импульсы) передаче сигналов. Поскольку символы поступают из случайного источника, они могут быть как положительными, так и отрицательными, и отображение послесвечения электронного луча позволяет видеть изображение, имеющее форму глаза. Ширина открытия глаза указывает время, в течение которого должна быть произведена выборка сигнала. Разумеется, оптимальное время взятия выборки соответствует максимально распахнутому глазу, что дает максимальную защиту от воздействия помех. Если в системе не используется фильтрация, т.е. если передаваемым информационным импульсам соответствует бесконечная полоса, то отклик системы дает импульсы идеальной прямоугольной формы. В этом случае диаграмма будет выглядеть уже не как глаз, а как прямоугольник. Диапазон разностей амплитуд, обозначенный через
. На рис. 3.24 приведена глазковая диаграмма, получаемая при двоичной антиподной (биполярные импульсы) передаче сигналов. Поскольку символы поступают из случайного источника, они могут быть как положительными, так и отрицательными, и отображение послесвечения электронного луча позволяет видеть изображение, имеющее форму глаза. Ширина открытия глаза указывает время, в течение которого должна быть произведена выборка сигнала. Разумеется, оптимальное время взятия выборки соответствует максимально распахнутому глазу, что дает максимальную защиту от воздействия помех. Если в системе не используется фильтрация, т.е. если передаваемым информационным импульсам соответствует бесконечная полоса, то отклик системы дает импульсы идеальной прямоугольной формы. В этом случае диаграмма будет выглядеть уже не как глаз, а как прямоугольник. Диапазон разностей амплитуд, обозначенный через ![]() , является мерой искажения, вызванного межсимвольной интерференцией, а диапазон разностей времен перехода через нуль, обозначенный через
, является мерой искажения, вызванного межсимвольной интерференцией, а диапазон разностей времен перехода через нуль, обозначенный через ![]() , есть мерой неустойчивой синхронизации. На рисунке также показана мера запаса помехоустойчивости
, есть мерой неустойчивой синхронизации. На рисунке также показана мера запаса помехоустойчивости ![]() и чувствительность к ошибкам синхронизации
и чувствительность к ошибкам синхронизации ![]() . Чаще всего глазковая диаграмма используется для качественной оценки степени межсимвольной интерференции. По мере закрытия глаза ISI увеличивается, а по мере открытия - уменьшается.
. Чаще всего глазковая диаграмма используется для качественной оценки степени межсимвольной интерференции. По мере закрытия глаза ISI увеличивается, а по мере открытия - уменьшается.
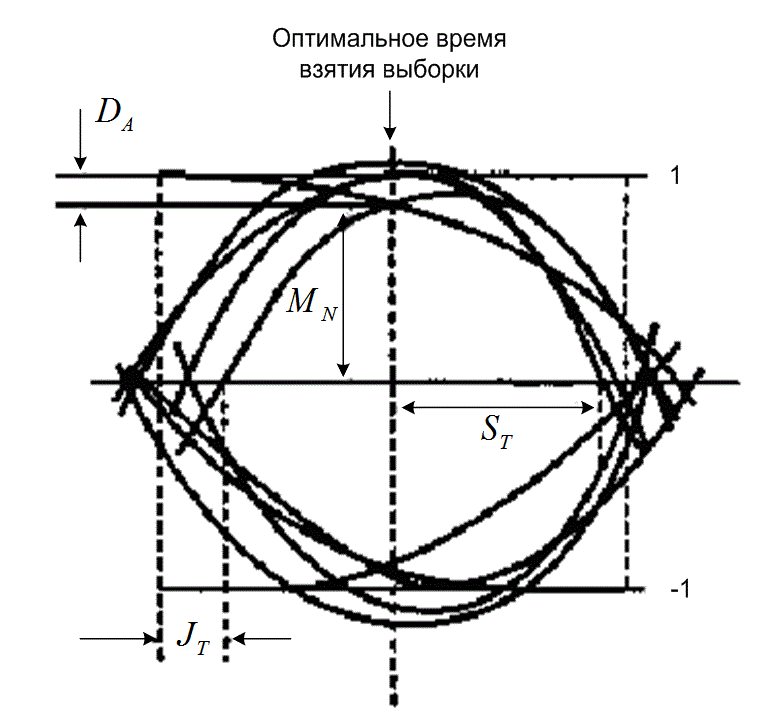
Рис. 3.24. Глазковая диаграмма
3.4.3. Типы эквалайзеров
3.4.3.1. Трансверсальный эквалайзер
В качестве тестовой последовательности, используемой для выравнивания, часто выбирается шумоподобная последовательность с широкополосным спектром, с помощью которой оценивается отклик канала. В простейшем смысле настройка может заключаться в передаче простого короткого импульса (приблизительно, идеального импульса) с последующим изучением импульсного отклика канала. На практике в качестве тестовой последовательности предпочтителен не единичный импульс, а псевдошумовой сигнал, поскольку последний имеет большую среднюю мощность, а значит, большее отношение сигнал/шум при одинаковых максимальных переданных мощностях. Для изучения трансверсального фильтра предположим, что через систему был передан единственный импульс, причем система спроектирована таким образом, что общая передаточная функция имеет вид приподнятого косинуса ![]() . Также будем считать, что канал вводит межсимвольную интерференцию, так что принятый демодулированный импульс искажается, как показано на рис. 3.25, поэтому боковые лепестки, ближайшие к главному лепестку импульса, не проходят через нуль в моменты взятия выборок. Искажение можно рассматривать как положительное или отрицательное отражение, появляющееся до и после главного лепестка. Для получения желаемой передаточной функции с характеристикой типа приподнятого косинуса выравнивающий фильтр, как следует из уравнения (3.85), должен иметь частотный отклик
. Также будем считать, что канал вводит межсимвольную интерференцию, так что принятый демодулированный импульс искажается, как показано на рис. 3.25, поэтому боковые лепестки, ближайшие к главному лепестку импульса, не проходят через нуль в моменты взятия выборок. Искажение можно рассматривать как положительное или отрицательное отражение, появляющееся до и после главного лепестка. Для получения желаемой передаточной функции с характеристикой типа приподнятого косинуса выравнивающий фильтр, как следует из уравнения (3.85), должен иметь частотный отклик ![]() , тогда отклик канала при умножении на
, тогда отклик канала при умножении на ![]() будет
будет ![]() . Другими словами, мы хотим, чтобы выравнивающий фильтр вырабатывал набор подавляющих отражений. Поскольку нас интересуют выборки выровненного сигнала только в определенные моменты времени, проектирование подобного выравнивающего фильтра может быть довольно простой задачей.
. Другими словами, мы хотим, чтобы выравнивающий фильтр вырабатывал набор подавляющих отражений. Поскольку нас интересуют выборки выровненного сигнала только в определенные моменты времени, проектирование подобного выравнивающего фильтра может быть довольно простой задачей.
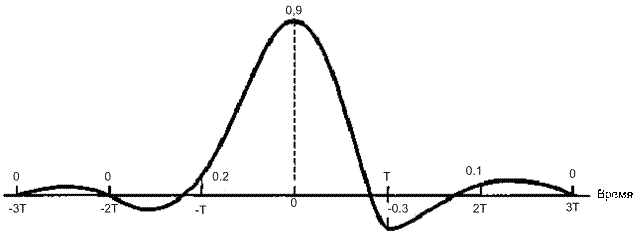
Рис. 3.25. Принятый искаженный импульс
Трансверсальный фильтр, изображенный на рис. 3.26, - это наиболее популярная форма легко настраиваемого выравнивающего фильтра, состоящего из канала задержки с отводами задержки на Т секунд (где Т - длительность символа). В подобном эквалайзере текущее и предыдущее значения принятого сигнала линейно взвешиваются коэффициентами эквалайзера или весовыми коэффициентами отводов ![]() , а затем суммируются для формирования выхода. Основной вклад вносит центральный отвод; вклады остальных отводов связаны с отражениями основного сигнала в течение последующих (и предыдущих) интервалов Т. Если бы можно было создать фильтр с бесконечным числом отводов, можно было бы так подобрать весовые коэффициенты, чтобы импульсный отклик системы равнялся всегда нулю, за исключением моментов взятия выборок; таким образом
, а затем суммируются для формирования выхода. Основной вклад вносит центральный отвод; вклады остальных отводов связаны с отражениями основного сигнала в течение последующих (и предыдущих) интервалов Т. Если бы можно было создать фильтр с бесконечным числом отводов, можно было бы так подобрать весовые коэффициенты, чтобы импульсный отклик системы равнялся всегда нулю, за исключением моментов взятия выборок; таким образом ![]() была бы точно равна обратной передаточной функции канала в формуле (3.85). Несмотря на то что фильтр с бесконечным числом отводов не относится к числу реализуемых, все же можно создать фильтр, достаточно хорошо аппроксимирующий идеальный случай.
была бы точно равна обратной передаточной функции канала в формуле (3.85). Несмотря на то что фильтр с бесконечным числом отводов не относится к числу реализуемых, все же можно создать фильтр, достаточно хорошо аппроксимирующий идеальный случай.
На рис. 3.26 выходы взвешенных отводов усиливаются, суммируются и подаются на устройство принятия решения. Весовые коэффициенты отводов ![]() должны выбираться так, чтобы вычитать эффекты интерференции из символов, соседствующих во времени с искомым символом. Предположим, что существует
должны выбираться так, чтобы вычитать эффекты интерференции из символов, соседствующих во времени с искомым символом. Предположим, что существует ![]() отводов с весовыми коэффициентами
отводов с весовыми коэффициентами ![]() . Выборки на выходе эквалайзера
. Выборки на выходе эквалайзера ![]() находятся путем следующей свертки выборок на входе
находятся путем следующей свертки выборок на входе ![]() и весовых коэффициентов
и весовых коэффициентов ![]() .
.
![]()
![]()
![]() (3.86)
(3.86)
где ![]() - временные коэффициенты, показанные в круглых скобках. (Время может быть как положительным, так и отрицательным.)
- временные коэффициенты, показанные в круглых скобках. (Время может быть как положительным, так и отрицательным.)
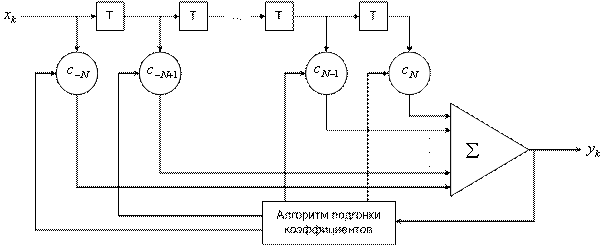
Рис.3.26. Трансверсальный фильтр
Коэффициент ![]() используется для обозначения смещения во времени и как идентификатор коэффициентов фильтра (адрес фильтра). В последнем случае
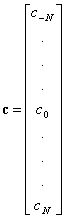
используется для обозначения смещения во времени и как идентификатор коэффициентов фильтра (адрес фильтра). В последнем случае ![]() показан как индекс. Если ввести векторы z и с и матрицу х
показан как индекс. Если ввести векторы z и с и матрицу х
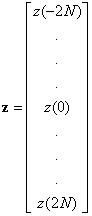
 (3.87)
(3.87)
и
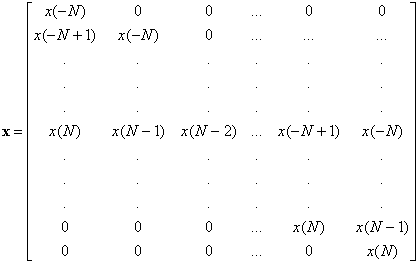 (3.88)
(3.88)
то соотношение между ![]() ,
, ![]() и
и ![]() можно записать в более компактной форме.
можно записать в более компактной форме.
![]() (3.89,а)
(3.89,а)
Если матрица х является квадратной, а число строк и столбцов соответствует числу элементов вектора с, то с можно выразить в следующем виде.
![]() (3.89,б)
(3.89,б)
Отметим, что в общем случае размер вектора z и число строк матрицы х могут быть любыми, поскольку нас может интересовать межсимвольная интерференция в точках взятия выборок, достаточно удаленных от основного лепестка рассматриваемого импульса. В формулах (3.86)-(3.88) индекс k выбирался так, чтобы число точек взятия выборок равнялось ![]() . Векторы z и с имеют размерность
. Векторы z и с имеют размерность ![]() и
и ![]() , соответственно, а матрица х не является квадратной и имеет размер
, соответственно, а матрица х не является квадратной и имеет размер ![]() на
на ![]() . В этом случае система уравнений (3.89,а) называется переопределенной (т.е. число уравнений превышает число неизвестных). Решать подобные уравнения можно с помощью детерминистского способа - метода обращения в нуль незначащих коэффициентов или статистического - метода решения с минимальной среднеквадратической ошибкой (mean-square error - MSE).
. В этом случае система уравнений (3.89,а) называется переопределенной (т.е. число уравнений превышает число неизвестных). Решать подобные уравнения можно с помощью детерминистского способа - метода обращения в нуль незначащих коэффициентов или статистического - метода решения с минимальной среднеквадратической ошибкой (mean-square error - MSE).
Обращение в нуль незначащих коэффициентов
Это решение начинается с отделения N верхних и N нижних строк матрицы х в уравнении (3.88). Таким образом, матрица х становится квадратной размером ![]() на
на ![]() , вектор z также имеет теперь размер
, вектор z также имеет теперь размер ![]() , а формула (3.89,а) определяет детерминированную систему
, а формула (3.89,а) определяет детерминированную систему ![]() уравнений. Предлагаемое решение минимизирует максимальное искажение, вызванное межсимвольной интерференцией, путем выбора весовых коэффициентов
уравнений. Предлагаемое решение минимизирует максимальное искажение, вызванное межсимвольной интерференцией, путем выбора весовых коэффициентов ![]() таким образом, чтобы сигнал на выходе эквалайзера был равен нулю в N точках взятия выборок по обе стороны от искомого импульса. Другими словами, весовые коэффициенты выбираются так, чтобы
таким образом, чтобы сигнал на выходе эквалайзера был равен нулю в N точках взятия выборок по обе стороны от искомого импульса. Другими словами, весовые коэффициенты выбираются так, чтобы
![]()
![]()
![]() (3.90)
(3.90)
Для нахождения ![]() весовых коэффициентов
весовых коэффициентов ![]() из системы
из системы ![]() уравнений используется выражение (3.90). Требуемая длина фильтра (число отводов) зависит от того, насколько сильно канал может «размазать» импульс. Для эквалайзера конечного размера максимальное искажение гарантированно будет минимизировано только в том случае, если глазковая диаграмма изначально имеет вид открытого глаза. В то же время при высокоскоростной передаче и в каналах, вводящих значительную межсимвольную интерференцию, до выравнивания глаз всегда закрыт [8]. Кроме того, эквалайзер, использующий метод обращения в нуль незначащих коэффициентов, не учитывает воздействие шума, поэтому такое решение не всегда является оптимальным.
уравнений используется выражение (3.90). Требуемая длина фильтра (число отводов) зависит от того, насколько сильно канал может «размазать» импульс. Для эквалайзера конечного размера максимальное искажение гарантированно будет минимизировано только в том случае, если глазковая диаграмма изначально имеет вид открытого глаза. В то же время при высокоскоростной передаче и в каналах, вводящих значительную межсимвольную интерференцию, до выравнивания глаз всегда закрыт [8]. Кроме того, эквалайзер, использующий метод обращения в нуль незначащих коэффициентов, не учитывает воздействие шума, поэтому такое решение не всегда является оптимальным.
Пример 3.5. Трехотводный эквалайзер, использующий метод обращения в нуль незначащих коэффициентов
Путем передачи единственного импульса или настроечного сигнала требуется определить весовые коэффициенты отводов выравнивающего трансверсального фильтра. Выравнивающий канал, изображенный на рис. 3.26, состоит всего из трех отводов. Пусть принят искаженный набор выборок импульса ![]() со значениями напряжения 0,0; 0,2; 0,9; -0,3; 0,1, как показано на рис. 3.25. Используйте метод обращения в нуль незначащих коэффициентов для нахождения коэффициентов
со значениями напряжения 0,0; 0,2; 0,9; -0,3; 0,1, как показано на рис. 3.25. Используйте метод обращения в нуль незначащих коэффициентов для нахождения коэффициентов ![]() , уменьшающих межсимвольную интерференцию так, чтобы выборки импульса после выравнивания имели значения
, уменьшающих межсимвольную интерференцию так, чтобы выборки импульса после выравнивания имели значения ![]() . Используя эти весовые коэффициенты, вычислите значения выборок выровненного импульса в моменты
. Используя эти весовые коэффициенты, вычислите значения выборок выровненного импульса в моменты ![]() . Чему равен вклад наибольшей амплитуды в межсимвольную интерференцию и чему равна сумма амплитуд всех вкладов?
. Чему равен вклад наибольшей амплитуды в межсимвольную интерференцию и чему равна сумма амплитуд всех вкладов?
Решение
При заданном импульсном отклике канала из формулы (3.89) получим следующее.
![]()
или
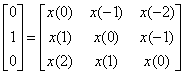
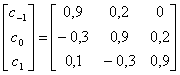
![]()
Решая систему трех уравнений, получаем следующие значения весовых коэффициентов.
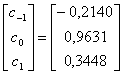
Значения выравненных выборок импульса ![]() , соответствующих временам взятия выборок
, соответствующих временам взятия выборок ![]() вычисляются с помощью формулы (3.89,а).
вычисляются с помощью формулы (3.89,а).
0,0000; -0,0428; 0,0000; 1,0000; 0,0000; -0,0071; 0,0345
Вклад наибольшей амплитуды в межсимвольную интерференцию равен 0,0428, а сумма амплитуд всех вкладов равна 0,0844. Очевидно, что эквалайзер с тремя отводами дает нулевое значение выровненного импульса в точках взятия выборки, соседствующих с основным лепестком. Если создать эквалайзер большего размера, он будет давать нулевое значение в большем числе точек взятия выборок.
Решение с минимальной среднеквадратической ошибкой
Более устойчивый эквалайзер можно получить, выбрав весовые коэффициенты ![]() , минимизирующие среднеквадратическую ошибку (mean-square error - MSE) всех членов, вносящих вклад в межсимвольную интерференцию, плюс мощности шума на выходе эквалайзера [9]. Среднеквадратическая ошибка определяется как математическое ожидание квадрата разности желаемого и обнаруженного информационных символов. Для получения решения с минимальной MSE можно использовать переопределенную систему уравнений (3.89,а), умножив обе ее части на
, минимизирующие среднеквадратическую ошибку (mean-square error - MSE) всех членов, вносящих вклад в межсимвольную интерференцию, плюс мощности шума на выходе эквалайзера [9]. Среднеквадратическая ошибка определяется как математическое ожидание квадрата разности желаемого и обнаруженного информационных символов. Для получения решения с минимальной MSE можно использовать переопределенную систему уравнений (3.89,а), умножив обе ее части на ![]() , что дает [10]
, что дает [10]
![]() (3.91,а)
(3.91,а)
и
![]() , (3.91,б)
, (3.91,б)
где ![]() является вектором взаимной корреляции, a
является вектором взаимной корреляции, a ![]() - автокорреляционной матрицей входного шумового сигнала. На практике
- автокорреляционной матрицей входного шумового сигнала. На практике ![]() и
и ![]() априори неизвестны, но могут быть вычислены приблизительно путем передачи через канал тестового сигнала и использования усреднения по времени для нахождения весовых коэффициентов из уравнения (3.91).
априори неизвестны, но могут быть вычислены приблизительно путем передачи через канал тестового сигнала и использования усреднения по времени для нахождения весовых коэффициентов из уравнения (3.91).
![]() (3.92)
(3.92)
При детерминистском решении метода обращения в нуль незначащих коэффициентов матрица х должна быть квадратной. Но для получения (статистического) решения с минимальной MSE начинать следует с переопределенной системы уравнений, а значит, неквадратной матрицы х, которая впоследствии преобразовывается в квадратную автокорреляционную матрицу ![]() , порождающую систему 2N+1 уравнений, решение которой дает значения весовых коэффициентов, минимизирующих MSE. Размер вектора с и число столбцов матрицы х соответствуют числу отводов выравнивающего фильтра. Большинство высокоскоростных модемов для выбора весовых коэффициентов используют критерий MSE, поскольку он лучше равновесного; он является более устойчивым при наличии шумов и большой межсимвольной интерференции [8].
, порождающую систему 2N+1 уравнений, решение которой дает значения весовых коэффициентов, минимизирующих MSE. Размер вектора с и число столбцов матрицы х соответствуют числу отводов выравнивающего фильтра. Большинство высокоскоростных модемов для выбора весовых коэффициентов используют критерий MSE, поскольку он лучше равновесного; он является более устойчивым при наличии шумов и большой межсимвольной интерференции [8].
Пример 3.6. Семиотводный эквалайзер с минимальной среднеквадратической ошибкой
Путем передачи единственного импульса или настроечного сигнала требуется определить весовые коэффициенты отводов выравнивающего трансверсального фильтра. Выравнивающий канал, изображенный на рис. 3.26, состоит из семи отводов. Пусть принят искаженный набор выборок импульса ![]() со значениями напряжения 0,0108; -0,0558; 0,1617; 1,0000; -0,1749; 0,0227; 0,0110. Используйте решение с минимальной среднеквадратической ошибкой для нахождения весовых коэффициентов
со значениями напряжения 0,0108; -0,0558; 0,1617; 1,0000; -0,1749; 0,0227; 0,0110. Используйте решение с минимальной среднеквадратической ошибкой для нахождения весовых коэффициентов ![]() , минимизирующих межсимвольную интерференцию. Используя эти весовые коэффициенты, вычислите значения выборок выровненного импульса в моменты
, минимизирующих межсимвольную интерференцию. Используя эти весовые коэффициенты, вычислите значения выборок выровненного импульса в моменты ![]() . Чему равен вклад наибольшей амплитуды в межсимвольную интерференцию и чему равна сумма амплитуд всех вкладов?
. Чему равен вклад наибольшей амплитуды в межсимвольную интерференцию и чему равна сумма амплитуд всех вкладов?
Решение
С помощью формулы (3.93) для семиотводного фильтра (N=3), можно записать матрицу х размером 4N+1 на 2N+1=13![]() 7.
7.

Используя матрицу х, можно получить автокорреляционную матрицу ![]() и вектор взаимной корреляции
и вектор взаимной корреляции ![]() , определенные формулами (3.91). С помощью компьютера матрица
, определенные формулами (3.91). С помощью компьютера матрица ![]() обращается, выполняется умножение матриц (см. формулу (3.92)), в результате чего получаются следующие весовые коэффициенты
обращается, выполняется умножение матриц (см. формулу (3.92)), в результате чего получаются следующие весовые коэффициенты ![]() .
.
-0,0116; 0,0108; 0,1659; 0,9495; -0,1318; 0,0670; -0,0269
Подставляя эти весовые коэффициенты в систему уравнений (3.89,а), находим 13 выравненных выборок ![]() в моменты времени
в моменты времени ![]() .
.
-0,0001; -0,0001; 0,0041; 0,0007; 0,0000; 1,0000;
0,0003; -0,0007; 0,0015; -0,0095; 0,0022; -0,0003
Вклад наибольшей амплитуды в межсимвольную интерференцию равен 0,0095, а сумма амплитуд всех вкладов равна 0,0195.
3.4.3.2. Эквалайзер с решающей обратной связью
Основное ограничение линейного эквалайзера, такого как трансверсальный фильтр, заключается в плохой производительности в каналах, имеющих спектральные нули [11]. Подобные каналы часто встречаются в приложениях мобильной радиосвязи. Эквалайзер с решающей обратной связью (decision feedback equalizer - DFE) - это нелинейное устройство, использующее предыдущее решение детектора для устранения межсимвольной интерференции из импульсов, демодулируемых в настоящий момент. Поскольку причиной интерференции являются хвосты предыдущих импульсов, по сути, из текущего импульса вычитается искажение, вызванное предыдущими импульсами.
На рис. 3.27 в виде блочной диаграммы изображен эквалайзер DFE, причем направляющий фильтр и фильтр обратной связи могут быть линейными; например, это может быть трансверсальный фильтр. На рисунке также показано адаптивное обновление весовых коэффициентов фильтра (см. следующий раздел). Нелинейность DFE вытекает из нелинейной характеристики детектора, обеспечивающего подачу сигнала на вход фильтра обратной связи. В основе работы DFE лежит следующее: если значения ранее обнаруженных символов известны (предыдущее решение предполагается точным), то межсимвольную интерференцию, внесенную символами, можно точно уравновесить на выходе направляющего фильтра путем вычитания значений предыдущих символов с соответствующими весовыми коэффициентами. Для удовлетворения выбранного критерия (например, минимальности среднеквадратической ошибки) весовые коэффициенты направляющего отвода и отвода обратной связи могут подгоняться одновременно.
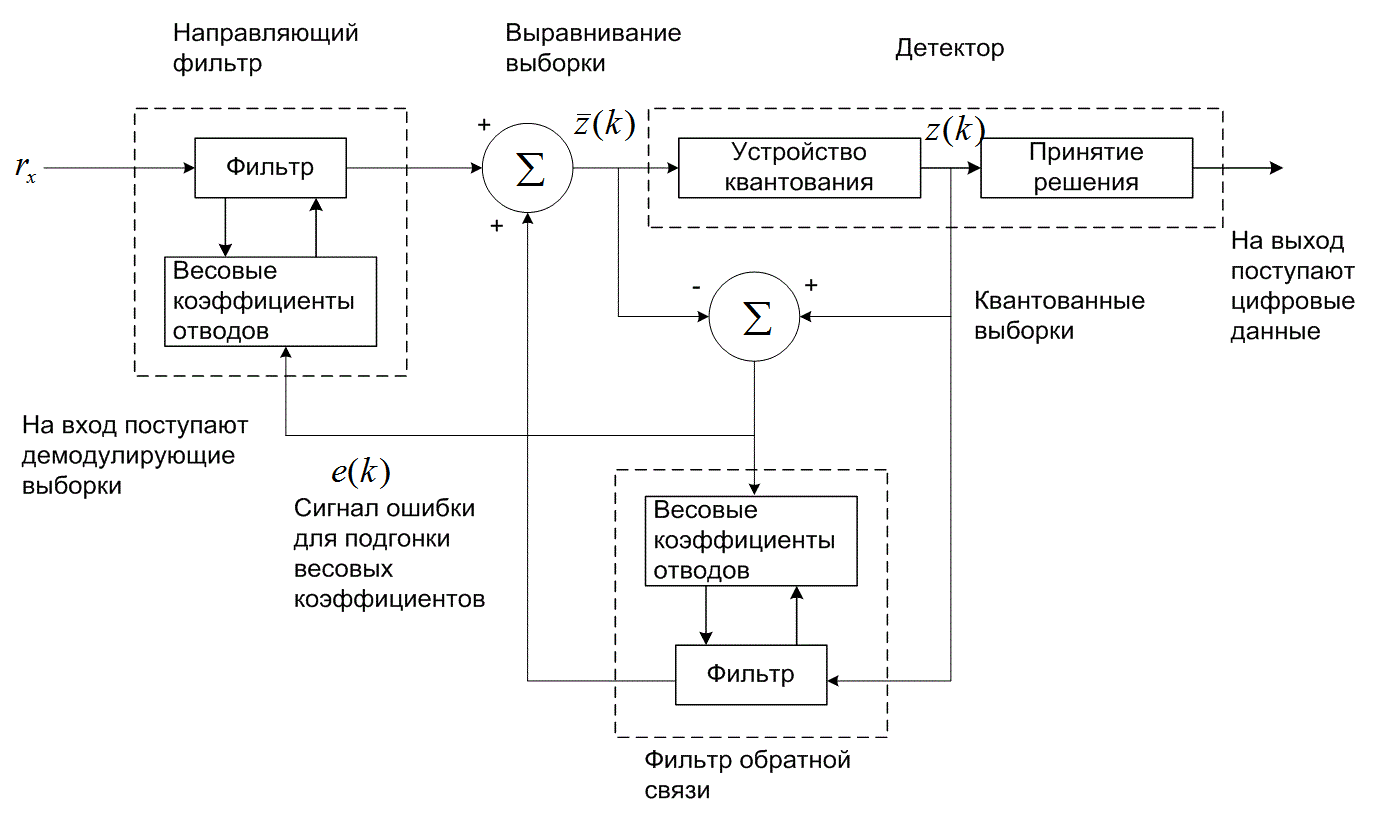
Рис.3.27. Эквалайзер с решающей обратной связью
При использовании единственного направляющего фильтра выход содержит шум канала, внесенный каждой выборкой, произведенной в фильтре. Преимуществом реализации DFE является то, что фильтр обратной связи не только используется для удаления межсимвольной интерференции, но и работает на бесшумных уровнях квантования, а значит на его выходе отсутствует шум канала.
3.4.4. Заданное и адаптивное выравнивание
В инвариантных относительно времени каналах с известными частотными характеристиками, характеристики канала могут измеряться, и, соответственно, могут подгоняться значения весовых коэффициентов отводов. Если весовые коэффициенты остаются фиксированными в течение всего процесса передачи данных, выравнивание называется заданным (preset); простой метод заданного выравнивания заключается в установке весовых коэффициентов ![]() , согласно некоторым усредненным знаниям о канале. Такой метод использовался для передачи информации по телефонным каналам со скоростью, не превышающей 2400 бит/с. Еще один метод заданного выравнивания состоит в передаче настроечной последовательности, которая в приемнике сравнивалась с последовательностью, сгенерированной локально. Отличия последовательностей позволяют установить весовые коэффициенты
, согласно некоторым усредненным знаниям о канале. Такой метод использовался для передачи информации по телефонным каналам со скоростью, не превышающей 2400 бит/с. Еще один метод заданного выравнивания состоит в передаче настроечной последовательности, которая в приемнике сравнивалась с последовательностью, сгенерированной локально. Отличия последовательностей позволяют установить весовые коэффициенты ![]() . Важным моментом использования любой разновидности заданного выравнивания является то, что установка параметров производится либо единожды, либо в исключительно редких случаях (например, при прерывании передачи и необходимости ее повторной настройки).
. Важным моментом использования любой разновидности заданного выравнивания является то, что установка параметров производится либо единожды, либо в исключительно редких случаях (например, при прерывании передачи и необходимости ее повторной настройки).
Тип выравнивания, способный отслеживать постепенные изменения, называется адаптивным (adaptive). Его реализация может включать периодическую или непрерывную «подборку» весовых коэффициентов отводов. Периодическая корректировка выполняется путем периодической передачи начальной комбинации битов или краткой настроечной последовательности, заранее известной приемнику. Кроме того, начальная комбинация битов используется приемником для определения начала передачи, установки уровня автоматической регулировки усиления (automatic gain control - AGC) и для согласования с принятым сигналом внутренних часов и местных гетеродинов. Непрерывная подстройка осуществляется посредством замещения известной тестовой последовательности набором информационных символов, которые получены на выходе эквалайзера и считаются известными данными. При непрерывной и автоматической (наиболее распространенный подход) настройке используется метод, управляемый решением (decision directed) [11]. Название метода не стоит путать с DFE - эквалайзером с решающей обратной связью. Управление решением связано только со способом юстировки (с помощью сигнала от детектора) весовых коэффициентов отводов фильтра. Эквалайзер DFE - это наличие дополнительного фильтра на выходе детектора, рекурсивным образом возвращающего сигнал на вход детектора. Следовательно, при использовании DFE существует два фильтра (направляющий и фильтр обратной связи), обрабатывающие данные для снижения межсимвольной интерференции.
Недостатком заданного выравнивания является то, что оно требует предварительной настройки в начале каждой новой передачи. Кроме того, нестационарные каналы, вследствие межсимвольной интерференции и фиксированных весовых коэффициентах отводов, могут приводить к ухудшению производительности системы. Адаптивное выравнивание, в частности адаптивное выравнивание, управляемое решением, успешно устраняет межсимвольную интерференцию, если первоначальная вероятность ошибки не превышает один процент (эмпирическое правило). Если вероятность ошибки превышает один процент, эквалайзер, управляемый решением, может и не дать требуемого результата. Общее решение этой проблемы - инициализировать эквалайзер с альтернативным процессом, (таким, как передача начальной комбинации битов), что позволит обеспечить низкую вероятность ошибки в канале, а затем переключиться в режим управления решением. Чтобы избежать служебных издержек, вносимых начальной комбинацией битов, проекты многих систем предусматривают работу в режиме непрерывного широковещания с использованием для первоначальной оценки канала алгоритмов слепого выравнивания (blind equalization). Эти алгоритмы согласовывают коэффициенты фильтра со статистикой выборок, а не с решениями относительно значений выборок [11].
Для оценки оптимальных коэффициентов автоматические эквалайзеры используют итеративные методы. Система уравнений, приведенная в выражении (3.93), не учитывает воздействие шума канала. При получении устойчивого решения для значений весовых коэффициентов фильтра, требуется усреднять либо данные для устойчивой статистики сигнала, либо зашумленное решение, полученное из зашумленных данных. Сложность алгоритма и проблемы численной устойчивости часто приводит к разработке алгоритмов, усредняющих зашумленные решения. Наиболее надежным из этого класса алгоритмов является алгоритм минимальной среднеквадратической (least-mean-square - LMS) ошибки. Каждая итерация этого алгоритма использует зашумленную оценку градиента ошибок для регулировки весовых коэффициентов относительно снижения среднеквадратической ошибки. Градиент шума - это просто произведение ![]() скалярного значения ошибки
скалярного значения ошибки ![]() и вектора данных
и вектора данных ![]() . Вектор
. Вектор ![]() - это вектор выборок канала, которые подверглись воздействию шума и в момент k находились на выравнивающем фильтре. Выше использовалось следующее математическое представление: передавался импульс, и выравнивающий фильтр работал с последовательностью выборок (вектором), представляющей импульсный отклик канала. Эти принятые выборки (в виде сдвига во времени) изображались как матрица х. Теперь, вместо использования отклика на импульс, предполагается передача данных на вход фильтра (рис. 3.27), соответственно определяется вектор принятых выборок
- это вектор выборок канала, которые подверглись воздействию шума и в момент k находились на выравнивающем фильтре. Выше использовалось следующее математическое представление: передавался импульс, и выравнивающий фильтр работал с последовательностью выборок (вектором), представляющей импульсный отклик канала. Эти принятые выборки (в виде сдвига во времени) изображались как матрица х. Теперь, вместо использования отклика на импульс, предполагается передача данных на вход фильтра (рис. 3.27), соответственно определяется вектор принятых выборок ![]() , представляющий информационный отклик канала. Ошибка записывается как разность желаемого сигнала и сигнала, полученного на выходе фильтра.
, представляющий информационный отклик канала. Ошибка записывается как разность желаемого сигнала и сигнала, полученного на выходе фильтра.
![]() (3.93)
(3.93)
Здесь ![]() - желаемый выходной сигнал (выборка без межсимвольной интерференции), а
- желаемый выходной сигнал (выборка без межсимвольной интерференции), а ![]() - оценка
- оценка ![]() в момент времени k (производится в устройстве квантования, показанном на рис. 3.27), имеющая следующий вид.
в момент времени k (производится в устройстве квантования, показанном на рис. 3.27), имеющая следующий вид.
![]() (3.94)
(3.94)
В формуле (3.94) суммирование представляет свертку входящих информационных выборок с весовыми коэффициентами отводов ![]() , где
, где ![]() - коэффициент
- коэффициент ![]() -го отвода в момент времени k, а
-го отвода в момент времени k, а ![]() - транспонированный вектор весовых коэффициентов в момент времени k. Далее будет показано, что итеративный процесс, обновляющий значения весовых коэффициентов в каждый момент времени k, имеет следующий вид.
- транспонированный вектор весовых коэффициентов в момент времени k. Далее будет показано, что итеративный процесс, обновляющий значения весовых коэффициентов в каждый момент времени k, имеет следующий вид.
![]() (3.95)
(3.95)
Здесь ![]() - вектор весовых коэффициентов фильтра в момент времени k, а
- вектор весовых коэффициентов фильтра в момент времени k, а ![]() - малый член, ограничивающий шаг коэффициентов, а значит, контролирующий скорость сходимости алгоритма и дисперсию устойчивого решения. Это простое соотношение является следствием принципа ортогональности, утверждающего, что ошибка, сопровождающая оптимальное решение, ортогональна обрабатываемым данным. Поскольку алгоритм рекурсивен (по отношению к весовым коэффициентам), необходимо следить за его устойчивостью. Устойчивость гарантируется, если параметр
- малый член, ограничивающий шаг коэффициентов, а значит, контролирующий скорость сходимости алгоритма и дисперсию устойчивого решения. Это простое соотношение является следствием принципа ортогональности, утверждающего, что ошибка, сопровождающая оптимальное решение, ортогональна обрабатываемым данным. Поскольку алгоритм рекурсивен (по отношению к весовым коэффициентам), необходимо следить за его устойчивостью. Устойчивость гарантируется, если параметр ![]() меньше значения обратной энергии данных в фильтре. Если алгоритм является устойчивым, он в среднем сходится к оптимальному решению, при этом его дисперсия пропорциональна параметру
меньше значения обратной энергии данных в фильтре. Если алгоритм является устойчивым, он в среднем сходится к оптимальному решению, при этом его дисперсия пропорциональна параметру ![]() . Таким образом, желательно, чтобы параметр сходимости
. Таким образом, желательно, чтобы параметр сходимости ![]() был больше (для более быстрой сходимости), но не настолько, чтобы привести к неустойчивости, хотя, с другой стороны, малый параметр
был больше (для более быстрой сходимости), но не настолько, чтобы привести к неустойчивости, хотя, с другой стороны, малый параметр ![]() обеспечивает малую дисперсию. Обычно для получения низкодисперсного устойчивого решения
обеспечивает малую дисперсию. Обычно для получения низкодисперсного устойчивого решения ![]() выбирается равным фиксированной небольшой величине [12]. Существуют схемы [13], позволяющие
выбирается равным фиксированной небольшой величине [12]. Существуют схемы [13], позволяющие ![]() меняться от больших значений к меньшим в процессе получения устойчивого решения.
меняться от больших значений к меньшим в процессе получения устойчивого решения.
Отметим, что уравнения (3.93)-(3.95) приведены в контексте вещественных сигналов. Если используется квадратурная реализация, так что сигнал описывается вещественной и мнимой (или синфазной и квадратурной) упорядоченными парами, то каждый канал на рис. 3.27 в действительности состоит из двух каналов, и уравнения (3.93)-(3.95) необходимо записывать в комплексной форме.
3.4.5. Частота обновления фильтра
Выравнивающие фильтры классифицируются по частоте дискретизации входящего сигнала. Трансверсальный фильтр с отводами, размещенными через Т секунд, где Т - длительность передачи символа, называется эквалайзером с символьным разделением (symbol-spaced equalizer). Процесс дискретизации выхода эквалайзера с частотой ![]() приводит к наложению, если полоса сигнала не ограничена строго величиной
приводит к наложению, если полоса сигнала не ограничена строго величиной ![]() Гц, т.е. спектральные компоненты сигнала, не разделенные промежутком
Гц, т.е. спектральные компоненты сигнала, не разделенные промежутком ![]() Гц, накладываются. Наложенная версия сигнала может давать спектральные нули [8]. Частота обновления фильтра, превышающая скорость передачи символов, помогает смягчить эту проблему. Эквалайзеры, использующие подобный метод, называются эквалайзерами с фракционным разделением (fractionally-spaced equalizer). В таких устройствах отводы фильтра разделены промежутками
Гц, накладываются. Наложенная версия сигнала может давать спектральные нули [8]. Частота обновления фильтра, превышающая скорость передачи символов, помогает смягчить эту проблему. Эквалайзеры, использующие подобный метод, называются эквалайзерами с фракционным разделением (fractionally-spaced equalizer). В таких устройствах отводы фильтра разделены промежутками
![]() секунд, (3.96)
секунд, (3.96)
где через ![]() обозначен избыток полосы. Другими словами, ширина принятого сигнала равна следующему.
обозначен избыток полосы. Другими словами, ширина принятого сигнала равна следующему.
![]() (3.97)
(3.97)
![]() необходимо выбрать так, чтобы передаточная функция эквалайзера
необходимо выбрать так, чтобы передаточная функция эквалайзера ![]() была значительно шире и охватывала весь спектр сигнала. Отметим, что сигнал на выходе эквалайзера по-прежнему выбирается с частотой
была значительно шире и охватывала весь спектр сигнала. Отметим, что сигнал на выходе эквалайзера по-прежнему выбирается с частотой ![]() , но поскольку весовые коэффициенты отводов разделены промежутками
, но поскольку весовые коэффициенты отводов разделены промежутками ![]() (входящий сигнал эквалайзера выбирается с частотой
(входящий сигнал эквалайзера выбирается с частотой ![]() ), выравнивание принятого сигнала происходит до наложения его частотных компонентов. Моделирование эквалайзеров в телефонных линиях с
), выравнивание принятого сигнала происходит до наложения его частотных компонентов. Моделирование эквалайзеров в телефонных линиях с ![]() показывает, что эквалайзеры с фракционным разделением превосходят эквалайзеры с символьным разделением [14].
показывает, что эквалайзеры с фракционным разделением превосходят эквалайзеры с символьным разделением [14].

