9.5.1. Эффективность использования полосы при выборе схем MPSK и MFSK
С помощью уравнения (9.6) можно составить график зависимости нормированной полосы пропускания канала W/C (в Гц/бит/с) от Eb|N0, как показано на рис. 9.4. Здесь в качестве независимой переменной взято Eb|N0 и можно видеть компромисс между активной мощностью и полосой пропускания, так сказать, в деле. Можно показать [5], что качественно спроектированные системы должны стремиться к работе в области излома кривой компромисса между полосой пропускания и мощностью для идеального (R=С) канала. Характеристики реальных систем часто отличаются от идеальных не более чем на 10 дБ. Наличие излома означает, что в системах, в которых предпринимается попытка уменьшить занимаемую полосу пропускания канала или снизить требуемую мощность, приходится все больше повышать значение другого параметра (что является не очень желательным). Например, возвращаясь к рис. 9.4, можно сказать, что идеальная система, работающая при Eb|N0=1,8 дБ и использующая полосу частот с нормированной шириной 0,5 Гц/бит/с, для уменьшения используемой полосы частот до 0,1 Гц/бит/с должна поднять Eb|N0 до 20 дБ. Подобное будет происходить и при попытке компромисса в обратную сторону.
С помощью уравнения (9.6,в) можно также получить зависимость C/W от Eb|N0. Она показана на графике зависимости R/W от Eb|N0 (рис. 9.6). Обозначим эту плоскость как плоскость "полоса-эффективность". Ордината R/W— это мера объема данных, которые можно передать через единицу полосы частот за данное время; следовательно, она отображает эффективность использования ресурса полосы пропускания. Независимая переменная Eb|N0 измеряется в децибелах. На рис. 9.6 кривая R=С - это граница, разделяющая область реальных прикладных систем связи и область, в которой такие системы связи теоретически невозможны. Подобно изображенной на рис. 9.2, характеристика эффективности полосы пропускания на рис. 9.6 устанавливает предельные параметры, которые достижимы для прикладных систем. Поскольку в качестве независимой переменной более предпочтительно Eb|N0, чем SNR, рис. 9.6 удобнее рис. 9.2 с точки зрения сравнения компромиссов кодирования и модуляции в цифровой связи. Отметим, что на рис. 9.6 проиллюстрирована зависимость эффективности использования полосы частот от Eb|N0 для систем с одной несущей. Для систем с множественными несущими эффективность использования полосы частот зависит от разнесения несущих (и типа модуляции). В этом случае компромисс — это насколько разнесены несущие (что приводит к повышению эффективности использования полосы частот) без возникновения неприемлемых помех соседних каналов (adjacent channel interference — ACI).
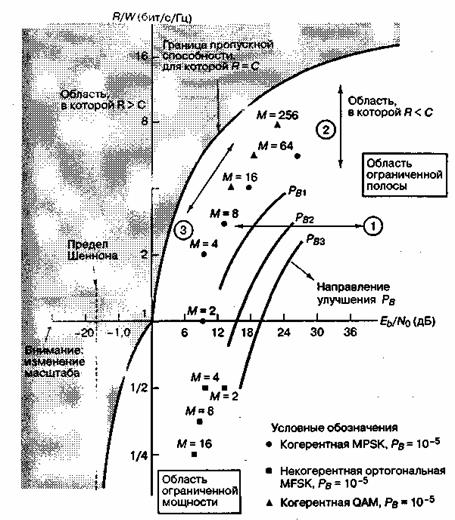
Рис. 9.6. Плоскость «полоса-эффективность».
9.5.1. Эффективность использования полосы при выборе схем MPSK и MFSK
На рис. 9.6 показаны рабочие точки для когерентной модуляции MPSK при вероятно сти битовой ошибки 10-5. Предполагается, что до модуляции осуществляется фильтра ция по Найквисту (идеальная прямоугольная), так что минимальная двойная полоса пропускания на промежуточной частоте (intermediate frequency — IF) WIF = 1/T, где Т -длительность символа. Таким образом, из уравнения (9.1) эффективность использования полосы частот R/W= log2М, где М — размер набора символов. Для реальных каналов и сигналов производительность следует понизить, чтобы учесть увеличение полосы пропускания, требуемое для создания реализуемых фильтров. Отметим, что npи модуляции MPSK RIW растет с увеличением М. Кроме того, положение рабочих точек MPSK указывает, что для модуляции BPSK (М=2) и квадратичной PSK, или QPSK (М=4), требуются одинаковые значения Eb|N0. Иными словами, при том же значенш Eb|N0 эффективность использования полосы частот для схемы QPSK равна 2 бит/с/Гц в отличие от 1 бит/с/Гц для схемы BPSK. Эта уникальная особенность является следcтвием того, что QPSK представляет собой эффективную комбинацию двух сигналов модуляции BPSK, которые передаются на ортогональных компонентах несущей.
На рис. 9.6 также изображены рабочие точки некогерентной ортогональной модуляции MFSK при вероятности появления битовой ошибки 10-5. Предполагается, что полоса передачи равна WIF=M/T. Следовательно (исходя из уравнения (9.1)), эффективность использования полосы частот равна R/W=(log2M)/M. Отметим, что при модуляции MFSK R/W снижается с увеличением М. Также следует отметить, что положение рабочих точек MFSK указывает, что модуляция BFSK (М=2)и квадратичная FSK (М=4) имеют одинаковую эффективность использования полосы частот, хотя первая требует большего значения Eb|N0 для той же вероятности появления ошибки. Эффективность использования полосы частот изменяется с коэффициентом модуляции (разнесение частот в герцах, деленное на скорость передачи битов). Предполагается, что для каждого сигнала, модулированного MFSK, требуется одинаковое приращение полосы пропускания, а значит, при М=2 эффективность использования полосы составляет 1 бит/с/2 Гц или 1/2, а при М=4 RIW — 2 бит/с/4 Гц, или 1/2. Таким образом, двоичная и 4-уровневая ортогональная FSK характеризуются одинаковыми значениями RIW.
На рис. 9.6 также показаны рабочие точки для когерентной квадратурной амплитудной модуляции (quadrature amplitude modulation — QAM). Видно, что на фоне остальных модуляций QAM наиболее эффективно использует полосу частот; к этому типу модуляции мы еще обратимся в разделе 9.8.3.
9.5.2. Аналогия между графиками эффективности использования полосы частот и вероятности появления ошибки
График эффективности использования полосы на рис. 9.6 аналогичен графику вероятности ошибки на рис. 9.1. Предел Шеннона (рис. 9.1) является аналогом предельной пропускной способности (рис. 9.6). Кривые на рис. 9.1 называются кривыми равной полосы пропускания. На рис. 9.6 можно аналогично описать кривые равной вероятности для различных схем кодирования и модуляции. Кривые, обозначенные как PB1, PB2 иPB3 являются гипотетическими конструкциями для некоторых произвольных схем модуляции и кодирования; кривая PB1 представляет собой наибольшую из трех вероятность появления ошибки, а кривая PB3 — наименьшую. Также на рисунке указано направление снижения PB.
Ранее, при изучении графика вероятности появления ошибки, рассматривались возможные компромиссы между PB, Eb|N0 и W. Аналогичные компромиссы можно рассмотреть и на графике эффективности использования полосы частот. Возможные компромиссы отображены на рис. 9.6 как сдвиги рабочей точки в направлениях, указанных стрелками. Сдвиг рабочей точки вдоль линии 1 можно рассматривать как поиск компромиссов между Pb и Eb|N0 при фиксированном значении R/W. Точно так же сдвиг вдоль линии 2 — это поиск компромиссов между Pb и W (или RIW) при фиксированном значении Eb|N0 . И наконец, сдвиг вдоль линии 3 показывает поиск компромиссов между W (или R/W) и Eb|N0 при постоянном значении Pb. На рис. 9.6 (как и на рис. 9.1) сдвиг вдоль линии 1 может быть вызван повышением или снижением номинального Eb|N0. Сдвиги вдоль линии 2 или 3 требуют изменений схемы модуляции или кодирования.
Два основных ресурса связи — это переданная мощность и ширина полосы пропускания. Для разных систем связи один из этих ресурсов дороже другого, и следовательно, большую часть систем можно классифицировать как системы ограниченной мощности или ограниченной полосы пропускания. В системах ограниченной мощности для экономии энергии за счет полосы пропускания можно использовать схемы кодирования, эффективно использующие мощность, тогда как в системах ограниченной полосы можно применять методы эффективной (с точки зрения используемого спектра) модуляции для экономии полосы частот за счет увеличения расхода энергии.

