3.1. Системы координат и их представления. Метод координат
3.1.1. Системы координат и их представления
3.2. Уравнение прямой линии на плоскости
3.3. Уравнение плоскости в пространстве. Уравнения прямой в пространстве
3.3.1. Плоскость в пространстве
3.3.2. Нормальное уравнение плоскости
3.3.3. Условие параллельности двух плоскостей
3.4. Основные задачи на прямые и плоскости
3.4.1. Как найти точку пересечения двух прямых?
3.4.2. Как найти расстояние от точки до прямой?
3.4.3. Как разделить угол пополам?
3.4.4. Когда прямая пересекает отрезок?
3.4.5. Как найти отражённый луч?
3.4.6. Когда три прямые пересекаются в одной точке?
3.4.7. Когда три точки лежат на одной прямой?
3.4.8. Как найти треугольник по двум вершинам и центру?
3.4.9. Как найти треугольник по двум сторонам и центру тяжести?
3.4.10. Когда три плоскости пересекаются в одной точке?
3.4.11. Как найти расстояние от точки до плоскости?
3.4.12. Когда плоскость пересекает отрезок?
3.4.13. Как опустить перпендикуляр на плоскость?
3.4.14. Как найти угол между прямой и плоскостью?
3.4.15. Как найти точку пересечения прямой и плоскости?
3.4.16. Как найти плоскость, содержащую прямую и точку?
3.4.17. Как найти плоскость, содержащую прямую и параллельную другой прямой?
3.4.18. Как опустить перпендикуляр на прямую в пространстве?
3.4.19. Как найти расстояние от точки до прямой в пространстве?
3.1. Системы координат и их представления. Метод координат
3.1.1. Системы координат и их представления
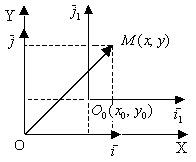
параллельный перенос
=
=
; 
; 
;
; 
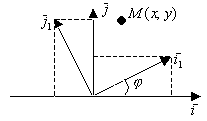
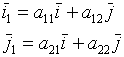
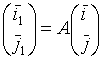
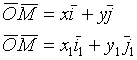
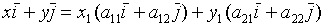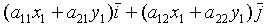
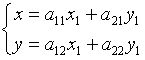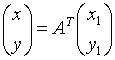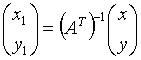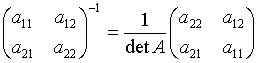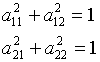
A - ортогональная, т.е.
; 
; 
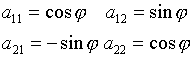
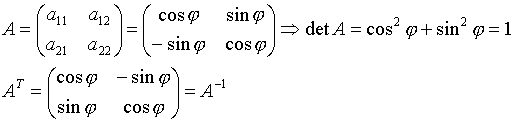
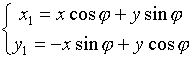(Ф-лы поворота)
Общий случай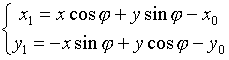 
3.1.2. Метод координат
наз-ся ур-нием линии, если каждая точка линии удовлетворяет этому ур-нию.
Алгебраической кривой наз-ся линия имеющая уравнение 
- многочлен от (x,y).
- порядок кривой (линии).
3.1.3. Теорема об инвариантности порядка
Если в некоторой ДСК кривая задается ур-нием порядка n, то в любой другой системе координат эта линия задается ур-нием такого же вида, такого же порядка.
Инвариантно - т.е. независимо от выбора системы координат.
(расстояние)
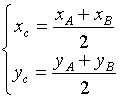середина отрезка (координат)
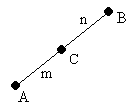
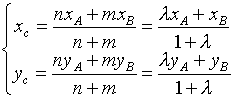формулы деления отрезка в данном отношении.
3.1.4. Полярная система координат
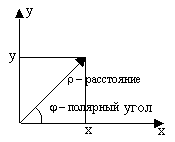
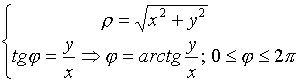
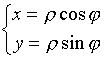
3.2. Уравнение прямой линии на плоскости
Теорема: Всякое линейное уравнение вида 
(общее уравнение прямой) определяет прямую на плоскости.
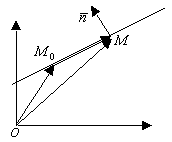
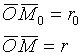Векторное уравнение прямой.
;
;
;
;
- векторное уравнение прямой
- уравнение прямой проходящей через данную точку с данным нормальным вектором 
- уравнение прямой проходящей через данную точку с заданным вектором(каноническое уравнение)
;
,
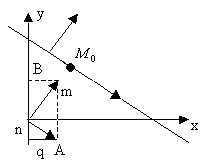
т.к.
или 
,где 
- уравнение прямой проходящей через заданную точку с данным угловым коэффициентом.
- уравнение прямой с данным угловым коэффициентом.
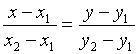- уравнение прямой проходящей через 2 заданные точки.
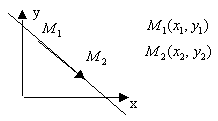
- уравнение прямой в отрезках
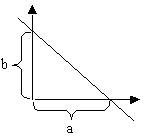
- нормальное уравнение прямой
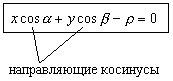
- расстояние от начала координат до прямой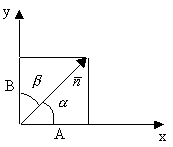 
;
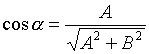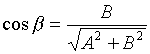
3.2.1. Параметрическое уравнение прямой
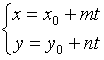
Условие параллельности двух прямых
;
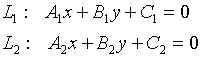
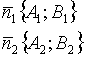
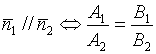Условие перпендикулярности двух прямых
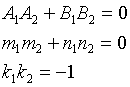
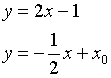
Угол между двумя прямыми 
.
=
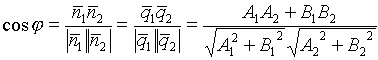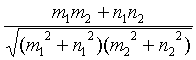
3.3. Уравнение плоскости в пространстве. Уравнения прямой в пространстве
3.3.1. Плоскость в пространстве
Определение: Любое линейное уравнение от 3-х переменных определяет плоскость в пространстве и обратно. 
- общее уравнение плоскости в пространстве 
- плоскость проходит через начало координат 
уравнение плоскости, проходящей через данную точку и данный нормальный вектор
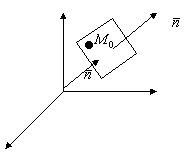
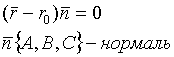
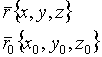
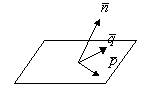
- направляющие вектора плоскости
- смешанное произведение 3-х векторов
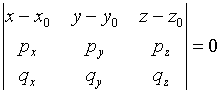- уравнение плоскости, проходящей через данную точку с данными направляющими векторами.
Пусть 
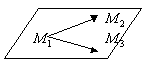
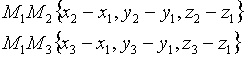
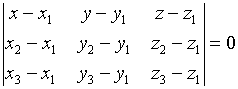x, y, z - текущие координаты
- уравнение плоскости в отрезках.
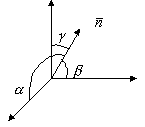
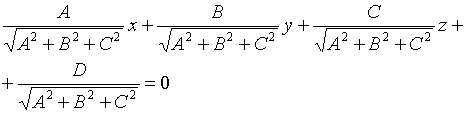
3.3.2. Нормальное уравнение плоскости
- нормальное уравнение плоскости
p - расстояние от начала координат до плоскости.
3.3.3. Условие параллельности двух плоскостей
;
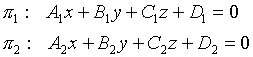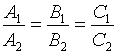
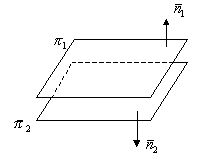
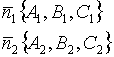
3.3.4. Условие перпендикулярности двух плоскостей
;
;
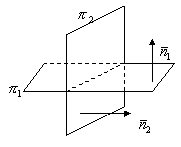3.3.5. Угол между плоскостями
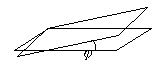
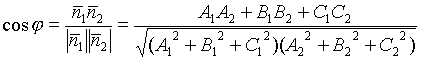
3.3.6. Прямая в пространстве
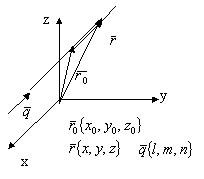
- векторное уравнение прямой в пространстве
t=
каноническое уравнение прямой
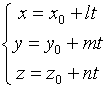- параметрическое уравнение прямой в пространстве
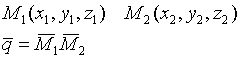
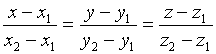- уравнение прямой, проходящей через 2 данные точки
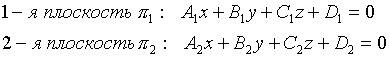
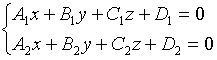- общее уравнение прямой в пространстве
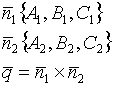
Пример.
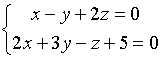
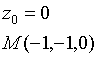
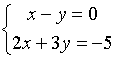
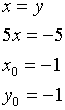
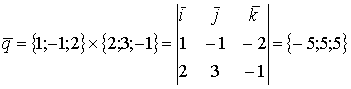
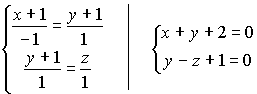
3.3.7. Условие параллельности 2-х прямых
; 
; 
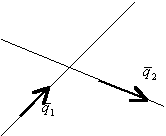
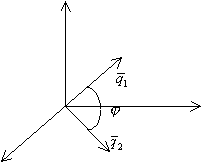
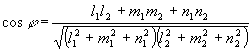
Если 
, то прямые перпендикулярны ортогонально.
3.4. Основные задачи на прямые и плоскости
3.4.1. Как найти точку пересечения двух прямых?
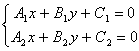
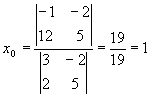
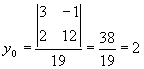
Точка пересечения (1;2).
3.4.2. Как найти расстояние от точки до прямой?
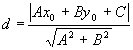
3.4.3. Как разделить угол пополам?
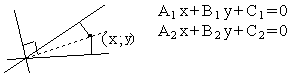
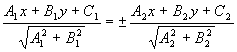
1) 
первая биссектриса "+"
2) 
вторая биссектриса
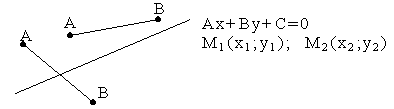
3.4.4. Когда прямая пересекает отрезок?
прямая пересекает отрезок.
Пример: 5x-y+1=0 M1(1;-1) ; M2(-3;2)
3.4.5. Как найти отражённый луч?
;
;
;
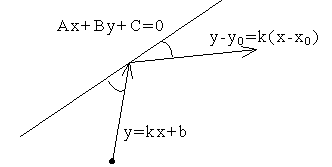
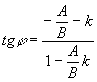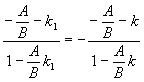
Пример:
y=2x+1 x-3y-2=0
x-3(2x+1)+2=0
-5x-1=0 
;
;
;
;
;
;
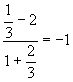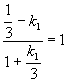3.4.6. Когда три прямые пересекаются в одной точке?
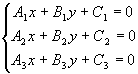имеет нетривиальное решение
;
;
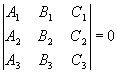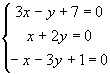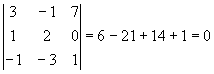
3.4.7. Когда три точки лежат на одной прямой?
A1(x1;y1) A2(x2;y2) A3(x3;y3)
;
;
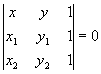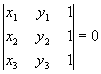
3.4.8. Как найти треугольник по двум вершинам и центру?
Дано: A, B, O - ортоцентр
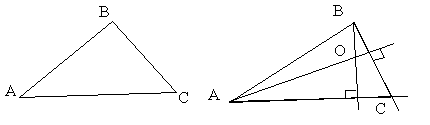
Пример: Дано: A(-5;5) B(3;1) O - ортоцентр (2;5)
;
;
x=3 4y=28
y=7 C(3;7)
3.4.9. Как найти треугольник по двум сторонам и центру тяжести?
(центру пересечения медиан)?
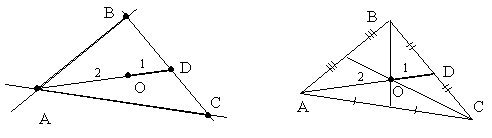
AB: 4x-5y+9=0 AC: x+4y-3=0
O(3;1) A(?;?)
По Крамеру: 
;
A(-1;1)
D - середина BC D(5;1)
BC: y-1=k(x-5) 
;
;
;
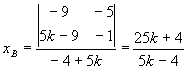
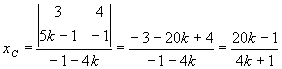
(25k+4)(4k+1)+(20k-1)(5k-4)-10(4k+1)(5k-4)
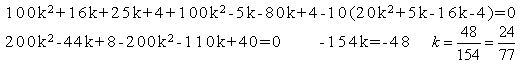
Некоторые способы решения задач
3.4.10. Когда три плоскости пересекаются в одной точке?
;
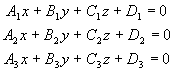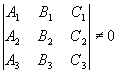
3.4.11. Как найти расстояние от точки до плоскости?
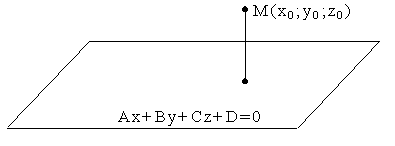
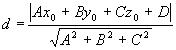
3.4.12. Когда плоскость пересекает отрезок?
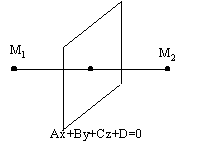
(Ax1+By1+Cz1+D)(Ax2+By2+Cz2+D)>0 M1 и M2 - по одну сторону
3.4.13. Как опустить перпендикуляр на плоскость?
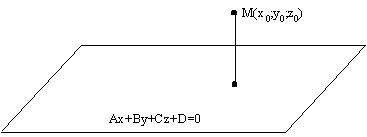
3.4.14. Как найти угол между прямой и плоскостью?
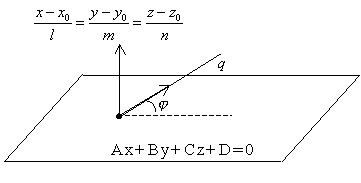
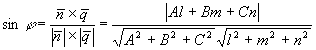угол всегда острый
3.4.15. Как найти точку пересечения прямой и плоскости?
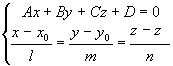2x-3y+z-5=0
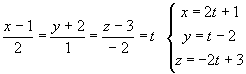2(2t+1)-3(t-2)+(-2t+3)-5=0
; 4t+2-3t+6-2t+3-5=0 ; -t+6=0 ; t=6
координаты точки пересечения
3.4.16. Как найти плоскость, содержащую прямую и точку?
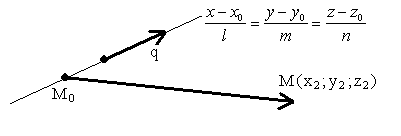
A(x-x0)+B(y-y0)+C(z-z0)=0
Пример: 
M(1;0;2) 
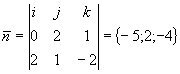; -5(x-1)+2(y-0)-4(z-2)=0
; -5x+5+2y-4z+8=0 -5x+2y-4z+13=0
3.4.17. Как найти плоскость, содержащую прямую и параллельную другой прямой?
; 
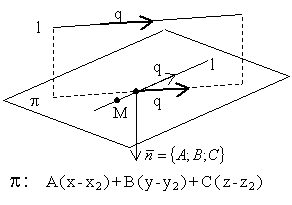
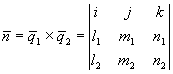
Пример: A(x-3)+B(y+4)+C(z-2)=0
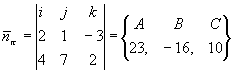
23(x-3)-16(y+4)+10(z-2)=0 ; 23x-69-16y-64+10z-20=0 ; 23x-16y+10z-153=0
3.4.18. Как опустить перпендикуляр на прямую в пространстве?
; 
Пример:
;
Решение: 
; 
; 
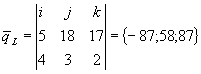3.4.19. Как найти расстояние от точки до прямой в пространстве?
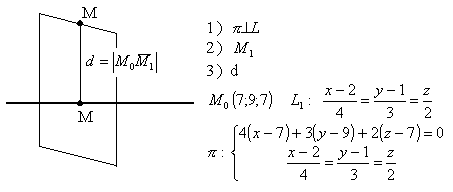
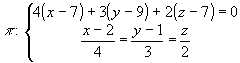
16t-20+9t-24+4t-14 ; 29t=58 t=2
3.4.20. Как найти расстояние между скрещивающимися прямыми?
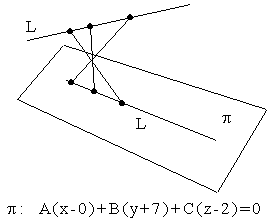Пример: 
; 
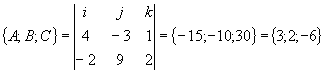; 3x+2(y+7)-6(z-2)=0
; 
3.4.21. Когда две прямые пересекаются?
; 
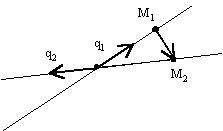
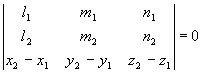
Пример: 
; 
; 
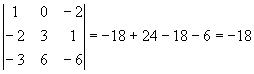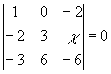
