4.1. Вводные замечания

4.2. Представления сообщений с помощью полиномов Лежандра

4.3. Представление сообщений с помощью функций Уолша

4.1. Вводные замечания

При дискретно – аналоговых представлениях с помощью регулярных выборок для получения малой ошибки интерполяции необходимо выбирать большую частоту опроса. При этом между соседними выборками появляются сильные корреляционные связи, что уменьшает пропускную способность канала передачи информации.

Для сокращения избыточности используют два пути:

1. Отказаться от использования в качестве координат регулярных выборок. При этом увеличивается эффективность представления путем изменения частоты опроса сигнала.

2. Использовать обобщенные дискретные представления, позволяющие сократить количество координат при условии, что корреляционные связи между отдельными отсчетами сигнала на интервале представления .

При обобщенных дискретных представлениях в результате анализа поведения функции на интервале представления формируется сообщение:

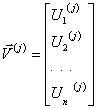, (4.1)

где - координаты, формируемые в результате анализа сигнала на интервале представления . Для этого весь интервал наблюдения разбивается на интервалы представления … и т.д.(рисунок 4.1)

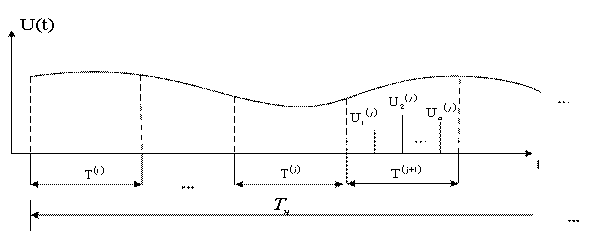
Рисунок 4.1

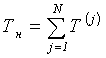. (4.2)

В результате анализа функции на интервале после окончания этого интервала формируется сообщение , которое передается в интервале представления. Обычно интервал представления выбирается равным:

, (4.3)

где - максимальный интервал корреляции, при .

Координаты получаются как коэффициенты разложения сигнала в функциональный ряд по базисным функциям

. (4.4)

На приемной стороне по переданным координатам восстанавливается первичный сигнал

, (4.5)

а координаты на передающей стороне определяют как коэффициенты функционального ряда:

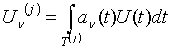, (4.6)

где - весовая функция, определенным образом связанная с .

Как следует из этого соотношения координата может быть представлена как результат фильтрации сигнала фильтра с импульсной характеристикой:

. (4.7)

Выбор лучшего обобщенного представления сводится к решению двух задач:

1. Выбор оптимального базиса . 2. Определение числа координат , обеспечивающих заданную точность восстановления функции.

Оптимальные базисы, минимизирующие число координат при заданной точности восстановления, связаны с вероятностными характеристиками первичного сигнала. Они описываются громоздкими выражениями и на практике неудобны. Обычно используют универсальные базисы , применение которых не требует сложных устройств обработки и , в тоже время , достаточно эффективно. Такие базисы выбирают в классе ортогональных функций:

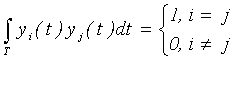. (4.8)

В качестве примера рассмотрим базисные функции в виде полиномов Лежандра и функций Уолша.

4.2. Представления сообщений с помощью полиномов Лежандра

Поместим начало отсчета времени в середину интервала представления:

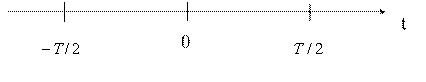
Рисунок 4.2

Введем нормированное время .При таких обозначениях полиномы Лежандра задаются соотношением:

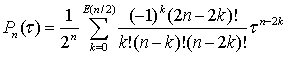, (4.9)

где - целая часть n/2. В частных случаях полиномы Лежандра имеют вид:

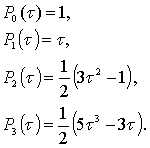(4.10)

Полиномы Лежандра при описываются рекуррентным соотношением:

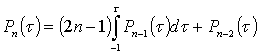. (4.11)

Графики первых четырех полиномов Лежандра приведены на рисунке 4.3:

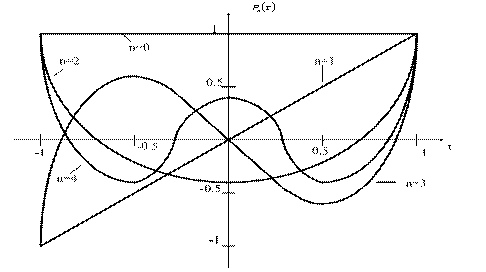
Рисунок 4.3

Структурная схема формирования полинома Лежандра имеет вид (рисунок 4.4):

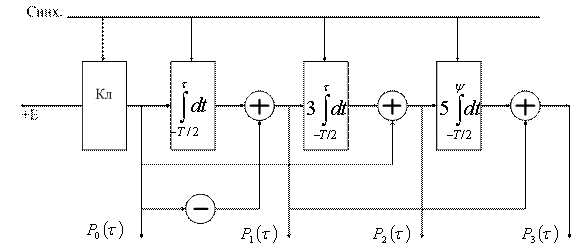
Рисунок 4.4

Структурная схема формирования координат изображена на рисунке 4.5, где

, (4.12)

- коэффициенты пропорциональности.

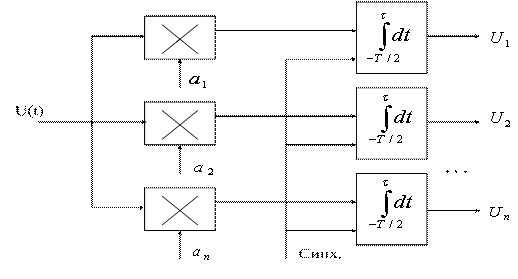
Рисунок 4.5

Недостатки обобщенных представлений с помощью полиномов Лежандра:

1. Сложность формирования весовых функций .
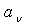2. Необходимость контроля коэффициента усиления каналов формирования координат .
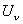3. Высокие требования к синхронизации.

При цифровом представлении весовых функций эти недостатки снимаются.

4.3. Представление сообщений с помощью функций Уолша

Использование этих представлений позволяет избежать многих недостатков представления сообщений с помощью полиномов Лежандра. Достоинством является простота реализации таких представлений с помощью цифровой техники.

Выберем начало отсчета времени у левой границы интервала представления (рисунок 4.6).

Рисунок 4.6

Введем нормированное время: , . При использовании функций Уолша число отсчетов следует выбирать так, чтобы выполнялось равенство: , где -целое число.

Функции Уолша строятся на основе базовых функций следующего вида (рисунок 4.7):

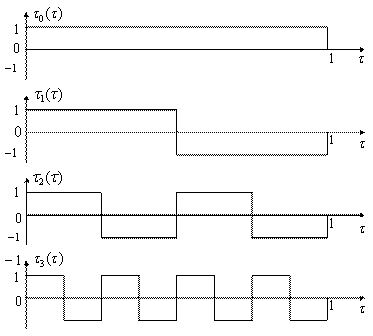
Рисунок 4.7

Базовые функции ортогональны, т.е. для них выполняется следующее условие:

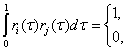
. (4.13)

Все функции Уолша находятся из соотношения:

, (4.14)

где , , - целые числа, .

Используя формулу (4.14), определим первые восемь функций Уолша: 1. ; 2. , , ; 3. , , ; 4. , , , ; 5. , , ; 6. , , , ; 7. , , , ; 8. , , , , ; Построим графики функций Уолша (рисунок 4.8). Функции Уолша также ортогональны:

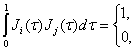
. (4.15)

Формирование функций Уолша возможно с помощью элементов цифровой техники. Структурная схема формирования функций Уолша имеет вид, представленный на рисунке 4.9.

Формирование координат производится в соответствии с выражением

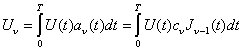. (4.16)

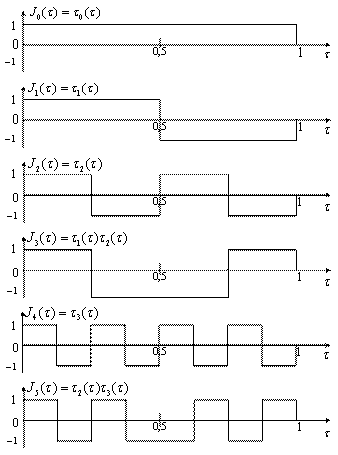
Рисунок 4.8

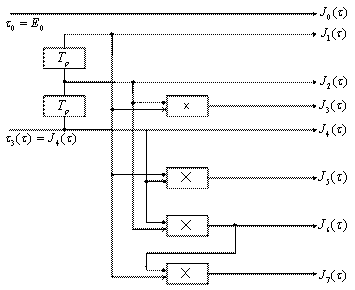
Рисунок 4.9

Недостатки обобщенных представлений с помощью функций Уолша:

1. Требуется большее число координат, чем при представлении с помощью полиномов Лежандра при той же точности.

2. Требуется большая полоса устройств формирования при реализации функций Уолша, чем при полиномах Лежандра.