3.1. Распространение плоских волн в диэлектрике и проводнике

3.2. Типы и классы электромагнитных волн

3.3. Особенности электромагнитных процессов в направляющих системах

3.4. Способы расчета направляющих систем

3.1. Распространение плоских волн в диэлектрике и проводнике

В один и тот же фиксированный момент времени значения фазы для плоской волны в точках пространства, расположенных на разных расстояниях и (например начало и конец направляющей системы) от излучателя, различны. Однако можно выбрать такое время для точки с расстоянием и время для точки с расстоянием , что фазы будут одинаковыми, т.е.

. Значит . Переходя к бесконечно малым приращениям и , получим общую формулу для определения этой скорости:

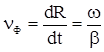. (3.1)

Скорость перемещения фазы поля называют фазовой скоростью.

На практике основной интерес представляет знание характеристик поля на очень больших расстояниях от излучателя, таких, что . В качестве такой характеристики используют отношение

, (3.2)

имеющее размерность Ом и зависящее от параметров среды, называемое характеристическим сопротивлением среды. В общем случае характеристическое сопротивление величина комплексная: т.е. . В частности, для плоской волны .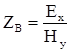

Принято считать среду диэлектриком если и проводником при .

Исходя из этого для диэлектрика имеем:

, т.е. ; (3.3)

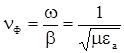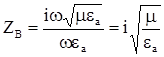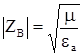; , . (3.4)

Для вакуума:

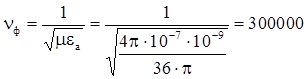км/c, т.е , где с скорость света.

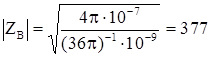Ом.

Для проводника имеем:

. Заменяя i на получим т.е. 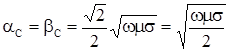. (3.5)

В таком случае

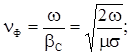
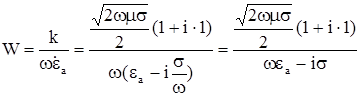;(3.6)

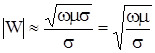. (3.7)

Электромагнитная плоская волна, попадая в метал, быстро затухает. Из уравнения распространения волны (2.13) следует, что процесс затухания определяется выражением . Если задаться уменьшением напряжения в раз на глубине , то эта глубина может быть определена из условия: . Откуда при 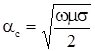имеем 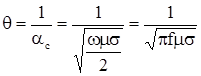. (3.8)

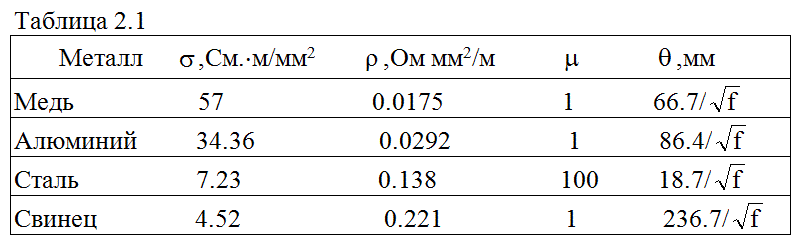
Величину принято называть эквивалентной глубиной проникновения поля. Расчетные соотношения глубины проникновения поля для некоторых металлов приведены в таблице:

Заметим что для идеального диэлектрика и потому диэлектрик является идеальной средой для распространения поля.

3.2. Типы и классы электромагнитных волн

Характер распространения ЭМ волн в направляющих системах (НС): структура поля и диапазонные свойства систем зависят от класса волны: используемой для канализации энергии.

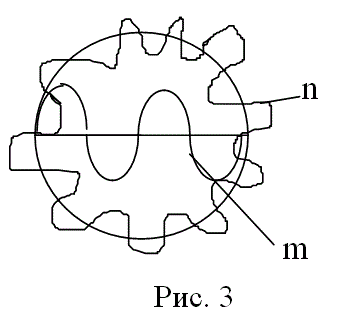
Существуют следующие классы волн (рис. 3):

T ¾ поперечно-электромагнитная (ТЕМ) (ТЕН);

Е ¾ электрическая или поперечно-магнитная ТН-волна;

Н ¾ магнитная или поперечно-электрическая ТЕ-волна;

ЕН и НЕ ¾ гибридные, смешанные волны.

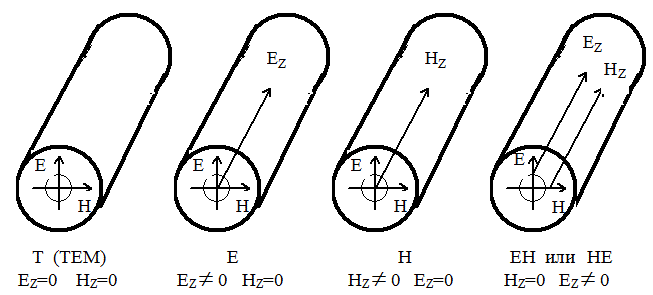
Рис. 1. Классы и типы волн

Волна Т ¾ основная волна, содержит только поперечные составляющие (электрического Е и магнитного Н полей), продольные составляющие Е_я и Н_я равны нулю, т.е. силовые линии поля целиком лежат в поперечных плоскостях и в точности повторяют картину силовых линий поля при статическом напряжении и постоянном поле. Волна Т существует лишь в линиях, содержащих не менее двух изолированных проводников, находящимися под разными потенциалами. Этот тип волны используется при передаче энергии в сравнительно ограниченном диапазоне частот по проводящим системам, где определяющими являются токи проводимости I_пр (Например, при передаче по симметричным, коаксиальным цепям и полосковым линиям). Процесс передачи Т-волн связан с потенциальным полем.

Волны Е и Н. Волны высшего порядка. Они содержат, кроме ЭМ полей (Е_^ и Н_^), по одной продольной составляющей поля. Для волн Е поле Е_z0, для волн Н поле Н_z0. Поэтому их силовые линии располагаются как в поперечных, так и в продольных сечениях направляющих систем. Эти волны возбуждаются в весьма высоком диапазоне частот. Здесь определяющими являются токи смещения I_см. Процесс передачи волн высшего порядка Е и Н связан с вихревым полем.

Волны Е и Н можно передавать по однопроводным НС, например, волноводам. Для этих волн необходима продольная составляющая поля Е или Н, которая задает направление движению энергии вдоль линии. Разность потенциалов создается между полюсами и стенками волновода. Поэтому по волноводу передаются очень короткие волны. Длина волн д.б. такой, чтобы в сечении волновода уложилось целое число полуволн (Рис. 4) или хотя бы одна полуволна.

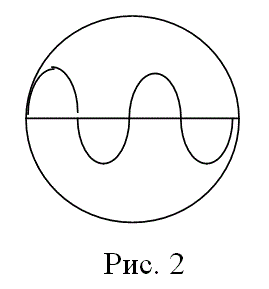
Гибридные или смешанные волны (ЕН, НЕ) представляют собой нераздельную сумму волн Е и Н и содержит все шесть компонентов поля, в том числе обе продольные составляющие Е_z и Н_z. К числу смешанных волн относятся волны, передаваемые по световодам и диэлектрическим волноводам.

Смешанные волны разделяются на:

НЕ ¾ с преобладанием в поперечном сечении поля Н;

ЕН ¾ с преобладанием в поперечном сечении поля Е.

Наряду с делением на классы ЭМ волны делятся также по типам. Тип волны, или мода, определяется сложностью структуры, т.е. числом максимумов м минимумов поля в поперечном сечении. Мода обозначается двумя числовыми индексами n и m.

Индекс n означает, например, в круглых волноводах число полных изменений поля по окружности волновода, а индекс m ¾ число изменений поля по диаметру.

3.3. Особенности электромагнитных процессов в направляющих системах

Потери энергии (затухание ) в направляющих системах. На потери энергии волн в направляющих системах оказывают влияние проводники и диэлектрики, встречающиеся на их пути. Это уменьшение передаваемой энергии оценивается затуханием сигнала через коэффициент

, (3.10) где

- коэффициент учитывающий потери части энергии, расходуемой на нагрев проводов при проникновении ЭМ поля внутрь проводника (за счет искажения линий электрического поля полем соседних проводников), а также потери вблизи лежащих проводниках в которых ЭМ поле вызывает вихревые токи;

- коэффициент, учитывающий диэлектрические потери (если диэлектрик не идеальный, например, как воздух);

- коэффициент учитывающий потери на излучение в свободное пространство.

Поверхностный эффект. В соответствии с выражением, полученным в предыдущей лекции, с ростом частоты переменного тока растет плотность тока у поверхности проводника. Неполное использование сечения проводника приводит к увеличению его сопротивления. Это и есть поверхностный эффект.

Эффект близости. Если проводники находятся достаточно близко, то в результате взаимодействия зарядов и токов этих проводников распределение полей меняется. В двухпроводных цепях переменное магнитное поле проводников вызывает перераспределение плотностей токов в этих проводниках по сечению. В симметричных и коаксиальных цепях эффект близости проявляется также как и поверхностный эффект, вызывая сосредоточение токов на поверхности проводников.

Сверхпроводимость. Ряд металлов (алюминий, цинк, титан, кадмий, ниобий, свинец, висмут и т.д.), а также многие сплавы при температурах близких к нулевым (2-10 К), переходят в сверхпроводящее состояние. Резко падает их сопротивления (более чем в 10¹¹ раз), поверхностный эффект достигает предела: электромагнитное поле не проникает в глубь проводника, ток практически течет по его поверхности и проводник приближается к идеальному. В нем отсутствуют потери.

Эффект сверхпроводимости используют для конструирования кабелей с чрезвычайно малыми потерями в металле и диэлектриках. Сейчас созданы синтетические материалы, проводники и диэлектрики, которые проявляют сверхпроводимость или резкое снижение диэлектрических свойств при температурах лишь на несколько десятков градусов ниже нуля по шкале Цельсия.

Электромагнитное экранирование. В технике передачи электрических сигналов очень важно избежать взаимных влияний между соседними цепями, а также влияние внешних электромагнитных полей, создающих помехи и опасные напряжения. Действенной мерой защитой от влияния переменных электромагнитных полей является электромагнитное экранирование. Оно основано на том, что проникая из диэлектрика в металл, сильно затухает, распространяясь в металле. Экранирующее действие тем сильнее, чем толще экран, чем больше магнитная проницаемость и меньше удельное сопротивление металла, а также частота изменения поля. С удалением экрана от экранируемых цепей эффект экранирования возрастает. Одновременно уменьшаются потери в экране на вихревые токи, т.е. снижается затухание в цепи. Однако увеличение диаметров экранов в кабелях экономически невыгодны, так как приводит к увеличению поперечного сечения кабеля и дополнительному расходу материала.

3.4. Способы расчета направляющих систем

В зависимости от диапазона используемых частот, конструкции направляющей системы, вдоль которой распространяется электромагнитная энергия, можно условно выделить два различных способа расчета: с использованием уравнений поля и уравнений теории цепей.

Хотя способ основанный на использовании уравнений поля является универсальным из-за сложности в явном виде его используют для расчета электромагнитных процессов в области достаточно высоких частот, когда в первом уравнении системы ( ) необходимо учитывать слагаемое , характеризующее изменение магнитного поля тока смещения в пространстве. Например, при расчете металлических волноводов (учитывают токи смещения и проводимости) и диэлектрических волноводов (учитывают только токи смещения).

Инженерный расчет с применением уравнений теории цепей более простой по сравнению с прямым решением уравнений Максвелла. Электромагнитное поле в уравнениях линии не фигурирует явно. В место него для каждого поперечного сечения линии передачи в каждый момент времени определяют две величины - напряжение и ток . При этом каждый однородный участок цепи характеризуется четырьмя параметрами: активным сопротивлением , индуктивностью , ёмкостью , и проводимостью изоляции , численные значения которых зависят от конфигурации электромагнитного поля, связанного с данной направляющей цепью.

Уравнения теории цепей используют также при расчетах взаимных влияний между цепями и при расчетах воздействий внешних магнитных полей от высоковольтных линий электропередачи на цепи телемеханики и связи.

Однако прежде чем пользоваться методами расчета теории цепей необходимо получить значения параметров входящих в эти уравнения. Для этого также эффективно используют уравнения поля.