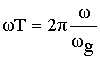1. Дискретизация непрерывных сигналов
2. Связь спектров дискретных и непрерывных сигналов
3. Преобразования Фурье и Лапласа для дискретных сигналов
5. Основные свойства Z-преобразования
8. Алгебраизация разностных уравнений
9. Передаточная функция дискретной цепи
10. Частотные характеристики дискретной цепи
11. Общие свойства передаточной функции дискретной цепи
13. Расчет сигнала на выходе цепи применением свертки
15. Энергия дискретного сигнала
16. Расчет энергии сигнала дискретной цепи
18. Расчет не рекурсивного ЦФ общего вида
20. Общие свойства фильтра с линейной фазой
21. Расчет фильтров с линейной фазой
23. Расчет рекурсивных фильтров
24. Эффекты конечной разрядности и их учет
25. Расчет усредненной энергии шума
26. Влияние структуры цепи на шум квантования
28. Масштабирование сигнала в цепи
29. Оценка эффективности использования динамического диапазона цепи
31. Чувствительность цифровых фильтров
32. Быстрое преобразование Фурье
33. Алгоритм инверсно кодированных перестановок
35. Параллельные соединения ЦФ
36. Оптимальная обработка сигнала
37. Перенос спектра сигнала в заданную область. Выделение боковой (нижней или верхней)
1. Дискретизация непрерывных сигналов
Цифровые системы связи вырабатывают дискретные сигналы, которые получаются из непрерывных путем дискретизации.
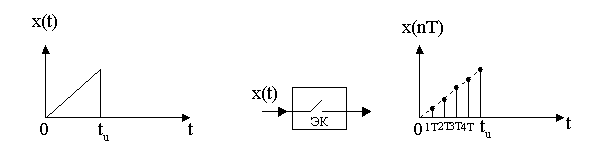
Схема дискретизации:
fg– частота дискретизации
Т – интервал дискретизации
X(t) – непрерывный (аналоговый) сигнал
X(nТ) – дискретный сигнал
X(nТ) = X(n) = Xn = {X0; X1; X2; … } – обозначения дискретного сигнала.
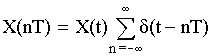– формула связи дискретного и аналогового сигналов.
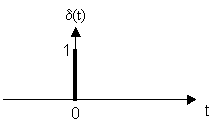
– дискретная 
– функция.
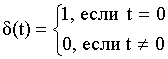
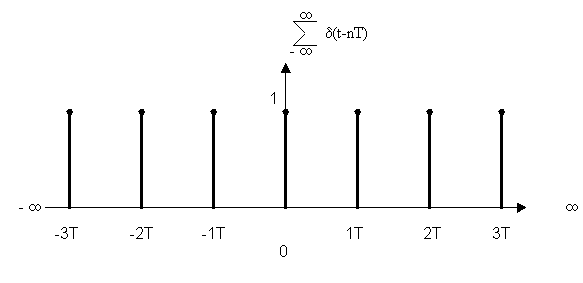
– периодическая последовательность 
– функции, следующая с интервалом T.
2. Связь спектров дискретных и непрерывных сигналов
Пусть 
– спектр дискретного сигнала x(nТ);
(jω) – спектр исходного аналогового сигнала x(t).
Для установления связи между спектрами воспользуемся прямым преобразованием Фурье:
Раскладываем в ряд Фурье:
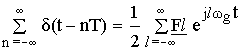
Fl– амплитуда гармоник.
Определим Fl используя формулу связи между спектрами периодических и непериодических сигналов.
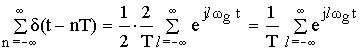
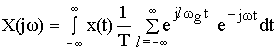
В силу линейности операции в этом выражении знаки 
и 
можно поменять местами.
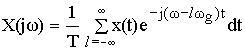
Воспользуемся теоремой смещения (теорема о спектрах).
Если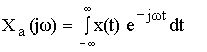 
, то:
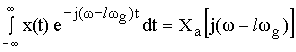
Формула связи спектров дискретного и аналогового сигналов имеет вид:
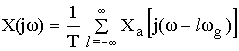
Вывод: спектр дискретного сигнала равен сумме равно-смещенных спектров аналогового сигнала, сдвинутых на величину кратных 
.
Полученный результат продемонстрируем на графиках.
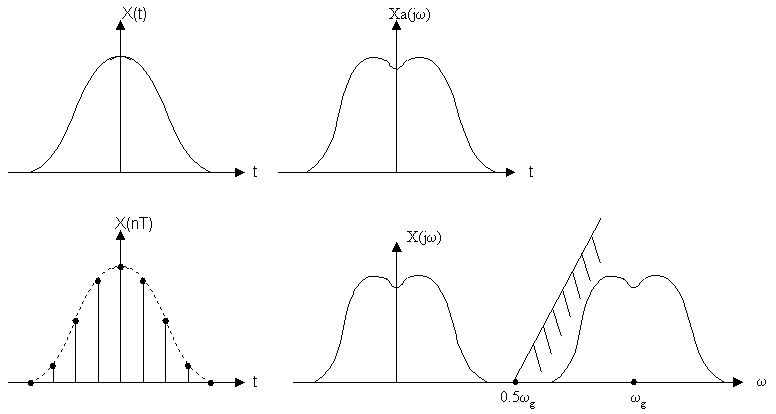
Если 
, то спектр дискретного и аналогового сигналов совпадает (X(jω) и Xa(jω) совпадают) на интервале [-0.5ωg;0.5ωg]. В результате x(t) аналоговый сигнал можно восстановить применением ФНЧ с частотой среза ωс=0.5ωg.
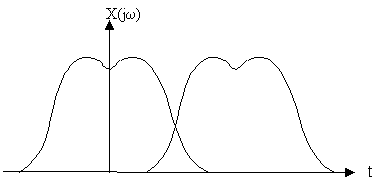
Если ωв>0.5ωg, то смежные спектры перекрываются и возникают ошибки наложения, погрешности (не устранимые), поэтому восстановить такой сигнал можно только с искажением (искажения могут оказаться значительными).
3. Преобразования Фурье и Лапласа для дискретных сигналов
Формула Фурье для дискретного сигнала:
– прямое преобразование Фурье.
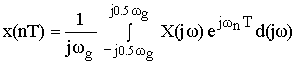– обратное преобразование Фурье.
Сигнал x(nT) нормирован по отношению к X. 
После денормирования сигнала формулу записываем в виде:
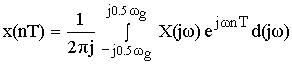
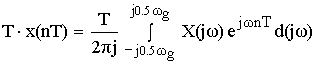
Устремляем T к нулю. Если 
, то T вырождается в непрерывную переменную 
Денормированные формулы прямого и обратного преобразования Фурье для непрерывных сигналов:
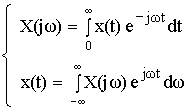
Это доказывает справедливость формулы Фурье для дискретного сигнала. Переменную ω можно распространить на всю плоскость комплексного переменного: 
, и тогда формулы Фурье для дискретного сигнала заменяются формулами Лапласа.
– прямое преобразование.
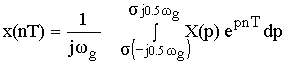– обратное преобразование.
4. Z – преобразования
Изображение по Лапласу дискретных сигналов X(p) является функцией трансцендентной, что значительно затрудняет частотный анализ дискретных сигналов. Переменную p, находящуюся в показателе экспоненты, заменяют:
X(p) заменяется на рациональную функцию, что упрощает частотный анализ.
X(Z) – Z-изображение дискретного сигнала x(nT).
Если в формулах Лапласа сделать замену:
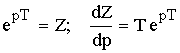
В результате получаем формулы Z-преобразования:
– прямое Z-преобразование.
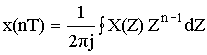– обратное Z-преобразование.
Рассмотрим особенности перехода от плоскости комплексного переменного p=σ+jω к плоскости комплексного переменного Z=x+jy.
, пусть σ=0, т.е. p=jω тогда:
где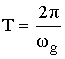 
Если ω=0, то Z=1.
Если ω=0.5ωg, то 
.
Если ω=ωg, то 
.
При увеличении переменной ω, переменная Z осуществляет многократное перемещение по единичной окружности.
По изображению X(Z) можно получить спектр дискретного сигнала, для этого вместо Z надо подставить:
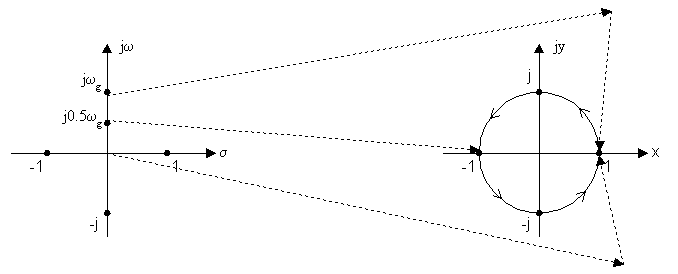
Точкам в левой полуплоскости комплексного переменного p соответствуют значения переменной внутри единичного круга на плоскости Z.
Пример 1:
Определить Z-изображение сигнала.
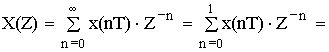
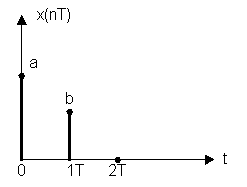
Пример 2:
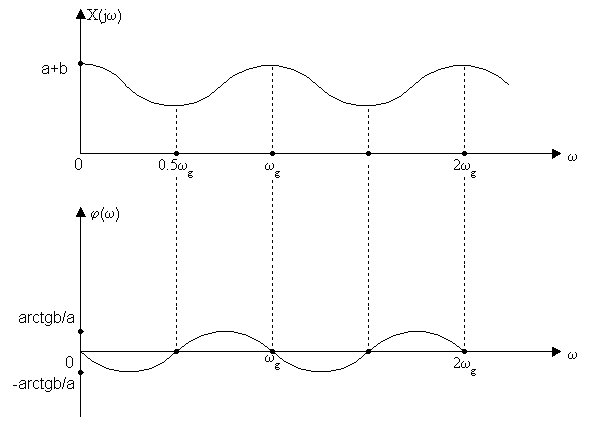
Определить спектр сигнала (пример 1).
|
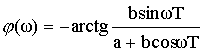
ω |
0 |
0.5ωg |
ωg |
|
|
0 |
π |
2π |
|
sinωT |
0 |
0 |
0 |
|
cosωT |
+1 |
-1 |
+1 |
|
|
a+b |
a-b |
a+b |
|
φ(ω) |
0 |
0 |
0 |
5. Основные свойства Z-преобразования
1. Линейность:
Если 
, то 
.
2. Запаздывание:
Если 
3. Свертка:
Если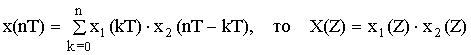 
4. Умножение:
Если 
, то
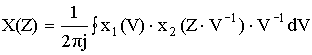
V, Z – переменные на плоскости Z.
5. Равенство Парсеваля (теорема энергии):
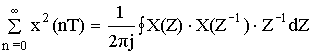
Дискретное преобразование Фурье (ДПФ).
Если сигнал x(nT) ограничен одновременно по времени некоторым значением tи, и по частоте fв, то он характеризуется конечным числом отсчетов N как во времени, так и в частотных областях.
Во временной области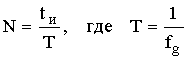 
;
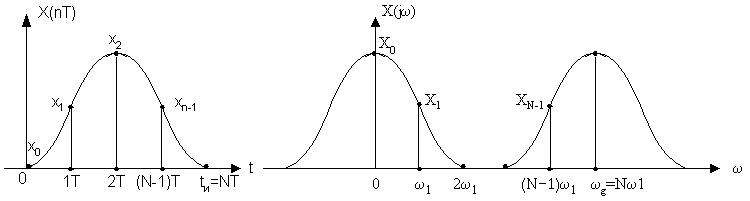
В частотной области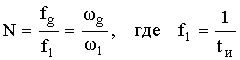 
– это интервал между смежными отсчетами спектра.
ωg – тактовая частота
Отсчеты сигнала x(nT) являются коэффициентами Фурье периодической последовательности X(jω) с периодом ωg. Это следует из формулы прямого преобразования Фурье для дискретных сигналов.
Отсчеты в частотной области (X0,X1,…) тоже являются коэффициентами Фурье периодической последовательности x(t) с периодом tи.
Отсчеты во временной и частотной области связаны между собой формулами ДПФ. Формулы ДПФ следуют из формул для дискретных сигналов.
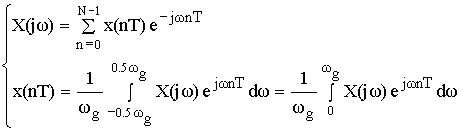
В этих формулах перейдем к дискретной переменной kω1 от непрерывной переменной ω.
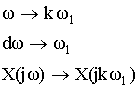
В результате такого перехода исходная пара преобразований принимает вид:
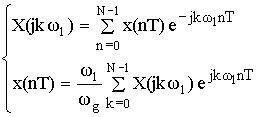
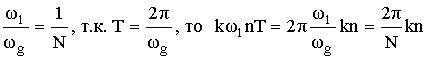
В результате формула принимает вид:
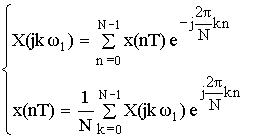прямое и обратное ДПФ
Пример:
, где a и b положительные вещественные числа a>b.
Определить отсчеты спектра
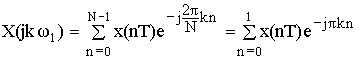
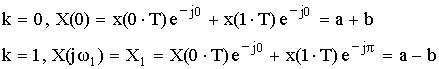
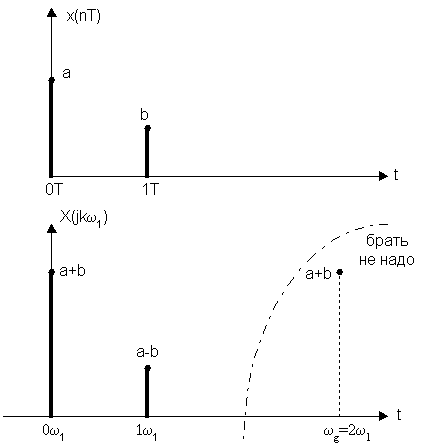
В качестве проверки по частотным отсчетам найдем временные.
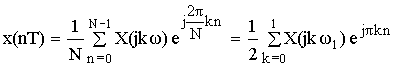
6. Дискретные цепи
Обычная аналоговая (RL-цепь) цепь описывается дифференциальными уравнениями. Если непрерывную переменную t заменить на дискретно изменяющуюся переменную nT, то дифференциальные уравнения вырождаются в разностные уравнения. Разностные уравнения общего вида, в котором в явной форме выражены прямые и обратные связи и который связывает сигналы на входе и выходе имеют следующий вид:
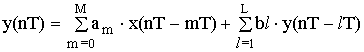– разностное уравнение общего вида,
где: x(nT) – сигнал на входе цепи,
y(nT) – сигнал на выходе,
M – число прямых отводов,
(L-1) – число обратных отводов,
m, l – целые числа,
am, bm – вещественные коэффициенты.
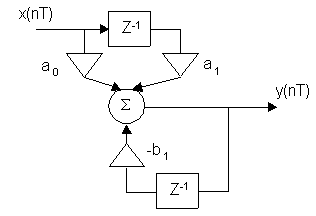
Такому уравнению соответствуют цепи, которые называют дискретной цепью.
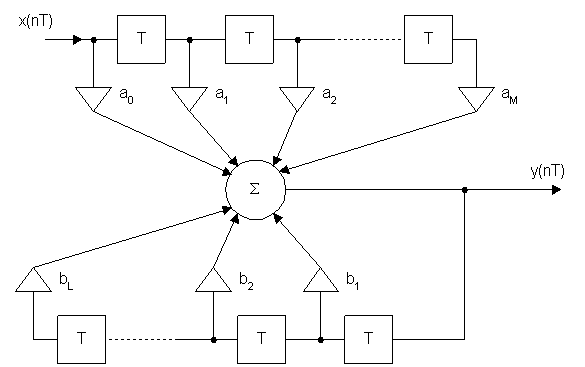
Элемент запаздывания на время T или элемент памяти.
Сумматор.
Т – интервал дискретизации поступающего сигнала,
ai,bi– умножители на коэффициент ai или bi.
Схема разностной цепи и значение коэффициентов ai и bi определяют способ обработки сигналов, поступающих на вход цепи. Расчет выходного сигнала y(nT) осуществляется путем решения разностного уравнения. Существуют аналитические и численные способы решения разностных уравнений.
Аналитические способы позволяют получить решение в общем виде, сделать анализ. Численные способы дают ответ в виде числовой последовательности.
7. Разностные уравнения
Разностные уравнения – это алгоритм функционирования дискретной цепи. Разностное уравнение записывается непосредственно по схеме.
Пример: Составить разностное уравнение.
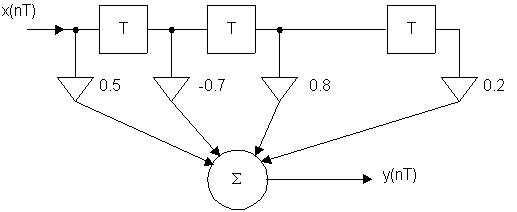
y(nT) = 0.5·x(nT) + (-0.7) ·x(nT-T) + 0.8·x(nT-2T) + 0.2·x(nT-3T)
Пример: Определить y(nT) если x(nT)={1;0.5} для цепи:
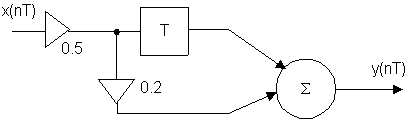
y(nT) = 0.1·x(nT) + 0.5·x(nT-T)
Воспользуемся численным методом.
n=0; y(0T) = 0.1·x(0T) + 0.5·x(-T) = 0.1 + 0.5·0 = 0.1
n=1; y(1T) = 0.1·x(1T) + 0.5·x(0T) = 0.1·0.5 + 0.5·1 = 0.55
n=2; y(2T) = 0.1·x(2T) + 0.5·x(1T) = 0.1·0 + 0.5·0.5 = 0.25
n=3; y(3T) = 0.1·x(3T) + 0.5·x(2T) = 0.1·0 + 0.5·0 = 0
y(nT) = {0.1; 0.55; 0.25}
Пример: Определить сигнал на выходе, если x(nT) = {1; 1}
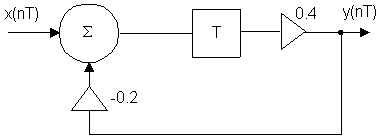
Цепь с обратной связью.
Составим разностное уравнение из двух слагаемых:
y(nT) = 0.4·x(nT-T) – 0.2·0.4·y(nT-T)
вх.сигнал вых.сигнал
n=0; y(0T) = 0.4·x(-T) – 0.08·y(-T) = 0, где: x(-T) = y(-T) = 0
n=1; y(1T) = 0.4·x(0T) – 0.08·y(0T) = 0.4·x(T-T) – 0.08·y(T-T) = 0.4·1-0.08·0 = = 0.4
n=2; y(2T) = 0.4·x(1T) – 0.08·y(1T) = 0.4·1 – 0.08·0.4 = 0.4 – 0.032 = 0.368
n=3; y(3T) = 0.4·x(2T) – 0.08·y(2T) = 0.4·0 – 0.08·0.368 = –0.02944
n=…
y(nT) = {0; 0.4; 0.368; –0.2944; …}
Цепь дискретная, содержащая обратную связь, называется рекурсивной, а цепь, не содержащая обратной связи, называется не рекурсивной.
8. Алгебраизация разностных уравнений
Разностные уравнения становятся алгебраическим уравнением, если сигналы заменить их Z-изображениями.
Рассмотрим это на примере общего вида:
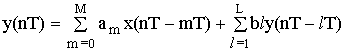
X(nT) Þ X(Z), y(nT) Þ Y(Z)
x(nT–mT) Þ X(Z)·Z-m,
y(nT–lT) Þ Y(Z)·Z-l
В результате теоремы линейности получим:
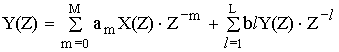алгебраическое уравнение относительно Z.
Алгебраическое уравнение существенно проще разностного уравнения.
В результате эффективность анализа расчета становится выше.
9. Передаточная функция дискретной цепи
Передаточная функция дискретной цепи определяется отношением:
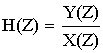
Получим выражение общего вида для передаточной функции дискретной цепи. Для этого используем алгебраическое уравнение общего вида:
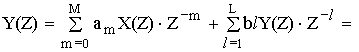
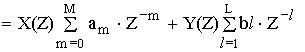
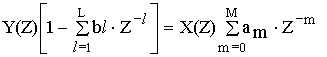
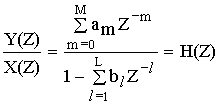передаточная функция рекурсивной цепи общего вида.
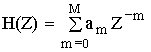передаточная функция не рекурсивной цепи общего вида.
Найдем передаточную функцию элемента запаздывания:
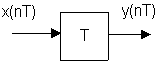
y(nT) = x(nT–T)
Y(Z) = X(Z)·Z-1 H(Z) = Z-1
Передаточная функция дискретной цепи определяется непосредственно по схеме, теми же методами, что и цепи RLC.
Для цепи с обратной связью используется формула:
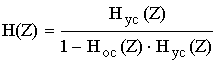
Hyc(Z)–передаточная функция участка цепи прямого прохождения сигнала.
Hoc(Z)–передаточная функция обратной связи .
Пример 1: Определить передаточную функцию цепи.
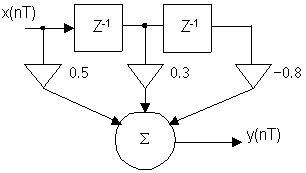
H(Z) = 0.5 + 0.3·Z-1– 0.8·Z-2
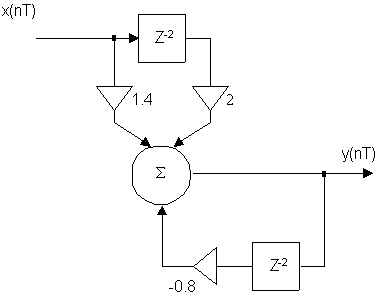
Пример 2: Определить передаточную функцию.
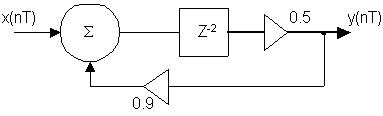
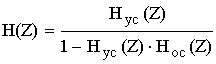
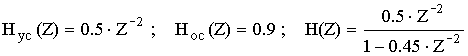
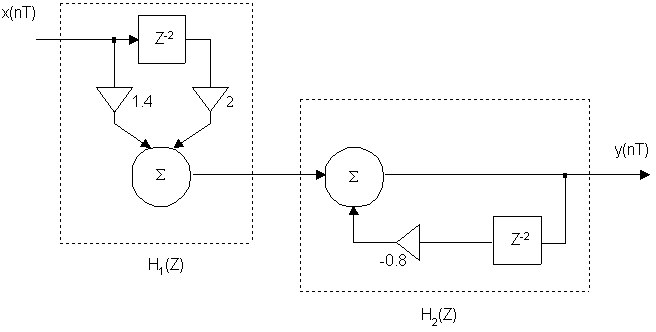
Пример 3: Определить передаточную функцию.
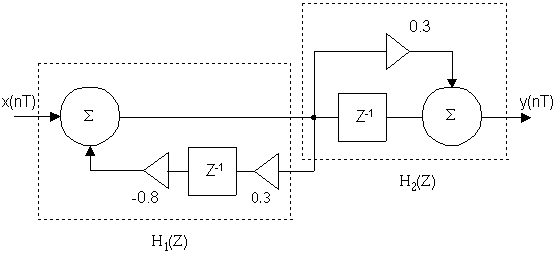
Первый участок цепи рекурсивный, есть обратная связь.
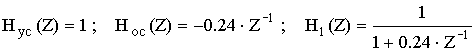
Второй участок цепи нерекурсивный.
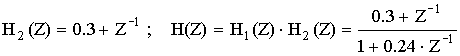
10. Частотные характеристики дискретной цепи
Частотные характеристики определяются по известному выражению H(Z) для H(Z) общего вида:
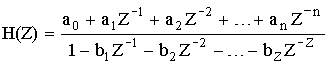
Частотные характеристики получаются после замены: 
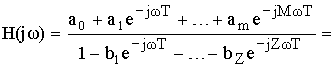
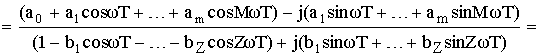
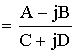
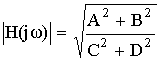– АЧХ.
– ФЧХ.
При расчетах и проектировании дискретных цепей вводят нормирование по частоте.
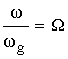; т.е. при ω=0 → Ω=0
при ω= ωg → Ω=1
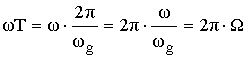
11. Общие свойства передаточной функции дискретной цепи
Для дискретной цепи общего вида передаточная функция является рациональной функцией и записывается так:
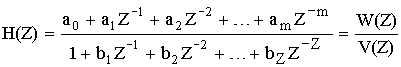
Согласно этому выражению можно сделать заключение общего характера: любая рациональная функция от Z может быть реализована в виде дискретной цепи. Передаточная функция, которая совпадает с заданной рациональной функцией с точностью до постоянного множества ZQ при условии, что заданная рациональная функция удовлетворяет следующим требованиям:
1. коэффициенты аi и bi–вещественные числа.
2. Корни уравнения V(Z)=0 расположены в пределах единичного круга на плоскости Z.
Второе замечание касается устойчивости цепи (цепь устойчива если полюсы H(p) расположены в левой полуплоскости комплексной переменной p, но, при переходе к плоскости Z, левая полуплоскость p отображается на единичный круг плоскости Z.
Пример: Задана рациональная функция (дробная):
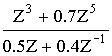Преобразим эту функцию по форме передаточной функции общего вида.
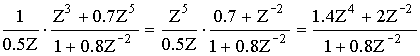
Z4= ZQ
1 + 0.8Z-2 = 0
Z2 + 0.8 = 0
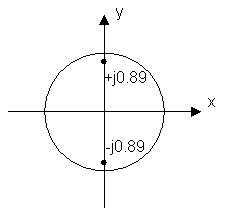
Цепь устойчивая.
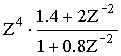
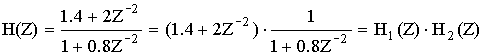
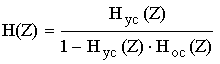
12. Импульсная характеристика
Импульсная характеристика и передаточная функция являются общими характеристиками цепи.
h(nT) – импульсная характеристика,
H(Z) – передаточная функция.
Обе характеристики связаны Z – преобразованиями.
При проектировании дискретной цепи требования к цепи задаются в виде требований импульсной характеристики цепи или передаточной функции.
Обычно схему цепи строят по известной передаточной функции. Если схема цепи известна, то импульсную характеристику можно получить одним из следующих способов:
1) непосредственно по схеме, как реакцию цепи на δ–функцию;
2) решением разностного уравнения, полагая: x(nT)= δ(nT), y(nT)=H(nT);
3) по известной передаточной функции H(Z):
a) применяя обратное Z–преобразование,
b) применяя теоремы разложения для H(Z) (аналогично определению оригинала по известному изображению),
c) делением числителя H(Z) на знаменатель с последующим применением теорем линейности и запаздывания (простой способ).
Пример простого способа: Определить h(nT), если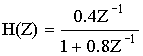 
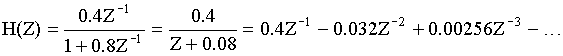
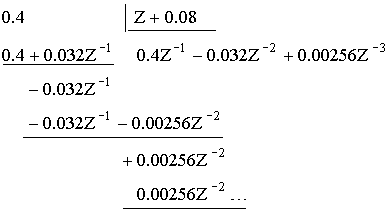
Применяя теорему линейности и запаздывания, получаем h(nT).
h(nT) = {0; 0.4; -0.032; 0.00256; …}
13. Расчет сигнала на выходе цепи применением свертки
Линейная свертка.
Спектр сигнала на выходе цепи равен произведению входного сигнала на передаточную функцию, т.е.
Y(jω) = X(jω) · H(jω)
В равной мере это относится и к Z–изображениям:
Y(Z) = X(Z) · H(Z)
Но произведению Z–изображений соответствует свертка сигнала:
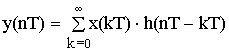– формула линейной свертки.
Пример: h(nT) = {1.0; 0.5}
Определить y(nT), если x(nT) = {0.8; 1.0}. Верхний предел можно взять n.
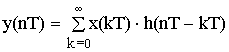
n=0; y(0T) = x(0T)·h(0T) = 0.8·1.0 = 0.8
n=1; y(1T) = x(0T) ·h(1T) + x(1T) ·h(0T) = 0.8·0.5 + 1.0·1.0 = 1.4
n=2; y(2T) = x(0T) ·h(2T) + x(1T) ·h(1T) + x(2T) ·h(0T) =
= 0.8·0 + 1·0.5 + 0·1 = 0.5
Ответ: y(nT) = {0.8; 1.4; 0.5}
Круговая свертка.
Спектр периодического сигнала является дискретным, поэтому спектр на выходе периодического сигнала определяется произведением дискретных спектров.
Y(jkω1) = X(jkω1) · H(jkω1)
Это выражение имеет смысл лишь в том случае, когда периоды всех сигналов (y(nT), x(nT), h(nT)) одинаковы и следовательно число частотных отсчетов будет одинаковым для всех сигналов.
Если периоды сигналов будут разными, то все периоды выравниваются по максимальному периоду, а недостающие отсчеты заменяются нулями.
NT– число отсчетов в периоде, где больше период сигнала.
Произведению дискретных спектров соответствует свертка периодических сигналов на интервале равным одному периоду.
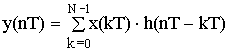– формула круговой свертки.
Сигнал на выходе цепи имеет наибольшее количество отсчетов по сравнению с x(nT) и h(nT), т.е.
если N1 – число отсчетов x(nT)
N2 – число отсчетов h(nT),
то N = N1 + N2 – 1 – число отсчетов y(nT).
Пример: Исходные данные из предыдущего примера.
x(nT) = {0.8; 1.0} h(nT) = {1.0; 0.5}
N1 = 2 ; N2 = 2 ; N = 2 +2 – 1 = 3
X(nT) = {0.8; 1.0; 0} h(nT) = {1.0; 0.5; 0}
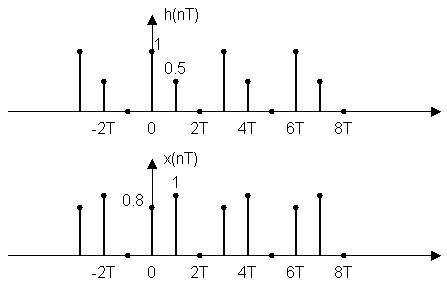
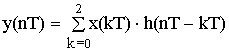
n = 0; y(0T) = x(0T)·h(0T) + x(1T) ·h(-1T) + x(2T) ·h(-2T) =
= 0.8·1 + 1·0 + 0·0.5 = 0.8
n = 1; y(1T) = x(0T)·h(1T) + x(1T) ·h(0T) + x(2T) ·h(-T) =
= 0.8·0.5 + 1·1 + 0·0 = 1.4
n = 2; y(2T) = x(0T)·h(2T) + x(1T) ·h(1T) + x(2T) ·h(0T) =
= 0.8·0 + 1·0.5 + 0·1 = 0.5
y(nT) = {0.8; 1.4; 0.5}
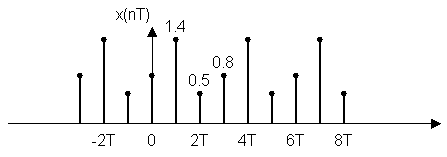
14. Секционирование
Реальные сигналы, поступающие на вход цепи для обработки, могут иметь большую протяженность, поэтому эти сигналы приходится секционировать, т.е. разбивать на секции.
xi(nT) – секция входного сигнала.
Секцию можно представить как дискретную периодическую последовательность и использовать круговую развертку.
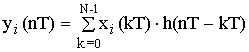– секция выходного сигнала.
– выходной сигнал.
На практике получили распределение два метода по секционной обработке.
1. Метод перекрытия с суммированием.
Входной сигнал разбивается на секции длиной L.
N1 = L – длина секции xi(nT)
N2 – длина h(nT)
N = N1 + N2 –1 – длина секции yi(nT)
Длина секции выходного сигнала больше длины секции входного сигнала на (N2 –1) отсчетов. Смежные секции выходного сигнала перекрываются на интервале (N2 –1). На этом интервале необходимо производить суммирование отсчетов.
2. Метод перекрытия с накоплением.
Входной сигнал разбивается на секции длиной L. Каждая секция наращивается слева (N2 –1) – отсчетами от предыдущей секции, в результате:
N1 = L +(N2 –1) – длина удлиненной секции xi(nT)
N2 – длина h(nT)
N = N1 + N2 –1 = L + 2(N2 –1) – длина секции yi(nT)
В результате искусственного удлинения входной секции, (N2 –1) отсчетов слева и (N2 –1) отсчетов справа выходной секции являются ложными и поэтому отбрасываются. Оставшиеся L отсчетов являются истинными и поступают на выход (они не перекрываются).
Дополнительной арифметической операции не требуется т.к. секции перекрываются.
Посекционная обработка применяется в том случае, когда дискретная система реализована в виде программы на ЭВМ. Если дискретная цепь состоит из реализованных отдельных элементов (умножителей, сумматоров, элементов памяти, т.е. в виде цепи), то необходимости посекционной обработки нет.
15. Энергия дискретного сигнала
В качестве энергии Wx дискретного сигнала x(nT) применяется мера:
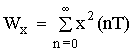
Энергию можно вычислить и в частотной области, применяя равенство Парсеваля:
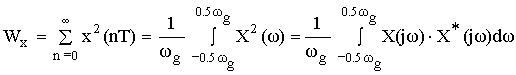
– спектр сигнала x(nT).
– спектр инверсного сигнала x(-nT).
X(jω) · X*(jω) = X2(ω) = Sx(jω) – энергетический спектр сигнала x(nT).
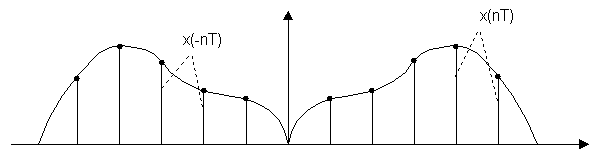
Энергетическому спектру Sx(jω) соответствует во временной области корреляционная функция Sx(nT) сигнала x(nT).
В соответствии с определением энергетического спектра корреляционная функция определяется сверткой сигнала с инверсной копией.
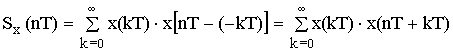– формула корреляции сигнала x(nT).
Согласно формуле корреляции в точке:
n = 0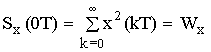 
Если Sx(jω) – спектр непрерывного сигнала Sx(nT), то Sx(jmω1) – спектр периодической дискретной последовательности Sx(nT).
Периодическая дискретная последовательность Sx(nT) определяется через свой спектр по формуле обратного ДПФ.
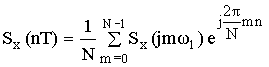
При n = 0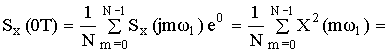 
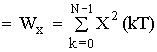– равенство Парсеваля для периодической дискретной последовательности.
16. Расчет энергии сигнала дискретной цепи
Расчет корреляционной функции на выходе цепи:
корреляционная функция выходного сигнала – Sy(nT), Sx(nT) и Sh(nT).
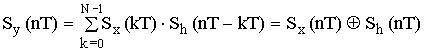
Где 
– условное обозначение свертки.
Докажем справедливость этой формулы:
т.к. система линейная и математические операции линейные, то сигнал можно сочетать различными способами 
Согласно полученному выражению энергию полученного сигнала можно получить без расчета выходного сигнала.
n = 0 
Рассмотрим важный частный случай: пусть x(nT) – случайный сигнал с нулевым средним. Для такого сигнала:
Sx(nT) = Sx(0T) = Wx = σx2 – дисперсия сигнала x(nT)
Тогда 
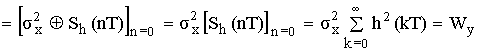
– формула расчета выходного сигнала (применяется для расчета шумов квантования в цифровых фильтрах).
Пример: определить энергию сигнала на выходе цепи с импульсной характеристикой.
h(nT) = {1.0; 0.5} и x(nT) = {0.5; 0.5}
a) расчет энергии Wy во временной области.
Определяем y(nT) с помощью круговой свертки.
N1 = 2; N2 = 2; N = N1 + N2 –1 = 3
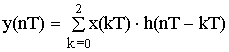
h(nT) = {1; 0.5; 0} 
x(nT) = {0.5; 0.5; 0}
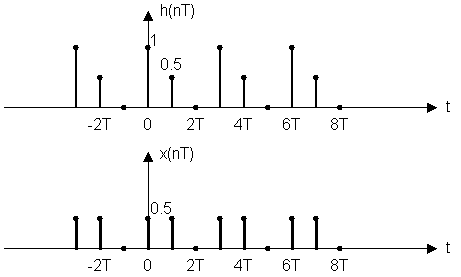
n = 0 y(0T) = x(0T)·h(0T) + x(1T) ·h(-1T) + x(2T) ·h(-2T) =
= 0.5·1 + 0.5·0 + 0·0 = 0.5
n = 1 y(1T) = x(0T) ·h(1T) + x(1T) ·h(0T) + x(2T) ·h(-1T) = 0.75
n = 2 y(2T) = x(0T) ·h(2T) + x(1T) ·h(1T) + x(2T) ·h(0T) = 0.25
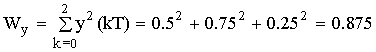
b) расчет энергии Wy в частотной области.
С помощью равенства Парсеваля определяем частотные отсчеты выходного сигнала по формуле прямого ДПФ.
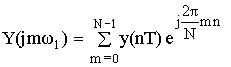
m = 0 Y(j0ω1) = y(0T) + y(1T) + y(2T) = 1.5
m = 1 Y(j1ω1) = y(0T)ej 0 + y(1T)e–j 120 + y(2T)e–j 240 = –j0.435
m = 2 Y(j2ω1) = y(0T)ej 0 + y(1T)e–j 240 + y(2T)e–j 480 = j0.435
Y(j0ω1) = {1.5; –j0.435; j0.435}
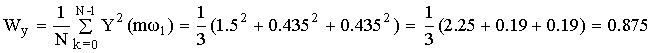
с) расчет энергии сигнала Wy по корреляционным функциям Sx(nT) и Sh(nT).
x(nT) = {0.5; 0.5}; h(nT) = {1.0; 0.5}
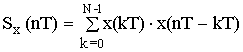
N1 = 2; N2 = 2; N = N2 + N1 – 1 = 3
x(nT) = {0.5; 0.5; 0}
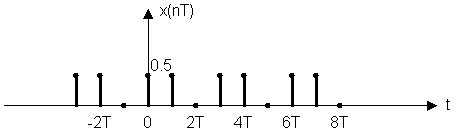
n = 0; Sx(0T) = x(0T)·x(0T) + x(1T) ·x(1T) + x(2T) ·x(2T) =
= 0.5·0.5 + 0.5·0.5 + 0·0 = 0.5
n = 1; Sx(1T) = x(0T)·x(1T) + x(1T) ·x(2T) + x(2T) ·x(3T) = 0.25
n = 2; Sx(2T) = x(0T)·x(2T) + x(1T) ·x(3T) + x(2T) ·x(4T) = 0.25
Sx(nT) = {0.5; 0.25; 0.25}
Sh(nT) = {1.25; 0.5; 0.5}
N1 = 3; N2 = 3; N = N1 + N2 – 1 = 5
Периоды корреляционных функций, участвующих в свертке, нужно увеличить таким образом, чтобы четный характер корреляционной функции сохранился.
Исходная периодическая последовательность для Sx(nT) (период =3)
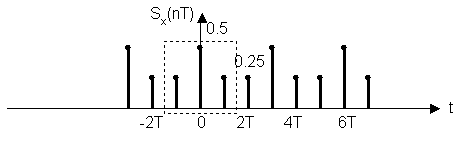
Последовательность после увеличения периода (период = 5):
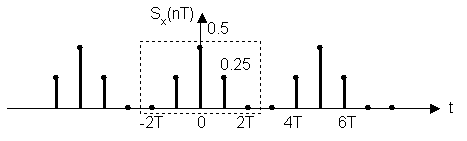
В результате выравнивания периода получаем:
Sx(nT) = {0.5; 0.25; 0; 0; 0.25}
Sh(nT) = {1.25; 0.5; 0; 0; 0.5}
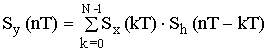
n = 0; Sy(0T) = Wy = Sx(0T)·Sh(0T) + Sx(1T)·Sh(-1T) + Sx(2T)·Sh(-2T) +
+ Sx(3T)·Sh(-3T) + Sx(4T)·Sh(-4T) = 0.5·1.25 + 0.25·0.5 + 0·0 + 0·0 + 0.25·0.5 =
= 0.625 + 0.125 + 0.125 = 0.875
Wy = 0.875
17. Цифровые фильтры
Цифровая система для обработки сигнала.
Цифровая форма реализации дискретной цепи называется цифровым фильтром.
В цифровом фильтре в отличие от дискретной цепи действия над отсчетами заменяются соответствующими цифрами, которые представлены в виде кодовых слов (нули, единицы).
Структура цифровой системы для обработки сигнала.
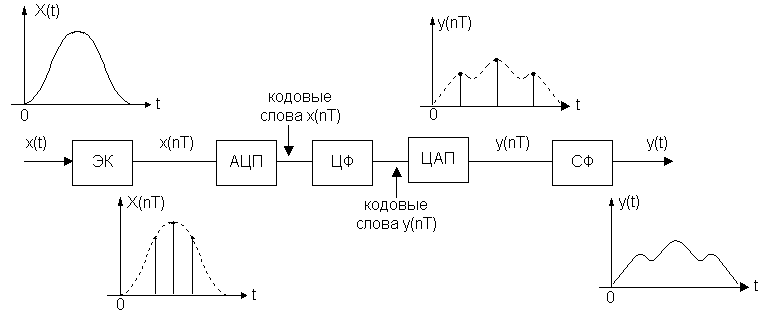
ЭК – электронный ключ
АЦП – аналого-цифровой преобразователь
ЦФ – цифровой фильтр
ЦАП – цифро-аналоговый преобразователь
СФ – синтезирующий фильтр (ФНЧ)
Цифровая схема как и дискретная схема описывается теми же уравнениями. Отличие цифровой структуры состоит в том, что сигнал на выходе отличается от идеального варианта на величину уровня шумов квантования.
Применение вычислительной техники позволяет получить высокое качество обработки сигнала, несмотря на наличие шумов квантования. Шумы квантования можно минимизировать не только увеличением длины кодовых слов, но и путем рационального конструирования цифровой схемы.
Расчет рекурсивных и не рекурсивных цифровых фильтров имеет свои особенности, поэтому расчеты этих фильтров будем рассматривать отдельно.
18. Расчет не рекурсивного ЦФ общего вида
Каноническая схема:
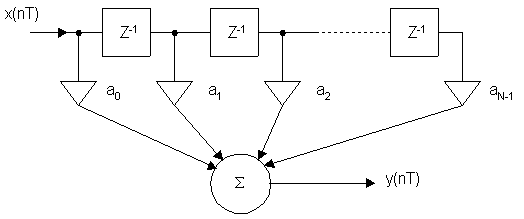
N – число отводов фильтра
Различают расчет не рекурсивного ЦФ во временной области (по импульсной характеристике), и в частотной области (по частотной характеристике).
а) Расчет фильтра во временной области.
Требуемая импульсная характеристика имеет как правило бесконечную протяженность, поэтому приходится ограничивать импульсную характеристику первыми N отсчетами.
Отбрасываемые отсчеты определяют погрешность, которую можно оценить по среднеквадратическому критерию близости.
h(nT) = {a0; a1; a2; …aN-1}
Коэффициенты проектируемого фильтра принимаются равными соответствующим отсчетам импульсной характеристики.
В заключении расчета фильтра выполняются расчеты шумов квантования, погрешностей оптимального динамического диапазона.
б) Расчет фильтра в частотной области.
В начале расчета требуемые частотные характеристики надо продолжить на диапазон [0.5ωg; ωg] по принципу комплексно-сопряженной симметрии.
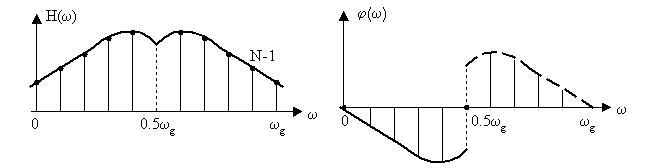
Надо задаться значением N и определить отсчеты частотной характеристики.
После выполнения всех расчетов значение N уточняется.
Определить расчеты h(nT) можно по формуле:
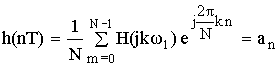
Таким образом, значение коэффициентов фильтров становится известным, после этого находим выражение для передаточной функции фильтра H(Z) и выполним проверку.
В отсчетные моменты реализуемые и требуемые характеристики совпадают, а между отсчетами не совпадают. Отличие тем меньше, чем больше N.
19. Фильтры с линейной фазой
Не рекурсивные фильтры позволяют получить четную или нечетную импульсную характеристику и как результат – линейную фазу, потому что у четных и нечетных сигналов спектр фаз строго линейный.
Рассмотрим различные варианты фильтров с линейной фазой.
1. Симметричные фильтры.
а) N – нечетное (N=5 отводы)
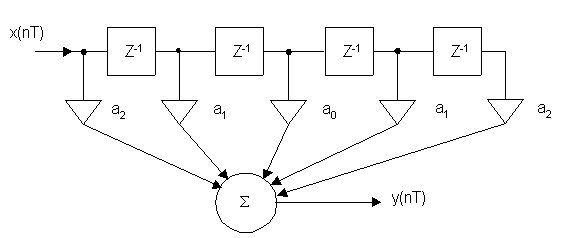
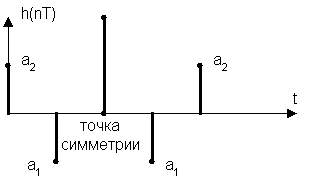
H(Z) = a2 + a1Z–1 + a0Z–2 + a1Z–3 + a2Z–4 = Z–2 [a0 + a1(Z + Z–1) + a2(Z–2 + Z2)]
Z = ejωT
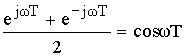
АЧХ – функция четная относительно 0.5ωg (т.к. cos – четн.).
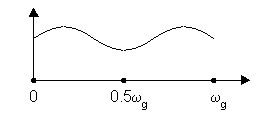
б) N – четное (N = 4)
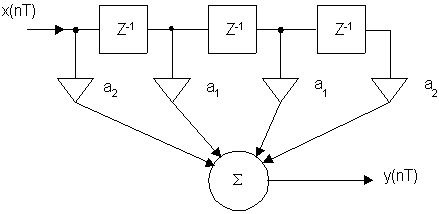
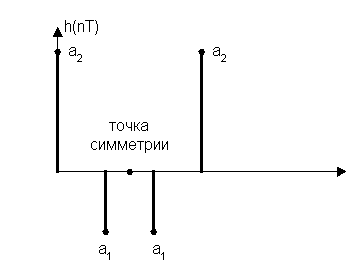
H(Z) = a2 + a1Z–1 + a1Z–2 + a2Z–3 = Z–1. 5 [a1(Z0. 5 + Z–0. 5) + a2(Z1. 5 + Z-1. 5)]
Z = ejωT
φ(ω) = -1.5ωТ функция четная, т.к: cos0.5ωT + cos1.5ωT– функция нечетная.
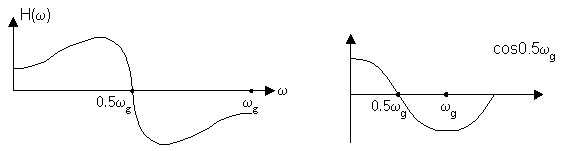
2. Антисимметричные фильтры.
а) N – нечетное (N = 5)
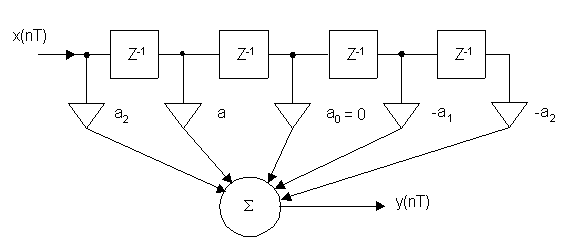
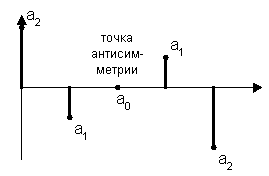
H(Z) = a2 + a1Z–1 + a0Z–2 – a1Z–3 – a2Z–4 = Z–2 [a1(Z–1 – Z–1) + a2(Z2 – Z–2)]
Z = ejωT
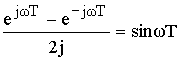
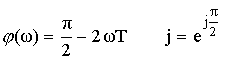
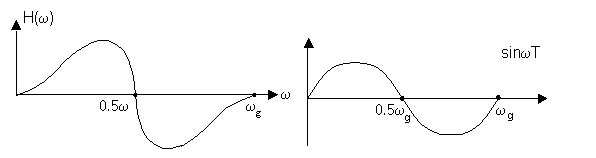
Функция нечетная.
б) N – четное (N= 4)
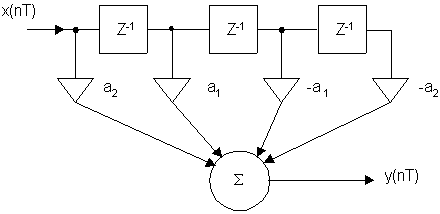
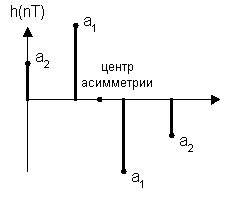
H(Z) = a2 + a1Z–1 – a1Z–2 – a2Z–3 = Z–1. 5 [a1(Z0. 5 – Z–0. 5) + a2(Z1. 5 – Z-1. 5)]
Z = ejωT
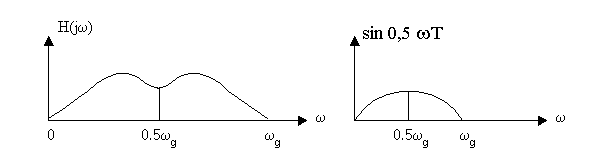
Функция φ(ω) четная, т.к. sin0.5ωT и sin1.5ωT – четные.
20. Общие свойства фильтра с линейной фазой
Анализ различных вариантов фильтров с линейной фазой позволяет выделить ряд общих свойств:
1. для симметричных фильтров
H(ω) – четн., если N нечет. 
H(ω) – нечетн., если N четн. 
2. для антисимметричных фильтров
H(ω) – четн., если N четн. 
H(ω) – нечетн., если N нечетн. 
На основании общих свойств можно сформулировать рекомендации при проектировании фильтров с линейной фазой.
1. Если 
, то фильтр симметричный;
Если 
, то фильтр антисимметричный;
2. Если 
, то АЧХ – четная, т.е. N – нечетн. для симметричных фильтров и N – четн. для антисимметричн. фильтров.
Если 
, то АЧХ – нечетная, т.е. N – четн. для симметричных фильтров и N – нечетн. для антисимметричн. фильтров.
3. Учитывая свойства фильтров с линейной фазой, АЧХ нужно продолжить на диапазон [0.5ωg; ωg] следующим образом:
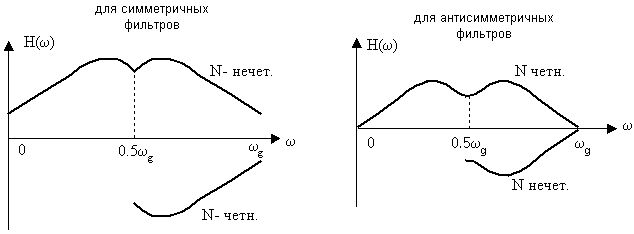
4. Антисимметричные фильтры применяются чаще в тех случаях, когда требуемая передаточная функция содержит мнимую единицу j (дифференциатор) в качестве множителя.
H(jω) = jω
H(ω) = ω
21. Расчет фильтров с линейной фазой
Расчет осуществляется по общим правилам расчета нерекурсивных фильтров, но нужно учитывать общие свойства фильтров с линейной фазой.
Пример: Рассчитать ФНЧ с линейной фазой.
ПП = [0; 200] Гц
Переходные области [200; 300] Гц
Решение:
Выбираем fg = 800 Гц ;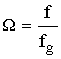 
; ПП [0; 0.25] ;
переходная область [0.25; 0.375]
Пусть N = 8
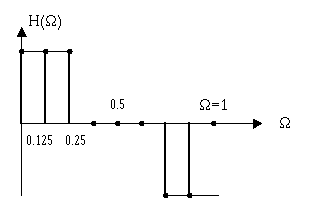
Фильтр симметричный, т.к. H(0) = 1
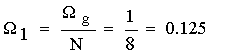отсчеты АЧХ
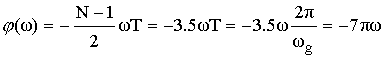отсчеты ФЧХ
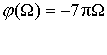
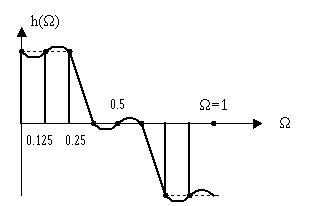
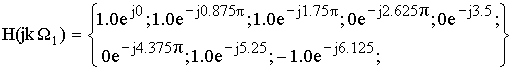
Применим формулу обратного ДПФ.
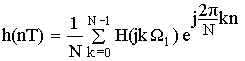= {0.065; -0.165; -0.025; 0.53; 0.53; 0.025;
-0.165; 0.065}
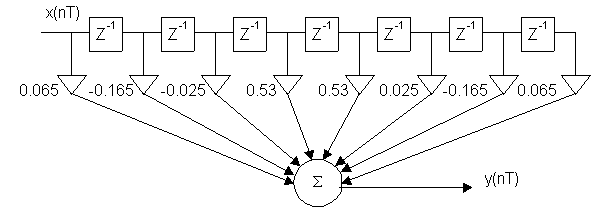
H(Z) = 0.065 – 0.165Z–1 + 0.025Z–2 +0.53Z–3 + 0.53Z–4 +0.025Z–5 –
– 0.165Z–6 – 0.065Z–7
H(Z) = Z–3. 5 [0.53(Z0. 5 + Z–0. 5) + 0.025(Z1. 5 + Z–1. 5) – 0.165(Z2. 5 + Z–2. 5) +
+ 0.065(Z3. 5 + Z–3. 5)]
H(jΩ) = e–7 πΩ(1.06cosπΩ + 0.05cos3πΩ – 0.33cos5πΩ + 0.13cos7πΩ)
Чтобы улучшить аппроксимацию требуемой характеристики АЧХ вблизи точек разрыва применяют весовую функцию (W(nT)) – сглаживающее окно.
В качестве примера рассмотрим окно Хеминга W(nT).
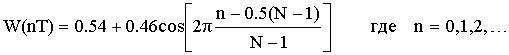
Применим окно Хеминга в нашем примере:
Рассчитываем отсчеты окна:
W(nT) = {0.08; 0.244; 0.64; 0.96; 0.96; 0.64; 0.244; 0.08}
(nT) = {0.005; –0.04; 0.016; 0.51; 0.51; 0.016; –0.04; 0.005}
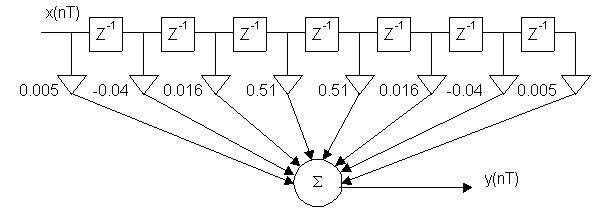
= 0.005 – 0.04Z–1 + 0.016Z–2 + 0.51Z–3 + 0.51Z–4 + 0.016Z–5 –
– 0.04Z–6 + 0.005Z–7
Отсюда получаем выражение АЧХ и строим график:
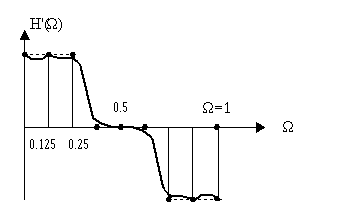
Получили меньше отклонений, применив сглаживающее окно. Эффект “сглаживающее окно” особенно эффективно для больших значений N.
Метод расчета с применением весовой функции получил название: метод взвешивания.
22. Метод частотной выборки
Схема фильтра по методу частотной выборки строится с таким расчетом, чтобы коэффициенты фильтра соответствовали частотным отсчетам частотной характеристики.
а) Схема фильтра получается путем эквивалентных преобразований передаточной функции нерекурсивного фильтра.
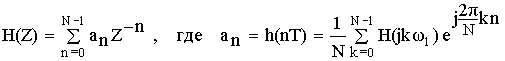
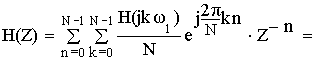
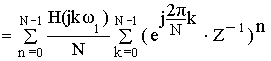
Применим :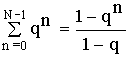 
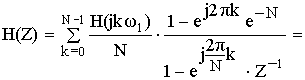
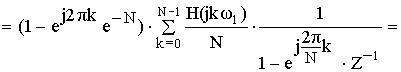
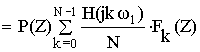
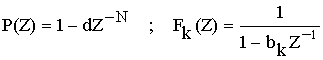
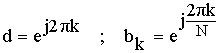
В соответствии с полученным результатом схема нерекурсивного фильтра примет следующий вид:
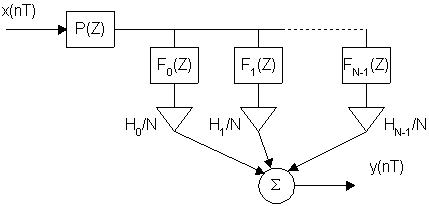
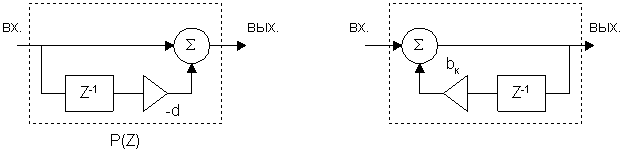
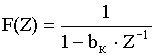
Нули и полюсы полученной передаточной функции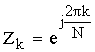 
совпадают и расположены на единичной окружности плоскости Z. Чтобы исключить возможность самовозбуждения, нули и полюсы целесообразно сместить внутрь единичной окружности на малую величину.
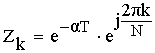– новое положение нуля и полюса.
Требуемое смещение нулей и полюсов функции получаем за счет некоторого изменения коэффициентов dи bK.
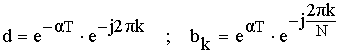
b) Частотная характеристика фильтра.
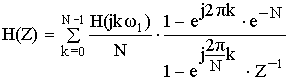
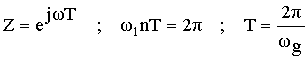
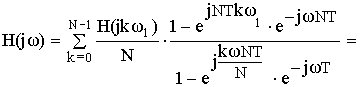
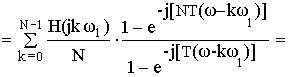
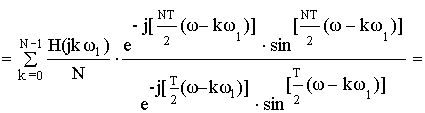
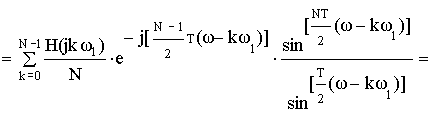
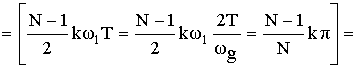
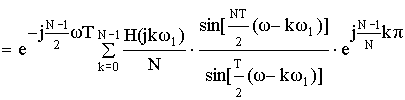
Частотная характеристика фильтра по методу частотной выборки получилась в форме ряда Котельникова для спектров дискретных сигналов, т.е. частотная характеристика состоит из суммы отсчетных функций, причем регулировка амплитуды каждой из отсчетнной функции не влияет на амплитуду других отсчетных функций.
Рассмотрим формирование суммы отсчетных функции на примере некоторой АЧХ.
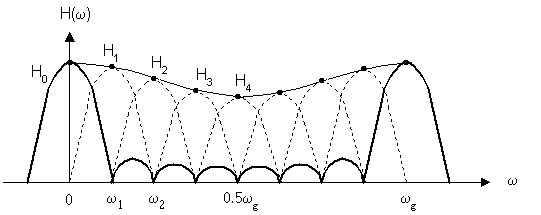
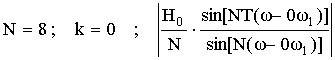
в) Схема фильтра с вещественными отводами.
Передаточная функция отводов k и N-k является комплексно-сопряженной, потому что частотная характеристика удовлетворяет условию комплексно-сопряженной симметрии.
Объединяя отводы k и N-k, мы получим один отвод с вещественными коэффициентами.
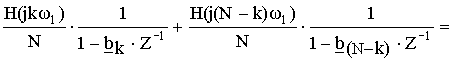
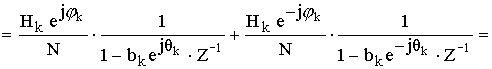
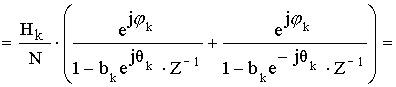
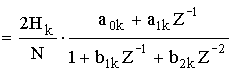
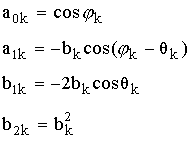
Полученному выражению соответствует схема:
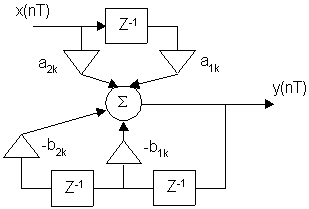
Схема с вещественными отводами получила преимущественное распространение. Важное достоинство: в схеме фильтра отсутствуют комплексные отводы соответствующие нулевым значениям требуемой частотной характеристики.
23. Расчет рекурсивных фильтров
При расчете рекурсивных фильтров применяются прямые и косвенные методы.
Косвенные методы предполагают в качестве промежуточного этапа расчет аналогового фильтра (АФ). Затем по передаточной функции АФ получают схему цифрового фильтра (ЦФ).
Метод билинейного преобразования.
Основой этого метода является такое преобразование частоты, при котором частотная характеристика АФ сжимается до конечных размеров. В результате ошибок наложения, которые всегда существуют при переходе от АФ к ЦФ, частотные преобразования осуществляются с помощью выражения:
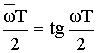где 
ω – реальная частота (частота ЦФ). Тогда: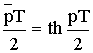 
Соотношение между реальной и расчетной частотой удобно изобразить на графике.
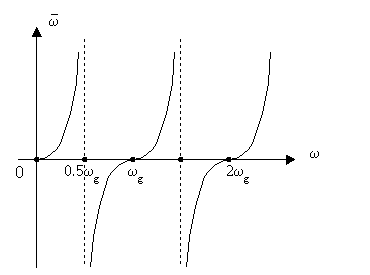
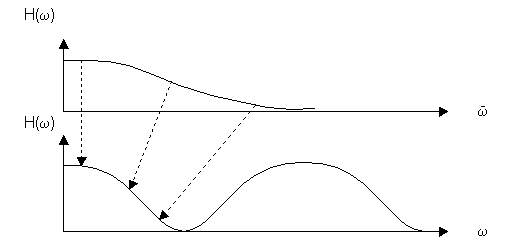
Рассмотрим графически, как преобразуется частотная характеристика АФ в частотную характеристику ЦФ.
Рассмотрим соотношение частот pи 
по отношению к Z-плоскости.
Соотношение между P и Z:
Соотношение между 
и Z-плоскостью:
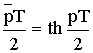, тогда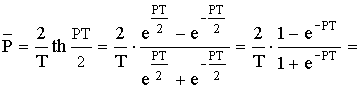 
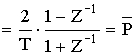
Последовательность расчета по методу билинейного преобразования.
1) Задано: норма на АФ переходит на ЦФ.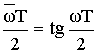 
2) Рассчитать АФ в соответствии с полученными нормами. В результате расчетов становится известной передаточная характеристика H(
).
3) Определить H(Z) по H(
) применяя формулу: 
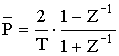
4) По передаточной функции H(Z) построить схему ЦФ.
5) Выполнить нужные расчеты по учету эффекта конечных разрядностей.
Недостаток метода в том, что преобразование частот носит нелинейный характер. Метод применяется, в основном, при проектировании частотно–селективных фильтров.
Пример:
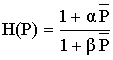
Решение: определим H(Z) подстановкой
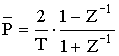
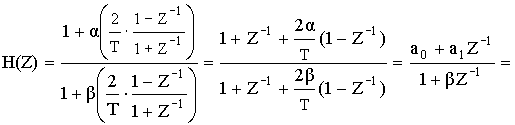
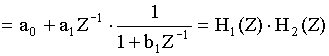
24. Эффекты конечной разрядности и их учет
Шумы квантования и шумовая модель.
Отсчеты сигнала в АЦП округляются к ближайшему разрешенному уровню. Расстояние между смежными уровнями квантования равно шагу квантования Δ. В результате кодовые слова имеют конечную разрядность после округления (b – разрядность кодовых слов). Значение младшего разряда кодового слова равно шагу квантования.
Δ и b связаны соотношением:
Δ = 2 -b
Разность между истинным отсчетом и квантованным результатом:
e(nT) = e(n) – ошибка квантования.
Ошибка квантования определяется неравенством:
при округлении результата.
при усечении результата.
Квантование происходит не только в АЦП, но и в умножителе т.к. при умножении кодовых слов разрядность результата равна сумме разрядностей множимого и множителя.
Ошибки округления на выходе цифрового фильтра воспринимаются в виде шума, который называется шумом квантования.
Расчет шумов квантования на выходе ЦФ осуществляется по шумовой модели, которая отличается от исходной цепи наличием источников шума.
Пример:
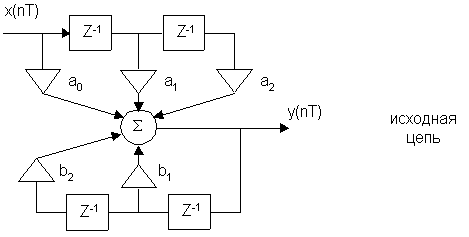
e0(n) – шум от АЦП
ei(n) – шум от умножителя
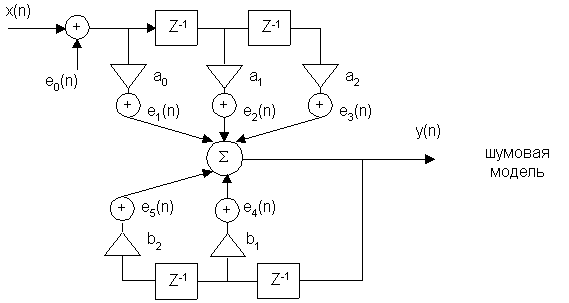
Расчет шумов квантования.
Оценку шума можно выполнить по максимуму шума или усредненной энергии шума:
1. первая оценка соответствует наихудшему случаю,
2. вторая оценка соответствует условию вероятностного подхода к решению задачи.
Расчет максимального шума.
Шум на выходе цепи eiвых(n) определяют по формуле свертки:
где: ei(k) – шум на выходе i-го источника шума;
hi (n) – импульсная характеристика участка цепи от выхода i-го источника шума до выхода цепи.
Maксимум шума на выходе цепи ei вых max (n) = Eiвозникает в случаях:
1. когда ei (k) и hi (n-k) имеют одинаковые знаки;
2. когда на выходе i-го источника наблюдается max шума.
при округлении
eimax(n) = Δiпри усечении
Тогда max шума на выходе цепи:
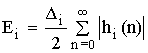при округлении.
Maxшума на выходе цепи от всех источников при условии наихудшего случая будет наблюдаться тогда, когда maxшума на выходе цепи от всех источников будут складываться.
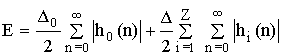
– maxшума на выходе АЦП,
– maxшума на выходе каждого из Z умножителей, если разрядность всех умножителей одинакова.
Расчет уровня шума по условию наихудшего случая приводит к
тому, что уровень реального шума значит меньше расчетного. Чаще применяется расчет усредненного значения.
25. Расчет усредненной энергии шума
Расчет усредненной энергии шума на выходе цепи от i-го источника шума выполняется по формуле:
где: σi2 – дисперсия шума на выходе i-го источника шума;
hi (n) – импульсная характеристика.
Шум квантования представляет собой случайную последовательность типа “белый” шум, поэтому σi2 на выходе i-го источника определяется:
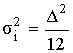при округлении чисел;
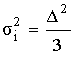при усреднении чисел.
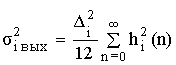
Источники шума не коррелированны между собой, поэтому усредненная энергия шума на выходе цепи от всех источников получается сложением усредненной энергии шума от каждого источника.
Усредненная энергия шума от всех источников на выходе цепи определяется по формуле:
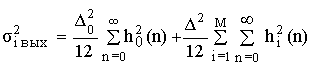
где: 
– усредненная энергия шума на выходе АЦП;
М – число ветвей цифрового фильтра;
– усредненная энергия шума на выходе каждого из Z-умножителей, если разрядность всех умножителей одинакова.
Расчет уровня шума по условию вероятностной оценки вполне удовлетворительно соответствует реальному уровню шума, но в этом случае не исключены кратковременные скачки уровня реального шума по отношению к расчетному.
26. Влияние структуры цепи на шум квантования
Если в передаточной функции некоторой цепи имеются высокодобротные полюсы, то отсчеты импульсной характеристики этой цепи медленно убывают с ростом номера отсчета, поэтому шум квантования оказывается значительным. Уровень шума такой цепи можно понизить, применяя каскадную реализацию цепи.
Каскадная реализация цепи начинается с синтеза передаточной функции в виде произведения простейших сомножителей.
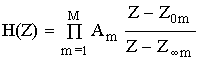
где: Z0m – нули H(Z);
Z∞m – полюсы H(Z).
Нули и полюсы группируются в пары по принципу: каждому полюсу подбирается ближайший расположенный к нему ноль.
Сомножителям первого порядка (нули, полюсы вещественные) соответствуют звенья первого порядка. Сомножителям второго порядка (нули, полюсы комплексно-сопряженные) соответствуют звенья второго порядка.
Звенья располагаются в порядке возрастания добротности. Добротность комплексных полюсов для плоскости Z определяется:
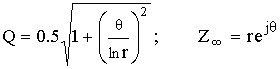
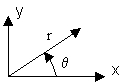
– угол (частота) полюса;
r – радиус полюса.
В качестве формулы добротности воспользуемся анализом:
Q = r
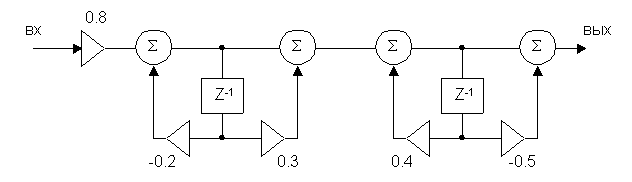
Пример: осуществить каскадную реализацию передаточной функции.
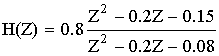
Z2 – 0.2Z – 0.15 = 0
Z2 – 0.2Z – 0.08 = 0
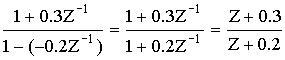
27. Квантование коэффициентов
Специализированный процессор, предназначенный для обработки сигналов, будет тем эффективней (экономически), чем короче кодовые слова. Кодовые слова коэффициентов имеют конечную разрядность, т.к. при переходе от расчетных значений к двоичному представлению коэффициента кодовые слова получаются бесконечной разрядности, поэтому бесконечную разрядность приходится ограничивать.
Чем меньше разрядность коэффициента, тем больше погрешность синтезируемых характеристик. Поэтому квантовать коэффициенты надо с таким расчетом, чтобы не превысить допуск на отклонение синтезируемых характеристик.
При переходе к двоичному числу целая часть числа будет изображать знак, причем: “1” будет стоять в целой части, если знак “–”,
“0” будет стоять в целой части, если знак “+”.
Дробная часть числа характеризует модуль числа.
Пример:
Дано десятичное число с фиксированной запятой.
A(10) = 0.32 определить A(2) = ?
A(2) = 0010100011 Разрядность 8 кодовых слов
| -0.32 | 0.64 | 1.28 | 0.56 | 1.12 | 0.24 | 0.48 | 0.96 | 1.92 | 1.84 |
A(2) = 0.010100100 => A(2) = 0.01010010 при округлении
A(2) = 0.010100011 => A(2) = 0.01010001 при усреднении
Для оценки погрешности выполним обратный переход к A(10)
При округлении A(10) @ 0·2 – 1 + 1·2 – 2 + 0·2 – 3 + 1·2 – 4 + 0·2 – 5 + 0·2 – 6 +
+ 1·2 – 7 + 0·2 – 8 = 0.3203125
Δ – абсолютная погрешность
Δ = 0.3203125 – 0.32 = 0.0003125
–относительная погрешность.
При усечении A(10) @ 0.31640625
Δ = 0.32 – 0.31640625 = 0.00359375
Для расчета разрядности существуют различные методы, самый простой – метод проб.
Последовательность расчета по методу проб.
1. задаться разрядностью коэффициента ориентировочно (8,10);
2. рассчитать новые значения коэффициентов для выбранной разрядности;
3. рассчитать системные характеристики цепи с новыми коэффициентами цепи;
4. оценить погрешность системных характеристик;
5. изменить разрядность коэффициентов в ту или иную сторону, в зависимости от погрешности системных характеристик и повторить расчет.
28. Масштабирование сигнала в цепи
Шум квантования на выходе цифровой цепи не зависит от уровня сигнала. Чем выше уровень сигнала в цепи, тем лучше соотношение сигнал/шум. Но высокие уровни сигнала могут привести к переполнению (перегрузке) сумматора, т.е. к выходу числа за пределы разрядной сетки слева.
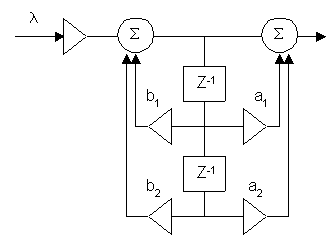
Чтобы получить нужный уровень применяется масштабирование сигнала. С этой целью на входе цепи устанавливают умножитель с коэффициентом умножения λ.
Для расчета λ используют различные методы.
1. Расчет λ по условию ограничения максимума сигнала.
Сигнал на выходе i-го сумматора, т.е. yi (n) можно рассчитать применением свертки:
Условия maxсигнала yi(n)
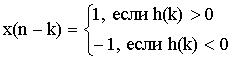
Учитывая эти условия получим формулу для максимально возможного сигнала на выходе сумматора.
Потребуем, чтобы maxyi(n) = 1
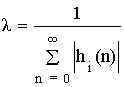
Расчет λ выполняется по каждому сумматору. Из всех λ выбирается наименьшее и округляется в меньшую сторону до ближайшего числа кратного степени 2, что позволяет осуществить умножение простым сдвигом числа в числовом регистре.
Расчет λ по условию max сигнала приводит к низким уровням сигнала цепи, поэтому расчет λ часто выполняется по условию ограничения энергии сигнала.
2. Расчет λ по условию ограничения энергии сигнала.
Расчет энергии сигнала на выходе i-го сумматора определяется:
формула справедлива для случайного
сигнала с равномерным энергетическим спектром, что соответствует реальному сигналу.
Энергия сигнала на выходе i-го сумматора равна энергии сигнала на входе, т.е. Wyi = Wx. В результате исходная формула примет вид:
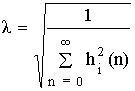
Уровень сигнала цепи получается выше, но здесь не исключена возможность перегрузки сумматора (но вероятность перегрузки мала).
3. Расчет λ по условию ограничения максимума усиления цепи.
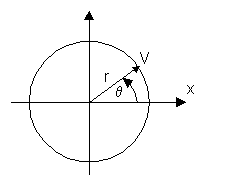
Спектр сигнала на выходе i-го сумматора определяется:
Если ω∞ – частота максимального усиления сигнала, то условие максимума усиления сигнала запишется:
где: ω∞ – частота высокодобротного полюса
– коэффициенты высокодобротного полюса.
Потребуем, чтобы Y(ω∞) = X(ω∞), тогда выражение для максимального спектра выходного сигнала принимает вид:
1 = λ H(ω∞)
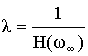
Расчет λ приводит к значениям λ, где–то между случаями 1 и 2. Расчет λ в этом случае применяется для каскадной реализации, когда масштабирование осуществляется внутри каждого звена, за счет чего масштабирование получается очень эффективным.
29. Оценка эффективности использования динамического диапазона цепи
Масштабирование позволяет повысить эффективность использования динамического диапазона. Динамический диапазон цепи определяется границами выходного сигнала [Δ; 1.0] применительно к числам фиксированной запятой.
Δ – значение младшего разряда кодового слова.
Эффективность использования динамического диапазона определяется с одной стороны значением вероятности перегрузки сумматоров, и помехозащищенностью Rш сигнала с другой стороны.
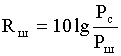
Pc– мощность сигнала на выходе цепи
Pш – мощность шума на выходе цепи
Рассчитать Rш можно и подругому, учитывая равенство:
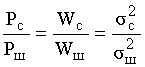
30. Предельные циклы
Предельными циклами называют ложные сигналы, которые возникают на выходе цепи, если на вход поступает сигнал в виде константы.
Предельные циклы появляются на выходе цепи вследствии ограничения разрядности кодовых слов на выходе умножителей.
Пример:
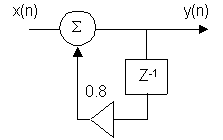
Определить форму и величину предельных циклов, если в последовательности x(n) в момент времени t=0 наступила пауза. При этом Y(–1) = 0.5, учитываем, что значение сигнала на выходе цепи ограничивается десятыми долями.
y(n) = x(n) + 0.8y(n – 1)
n=0 y(0) = 0 + 0.8·0.5 = 0.4
n=1 y(1) = 0 + 0.8·0.4 = 0.32 @ 0.3
n=2 y(2) = 0 + 0.8·0.3 = 0.21 @ 0.2
n=3 y(3) = 0 + 0.8·0.2 = 0.16 @ 0.2
n=4 y(4) = 0 + 0.8·0.2 = 0.16 @ 0.2
y(n) = {0.4; 0.3; 0.2; 0.2; 0.2…}
Если коэффициент (0.8) заменить на (–0.8), то на выходе получим:
y(n) = {–0.4; –0.3; –0.2; –0.2; –0.2…}
Предельный цикл становится знакопеременным.
Для цепи высокого порядка предельные циклы имеют сложную форму, которые трудно поддаются теоретическому анализу. При проектировании цифровых фильтров величина и форма предельных циклов выявляется результатом моделированием на ЭВМ.
31. Чувствительность цифровых фильтров
Чувствительностью величины m по параметру q называют соотношение:
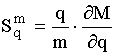
Чувствительность показывает на сколько процентов изменится величина m, если параметр q изменится на 1%.
Для цифровой цепи часто в качестве величины m берут частотную характеристику.
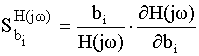
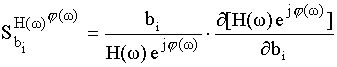
После дифференцирования получаем формулу чувствительности АЧХ и ФЧХ.
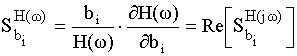– чувствительность АЧХ
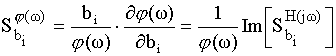– чувствительность ФЧХ
Пример:
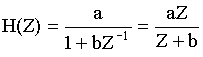
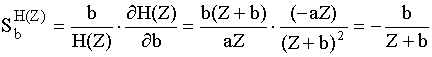
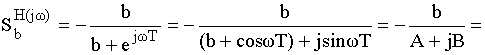
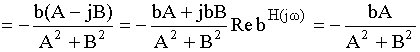
Полученная частотная зависимость показывает на сколько процентов изменится АЧХ на каждой частоте, если коэффициент b изменился на 1%.
32. Быстрое преобразование Фурье
При цифровой обработке для повышения скорости обычно используют дискретное преобразование Фурье. Для частотного представления сигнала требуется большое количество операций умножения.
В 1965г изобретено быстрое преобразование Фурье, существенно уменьшающее количество операций умножения.
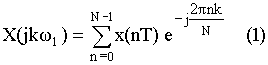прямое преобразование Фурье.
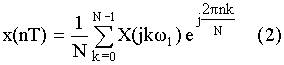обратноe преобразование Фурье.
При прямом преобразовании Фурье:
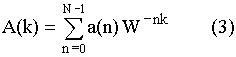; где 
При обратном преобразовании Фурье:
Для вывода БПФ заменим прямое и обратное преобразование Фурье формулой (3), где:
a(n) – сигналы отсчета во временной области,
A(k) – отсчеты в частотной области исследуемого сигнала.
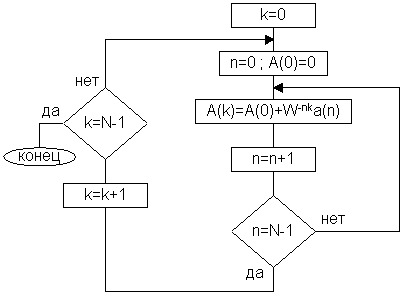
Проанализируем общий алгоритм вычисления ДПФ и обратного ДПФ.
Qобщ – операции умножения
Qобщ = N2
При вычислении весов функции 
, много значений этой функции дублируется, а именно, при вычислении N точечного вычисления ДПФ, 
значений W оказываются лишними. Проанализируем поведение весов. функции для N=8.
N=8 W0 = 1
При анализе поведения весовой функции видна следующая закономерность: 
значений весовой функции (первые значения равны следующим 
весовой функции, взятых со знаком “–”).
|
nk |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
W-nk |
1 |
W-1 |
W-2 |
W-3 |
-1 |
-W-1 |
-W-2 |
-W-3 |
Используем свойство весовой функции для уменьшения операций умножения. Для этого разобьем последовательность прямого преобразования Фурье на четные и нечетные составляющие.
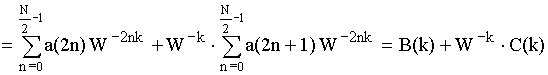
Для получения восьмиточечного ДПФ, исходя из ниже следующей формулы, воспользуемся следующей структурой:
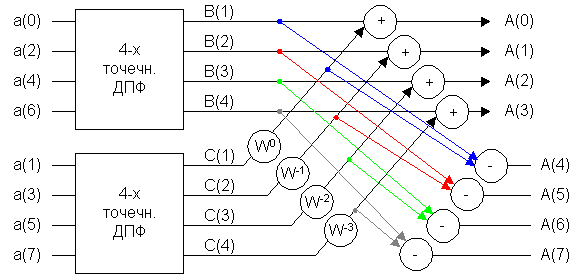
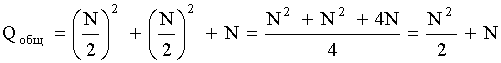
Исходя из преобразования 4-х точечного ДПФ, сделаем преобразование до 2-х точечного ДПФ. Тогда структура будет следующая:
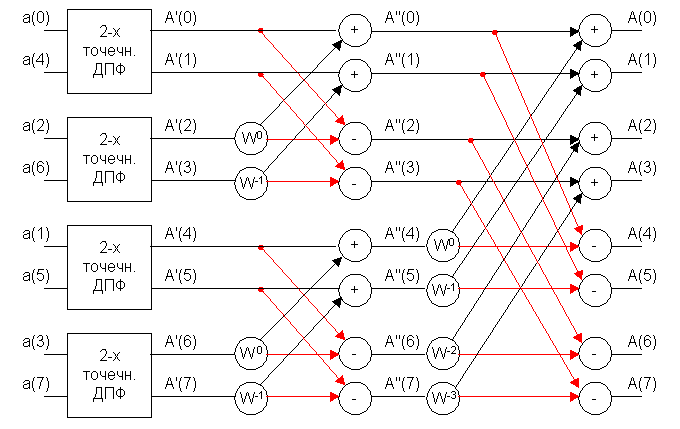
При преобразовании 8-ми точечного ДПФ в 2-х точечное существенно сокращается количество умножений. Первая стадия преобразования 2-х точечного ДПФ вырождается в структуру:
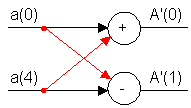
Структура БПФ предполагает замену операции умножения на операцию суммирования или вычитания. При выполнении операции суммирования или вычитания требуется существенно меньше времени, чем для операции умножения.
Для реализации БПФ отсчеты подлежащие преобразованию должны подаваться в инверсно–кодированной форме.
|
“n”текущ. |
000 |
001 |
010 |
011 |
100 |
101 |
110 |
111 |
|
БПФ |
000 |
100 |
010 |
110 |
001 |
101 |
011 |
111 |
При представлении сигнала в инверсно–кодированной форме, получаем эквивалентный зеркальный переворот значений разрядов. Там, где отсчеты располагаются симметрично, никакого преобразования не надо.
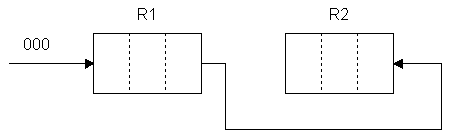
При инверсно–кодированных операциях необходимо зеркально отобразить исходную последовательность номеров. Реализация с помощью аппаратных средств производит перекодирование в двоично-инверсную последовательность.
|
N0такта |
P1 |
P2 |
P3 |
N0такта |
P1 |
P2 |
P3 |
|
1 |
0 |
4 |
¬0 |
||||
|
2 |
0 |
0 |
5 |
0 |
0 |
||
|
3 |
0 |
0 |
0 |
6 |
0 |
0 |
0 |
На вход регистра R1 подавалась кодовая комбинация из трех нулей. После шести тактов в регистре R2 будет также последовательность состоящая из трех нулей.
|
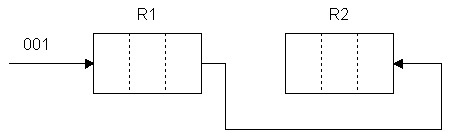
N0такта |
P1 |
P2 |
P3 |
N0такта |
P1 |
P2 |
P3 |
|
1 |
1 |
4 |
1 |
||||
|
2 |
0 |
1 |
5 |
1 |
0 |
||
|
3 |
0 |
0 |
1 |
6 |
1 |
0 |
0 |
Если кодовые комбинации не симметричны (1, 4, 6), то они подлежат преобразованию в двоично-инверсную кодированную форму.
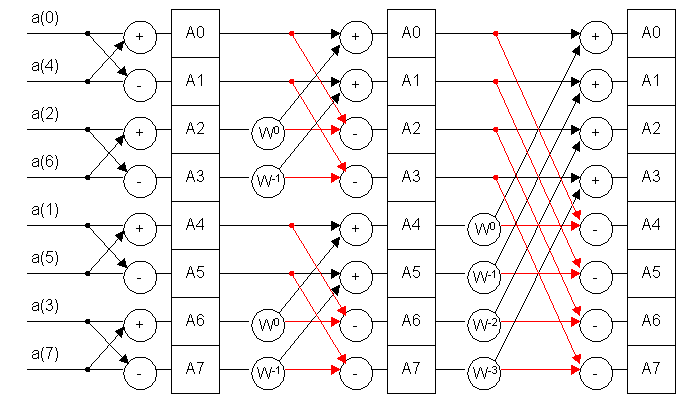
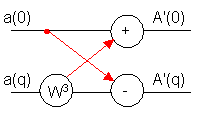
Реализация алгоритма БПФ.
После каждого этапа преобразования получается массив, который обозначается А0 – А7. Так как результаты предыдущих вычислений в дальнейших расчетах используются один раз, то вместо прежних значений А0 – А7 рассчитываются новые значения А0 – А7, таким образом уменьшается объем памяти.
На каждом этапе количество N изменяется. Чтобы упростить вычисление и сделать алгоритм общим, для всех этапов полагают N равно исходному значению отсчетов, которые подлежат преобразованию.
Пример:
С помощью БПФ рассчитать спектральный состав временной последовательности представленной в виде:
x(nT) = {1; 1; -1; -1; 1; 1; -1; -1}
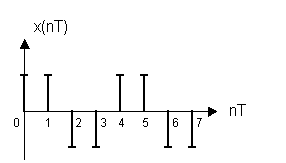
X(jkω1) = {0; 0; 4 – 4j; 0; 0; 0; 4 + 4j; ? ; 0 }
r – количество пар (
)
m – количество этапов преобразования
r – текущее значение вычисляемой пары
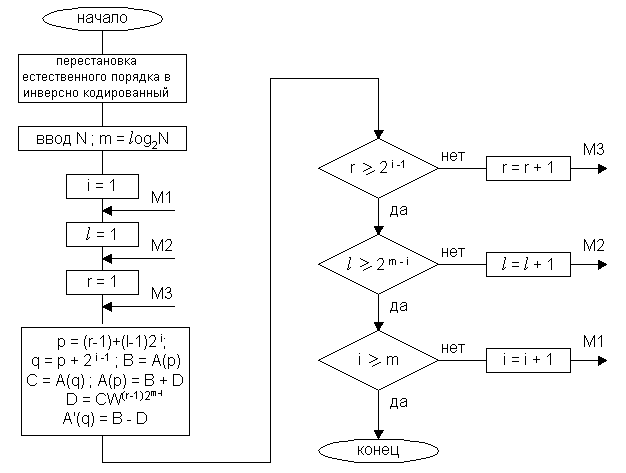
33. Алгоритм инверсно кодированных перестановок
Наряду с аппаратными средствами получения инверсно кодированных отсчетов существуют программные средства выполнения тех же самых операций.
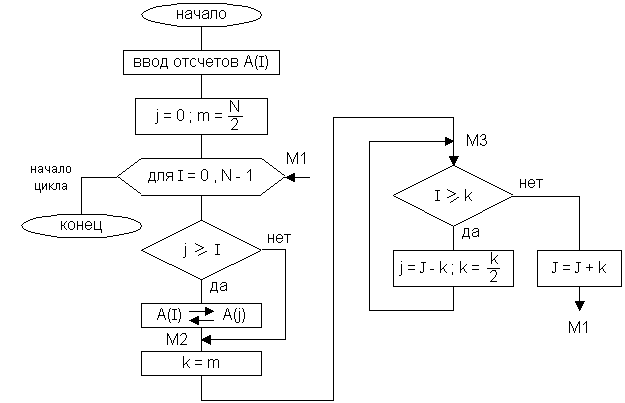
10 DIM A(N)
20 FOR I = 1 TO N
30 INPUT A(I)
40 PRINT “A(I) =”, A(I)
50 NEXT I
60 LET j = 0
70 LET 
80 LET I = 0
85 IF I > N-1 THEN GO TO 210
90 IF j < 1 THEN GO TO 140
100 LET A = A(I)
110 LET B = A(J)
120 LET M(I) = B
130 LET M(J) = A
140 LET k = m
150 IF J ≥ k THEN GO TO
160 LET J = J + k
170 GO TO 85
180 LET J = J – k
190 LET 
200 GO TO 90
210 END
10 – объявление массива входной последовательности, который подлежит преобразованию;
20 
50 – ввод входной последовательности;
60 
70 – начальное присвоение переменной J и переменной m;
80 – начало цикла расчета I = 0;
85 – проверка значения переменной I, если I > N-1, то цикл расчета продолжается;
90 – проверка условий;
100 – переприсвоение значений массива;
140 – присвоение переменной kзначений m;
150 
170 – организация цикла расчета, присвоение переменной J и k.
34. Алгоритм расчета ДПФ
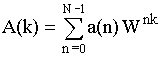
10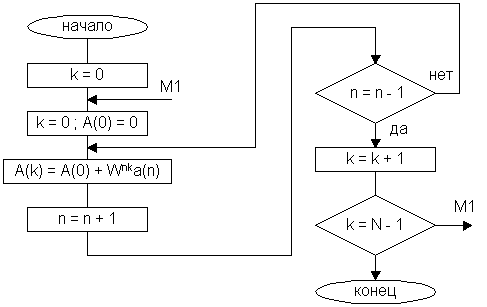 
DIM a(N)
20 DIM A(N)
30 FOR I = 0 TO N-1
40 INPUT a(I)
50 NEXT I
60 LET k = 0
70 LET n = 0
80 LET A(0) = 0
90 LET 
100 LET n = n + 1
110 IF n < N-1 THEN GO TO 90
120 LET k = k + 1
115 LET 
130 IF k < N-1 THEN GO TO 70
140 END
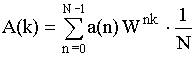
Данная программа позволяет выполнить прямое ДПФ, где:
a(n) – отсчеты сигнала во времени ;
A(k) – отсчеты спектра сигнала X(jω1k).
В случае обратного ДПФ в программе надо сделать изменения:
a(n) – отсчеты спектра X(jω1k);
A(k) – отсчеты сигнала во времени.
Каскадное включение МПК для расчета в реальном масштабе t.
При реализации цифровых фильтров одной из самых главных задач является расчет в реальном масштабе t.Он подразумевает обработку сигнала с такой же скоростью, как и поступление входных отсчетов.
y(nT) поступает с такой же скоростью, что и x(nT).
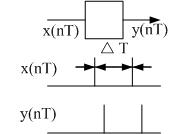
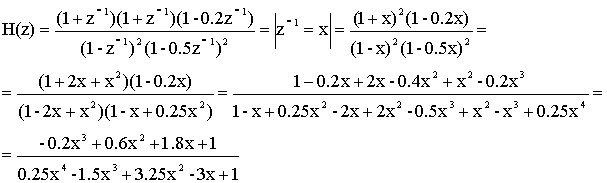
После преобразования исходного многочлена на ряд элементарных многочленов производят представление передаточной функции в виде простейших элементарных составляющих. Сначала должен располагался четырехполюсник с малой добротностью, а потом добротность возрастает.
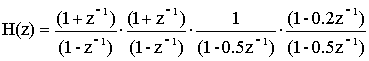
В результате разбиения H(z) на четыре элементарных передаточных характеристики: H1(z)…H4(z), время, отводимое на реализацию Hi(z), возрастает как минимум в четыре раза, этим самым производится параллельный обмен времени на аппаратурную сложность.
Преимущество: уменьшение времени расчета в каждом звене.
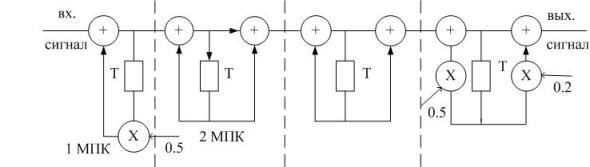
Недостаток: выходной сигнал задерживается как минимум на четыре тактовых интервала.
35. Параллельные соединения ЦФ
При синтезе последовательного ЦФ не возникает больших затруднений с получением элементарных передаточных характеристик, они получаются на основе элементарных преобразований математики.
Есть существенный недостаток: обрабатываемый сигнал задерживается на столько тактовых интервалов, сколько элементарных ЦФ мы последовательно включаем. Если не разрешается задержка обрабатываемого сигнала, то решением данной проблемы является параллельное соединение элементов четырехполюсников.
Пример:
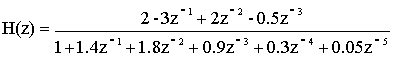
Нули: 1+j; 1-j; 2
Полюсы: -1+j; -1-j; -1+2j; -1-2j; -2
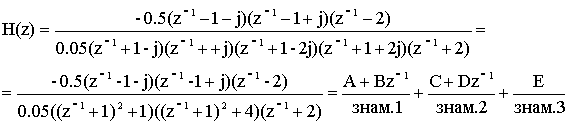
При разложении общей передаточной характеристики на три элементарных составляющих оказываются неизвестными коэффициенты A,B,C,D,E. Значения этих коэффициентов ищутся численными методами с помощью моделирования на ЭВМ.
A=16.55117
B=-8.9655
C=-2.551
D=-4.85517
E=21.10345
Знам.1=1+z-1+0.5z-2
Знам.2=1+0.4z-1+0.2z-2
Знам.3=1+0.5z-1
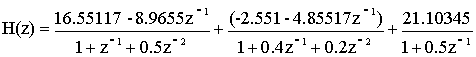
Из анализа передаточной характеристики следует:
1. выходной сигнал при прохождении через элементарные передаточные характеристики должен арифметически складываться;
2. темп поступления входных и выходных отсчетов одинаков. Выходной сигнал не задержан, в отличии от входного.
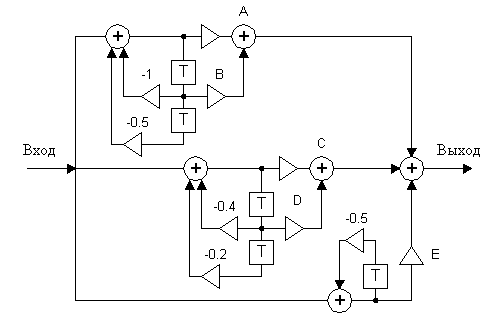
Разложение сложной передаточной характеристики либо на параллельное, либо на последовательное называется распаралелением процесса обработки. Для данного конкретного случая каждый элементарный ЦФ синтезирован на одном сигнальном процессоре.
36. Оптимальная обработка сигнала
Под оптимальной обработкой сигнала подразумевается задание исходных данных для амплитудно-частотной и фазо-частотной характеристик цифрового фильтра или аналогового фильтра.
Оптимальная фильтрация наиболее актуальна в связи с широким внедрением цифровых фильтров. Это связано с тем, что цифровой фильтр можно со сколько угодно большой точностью приблизить к рассчитанным характеристикам.
Pвх Pвых 
максимизировать
Eвх Eвых
nвх(t)-шум nвых(t)
Для выкладок будем подразумевать, следовательно, распределение входного шума равномерное.
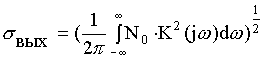
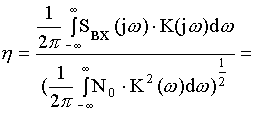
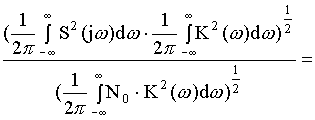
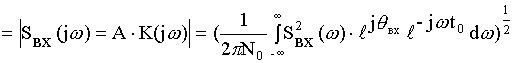
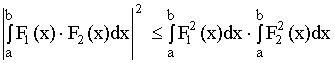
1. 
2. Фазовая характеристика складывается из входного сигнала и задержки:
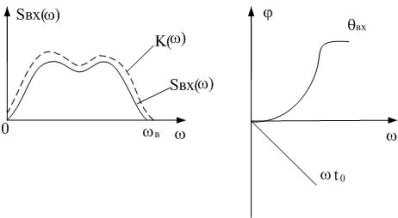
При синтезе оптимального фильтра фазовая характеристика должна быть комплексно сопряженная относительно фазовой характеристики входного сигнала.
При прохождении через оптимальный фильтр в виду того, что фазовая характеристика комплексно сопряжена с фазовой характеристикой входного сигнала, данная составляющая уничтожается.
Оптимальный фильтр не вносит фазовых искажений, его характеристика такова, что все фазовые искажения входного сигнала компенсируются.
Расчет импульсной реакции согласованного фильтра для белого шума.
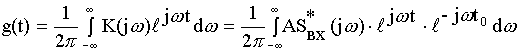
задержка
Импульсную реакцию вычислим, исходя из ОПФ. Для согласованного фильтра 
должна быть комплексно сопряжена величине входного спектра сигнала. Любой фильтр дает задержку выходного сигнала. Согласованный фильтр не вносит никаких фазовых искажений.
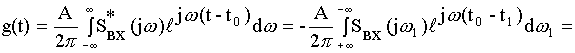
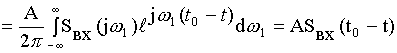
- замена
Импульсная реакция согласованного фильтра должна быть прямо пропорциональна входному сигналу во временной области, зеркально развернутому относительно оригинала согласованного фильтра. После обеливания включается каскадно четырехполюсник, у которого характеристики обратны характеристикам обелившегося фильтра.
- любая физически реализуемая цепь
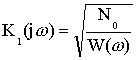
- средне-квадратическое отклонение шума
- распределение шума на выходе
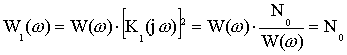- мощность шума на выходе
Функции обелившегося фильтра заключаются в том, что при прохождении через подобный фильтр свойства шума становятся подобными свойствам белого шума.
Для анализа работы согласованного фильтра нужно рассматривать не только прохождение шума, но и прохождение сигнала.
Так как распределение помехи на выходе обеляющего фильтра близко к нормальному, то тогда возможно использование математических выкладок для согласованного фильтра с белым шумом.
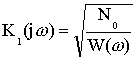
Для расчета 
воспользуемся:
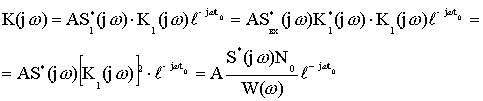
Из данного выражения следует:
1. модуль коэффициента передачи согласованного фильтра Хинчина-Винера прямо пропорционален модулю спектральной плотности входного сигнала 
и обратно пропорционален спектральной плотности шума или помехи 
2. как и в согласованных фильтрах, для белого шума фазовая характеристика обратна фазовой характеристике входного сигнала.
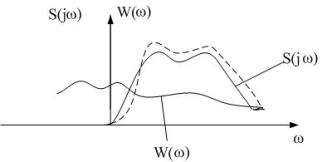
- искомая характеристика Хинчина-Винера
Приемы для синтеза согласованного фильтра Хинчина-Винера.
1. Для заданного канала рассчитывают ансамбль сигналов, при этом энергетический спектр передаваемого сигнала 
должен быть согласован с параметрами использованного канала связи.
2. Обычно экспериментально снимают помеховую обстановку, то есть с помощью каких-то устройств смотрят, как распределена помеха, затем снимают распределение помехи
.
3. На основе расчета характеристики согласованного фильтра строят модуль коэффициента передачи, исходя из общей формулы Хинчина-Винера.
4. Зная 
, с помощью ОБПФ ищут отсчеты импульсной реакции.
5. Зная 
, любым известным способом строят структуру согласованного фильтра в цифровой форме.
37. Перенос спектра сигнала в заданную область. Выделение боковой (нижней или верхней)
При синтезе систем связи с частотным разделением канала (с ЧРК) делаются следующие операции:
1. Расчет области частот среды распространения (в радиоаппаратуре - отведенная полоса частот, в кабельных линиях связи – это полоса частот от минимально разрешенной до максимально разрешенной для данной аппаратуры, для оптоволоконных линий – это окно прозрачности 1.55 мкм.).
2. Формирование группового сигнала (из канальных сигналов).
Групповой сигнал формируется из элементов телефонных каналов (0.3 – 3.4 кГц).
Из анализа работы систем связи с частотным разделением каналов виден существенный недостаток:
сложность формирования группового сигнала.
Вопрос - формирование N-канального сигнала.
При серийном производстве LC-фильтров настройка каждого происходит индивидуально. В связи с внедрением цифровых фильтров проблема выделения боковых частот существенно упрощается.
В настоящее время используются трансмультиплексоры, которые являются сложными цифровыми фильтрами, работающими в реальном масштабе времени.
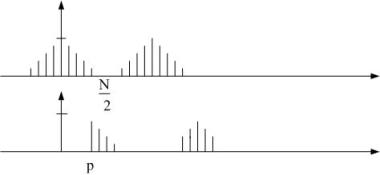
При формировании группового сигнала надо исходный спектр сигнала сдвинуть на p-тактовых интервалов в правую сторону.
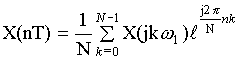
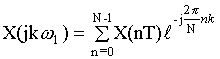
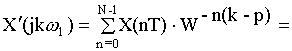
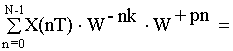
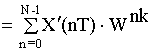
При сдвиге вправо на p-тактовых интервалов надо домножить исходный сигнал на две составляющие:
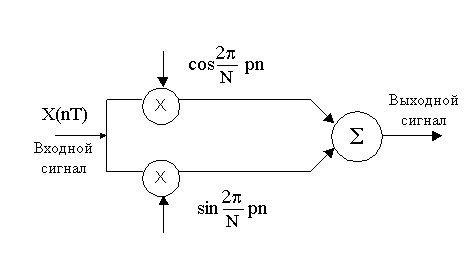
Данный алгоритм выигрывает по сравнению с известными аналоговыми способами формирования нижней и верхней области частот. Структура преобразования проще и легче перестраиваема. Вся перестройка в замене p.
Эта операция переноса спектра является умножением (разложением) сигнала на синфазную и квадратурную составляющую.
Литература:
Маркин С. “Цифровые сигнальные процессы”.
Цифровые сигнальные процессы.
Этапы развития можно разбить:
1. разработка сигнального процессора МПД 7720 (для синтеза устройств преобразования сигналов)
2. ТМS3301, ТМS 3302
3. ТМS 3303 за 2 мкс., АДSP-21.
Обработка сигналов для радиотелефонов осуществляется с помощью МП DSP.
DSP используется при синтезе так называемых модемов (устройств стыков между ПЭВМ и существующей сетью локальных или глобальных), DSP используется при синтезе трансмультиплексоров.
Сравнительная таблица различных типов DSP.
| возможности | 21.01 | 21.03 | 21.05 | 21.11 | 21.
MSP50 |
21.61
21.62 |
21.63
21.64 |
21.71
21.73 |
21.72 | 21.15 | 21.81 |
| Память
программ RAM |
2кБай-
та |
2к | 1к | 2к | 2к | - | - | 2к | 2к | 1к | 16к |
| память пр-м
неперест-мая ROM |
- | - | - | - | - | 8к | 4к | - | 8к | - | - |
| память дан-ных RAM | 1к | 1к | 0.5к | 1к | 1к | 0.5к | 0.5к | 2к | 2к | 0.5к | 16к |
| наличие
таймера |
+ | + | + | + | + | + | + | + | + | + | + |
| послед.порт “0”многокан. | + | + | - | + | + | + | + | + | + | + | + |
| посл.порт”1” | + | + | + | + | + | + | + | + | + | + | + |
| порт XOTин-терфейса | + | + | + | + | |||||||
| порт ПДП | + | ||||||||||
| режим низ-кого энерго-потребления | + | + | + | + | |||||||
| аналог. Ин-терфейс | + | ||||||||||
| макс. F,МГц | 20 | 10.24 | 13.82 | 20 | 20 | 18.67;
10.24 |
18.63;
10.24 |
18.67;
10.24 |
18.67 | 20 | 18.67 |
| длина цикла,
нс |
50 | 97.6 | 72.3 | 50 | 50 | 80;
97.6 |
80;
97.6 |
30;50 | 30 | 50 | 30 |
| Напряжение питания,В | 5 | 3.3 | 5 | 5 | 5 | 5;3.3 | 5;3.3 | 5;3.3 | 5 | 5 | 5 |
ПДП - прямой доступ к памяти – это режим в многопроцессорной системе, когда требуется из верхнего звена считать данные из более нижнего звена с отключением процессора низового звена.
Стык (согласование) с вышестоящим процессором, когда функции периферийного устройства выполняют выше названные.
В любом процессоре DSP три режима работы:
1. активный, работает на полную мощность;
2. режим приема команд скорость обработки сигналов уменьшается
3. режим молчания (при самом экономном энергопотреблении).
Из анализа совокупности характеристик наиболее перспективным является процессор 21 MSP 50 (ADSP-21-MSP-50) , наиболее быстродействующим является ADSP-2181.
Структурная схема сигнальных процессоров.
Стандартна для всех, отличие одной структуры от другой – в наличии или в отсутствии каких-то составных блоков. Для уменьшения времени выполнения в структуре предусмотрены два генератора в адресном пространстве DAG1 и DAG2 (аппаратный накопитель умножителей), позволяют за один такт умножить два 40-разрядных числа и прибавить полученное произведение к предыдущему результату.
Блок MAC – умножитель накопителей.
АЛУ – арифметическое логическое устройство, позволяет произвести сложение либо вычитание
логич.+, *, сложение по модулю 2.
Для обмена с внешними устройствами существуют специальные порты (SPORT) , у отдельных процессоров специальных портов несколько: последовательные “0”,”1” и последовательный XOT интерфейс.
В каждом из перечисленных выше процессоров имеется возможность организации памяти барабанного типа SHIFTER.
Устройство обмена позволяет переслать данные с одной шины на другую (с шины DMD на PMD и наоборот), согласовывать разный формат данных (PMD (24 разряда) и DMD (16 разрядов)).
Процессор в отличие от существующих процессоров имеет 5 шин:
Шина DMD-datamemorydata, вводятся исходные данные или окончательные результаты.
Шина PMD – шина инструкций programmemorydata, может использоваться и для данных, подлежащих вычислению (для повышения производительности).
Шина адресов PMA – programmemoryaddress, при начальной загрузке процессора, а также при чтении рабочей программы из памяти программ RAM.
DMA – datamemoryaddress, предназначена для чтения памяти данных ROM, для организации обмена по последовательному интерфейсу через SPORT0 и SPORT1.
Согласно рекомендации МККТТ последовательный обмен производится с помощью телеграфного 5р.кода, может вводиться асинхронно.
ALU совместно с аппаратным умножителем МАG и АЗУ барабанного типа SHIFTER образует 5 шину: шину R, позволяет переслать промежуточные результаты вычислений или из ALU в MAG или наоборот; либо с задействованием SHIFTER, при этом операции происходят бок о бок. Для построения иерархической системы связи, когда DSP связь осуществляется через HOST интерфейс (является устройством, кроме HOST интерфейса имеет возможность связаться с шиной адреса через два мультиплексора).
В HOST интерфейсе используется параллельная RG защелка. Такая защелка позволяет синхронизировать информацию.
Надо предусмотреть стандартное устройство ввода /вывода.
ADSP
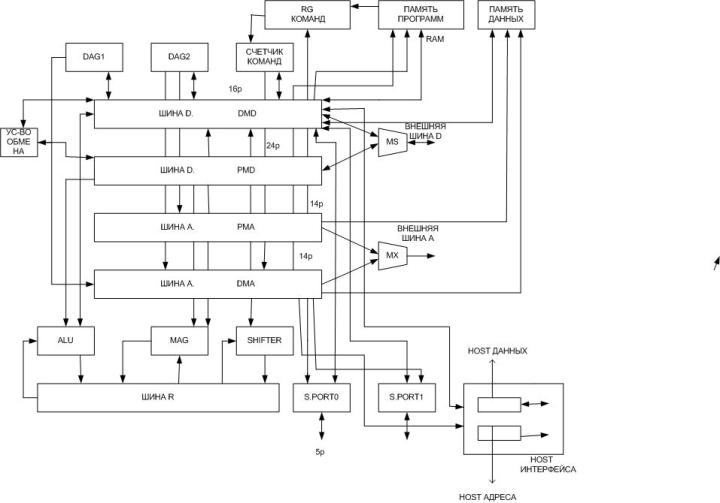
Сигнал Reset поступает программно от старшей по иерархии программной сетки. RG команд и счетчик обнуляются и указывают на нулевую ячейку памяти программ, где указан номер строки, с которой начинается первоначальная загрузка.
Установка всех составных блоков в исходное состояние.
Для того, чтобы разделить поток данных и поток инструкций (команд), используются 4 шины. Сигналы с одной шины в процессе обработки могут пересылаться на другую шину по специальной команде. Процесс разделения шин позволил существенно увеличить скорость обработки, для этой операции служат генераторы DAG1 и DAG2. Адресация в ОЗУ возможна в двух вариантах:
1. абсолютная адресация
2. косвенная адресация
Для уменьшения времени на выполняемую команду DAG1 и DAG2 автоматически инициируется.
Структура построения микропроцессорного комплекса.
Как и любая вычислительная система, сигнал. М.П.комплекс содержит три составляющие:
1. центральный процессорный элемент
2. постоянное запоминающее устройство первоначальной инициализации и хранения памяти программ
3. операторное запоминающее устройство
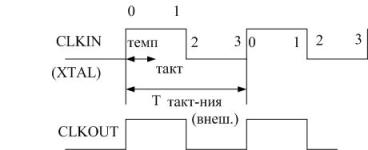
CLKIN и XTAL предназначены для подключения внешнего кварцевого резонатора, либо для подключения внешней тактовой частоты.
В случае, если используется внешняя тактовая частота, то тактовые импульсы подаются CLKIN, а вход XTAL остается свободным. Внутри центрального процессорного элемента происходит умножение тактовой частоты на 4. Совместно с тактовой частотой производится синхронизированный вывод выполняемых операций на выходе CLKOUT.
Вход RESET – вход сброса аппаратной реализации, по этому входу МПК сбрасывается в исходное состояние при первоначальном включении.
Вход MMAP – memory map control signal.
MMAP – вход для программного сброса, происходит обнуление сигналов от более старшего МП комплекта.
SPORT1 и SPORT0 – два последовательных устройства ввода/вывода, которые позволяют производить не только обмен данных, но и делать прерывание, более старшие прерывания IRQ-0, следующие IRQ-4.
В отличие от известных управл.процессоров прерывание может производиться как с последующего устройства ввода/вывода, так и ADSP. В случае если процессор работает в многопроцессорной системе, то используется постпроцессор.
а) отладка рабочей программы, тогда вместо постпроцессора используется ЭВМ
б) используется многопроцессорная система - сигнал.процессор (ближнего и дальнего уровня)
Центральный процессорный элемент имеет три шины: ША(14р.), ШД(24р.), Ш Управления (включает три сигнала, разделенные во времени:
); определяет порядок работы внешней памяти.
Если 
0, то производится обращение памяти к первоначальной инициализации
Для того, чтобы прочесть в памяти данных, вырабатывается сигнал
, а записать –
.
При первоначальной инициализации ввод производится по 4 байта, при этом в начале первый байт.
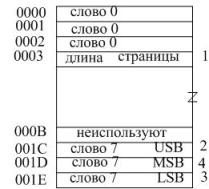
Структура АЛУ.
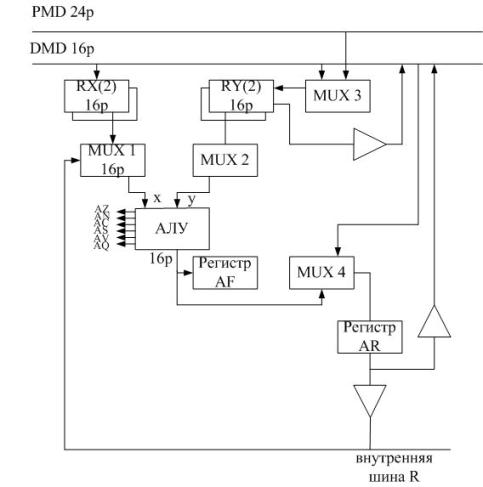
АЛУ – самостоятельный блок, входящий в процессор ATSP, позволяет выполнить:
1. R=x+y 9. R=x XQR y
2. R=x-y 10. R=PASS x
3. R=y-x 11. R=PASS y
4. R=x+y+CI 12. R=NOT x
5. R=x-y-CI+1 13. R=NOT y
6. R=y-x-CI+1 14. R=x+1
7. R=x OR y 15. R=y+1
8. R=x AND y
АЛУ состоит из блока RGx (2
16 раз.), блока RGy (2
16 раз.). Каждый из этих RG обрамлен мультиплексором, с его помощью сигнал может приниматься с двух направлений.
Первый блок RGRx совместно с мультиплексором MX1 позволяет выдать на вход сигнал либо с выхода Rx, либо с внутренней шины R.
MUX2 позволяет сделать аналогичные операции с выхода Ry и AR.
MU3 позволяет объединить шины DMD и PMD для записи второго операнда y, обе шины имеют разную разрядность (16 р. и 24 р.). Согласование разрядности происходит автоматически. Для выбора RGRy существуют два банка данных, для выбора нулевого банка данных надо указать команду MSTAX0.
При выполнении арифметических и логических операций формируются признаки:
1. AZ - признак нуля
2. AN- признак отрицательного результата
3. AC - признак переноса из 16 в 17 раз
4. AS - признак знака
5. AV - признак переполнения
6. AQ- признак частного
Структура умножителя MAC.
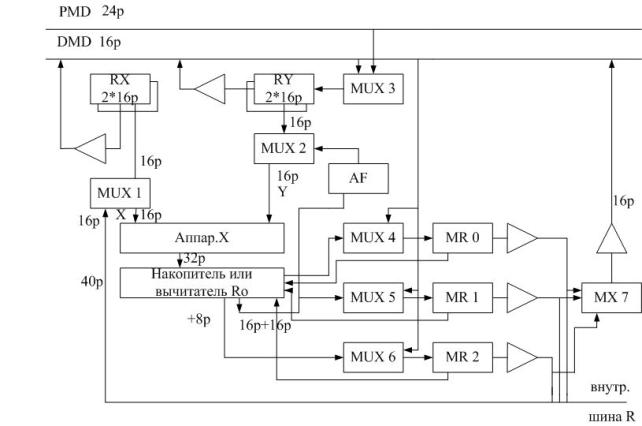
1. R=xy
2. R=MR+xy
3. R=MR-xy
4. MR=0
MAC состоит:
1. блок 2
16р. RG
для согласования 16р MR0 – MR1
MUX1 нужен для коммутации
MUX2
MUX3 коммутирует входные сигналы либо с шины DMD, либо с PMD.
MUX4-6 коммутирует на входы RGMR0-MR2, либо с выхода накопителя (вычитателя) R0-R2, либо с шины DMD. Специально ориентирован на временные свертки.
Два банка Rx и Ry постоянно меняются местами при вычислении свертки.
Список литературы
1. Гоноровский «Радиотехнические цепи и сигналы».
2. Голденберг Справочник по ЦОС.
3. Карташов «Основы теории дискретных сигналов и цифровых фильтров».
4. Робинер «Теория и применение ЦОС».
5. Ленг «Аналоговые и цифровые фильтры».
6. Антонию «Цифровые фильтры, анализ и проектирование».