Дальнейшим развитием оптимального статистического кодирования является кодирование кодовых слов. В этом методе применяется также оптимальное кодирование по методу ШеннонаФаноХаффмена, однако не к отдельным буквам, а к кодовым словам (сочетаниям n букв первичного сообщения). Статистическое кодирование слов позволяет ещё больше уменьшить среднюю длительность сообщений, так как алфавит источника быстро увеличивается с увеличением длины слова. Число возможных кодовых слов (алфавит источника после объединения букв) определяется выражением m=kn, где k - алфавит букв первичного сообщения. Пусть, например, у нас имеется двоичный источник, дающий буквы а1 и а2 (например, “1” и “0”). При передаче этих букв по каналу связи используются сигналы длительностью tэ, а .

Рассмотрим пример, когда p(а1)=0,8 и p(а2)=0,2 (если вероятности p(а1) и p(а2) равны между собой, никакое кодирование не может уменьшить среднюю длительность сообщения). Образуем из элементов а1 и а2 слова из двух букв(n=2), беря различные сочетания из этих букв. Если у нас источник с независимым выбором элементов сообщений, то

p(а1а1)=0,8×0,8=0,64;

p(а1а2)= p(а2а1)=0,8×0,2=0,16;

p(а2а2)=0,2×0,2=0,04.

Применяя к полученным словам кодирование по методу ШеннонаФано, получаем кодовое дерево (рис. 7), из которого видно, что новые комбинации неравномерного кода имеют длительность tэ, 2tэ и 3tэ.

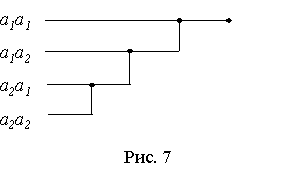
Средняя длина кодового слова

.

Но так как каждое слово содержит информацию о двух буквах первичного сообщения, то в расчёте на 1 букву получаем . Отсюда видно, что средняя длина элемента сообщения сократилась по сравнению с первоначальной в 1/0,78=1,38 раза.

Если усложнить кодирование и использовать n=3, то в этом случае получим . Это – уже почти предел, дальше уменьшать уже нецелесообразно. Чтобы убедиться в этом, рассчитаем производительность источника сообщений для всех трёх случаев.

Энтропия источника

.

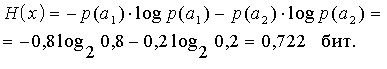При отсутствии статистического кодирования ,

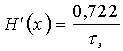бит/с.

При кодировании слов по две буквы ,

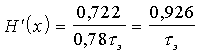бит/с.

При кодировании по две буквы

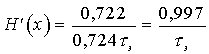бит/с.

Последняя величина близка к предельно возможной величине 1/tэ.

Статистическое кодирование слов целесообразно применять также в случае использования эргодического дискретного источника (источника с корреляционными связями букв), так как объединение букв в слова приводит к разрушению корреляционных связей (величина n должна быть не менее порядка эргодического источника, а n×tэ , соответственно, больше интервала корреляции букв первичного сообщения). Корреляционные связи между буквами трансформируются в различные вероятности появления возможных слов (n - буквенных сочетаний).

При этом необходимо помнить, что вероятность nбуквенных сочетаний определяется не произведением вероятностей отдельных букв, а, в соответствии с теоремой умножения, вероятностей надо учитывать также условные вероятности. Так, например, для источника с независимым выбором букв p(a1a1)=p(a1)×p(a1), а для эргодического источника с корреляционными связями букв p(a1a1)=p(a1)×p(a1/a1).

Вопросы

1. Какая цель достигается объединением букв в слова при оптимальном кодировании источников независимых сообщений?
2. Что является математической моделью источников сообщений с корреляционными связями?
3. Какая цель достигается объединением букв в слова при оптимальном кодировании источников зависимых сообщений, как выбирается длина кодовых слов?
4. Как осуществляется оптимальное кодирование сообщений с корреляционными связями?
5. В чём отличия алгоритмов оптимального кодирования кодовых слов для источников независимых и зависимых сообщений?