3.1. Метод последовательного функционального анализа

3.2. Метод половинного разбиения

3.3. Метод «время-вероятность»

3.4. Метод на основе информационного критерия

3.5. Инженерный метод

3.6. Метод на основе иерархического принципа

3.7. Метод ветвей и границ

3.8. Метод диагностики на основе «белого шума»

3.9. Метод диагностики на основе ортогонального анализа отклика системы по базису гармонических функций

Выбор того или иного метода использования информации о техническом состоянии диагностируемой аппаратуры обусловлен структурой ОД и требуемой глубиной поиска неисправностей. Он накладывает определенные требования на принципы построения и структуру системы контроля и диагностики.

Вид алгоритма (программы) поиска неисправностей существенно влияет на эффективность процесса контроля и диагностики. При разработке алгоритма поиска обычно решают две задачи:

а) определяют наилучший набор контролируемых параметров;

б) получают наилучшую последовательность измерения контролируемых параметров;

Рассмотрим наиболее распространенные методы построения алгоритмов поиска неисправностей в РЭА.

3.1. Метод последовательного функционального анализа

Построение алгоритма поиска неисправностей методом последовательного функционального анализа, заключается в последовательном измерении параметров схемы, начиная «с конца», то есть с выхода устройства, где либо вовсе отсутствует сигнал, либо он находится вне допуска, до тех пор, пока не появится на каком – либо блоке (узле, элементе) сигнал, находящийся в поле допуска. Такой поиск можно проводить и «с начала», с входа устройства. Основные функции, характеризующие исправность ОД, например:

а) электрического питания;

б) приема и преобразования сигналов заданной частоты;

в) управления;

г) генерирования колебаний.

Рассмотрим составление алгоритма поиска неисправностей на примере канала звукового сопровождения телевизора типа УПИМЦТ (Рис. 4). Основной функцией этого канала является усиление и преобразование сигналов звукового сопровождения. Эта функция выполняется, если при входном сигнале с фиксированными параметрами на выходе будет наблюдаться вполне определенный сигнал. В процессе контроля принимается решение об исправности или неисправности канала. Последовательно контролируя сигналы на выходе каждого каскада, можно определить неисправный каскад. Получающуюся при этом схему поиска называют деревом функций (Рис. 5), а решения представляют обычно в виде матрицы:

Табл. 3

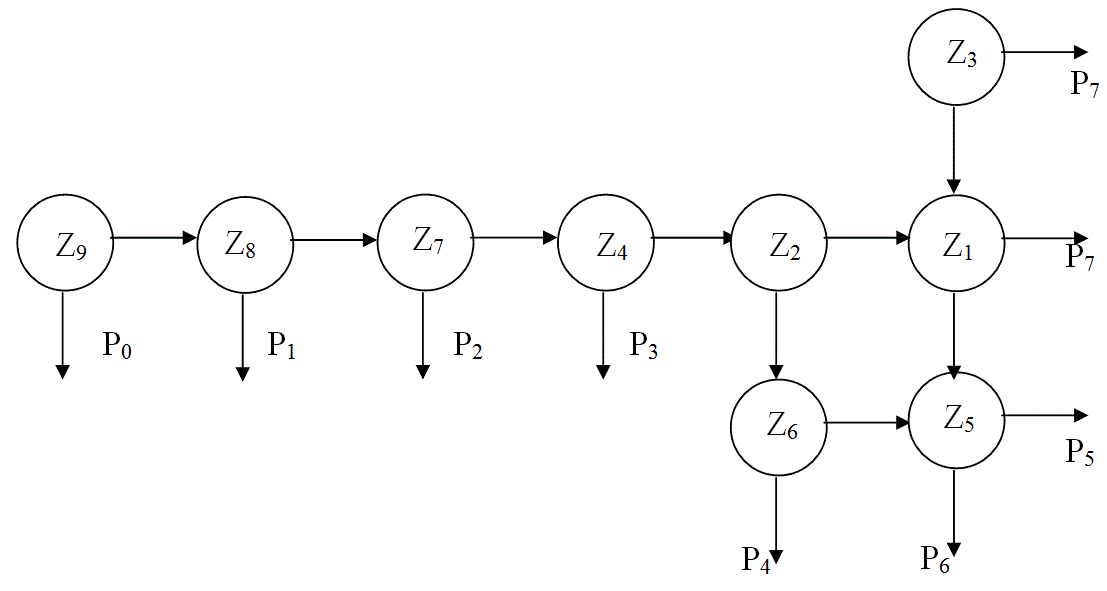
Рис. 5 Схема поиска неисправностей

Данный метод прост, нагляден, требует минимум информации от ОД, однако он не оптимален ни по времени, ни по средним затратам.

3.2. Метод половинного разбиения

Этот метод часто используется в разработке алгоритмов поиска неисправностей в РЭА с последовательно соединенными элементами. Первым для контроля выбирается параметр, делящий всю схему пополам. При положительном результате контроля (сигнал на выходе элемента находится в допуске) следующим для контроля выбирается элемент, делящий неисправную часть схемы пополам и так далее до определения неисправного элемента (блока, узла). Такой алгоритм возможен в том случае, когда вероятности состояний P(S_i) одинаковы для всех элементов, стоимости контроля выходных параметров Z_i также одинаковы.

В том случае, когда вероятности состояний P(S_i) для функциональных элементов неодинаковы, тогда вероятности необходимо первым контролировать такой параметр Z_k , который делит ОД на части, вероятности состояния которых близки к 0,5.

Неопределенность состояния ОД до контроля оценивается величиной энтропии

_N

H₀ = - ∑ P(S_i)*log₂ P(S_i) = log₂ N (13)

ⁱ⁼¹

Неопределенность состояния ОД при контроле параметра Z_k будет:

H(Z_k) = - (P_k *log₂ P_k + (1- P_k) *log₂ (1- P_k)) , (14)

_N

где P_k = ∑ P(S_i) , i = 1, 2, 3, …

ⁱ⁼¹

Величина H(Z_k) будет максимальна, если разность (P_k – 0,5) минимальна.

После контроля параметра (Z_k) ОД будет разделен на две части: первая содержит K, а вторая (N - K) элементов. При выборе очередного параметра для контроля необходимо вероятности состояний в каждой из этих частей пронормировать, пересчитать по формулам:

_k

P'(S_i) = P(S_i)/ ∑ P(S_i) , i = 1, 2, 3, … k (15)

^{i = 1}

_N

P" (S_i) = P(S_i)/ ∑ P(S_i) , i = k + 1, k + 2, … , N (16)

^i=k+1

При этом

_{k N}

∑ P' (S_i) = 1 и ∑ P" (S_i) = 1. (17)

^{i = 1 i=k+1}

Тогда вторым параметром выбирается Z_ll , который делит одну из частей на две, вероятности которых

_l

∑P" (S_i) = 0,5 (18)

ⁱ⁼¹

Такое деление продолжается до тех пор, пока состояние ОД не будет определено с заданной глубиной.

Метод половинного разбиения применим и для случая, когда в ОД неисправно несколько элементов.

3.3. Метод «время-вероятность»

Этот способ находит применение для РЭА, в которой функциональные элементы соединены произвольно и имеют разные вероятности P(S_i) состояний и различные стоимости проведения контроля параметров С(Z_i). Эффективность метода оценивается средним временем поиска неисправного элемента или средним временем контроля одного параметра. Последовательность контроля параметров устанавливается в порядке уменьшения величины:

P(S₁)/ t₁> P(S₂)/ t₂> …> P(S_N)/ t_N (19)

Располагая в порядке уменьшения величины P(S_i)/t_i , получим следующую последовательность для контроля параметров:

Z_N → … → Z_K → … → Z_M → … → Z_C

3.4. Метод на основе информационного критерия

Метод построения алгоритма поиска неисправностей на основе информационного критерия позволяет выбрать минимальное количество контролируемых параметров и определить последовательность их контроля.

Исходными данными являются функциональная модель и таблица неисправностей.

Предварительно ОД разделяются на N функциональных элементов, вероятности состояний, которых принимаем одинаковыми

P(S_i) = P(S₁) = P(S₂) = …= P(S_N) =1/N (20)

Неопределенность состояний ОД до контроля определяется оценивается величиной энтропии

H₀ = log₂ N (21)

Результат контроля к - го параметра ОД дает некоторое количество информации о его контроле:

I_K = H₀ - H_K (22)

где H_K - средняя условная энтропия ОД при условии контроля к - го параметра.

H_K = P(Z'_K) Н_Z'K + P(Z⁰_K) Н_Z0K (23)

P(Z'_K) = 1/N ; P(Z⁰_K) = (N – m)/N, (24)

где m – количество единиц в к - ой строке.

H_K = log₂ m + log₂ (N – m) (25)

Контроль к – го параметра дает следующее количество информации:

(26)

Последовательно вычисляем значения I_K (где к = 1, N) и по убыванию I_K определяем значимость параметра Z_K . Первым контролируется параметр Z_K , дающий максимальное количество информации.

После контроля первого параметра определяют количество информации, получаемое при контроле каждого n оставшегося параметра относительно состояния, характеризующегося энтропией Н_ZK . Условная энтропия

H(z_n/z_K) = P(z'_n/z'_K)*Hz'_n/z'_K + P(z⁰_n/z⁰_K)*Hz⁰_n/z⁰_K +

+P(z⁰_n/z'_K)*Hz⁰_n/z'_K + P(z'_n/z⁰_K)*Hz'_n/z⁰_K (27)

где P(z'_n/z'_K) = m₁/N – вероятность положительного решения при контроле параметра Z_n в случае положительного решения при контроле параметра Z_K; m₁ – количество единиц в n-ой строке таблицы состояний относительно m единиц в к-ой строке; m₂ – количество единиц в n-ой строке относительно (N – m) нулей к-ой строки.

(28)

(29)

(30)

Hz'_n/z'_K = log₂ m₁ ; (31)

Hz⁰_n/z'_K = log₂ (m - m₁ ) ; (32)

Hz'_n/z⁰_K = log₂ m₂ ; (33)

Hz⁰_n/z⁰_K = log₂ (N - m - m₂ ) ; (34)

I (z_n / z_K) = H_K – H(z_n / z_K) . (35)

Выражение для вычисления количества условной информации имеет вид:

(36)

По максимуму условной информации выбирается второй контролируемый параметр. По такой же схеме выбираются все остальные параметры.

После всех расчетов строим схему поиска неисправностей.

Пример 3.4.1

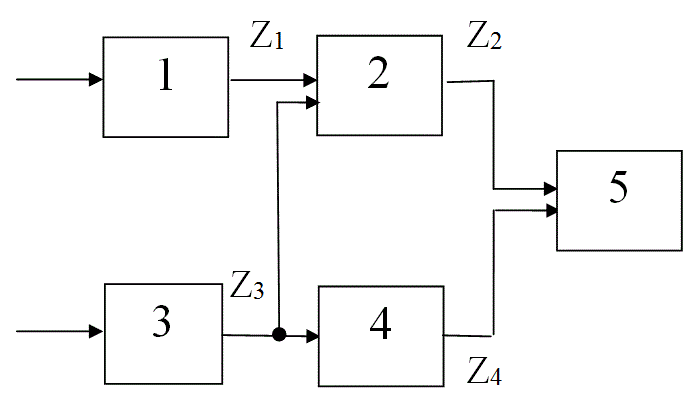
Рис. 6 Функциональная модель ОД

Табл. 4

Zi	Si
	S1	S2	S3	S4	S5
Z1	0	1	1	1	1
Z2	0	0	0	1	1
Z3	1	1	0	1	1
Z4	1	1	0	0	1
Z5	0	0	0	0	0

Из анализа табл. 4 находим, что контроль параметра Z₅ для поиска неисправностей не дает никакой информации, поэтому его можно из дальнейшего рассмотрения исключить. Тогда энтропия (21) до контроля будет

H₀ = log₂ 5 = 2,32

Количество информации (22) при контроле каждого параметра следующее:

I₁ =

I₂ =

I₃ =

I₄ =

Для контроля берем Z₂ . После его контроля могут быть приняты два решения: значение параметра Z₂ в допуске – функциональные элементы 1,2,3 исправны, а неисправность в элементе 4 или 5; (см. Рис. 6); значение параметра Z₂ не в допуске - функциональные элементы 4 и 5 исправны, а не исправность в элементах 1, 2, 3 .

В соответствии с этим решением перестраиваем матрицу состояний (табл. 5)

Табл. 5

Zi	Si
	S4	S5	S1	S2	S3
Z2	1	1	0	0	0
Z1	1	1	0	1	1
Z3	1	1	1	1	0
Z4	0	1	1	1	0

Теперь вычислим количество информации (36), которое дает контроль параметров Z₁ , Z₃ , Z₄ при условии, что Z₂ проконтролирован:

Следовательно, вторым для контроля выбираем Z₄ . Исключим из табл. 5 строку Z₂ (табл. 6)

Табл. 6

Zi	Si
	S4	S5	S1	S2	S3
Z4	0	1	1	1	0
Z1	1	1	0	1	1
Z3	1	1	1	1	0

В результате построения алгоритма поиска неисправностей в заданном ОД получаем, что для поиска неисправностей достаточно контролировать последовательность из трех параметров (Z₂ , Z₄ , Z₁) по определенной схеме (Рис. 7). Контроль параметра Z₄ при условии, что Z₂ = 1 дает два решения: если Z₄=0, то неисправен элемент 4, если Z₄=1, то неисправен элемент 5.

Если Z₂ = 0 и Z₄ = 0, то неисправен элемент 3 . Если Z₂ = 0 и Z₄ = 1, то надо контролировать параметр Z₁ . Если Z₁ = 0, то неисправен элемент 1, если Z₁ = 1, то неисправен элемент 2 (Табл. 7).

Табл. 7

Zi	Si
	S4	S5	S1
Z4	1	1	0
Z1	0	1	1
Z3	1	1	0

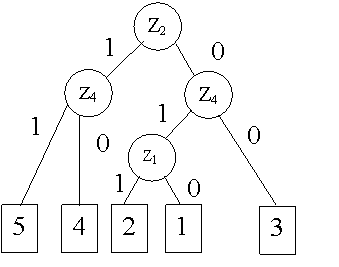
Рис.7 Схема поиска неисправностей

3.5. Инженерный метод

Этот метод построения алгоритмов диагностирования основан на вычислении функции предпочтения. При этом исходными данными являются функциональная модель ОД и таблица неисправностей.

Функция предпочтения выбирается в соответствии с решаемой задачей диагностики и исходными данными. При этом рассматриваются три случая определения перечня параметров:

а) для оценки работоспособности;

б) для поиска неисправностей;

в) для оценки работоспособности и поиска неисправностей.

Функция предпочтения при оценке работоспособности

N

W₁= max Wi (Z_i) = ∑ S₀ (i j) , (37)

^{i N j=1}

где S₀ (i j) = 1, если состояние i j–го матричного элемента описывается нулем, и S₀ (i j) = 0, если состояние i j–го матричного элемента описывается единицей.

Первым для контроля берут параметр Z_i, у которого функция W₁ (Z_i) имеет максимальное значение. В результате контроля данного параметра матрица состояний делится на две части. В одну часть входят состояния, для которых результаты контроля выбранного параметра имеют положительные, а в другую отрицательные решения. В дальнейшем надо контролировать только первую часть, так как нужно фиксировать только факт исправности или отказа. Для нее аналогичным образом нужно вычислить значения Wi (_Zi) и выбрать для контроля параметр по максимуму W_i (Z_i).

Пример 3.5.2

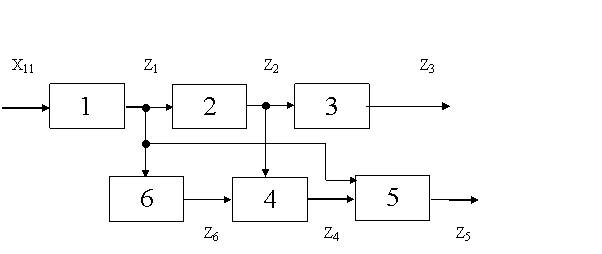
Рис. 8 Функциональная модель ОД

Табл. 8

Первым для контроля выбираем Z₅ по максимуму W₁ (Z₅). В результате контроля в строке Z₅ положительное решение имеет только Z₃ , следовательно следующим для контроля следует выбрать Z₃ .

Если для ОД известны вероятности состояний Р(S_i), то функция предпочтения

W₂ = max W₂ (Z_i) , (38)

^{i N}

_N

W₂ (Z_i) = ∑ P (S_i)S₀ (i j) , (39)

^{i =1}

Если для ОД известны и стоимости контроля параметров С(Z_i), то функция предпочтения

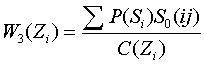(40)

Рассмотрим составление алгоритма поиска неисправностей. Максимальное количество информации дает контроль параметра, который делит все возможные состояния на две равные части. Тогда функция предпочтения

_{N N}

W₄ (Z_i) = min | ∑ S₀ (i j) - ∑ S₁ (i j)| (41)

^{j =1 j =1}

где S₁(i j) = 1, если состояние матричного элемента описывается единицей, и S₁ (i j) = 0, если состояние матричного элемента описывается нулем, S₀ (i j) = 1, если состояние матричного элемента описывается нулем, S₀ (i j) = 0, если состояние матричного элемента описывается единицей.

Первым для контроля выбирается параметр, для контроля которого функция предпочтения W₄ минимальна. Результаты контроля Z_i разделяют матрицу состояний на две части. В первую часть входят состояния, для которых результат контроля отрицателен (на пересечении Z_i – S_J стоит нуль), во вторую часть входят состояния, для которых результат контроля положителен. Для полученных частей вновь вычисляют функции предпочтения. По их минимальным значениям выбирают второй контролируемый параметр (при положительном исходе контроля первого выбранного параметра) или третий контролируемый параметр (при отрицательном результате контроля первого выбранного параметра). Совокупность параметров и последовательность их контроля выбирается до тех пор, пока множество N возможных состояний ОД не будет разделено на отдельные различимые состояния с требуемой глубиной поиска.

В случае, когда заданы вероятности состояний P(S_i) диагностируемой аппаратуры и стоимости контроля параметров С(Z_i) функциональных элементов, функции предпочтения примут вид

_{N N}

W₅ (Z_i) = min | ∑ P(S_i)S₀ (i j) - ∑ P(S_i)S₁ (i j)| (42)

^{j =1 j =1}

_{N N}

W₆ (Z_i) = min С(Z_i) | ∑ P(S_i)S₀ (i j) - ∑ P(S_i)S₁ (i j)| (43)

^{j =1 j =1}

Пример 3.5.3

Рис. 9 Функциональная модель ОД

Табл. 9

Для каждого параметра Z_i табл. 9 по формуле (41) определяется значение W₄ . Полученные значения записывают в табл. 10 и по минимальному значению выбирают для контроля параметр Z₃ .

Табл. 10

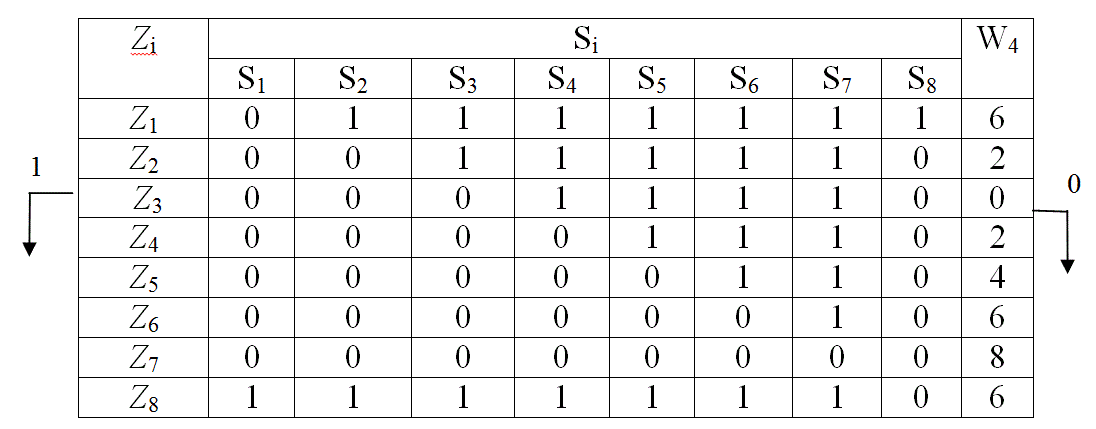
В результате контроля параметра Z₃ табл. 10 делится на две части: в первую часть входят функциональные элементы 4, 5, 6 и 7, для которых результат контроля Z₃ положителен, в другую часть входят функциональные элементы 1, 2, 3 и 8, для которых результат контроля отрицателен, что означает неисправность одного из этих элементов. При поиске неисправностей контролю подлежат обе части матрицы, поэтому каждую часть из них представляем в виде табл. 11, а другую табл. 12. Для каждой из полученных таблиц определяем значения функций предпочтения W₄. По минимуму W₄ в табл. 11 выбираем для контроля параметр Z₁ , в табл. 12 выбираем для контроля параметр Z₅ . Аналогичные деления показаны в табл. 13 – 15. Схема поиска неисправностей показана на рис. 10.

Табл. 11

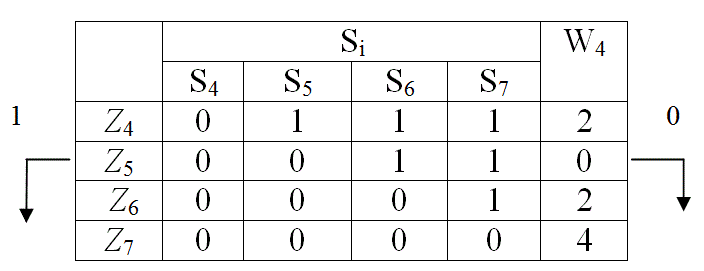
Табл. 12

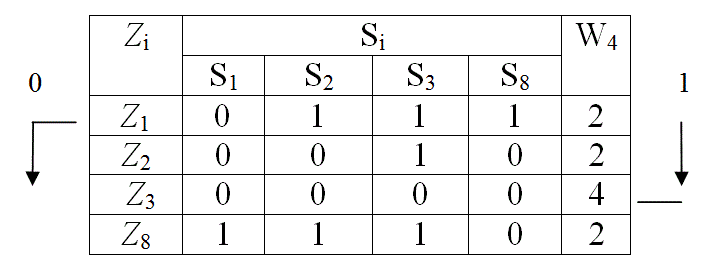
Табл. 13

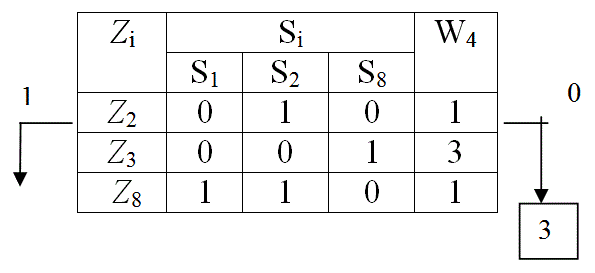
Табл. 14

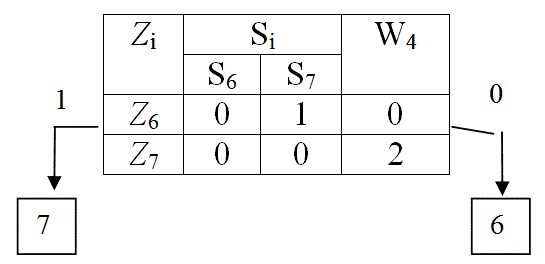
Табл. 15

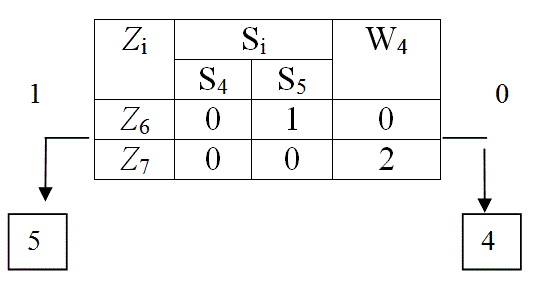
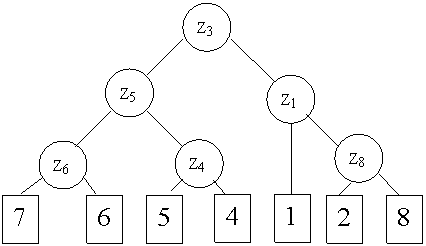
Рис. 10 Схема поиска неисправностей в диагностируемом устройстве

3.6. Метод на основе иерархического принципа

Построение алгоритмов диагностирования по иерархическому принципу целесообразно использовать для РЭА со встроенными устройствами контроля. При данном методе N первичных функциональных элементов ОД разбиваются к групп по N₁ элементов в каждой группе. Выходные параметры первичных функциональных элементов объединяются в одной точке с измерительным устройством и индикатором неисправности. Таких индикаторов будет к штук. Последние еще разбиваются на r групп по N₂ штук в каждой группе и т. д. В результате придем к одному индикатору неисправности.

В такой системе при выходе из строя функционального элемента последний индикатор покажет неисправность ОД. Для обнаружения неисправного функционального элемента просматриваются показания индикаторов первой ступени и при обнаружении индикатора, указывающего на неисправность, просматриваются индикаторы следующей ступени, соединенные только с этим индикатором. Проверки проверяются в указанной последовательности до тех пор, пока не будет обнаружен неисправный первичный элемент (рис. 11).

Поиск неисправного первичного функционального элемента по приведенной схеме позволяет значительно сократить время поиска по сравнению с поиском среди N элементов. Минимальное среднее время поиска неисправностей:

(44)

где

P(N) – вероятность пропуска неисправного элемента.

При и достигает максимума при z=4. Тогда количество ступеней иерархии

e = lnN /lnz (45)

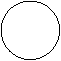
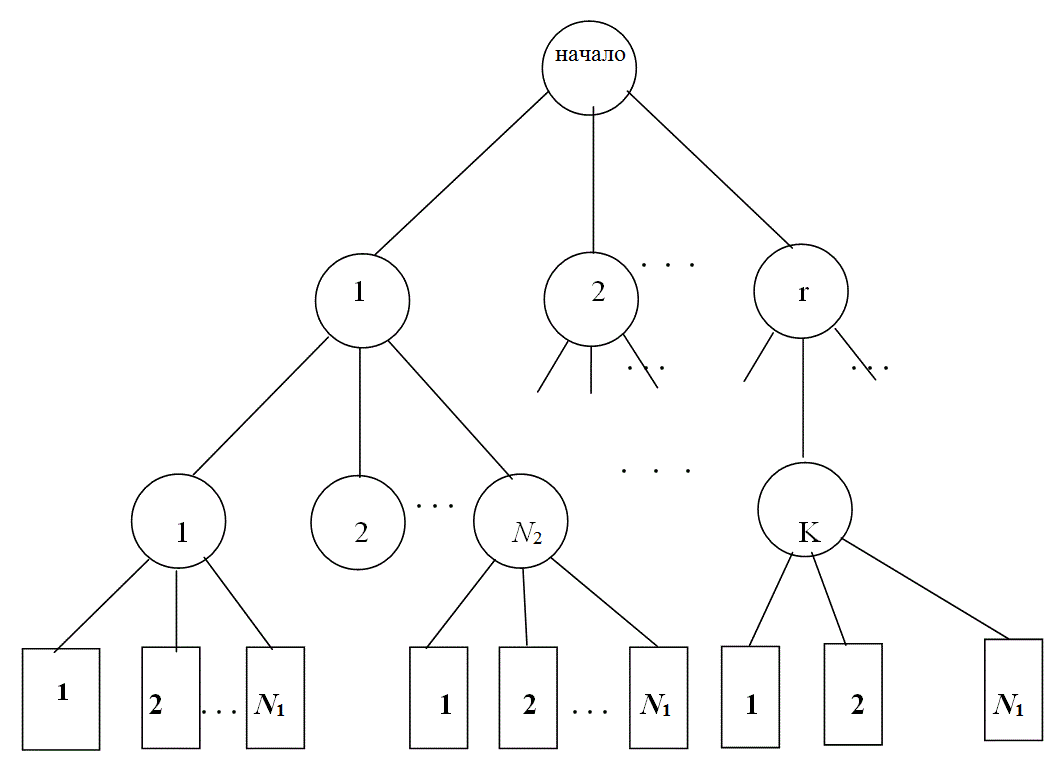
Рис. 11 Схема поиска неисправности по иерархическому принципу

3.7. Метод ветвей и границ

Способ построения алгоритма поиска неисправностей методом ветвей и границ используется для синтеза алгоритмов поиска неисправностей в РЭА, функциональная модель, которой представляет собой произвольную структуру. Он позволяет определить наилучшую последовательность поиска среди возможных. Исходными данными являются функциональная модель ОД, таблица неисправностей с вероятностями различных состояний и стоимости контроля выходных параметров функциональных элементов. Целью данного метода является определить такую последовательность контроля параметров, которая будет обладать минимальной средней стоимостью при поиске любого неисправного элемента.

Средняя стоимость произвольной программы поиска неисправностей

или , (46)

где C_i – стоимость контроля i – параметра;

- сумма вероятностей состояний, которые рассматриваются при контроле i – параметра.

Расчет поиска начинается с любого i – параметра, который разбивает всё множество возможных состояний S на два подмножества: S₀ (z_i) и S₁ (z_i), соответствующие отрицательному и положительному результатам контроля параметра z_i соответственно.

Последовательность контроля остальных параметров из приведенных подмножеств неизвестна, и определить значение средней стоимости алгоритма поиска невозможно. Поэтому значения средней стоимости заменяются их нижними границами С_н(S₀) и С_н(S₁) при контроле соответствующих параметров в подмножествах S₀(z_i) и S₁(z_i). Тогда нижняя граница средней стоимости всей программы поиска, которая начинается с контроля первого параметра, определяется как

(47)

Вычислив нижние границы стоимостей С_н(S₀) и С_н(S₁) для всех возможных алгоритмов поиска, выбирают первым такой параметр, контроль которого дает минимальную среднюю стоимость нижней границы алгоритма поиска.

Затем для подмножеств S₀(z_i) и S₁(z_i) вычисляют нижние границы стоимостей для всех возможных пар контролируемых параметров между первым и оставшимися для каждого подмножества.

Пусть для подмножества S₀(z_i) контролируется параметр z_к , а для подмножества S₁(z_i) – параметр z_j . Тогда нижняя граница средней стоимости программы поиска, начинающейся с контроля i – параметра, будет:

(48)

В общем виде записывается:

(49)

где (50)

(51)

где и - суммы вероятностей в подмножествах и соответственно.

Значения рассчитываются по формулам (46-48) для подмножеств

- подмножество состояний ОД, образующееся при отрицательном результате контроля параметров Z_iи Z_к;

- подмножество состояний ОД, образующееся при отрицательном результате контроля параметра Z_iи положительном результате контроля параметра Z_к;

- подмножество состояний ОД, образующееся при положительном результате контроля параметра Z_к и отрицательном результате контроля параметра Z_i;

- подмножество состояний ОД, образующееся при положительном результате контроля параметром Z_к и Z_i;

Вторым выбирается такой параметр, при контроле которого обеспечивается минимальная средняя стоимость нижней границы из всех возможностей алгоритмов поиска.

Аналогичным образом выбирают третий параметр и последующие параметры, пока получаемые пи контроле подмножества будут содержать более двух состояний ОД.

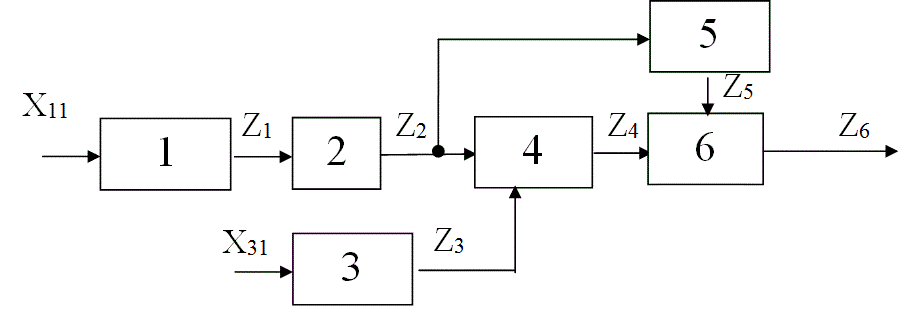
Рис. 12 Функциональная модель ОД

Матрица неисправностей и вероятности состояний

Таб.16

Пусть первым контролируется параметр Z₁. Тогда множество возможных состояний разбивается на два подмножества S₀(Z₁) и S₁(Z₁).Для подмножества S₀(Z₁) последовательность состояний вероятностей будет состоять из одного состояния Р(S₁) =0,2 , а подмножества S₁(Z₁) составим первую последовательность: Р(S₂) = 0,05; Р(S₅) =0,06; Р(S₄) =0,15; Р(S₃) =0,24; Р(S₆) =0,3. Затем определим сумму двух наименьших вероятностей: Р*₁ = 0,05 + 0,06 = 0,1.

Составим вторую последовательность: Р*₁ = 0,1; Р(S₄) = 0,15; Р(S₃) =0,24; Р(S₆) =0,03. Затем определим Р*₂ = 0,11 + 0,15 = 0,26.

Составим третью последовательность: Р(S₃) = 0,24; Р*₂ = 0,26; Р(S₆) =0,3. Затем определим Р*₃ = 0,24 + 0,26 = 0,5.

И наконец, составим четвертую последовательность: Р(S₆) =0,3; Р*₃ = 0,5 и определим Р*₄ = 0,3 + 0,5 = 0,8.

При этом нижняя граница средней стоимости

_{N 0 6-1-1}

С_н(Z₁) = С [ ∑ Р(S_i) + ∑ Р_λ + ∑ Р*_ν] = C (1 +0 +1,67) = 2,67 C

^{i=1 λ=1 ν=1}

Следует указать, что если подмножество S₀(Z_i) содержит одно состояние, то нижняя граница стоимости С_н(S₁) = 0.

Разделение множества возможных состояний на два подмножества S₀(Z₁) и S₁(Z₁) при контроле параметра Z₁ как показано в табл. 16.

При контроле параметра Z₂ множество возможных состояний разбивается на два подмножества: S₀(Z₂) и S₁(Z₂) (табл. 17).

Таб.17

Для подмножества S₀(Z₂) последовательность двух значений вероятностей будет из двух значений: Р(S₂) = 0,05 и Р(S₁) = 0,2 , и тогда Р*₁ = 0,05 + 0,2 = 0,25.

Для подмножества S₁(Z₂) первая последовательность будет иметь вид Р(S₅) =0,06; Р(S₄) =0,15; Р(S₃) =0,24; Р(S₆) = 0,3 , и тогда Р*₁ = 0,21; Р*₂ = 0,45; Р*₃ = 0,75.

Следовательно, нижняя граница средней стоимости при контроле параметра

_{N 0 6-1-1}

С_н(Z₂) = С [ ∑ Р(S_i) + ∑ Р_λ + ∑ Р*_ν] = C (1 +0,25 +1,41) = 2,66 C.

^{i=1 λ=1 ν=1}

Поступая аналогичным образом при контроле параметров z₃ , z₄ и z₅ , получим нижние границы стоимости при контроле соответствующих параметров: С_Н ( z₃ ) = 2,59C; С_Н (z₄) = 2,60С; С_Н (z₅) = 2,50С.

Из результатов вычислений нижних границ средней стоимости следует, что минимальной стоимостью будет обладать алгоритм поиска, начинающийся с контроля параметра z₅.

Посмотрим матрицу (табл. 18) состояний подмножества:

S₀ (z₅) и S₁ (z₅).

Анализируя табл. 18 , видим, что в случае отрицательного исхода при контроле параметра z₅ следующими можно контролировать параметры z₁ , z₂ , z₅. Параметр z₃ контролировать не имеет смысла, так как подмножество S₀(z₅) не разбивает при его контроле на более мелкие подмножества. При положительном исходе можно контролировать параметры z₃ , z₄.

Таким образом, необходимо вычислить значения стоимостей нижних границ алгоритма поиска при контроле таких наборов параметров z₅ , z₁ , z₃ , z₅ , z₁ , z₅ , z₂ , z₃ , z_{5 ,} z₂ , z₄. Для этого воспользуемся формулой:

,

где

;

Таблица 18

S1	ZI					P(S1)
	Z5	Z1	Z2	Z3	Z4
S1 0 0 0 1 0 0,2 S2 0 1 0 1 0 0,05 S3 0 1 1 1 1 0,06 S4 1 1 1 0 0 0,24 S5 1 1 1 1 0 0,15 S6 1 1 1 1 1 0,3

,

где ∑ Р(S_K) и ∑ Р(S_J) суммы вероятностей Р(S) диагностируемого объекта, которые различаются контролем параметров z_K и z_J в подмножествах и соответственно.

Вычислим значения стоимостей нижних границ при контроле параметров z₅ , z₁ , z₃ . Контроль параметров z₁ позволяет различать состояния S₁ , S₂ , S₅ , следовательно,

∑ P(S_K) = Р(S₁) + Р(S₂) + Р(S₂) = 0,2 + 0,05 + 0,06 = 0,31

Также при контроле параметра z_I выделяется из подмножества S₀(z_К) только одно состояние S⁰⁰₁ , тогда C_Н (S⁰⁰₁) = 0 , а значения C_Н (S₁⁰¹) вычисляется аналогичным способом , как и C_Н (S⁰₁) :

_К

C_Н (S₁⁰¹) = С ∑Р*_V = С [Р (S₂) + Р (S₅)] = C (0,05 + 0,06) = 0,11C

При контроле параметра z₃ различаются состояния S₃ , S₄ , S₆ , следовательно:

∑ P(S_J) = Р(S₃) + Р(S₄) + Р(S₆) = 0,24 + 0,15 + 0,3 = 0,69

Кроме того, при отрицательном исходе из множеств S₁(z₅) выделяется только одно состояние, а при положительном – два , следовательно:

C_Н (S¹⁰_J) = C_Н (S¹⁰₃) = 0

_К

C_Н (S¹¹_J) = С ∑ Р*_V = С [Р (S₄) + Р (S₆)] = C (0,15 + 0,3) = 0,45C

^V

Тогда значение стоимости нижней границы при контроле параметров z₅ , z₁ , z₃ будет равно

C_Н (z₅ , z₁ , z₃,) = С(1 + 0,31 + 0,11 + 0,69 + 0,45) = 2,56С

При контроле других последовательностей параметров вычисления осуществляются аналогично. Приведем результаты этих вычислений:

C_Н (z₅ , z₁ , z₄,) = 2,5С

C_Н (z₅ , z₂ , z₄,) = 2,64С

C_Н (z₅ , z₂ , z₃,) = 2,7С

Анализ результатов вычислений стоимостей нижних границ показывает, что минимальной стоимостью будет обладать последовательность параметров z₅ , z₁ , z_4.

Таблица19

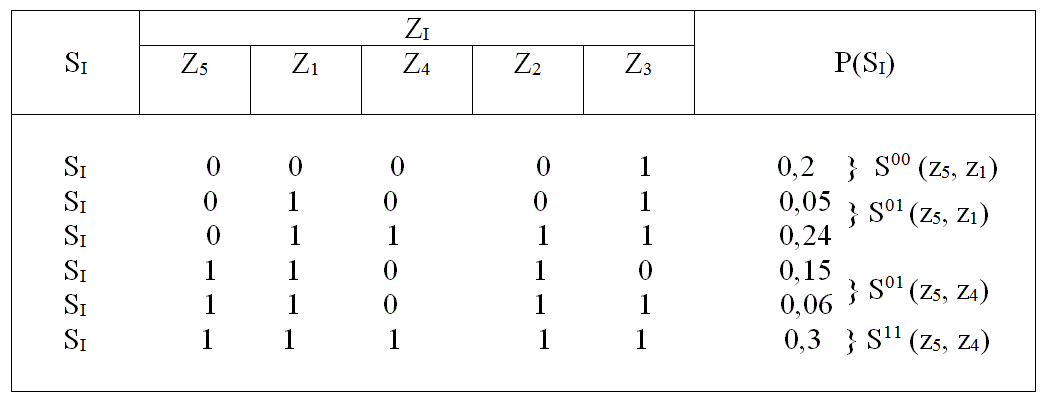
Преобразуем таблицу неисправностей в соответствии с результатами контроля последовательности параметров z₅ , z₁ , z₄ (табл. 19) .

Из таблицы видно, что при отрицательном исходе контроля параметров z₅ и z₁ выделяется состояние S₁ , а при отрицательном исходе контроля z₅ и положительном z₁ необходимо следующим контролировать параметр z₂ (контроль параметра z₃ не позволяет разделить подмножество S⁰¹ на более мелкие).

При положительном исходе контроля параметров z₅ и z₄ выделяется состояние S₆ , а при отрицательном исходе контроля параметров z₅ и отрицательном z₄ необходимо контролировать параметр z₃. Поскольку других вариантов нет, на этом заканчивается построение алгоритма поиска неисправностей, обладающего минимальной средней стоимостью (Рис. 13).

Таким образом, последовательность контролируемых параметров z₅ , z₁, z₄, z₂ , z₃ дает среднюю стоимость С_СР = 2,5С.

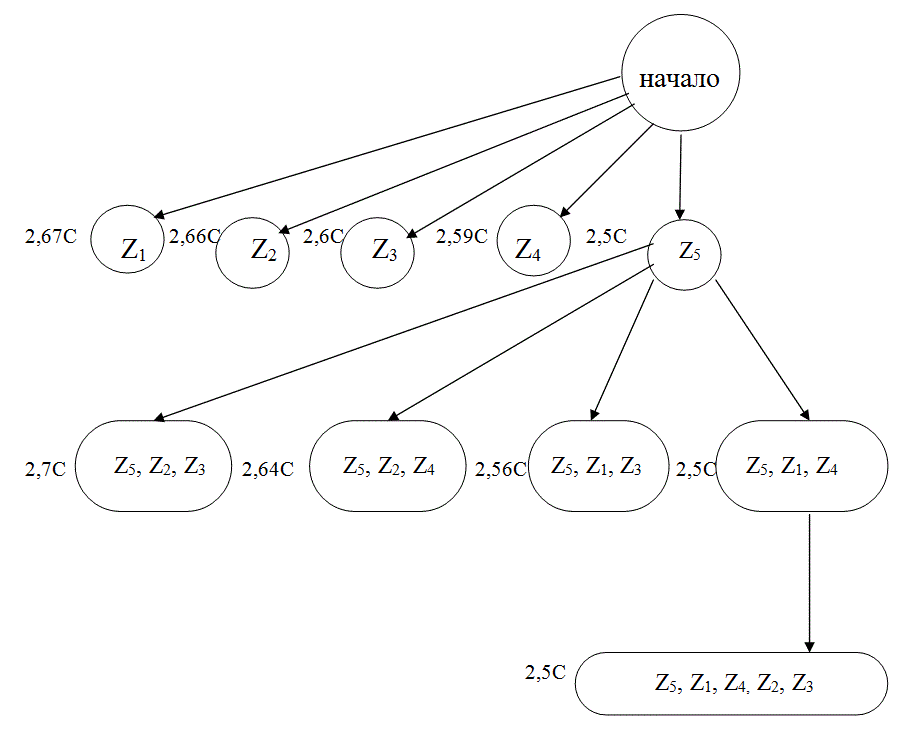
Рис. 13 Схема алгоритма поиска неисправностей, построенного методом ветвей и границ

3.8. Метод диагностики на основе «белого шума»

Интегральный метод диагностики на основе «белого шума» позволяет определить отклик диагностируемой системы во время ее нормальной работы, то есть без отключения. Известно, что для «белого шума» автокорреляционная функция равна нулю при всех значениях τ, кроме точки τ = 0, где случайная функция умножается сама на себя:

(51)

где U_ш1 (t) – напряжение белого шума на входе ОД.

Связь между напряжениями входа и выхода диагностируемой системы через отклик h(t) определяется уравнением

(52)

Известно, что взаимная корреляционная функция входа и выхода системы выражается через автокорреляционную функцию

(53)

После перемены аргументов τ и t получим

(54)

Если на вход системы подать стимулирующее напряжение

δ(t) = U₁(t) (55)

то уравнение (52) упрощается и напряжение на выходе системы становится равным отклику диагностируемой аппаратуры:

U₂ (t) = h (t) (56)

Из сравнения выражений (52), (53) и (56) следует, что при подаче на вход ОД сигнала в виде «белого шума», корреляционная функция которого является дельта-функцией R₁₁(t) = δ(t), взаимно корреляционная функция входа и выхода будет равна отклику системы:

R₁₂(t) = h (t) (57)

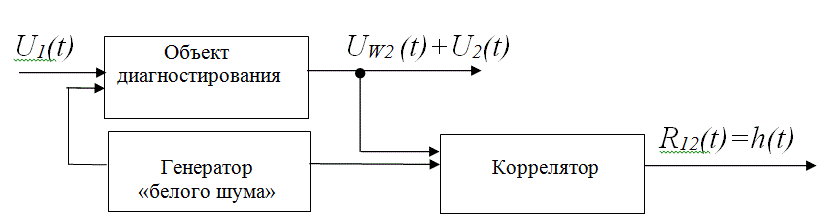
Рис. 14 Схема для определения отклика диагностируемой системы.

Равенство (7) позволяет синтезировать схему (рис.1), которая с помощью коррелятора может определить отклик системы по напряжению «белого шума» на ее входе.

Если на вход подать напряжение U_с1 (t), то на ее выходе получим суммарный сигнал

U₂ (t) = U_ш2 (t) + U_с2 (t) (58)

где U_с2 (t) – напряжение, которое появляется на выходе контролируемой аппаратуры после прохождения через нее сигнала U_с1 (t), U_ш2 (t) – напряжение на выходе аппаратуры.

3.9. Метод диагностики на основе ортогонального анализа отклика системы по базису гармонических функций

Известно, что динамические свойства любой радиотехнической системы можно описать её откликом h(t). Если отклик системы разложить в ряд Фурье и установить аналитическую связь между коэффициентами ряда Фурье для отклика и параметрами диагностируемой системы, то на этой основе можно проводить диагностирование. Отклик любой системы

< (59)

где М и С₀ – постоянные положительные действительные числа:

h(t) = 0 при t < 0 и h(t) 0 при t > 0.

Для отклика системы, удовлетворяющего условию (59) можно применить преобразование Лапласа:

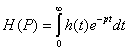
(60)

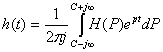
где функция h(t) является оригиналом, а функция Н(р) является изображением функции по Лапласу.

Учитывая условие (59) в формулах (60) можно положить С = 0 и р = jω.

Тогда получим преобразование Фурье:

(61)

Разложение функции h(t) в ряде Фурье в комплексной форме имеет вид:

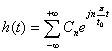(62)

где t₀ – для отклика h(t);

С_n – комплексные коэффициенты.

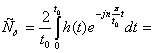
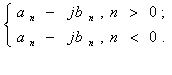(63)

Из сравнения (60) и (63) получаем формулы для определения коэффициентов Фурье:

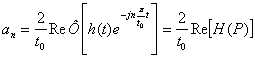, при (64)

, при (65)

Используя преобразование Лапласа, можно получить изображение выходного сигнала и передаточной функции.

S₂ (P) = S₁ (P)*K(p) (66)

Зная параметры элементов системы, можно вычислить её передаточную функцию К(р). Если параметры входного сигнала S₁(P) будут неизменными, то любые отклонения параметров системы за допустимые пределы будут отражаться в спектре выходного сигнала.

Связь между параметрами системы и коэффициентами ряда Фурье разложения передаточной функции можно продемонстрировать на примере.

Пример 3.9.5 Передаточная функция видеосигнала.

(67)

где {х} = К, Т₁, Т₂ – диагностируемые параметры (вторичные).

Решение. Определить вещественную и мнимую часть передаточной функции:

;

;

;

ω = n*ω₀ , где n – номер гармоники;

ω₀ – частота основной гармоники.

Для определения текущих значений диагностируемых параметров, составим систему уравнений, используя действительную часть передаточной функции:

;

(68)

.

Используя мнимую часть передаточной функции, получим другую систему уравнений:

;

(69)

.

В дальнейшем для упрощения вычислений используем относительные коэффициенты разложения:

В₁ = b₁/a₁ ; B₂ = b₂/a₂ ; …; B_n = b_n/a₂ . (70)

Используя текущие значения в относительных коэффициентов, составим систему уравнений:

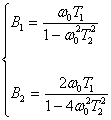(71)

Систему уравнений приведем к виду:

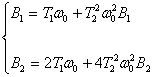(72)

Решая систему уравнений (71) и (72) относительно Т₁ и Т₂ , получим выражения для параметров диагностируемой системы:

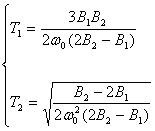(73)

Для определения коэффициента усиления К видеоусилителя воспользуемся уравнением:

. (74)

Отсюда:

. (75)

Полученные значения параметров сравниваются с их номинальными значениями. Параметр, вышедший из допуска, и определяет место неисправности.