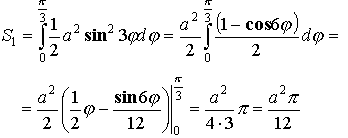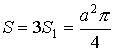3.1. Понятие первообразной и неопределенный интеграл
3.3. Основные методы интегрирования
3.1. Понятие первообразной и неопределенный интеграл
Основные определения
Функция 
называется первообразной для функции 
, если 
.
Т.1: Если 
и 
- первообразные для 
, то 
Доказательство:
; ЧТД.
Неопределенным интегралом от 
называется класс всех первообразных для 
.
- подынтегральная функция.
- дифференциал.
- переменная интегрирования.
Для любой непрерывной функции существует первообразная.
Основные тождества
1.
2.
3.
3.2. Таблица интегралов
1. 
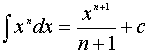
2. 
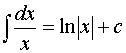
3. 
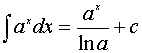
4. 
5. 
6. 
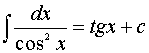
7. 
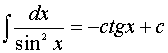
8. 
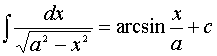
9. 
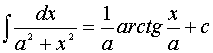
10. 
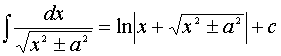
11. 
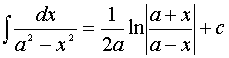
12. 
13. 
Доказательство каждого из табличных интегралов осуществляется с помощью дифференцирования (по определению). Например, для 10 и 11 табличных интегралов:
Доказательство:
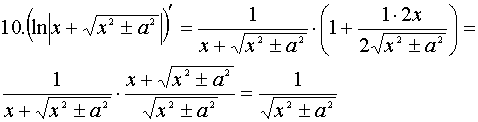
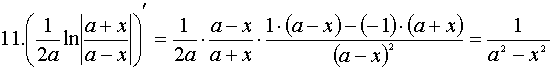
Основные свойства неопределенного интеграла
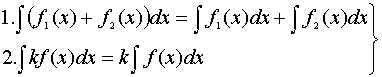- линейность
Следствие:
1.
; 
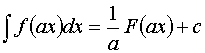
2.
3.3. Основные методы интегрирования
Замена переменных под знаком неопределенного интеграла
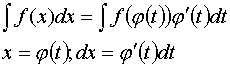
Интегрирование по частям.
Доказательство:
(формула дифференцирования произведения).
(интегрируем обе части равенства)
(использование основного тождества)
(что и требовалось доказать).
Пример:
1) (замена переменной)
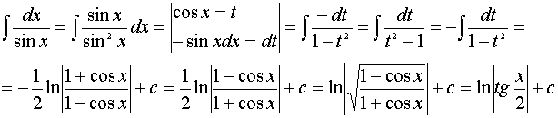
2) (интегрирование по частям)
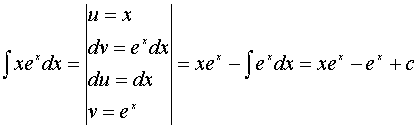
Дополнительный материал
Интегрирование рациональных дробей. Простейшие дроби и их интегрирование
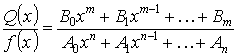
Все коэффициенты действительные числа.
m , n – целые числа.
Нет общих корней.
Если 
, то дробь называется неправильной, если 
, то дробь называется правильной.
Если дробь неправильная, то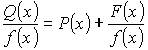 
, где 
- правильная дробь; 
- многочлен.
Простейшие дроби:
1.
2.
, 
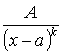и целое число.
3.
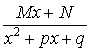( в знаменателе неприводимый квадратный трехчлен).
4.
, 
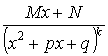и целое число.
=
=
=
=
=
=
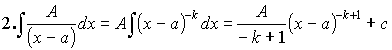
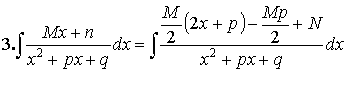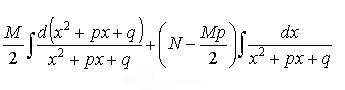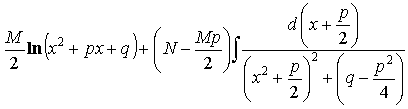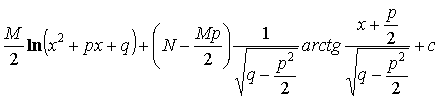
Разложить рациональные дроби на простейшие
Теорема. Если х = а – корень знаменателя f(x) кратности k , то
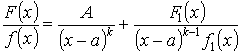
Доказательство:
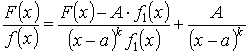; (1)
Будем подбирать А так, чтобы 
По теореме Безу это возможно, если
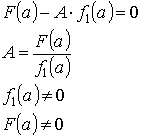
Тогда 
Подставим в (1)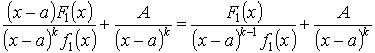 
Следствие:
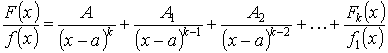
Теорема. Если 
(
- неприводимый квадратный трехчлен. 
), то
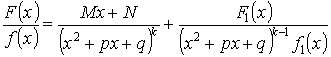
Доказательство:
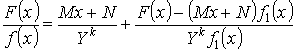
Подберем M и N так, чтобы числитель делился на Y :
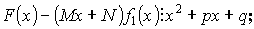
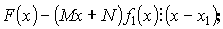
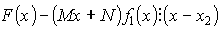
- по теореме Безу.
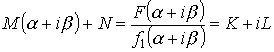
M и N можно найти из этой системы всегда.
Следствие: всякая правильная рациональная дробь может быть разложена в сумму простейших дробей.
Пример:
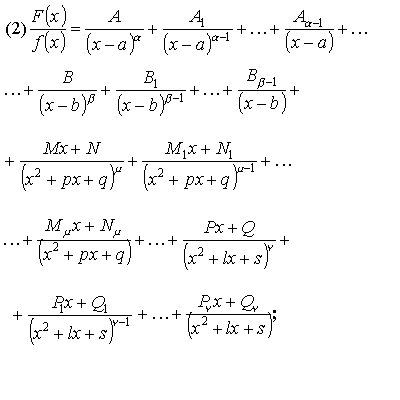
Метод неопределенных коэффициентов
Правую часть равенства (2) надо привести к общему знаменателю и приравнять в числители коэффициенты при одинаковых степенях F(x). Решая полученную систему уравнений можно определить все коэффициенты.
Интегрирование рациональных дробей
- Выделить целую часть дроби.
- Разложить знаменатель на множители.
- Представить в виде суммы простейших дробей.
- Найти неопределенные коэффициенты.
- Интегрировать каждую простейшую дробь.
Интегрирование иррациональных функций
3.3.1.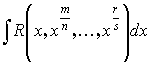 
k – общий знаменатель дробей 
- рационализирующая подстановка.
Пример:
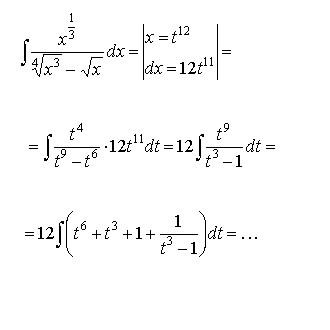
3.3.2.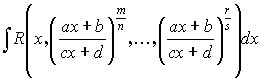 
k – общий знаменатель дробей
Пример:
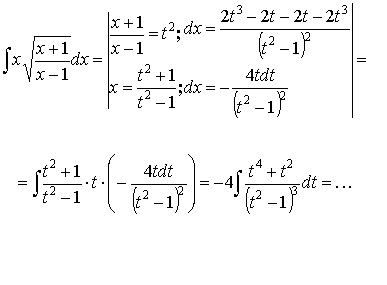
3.3.3. Тригонометрические подстановки.
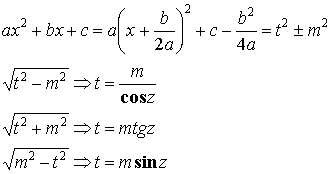
Пример:
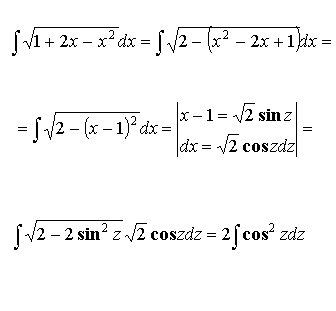
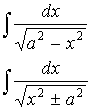- обратные гиперболические функции.
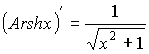
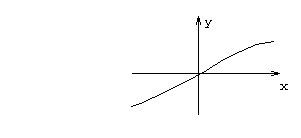
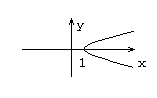
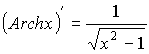
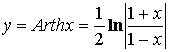
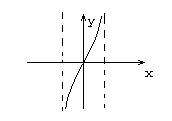
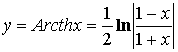
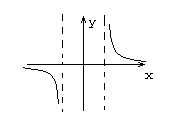
3.4. Понятие определенного интеграла и его вычисление
Определение и свойства
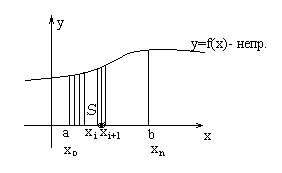
S – область – криволинейная трапеция.
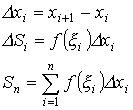
Интегральная сумма: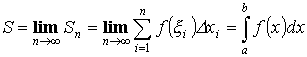
Определенным интегралом называется предел интегральной суммы.
Теорема. “О существовании определенного интеграла”
Если f(x) – непрерывна на отрезке (a,b), то определенный интеграл существует и не зависит от порядка разбиения и выбора точек.
Геометрический смысл определенного интеграла – площадь криволинейной трапеции.
Свойства определенного интеграла:
-
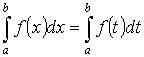
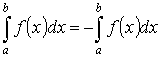
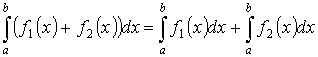
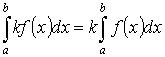
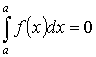
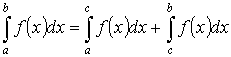- аддитивность.
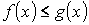на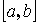 
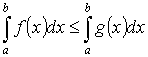
Основные теоремы интегрального исчисления
Теорема 1. “об оценке”
Пусть y =f(x) интегрируема на [a ,b] 
Тогда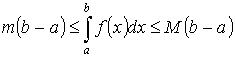 
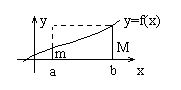
Доказательство:
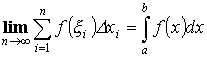
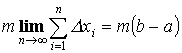
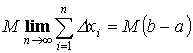
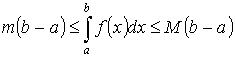
Теорема 2. “о среднем”
Пусть y =f(x) интегрируема на [a ,b] Тогда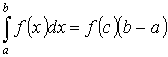 
- где 
f(c) – среднее значение f(x) на [a ,b].
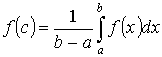
Доказательство:
По Т.1: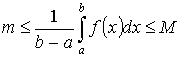
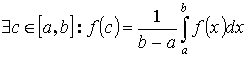
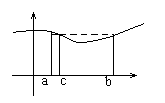
Т.к. f(x) – непрерывна на [a ,b], то она принимает все промежуточные значения от m до M. Следовательно она принимает значение
А. Т.е. существует такая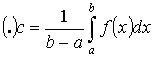 
Теорема 3. “о производной определенного интеграла по переменному верхнему пределу”
Пусть y =f(x) - интегрируема на [a , b]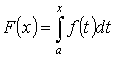
. Тогда 
Доказательство:
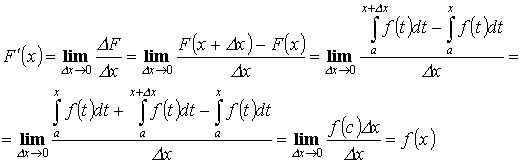
Теорема 4. “формула Ньютона-Лейбница”
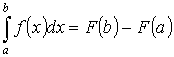, где F(x) – первообразная для f(x).
Доказательство:
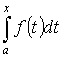- первообразная для f(x) по Т.3. Т.к. первообразные отличаются на const, то 
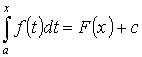Пусть х=а. F(a)+c=0. c=-F(x). Пусть x=b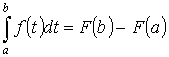 
Методы вычисления определенного интеграла
Замена переменных под знаком определенного интеграла.
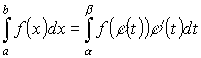
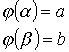
Пример:
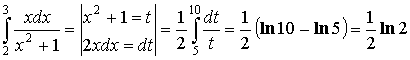
Интегрирование по частям в определенном интеграле.
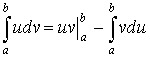
Пример:
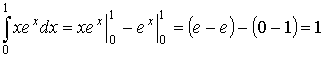
3.5. Приложения определенного интеграла
Площадь плоской фигуры (в декартовой системе координат)
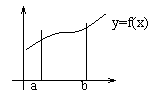
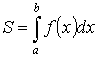- из определения
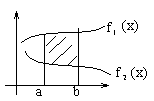
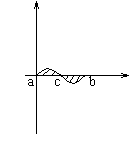
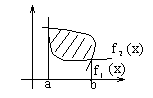
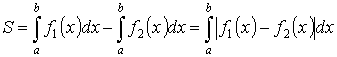
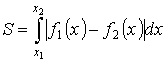
Площадь плоской фигуры (параметрическое задание)
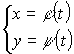
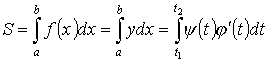
Пример:
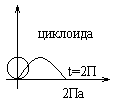
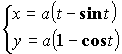
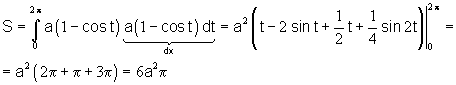
Площадь плоской фигуры (в полярной системе координат)
. 
. 
. 
.
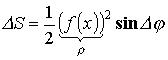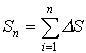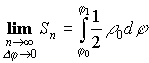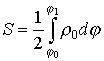Пример:
