Рассмотренный выше гармонический анализ периодических сигналов можно обобщить и на непериодические (одиночные) сигналы. Возвратимся к периодическому сигналу произвольной формы (рис. 2.6, а).

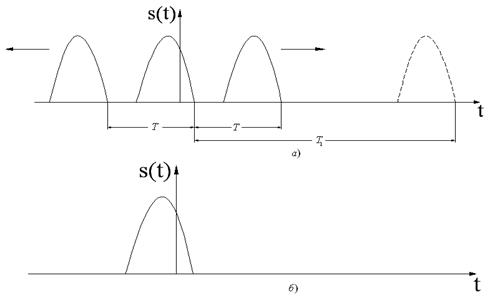
Рис. 2.6

Увеличим значение до . Соседние с центральным сигналы сдвинутся вправо и влево по оси времени. Если теперь устремить , на временной диаграмме (рис. 2.6, б) останется только одиночный сигнал конечной длительности. Если мощность сигнала отлична от нуля, то энергия такого сигнала конечна. Математически это условие равносильно требованию сходимости интеграла

,

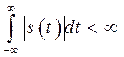где – абсолютное значение функции .

Иными словами функция должна быть абсолютно интегрируемой.

Обратимся к спектральным диаграммам (рис. 2.2, б, в). Т.к. расстояние по оси частот между соседними составляющими равно

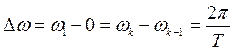, (2.24)

то с увеличением величина уменьшается и спектральные составляющие сближаются. При этом значения комплексных амплитуд составляющих уменьшаются. При величина и спектр из линейчатого становится сплошным и представляет собой бесконечно большое число гармоник и бесконечно малыми амплитудами.

Воспользуемся комплексной формой ряда Фурье (2.16). Подставляя в эту формулу выражение (2.17), получим

.

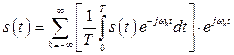Тогда с учетом того, что 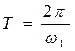и , запишем

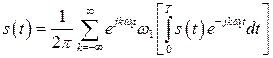. (2.25)

Т.к. в пределе при величина , то в соответствии с (2.24) превращается в бесконечно малое приращение , а частота k-той гармоники – в текущую частоту . При этом пределы внутреннего интеграла в (2.25) расширяются от до , а суммирование переходит в операцию интегрирования. С учетом этого выражение (2.25) принимает следующий вид:

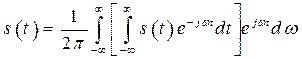. (2.26)

Интеграл, заключенный в скобки выражения (2.26), описывает комплексный спектр одиночного сигнала

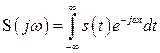. (2.27)

Тогда с учетом (2.27) выражение (2.26) запишется следующим образом

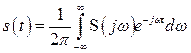. (2.28)

Выражения (2.27) и (2.28) представляют собой соответственно прямое и обратное преобразование Фурье.

Выясним физический смысл комплексного спектра одиночного сигнала. Зафиксируем некоторую частоту . Так как для периодического сигнала , то для вычисления комплексной амплитуды в выражении (2.17) пределы интегрирования можно распространить на область , т.е.

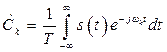. (2.29)

С другой стороны на этой же частоте для одиночного сигнала в соответствии с (2.27)

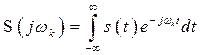. (2.30)

Так как интегралы в (2.29) и (2.30) совпадают, можно записать

, (2.31)

здесь период согласно (2.24) равен

,

где – элементарный интервал частот, измеряемый в герцах.

Тогда

.

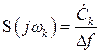В практической радиотехнике вместо комплексного спектра часто используют амплитудный спектр. В этом случае

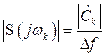. (2.32)

Отсюда следует, что характеризует плотность распределения амплитуд составляющих сплошного спектра одиночного сигнала по частоте. Если – изменяющиеся во времени напряжение или ток, то размерность составляет или .

Запишем (2.32) с учетом (2.24) в виде

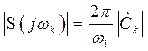. (2.33)

Отсюда следует, что огибающая сплошного спектра одиночного сигнала и огибающая соответствующего периодического сигнала совпадают по форме и отличаются только масштабом. На практике в ряде случаев при вычислении спектра периодического сигнала гораздо проще сначала найти одиночного сигнала, а затем, пользуясь соотношением (2.33) перейти к спектру периодического сигнала.

Преобразования Фурье (2.27) и (2.28) представлены в комплексной форме. Воспользовавшись известными соотношениями

, (2.34, а)

и

, (2.34,б)

можно получить тригонометрическую форму преобразований. Так, с учетом (2.34, б) выражение (2.27) принимает следующий вид

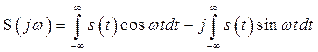, (2.35)

где первый интеграл представляет собой вещественную, а второй – мнимую часть , т.е.

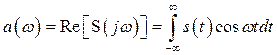, (2.36)

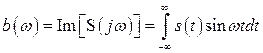. (2.37)

Тогда модуль или амплитудный спектр вычисляется по формуле

, (2.38)

а аргумент или фазовый спектр - в соответствии с выражением

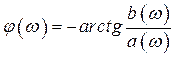. (2.39)

Если сигнал является четной функцией времени , то второй интеграл в (2.35) равен нулю, т.к. произведение является нечетной функцией, а пределы интегрирования симметричны относительно нуля. В этом случае описывается вещественной и четной функцией

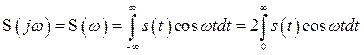. (2.40)

Если же сигнал является нечетной функцией времени, то первый интеграл обращается в ноль и представляет собой нечетную и чисто мнимую функцию частоты , т.е.

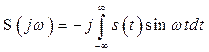. (2.41)

Таким образом (2.35), (2.40) и (2.41) характеризуют тригонометрическую форму прямого преобразования Фурье.

Обратимся теперь к обратному преобразованию Фурье (2.28).

С учетом того, что

,

выражение (2.28) можно представить в следующем виде

,

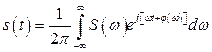или, в соответствии с (2.34,а)

.

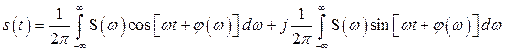Если – четная функция, то второй интеграл является нечетной функцией и его значение равно нулю. Тогда окончательно запишем

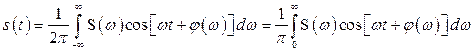. (2.42)

В качестве примера рассмотрим преобразование Фурье прямоугольного импульса длительности и амплитудой , определенного на интервале

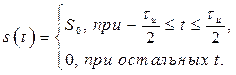
Воспользовавшись выражением (2.27), после несложных преобразований получим

.

На рис. 2.7 изображены форма импульса и его спектральная функция.

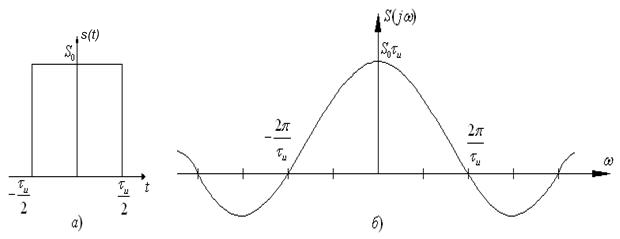
Рис. 2.7

Сравнение спектральных диаграмм рис. 2.4 и рис. 2.7,б показывает, что формы огибающей линейчатого и сплошного спектров совпадают, что подтверждает сделанные ранее выводы. При этом как огибающая линейчатого, так и огибающая сплошного спектров достигают нулевого значения на частотах ω = 2lπ/τ, где . При значение спектральной функции равно площади импульса.

Перейдем к рассмотрению основных свойств преобразования Фурье. Для краткости записи пару преобразований (прямое и обратное) символически будем представлять следующим образом:

1. Линейность преобразования Фурье

, (2.43)

где и – произвольные числовые коэффициенты.

Доказательство формулы (2.43) не вызывает затруднений, для этого достаточно подставить сумму в выражение (2.27).

2. Свойство временного сдвига (теорема запаздывания)

. (2.44)

Т.к. , то (2.44) можно представить в виде

. (2.45)

Таким образом задержка сигнала во времени на величину приводит к изменению его фазового спектра на .

3. Изменение масштаба времени

. (2.46)

В зависимости от величины имеет место либо сжатие , либо растяжение сигнала во времени. Из (2.46) следует, что при сжатии сигнала во времени в раз происходит расширение его спектра во столько же раз. И наоборот.

4. Операция дифференцирования

. 2.47)

При дифференцировании сигнала все гармонические составляющие его спектра изменяют начальную фазу на .

5. Операция интегрирования

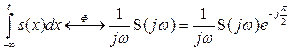. (2.48)

При интегрировании сигнала все гармонические составляющие его спектра изменяют начальную фазу на . Свойство (2.48) справедливо, если

.

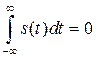6. Если , то

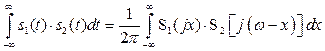. (2.49)

Интеграл в правой части выражения (2.49) называется сверткой. Таким образом, преобразование Фурье произведения сигналов представляет собой свертку (с коэффициентом ) их спектров. В частном случае при и равенстве двух сигналов можно получить следующее соотношение:

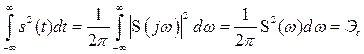, (2.50)

которое представляет собой интегральную форму равенства Парсеваля (2.22). Из этого соотношения следует, что полная энергия непериодического сигнала равна сумме энергий всех его спектральных составляющих. При этом зависимость

, (2.51)

представляет собой спектральную плотность энергии или энергетический спектр одиночного сигнала.