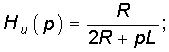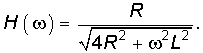7.1. Преобразование Лапласа и его свойства
7.3. Расчет переходных процессов операторным методом
7.1. Преобразование Лапласа и его свойства
Операторный метод берет начало со времени анализа бесконечно малых величин, когда были обнаружены определенные аналогии между дифференциально-интегральными и алгебраическими уравнениями. В XIX в. был опубликован ряд работ по операционному исчислению М.Е. Ващенко-Захарченко, О. Хэвисайда, Д. Карсона и др. Однако строгое обоснование операторный метод получил только в XX в. на базе общей теории функциональных преобразований.
В основе операторного метода расчета переходных процессов лежит преобразование Лапласа, которое позволяет перенести решение из области функций действительного переменного t в область комплексного переменного р:
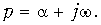
При этом операции дифференцирования и интегрирования функций времени заменяются соответствующими операциями умножения и деления функций комплексного переменного на оператор р, что существенно упрощает расчет, так как сводит систему дифференциальных уравнений к системе алгебраических. В операторном методе отпадает необходимость определения постоянных интегрирования. Этими обстоятельствами объясняется широкое применение этого метода на практике.
Различают прямое и обратное преобразование Лапласа. Прямое преобразование Лапласа определяется уравнением.
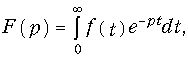
где f(t) — функция действительного переменного t, определенная при t 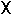 0 (при t < 0; f(t) = 0) и удовлетворяющая условиям ограниченного роста:
0 (при t < 0; f(t) = 0) и удовлетворяющая условиям ограниченного роста:
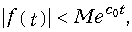
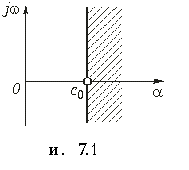
где множитель М и показатель роста с0 — положительные действительные числа. На рис. 7.1 изображена область определения функции комплексного переменного F(p).
Обратное преобразование Лапласа определяют из решения (7.2):
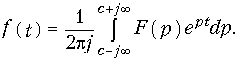
Функция F(p), определяемая уравнением (7.2), носит название изображения по Лапласу, а функция f(t) в (7.4) — оригинала. Следовательно, оригинал и изображение представляют собой пару функций действительного (t) и комплексного (p) переменного, связанных преобразованием Лапласа. Для сокращенной записи преобразований (7.2), (7.4) используют следующую символику
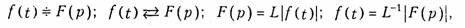
где L - оператор Лапласа. В дальнейшем для определенности будем использовать знак соответствия 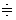 .
.
Рассмотрим основные свойства преобразований Лапласа.
Свойство линейности является следствием линейности преобразования Лапласа, его можно записать в форме
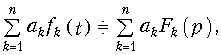
где ak — постоянные коэффициенты разложения. Свойство (7.5) легко доказать, если применить к левой части соотношения (7.5) прямое преобразование Лапласа (7.2).
Дифференцирование оригинала
При ненулевых начальных условиях: f(0–)¹ 0 дифференцирование оригинала соответствует следующему условию
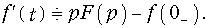
Для доказательства (7.6) подставим f¢(t) в преобразование (7.2) в виде
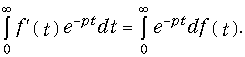
Отсюда после интегрирования по частям получаем:
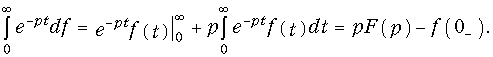
В случае нулевых начальных условий
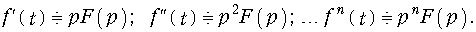
Интегрирование оригинала
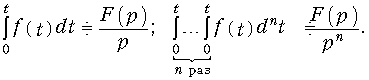
Доказательство осуществляется путем использования свойства дифференцирования оригинала (7.6), (7.7).
Изменение масштаба независимого переменного (теорема подобия)
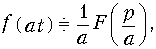
где а — постоянный вещественный коэффициент. Свойство (7.9) легко доказывается путем замены независимой переменной t = atв прямом преобразовании Лапласа (7.2).
Смещение в области действительного переменного (теорема запаздывания)
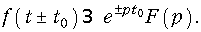
Для доказательства (7.10) введем следующие обозначения:
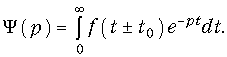
Осуществим замену переменной t = t ± t0.
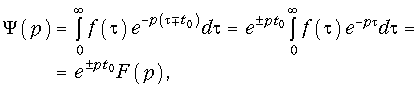
что и требовалось доказать.
Из соотношения (7.10) следует, что сдвиг оригинала по оси времени на t0 соответствует умножению изображения на 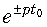 .
.
Смещения в области комплексного переменного (теорема смещения)
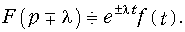
Теорема (7.11) следует непосредственно из прямого преобразования Лапласа, если в (7.2) вместо f(t) подставить 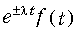 . Причем l может быть как действительной, так и комплексной величиной.
. Причем l может быть как действительной, так и комплексной величиной.
Дифференцирование и интегрирование оригинала по параметру (свойство коммутативности)
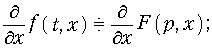
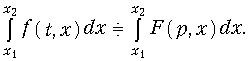
Для доказательства свойств (7.12), (7.13) достаточно продифференцировать или проинтегрировать прямое преобразование Лапласа (7.2) по параметру х.
Произведение изображений
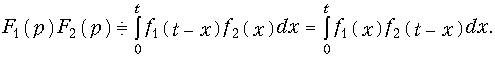
Интегралы в (7.14) носят название свертки функций f1(t) и f2(t).
Дифференцирование изображения
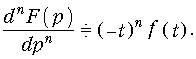
Свойство (7.15) легко доказывается путем дифференцирования прямого преобразования Лапласа (7.2).
Интегрирование изображения
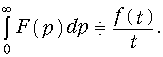
Данное свойство доказывается аналогично (7.15).
В заключение приведем предельные соотношения для оригинала и изображения:
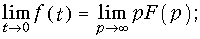
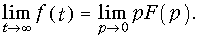
Действительно, согласно свойства дифференцирования оригинала можно записать:

Учитывая, что 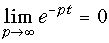 , получаем:
, получаем:
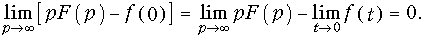
Отсюда непосредственно следует соотношение (7.17). Аналогично доказывается равенство (7.18).
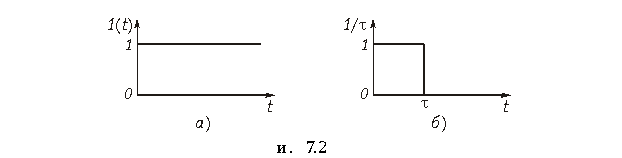
В качестве примера найдем изображение по Лапласу типовых сигналов. Для теоретических и экспериментальных исследований характеристик электрических цепей и передачи сообщений по каналам связи используются различные типы сигналов: гармонические колебания, уровни постоянных напряжений, последовательность прямоугольных импульсов и так далее. Особо важную роль в теоретических исследованиях электрических цепей играют испытательные сигналы в форме единичной функции 1(t) и единичной импульсной функции d(t) (функция Дирака).
Единичная функция
Единичная функция задается уравнением (рис. 7.2, а)
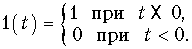
Изображение функции (7.19) будет равно:
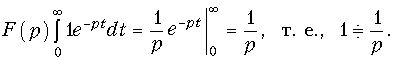
Единичная импульсная функция (функция Дирака)
Эта функция называется еще d-функцией; она задается уравнением
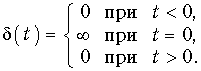
Функция Дирака является физически нереализуемой математической абстракцией, однако обладает рядом интересных свойств и играет очень важную роль в теоретических исследованиях. Формально она может быть получена, например, предельным переходом (при t ® 0) единичного импульса (см. рис. 7.2, б), площадь которого равна единице:

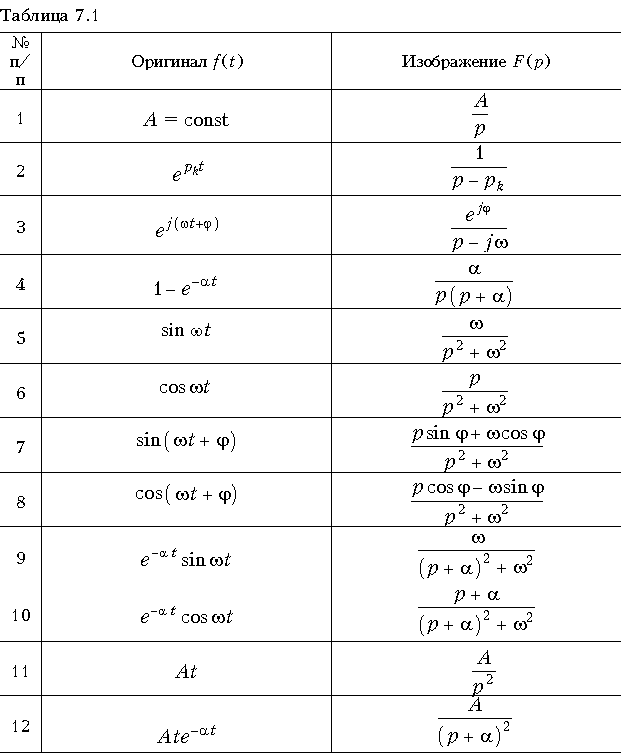
Одним из интересных свойств функции d(t) является ее фильтрующее свойство, определяемое равенством (рис. 7.3):
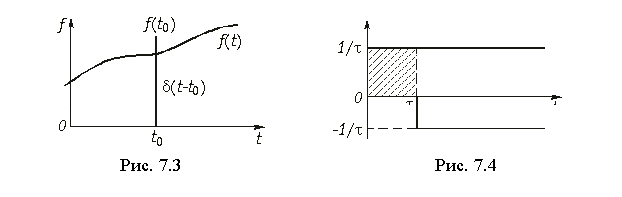
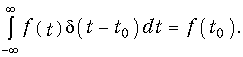
Найдем изображение единичной импульсной функции в форме изображения разности двух единичных функций величины 1(t), сдвинутых друг относительно друга на t (рис. 7.4). Для этих функций с учетом теоремы запаздывания имеем:
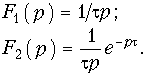
Для результирующего изображения с учетом свойства линейности получим
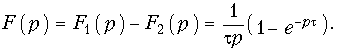
Устремив t ® 0, найдем изображение единичной импульсной функции (d-функции): 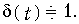
Экспоненциальный сигнал 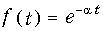 при t > 0:
при t > 0:
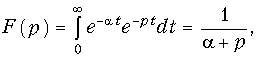
т. е.
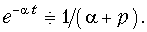
Подобным же образом можно найти изображение по Лапласу других функций, удовлетворяющих условию (7.3). В литературе имеются специальные справочники, в которых приведены оригиналы и изображения широкого класса функций. В табл. 7.1 приведены оригиналы и их изображения наиболее часто встречающихся в теории электрических цепей функций.
7.2. Теорема разложения
Для нахождения оригинала по изображению можно воспользоваться либо таблицами, либо использовать обратное преобразование Лапласа (7.4). Однако вычисление оригинала с помощью (7.4) обычно оказывается весьма сложным. Поэтому, для упрощения расчетов применяют теорему разложения, которая позволяет при нахождении оригинала заменить операцию интегрирования в (7.4) операцией суммирования, что значительно упрощает вычисления. Наиболее строгий вывод этой теоремы можно осуществить на основании теоремы вычетов. Здесь мы ограничимся выводом формул разложения применительно к изображению, представляющему собой рациональную дробь:
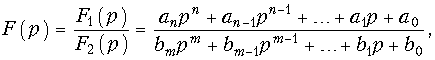
где 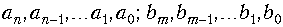 — вещественные коэффициенты, причем F1(p) и F2(p) не имеют общих корней.
— вещественные коэффициенты, причем F1(p) и F2(p) не имеют общих корней.
Для нахождения оригинала f(t) разложим F(p) на простые дроби:
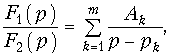
где pk — простые корни характеристического уравнения
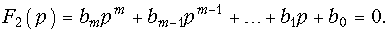
Ak — коэффициенты разложения.
Для того, чтобы найти коэффициент Ak домножим обе части (7.26) на (р — pk) и перейдем к пределу:
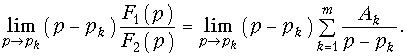
Раскрывая неопределенность в левой части равенства (7.28) по правилу Лопиталя и учитывая, что согласно (7.27) правая часть (7.28) равна Ak, получаем
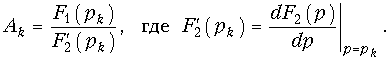
Подставив значения Ak в формулу (7.26), найдем:
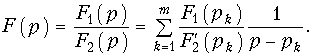
Если учесть, что изображение 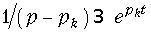 (см. табл. 7.1), то на основании свойства линейности преобразования Лапласа окончательно получим:
(см. табл. 7.1), то на основании свойства линейности преобразования Лапласа окончательно получим:
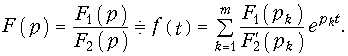
Формула (7.30) является математической формулировкой теоремы разложения и позволяет найти оригинал по изображению в виде (7.25), в случае простых корней. Если среди корней pk имеется один нулевой корень, т. е. F2(р) = pF3(p), то теорема разложения примет вид
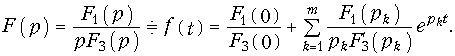
Формулу (7.31) можно получить, если подставить в (7.30) вместо F2(р) значение pF3(р) и осуществить операцию дифференцирования.
Если среди корней уравнения (7.27) (полюсов функции F(p)) имеются комплексно-сопряженные корни pk и pk+1, то в формуле (7.30) достаточно взять pk, а для pk+1 взять сопряженное значение, при этом сумма соответствующая двум этим корням с учетом действительности f(t) будет равна
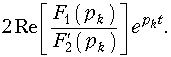
При этом в уравнении для f(t) появятся составляющие типа (6.9): 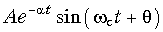 .
.
Теорему разложения можно обобщить и на более общие случаи. В частности, если среди полюсов (7.25) имеются полюса кратности l, то в оригинале f(t) появятся слагаемые типа (6.8).
Пример. Задано изображение в виде
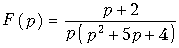 .
.
Обозначим F1(p) = p + 2; F2(p) = p(p2 + 5p + 4). При этом получим F(p) в виде (7.25). Найдем корни характеристического уравнения F2(p) = p(p2 + + 5p + 4) = 0.
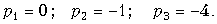
При этом F1(p1) = 2; F1(p2) = 1; F1(p3) = –2.
Определим производную
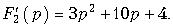
Отсюда F2¢(p1) = 4; F2¢(p2) = –3; F2¢(p3) = 12. Воспользовавшись формулой (7.30), окончательно получим:
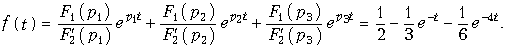
Учитывая, что среди корней характеристического уравнения F2(p) = 0 имеем один нулевой корень, при нахождении f(t) можно было воспользоваться и формулой (7.31). Действительно, если обозначим
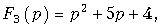
то получим
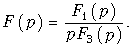
Тогда корни уравнения F3(p) = 0 будут равны p1 = —l, p2 =—4. С учетом значений
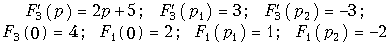
согласно (7.31) окончательно получим
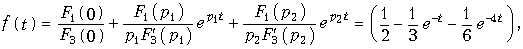
что полностью совпадает с ранее полученным решением.
7.3. Расчет переходных процессов операторным методом
Пользуясь основными свойствами преобразования Лапласа, можно получить основные законы теории цепей в операторной форме. Рассмотрим, например, последовательный RLC-контур (см. рис. 6.14), находящийся при ненулевых начальных условиях uC(0–) ¹ 0; iL(0–) ¹ 0. Для этого контура уравнение по ЗНК имеет вид:
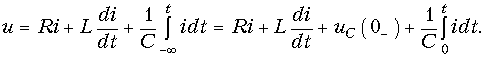
Применив к (7.33) прямое преобразование Лапласа и принимая во внимание свойства линейности, дифференцирования и интегрирования оригинала получим:
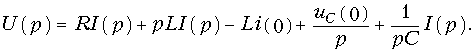
Отсюда получаем закон Ома в операторной форме для данной цепи:
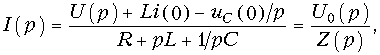
где U0(p) = U(p) + Li(0) — uC(0)/p носит название операторного напряжения; Z(p) = R + pL + 1/pC — операторного сопротивления цепи. Если в Z(p) заменить р на jw, то получим комплексное сопротивление цепи. Величины Li(0) и uC(0)/p называют расчетными напряжениями. Они характеризуют энергию магнитного и электрического полей, запасенную в L и С к моменту коммутации. Величина, обратная Z(p) называется операторной проводимостью цепи:
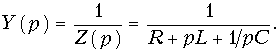
Для нулевых начальных условий закон Ома примет вид
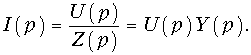
Аналогичным образом можно получить законы Кирхгофа в операторной форме:
первый закон (ЗТК)
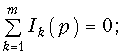
второй закон (ЗНК)
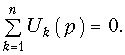
Таким образом, закон Ома и законы Кирхгофа в операторной форме аналогичным этим же законам в комплексной форме (см. (3.48)—(3.50)) с той лишь разницей, что в (7.37) в каждой из п ветвей при наличии ненулевых начальных условий действуют дополнительные расчетные источники Lkik(0) и —uCk(0)/р, положительное направление которых совпадает с выбранным положительным направлением тока в этой ветви.
Используя законы Ома и Кирхгофа в операторной форме, можно найти изображения искомых токов и напряжений в цепи. Для определения оригиналов токов и напряжений можно воспользоваться либо таблицами оригиналов и изображений, либо применить теорему разложения.
Для иллюстрации основных теоретических положений найдем операторным методом закон изменения тока в последовательном RLC-контуре при включении его на источник постоянного напряжения. Уравнение для изображения тока можно найти по закону Ома для нулевых начальных условий (7.35) с учетом изображения постоянного напряжения U(p) ![]() U/p:
U/p:
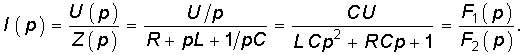
Найдем корни характеристического уравнения
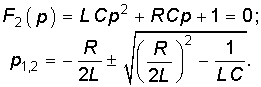
При R > 2r корни будут вещественны и различны. Для нахождения оригинала тока i(t) воспользуемся теоремой разложения (7.30). Для этого найдем производные F2¢(p1) и F2¢(p2):
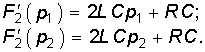
Подставив значения F1(p) = F1(p2) = CU и F2¢(p1) и F2¢(p2) в (7.30) получим оригинал тока
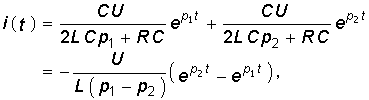
что полностью совпадает с ранее полученным уравнением (6.68).
Из рассмотренного примера хорошо видны преимущества операторного метода: простота, отсутствие громоздких операций по определению постоянных интегрирования. Следует подчеркнуть, что базируясь на законах Ома и Кирхгофа в операторной форме, можно рассчитать переходный процесс любым из ранее рассмотренных методов: контурных токов, узловых напряжений и др. При этом удобно пользоваться эквивалентными операторными схемами. При составлении эквивалентных операторных схем источники тока и напряжений i(t) и u(t) заменяются соответствующими изображениями I(p) и U(p), индуктивность L заменяется на pL, а емкость С — на 1/pC при нулевых начальных условиях. Если начальные условия ненулевые, то последовательно с pL добавляется источник напряжения Li(0), а с С — источник напряжения — uC(0)/р (рис. 7.5)
* Возможны схемы замещения заряженной емкости uC(0) и индуктивности с током iL(0) с помощью источников тока с задающими токами CuC(0) и iL(0)/p соответственно.
Например, эквивалентная операторная схема для цепи, изображенной на рис. 6.17, будет иметь вид (рис. 7.6). Составив для этой схемы уравнения по законам Кирхгофа в операторной форме, получим систему алгебраических уравнений, решение которых существенно проще системы (6.86).
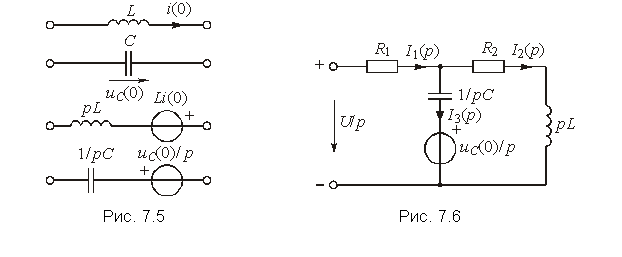
Операторный метод можно использовать и для решения уравнения состояния цепи. При этом уравнение состояния (6.94) с учетом свойств дифференцирования оригинала и линейности преобразования Лапласа примет вид:
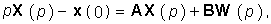
где Х(р), W(p) — изображения векторов состояния x(t) и входных воздействий W(t).
Из (7,38) получаем непосредственно решение
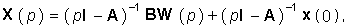
где I — единичная матрица. Применив к (7.39) теорему разложения, можно получить искомый вектор состояния
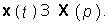
7.4. Операторные передаточные функции
Важную роль в методах анализа и синтеза электрических цепей при нулевых начальных условиях играют операторные передаточные функции, которые определяются как отношение изображения выходной реакции цепи к изображению входного воздействия. В соответствии с этим определением различают четыре вида передаточных функций:
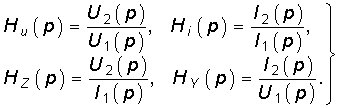
где Ни(р), Hi(p) имеют смысл операторных передаточных функций по напряжению и току; НL(р); НY(р) —операторные передаточные сопротивление и проводимость соответственно.
Если в (7.40) заменить оператор р на jw, то получим уравнение комплексных передаточных функций Н(jw), широко используются при частотных методах анализа электрических цепей.
Зная передаточную функцию цепи Н(р), с помощью (7.40) нетрудно найти изображение реакции цепи, а следовательно, и саму реакцию на заданное воздействие.
Операторную передаточную функцию Н(р) для пассивной цепи можно представить как дробно-рациональную функцию с вещественными коэффициентами:
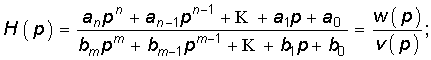
или в виде
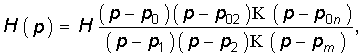
где p01, p02, ..., p0n — нули; p1, p2, ..., pm — полюсы передаточной функции; Н = аn/bm.
Степени полиномов числителя п и знаменателя т зависят от числа реактивных элементов пассивной цепи.
Заменив в (7.41) оператор р на jw, получим комплексную передаточную функцию цепи
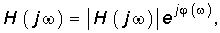
где АЧХ цепи
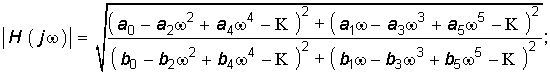
ФЧХ цепи
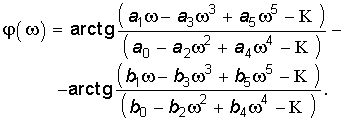
Учитывая, что согласно (7.43) |H(jw)| является иррациональной, обычно при анализе и синтезе цепей имеют дело с квадратом АЧХ:
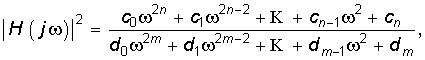
где коэффициенты сk и dk получаются путем объединения коэффициентов при одинаковых степенях переменной w.
Перечислим основные свойства операторных передаточных функций и квадрата АЧХ пассивных цепей:
1. Передаточная функция является дробно-рациональной функцией с вещественными коэффициентами. Вещественность коэффициентов объясняется тем, что они определяются элементами схемы.
2. Полюсы передаточной функции располагаются в левой полуплоскости комплексной переменной р. На расположение нулей ограничений нет. Докажем это свойство на примере передаточной функции Ни(р) = U2(р)/U1(р). Выберем входное воздействие u1(t) = d(t) или в операторной форме U(р) = l. Изображение выходного напряжения U2(р) = U1(р)Ни(р) в этом случае численно равно Ни(р), т. е.
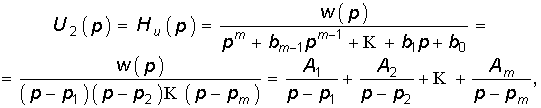
где w(p) — полином числителя передаточной функции; A1, A2, ..., Am, —коэффициенты разложения дробно-рациональной функции на сумму простых дробей.
Перейдем от изображения U2(p) к оригиналу u2(t):
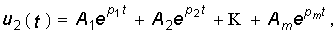
где в общем случае pi = ai + jwi.
В пассивных и устойчивых активных четырехполюсниках колебания на выходе четырехполюсника после прекращения воздействия должны иметь затухающий характер. Это означает, что в (7.46) вещественные части полюсов pi должны быть отрицательными (ai < 0), т. е. полюсы должны находиться в левой полуплоскости переменной р.
3. Степени полиномов числителей передаточной функции и квадрата АЧХ не превышают степеней полиномов знаменателей, т. е. п < т. Если бы это свойство не выполнялось, то на бесконечно больших частотах АЧХ принимала бы бесконечно большое значение (так как числитель рос бы с увеличением частоты быстрее знаменателя), т. е. цепь обладала бы бесконечным усилением, что противоречит физическому смыслу.
4. Квадрат АЧХ является четной рациональной функцией переменной w с вещественными коэффициентами. Это свойство с очевидностью вытекает из способа получения квадрата АЧХ по передаточной функции.
5. Квадрат АЧХ не может принимать отрицательных и бесконечно больших значений при w > 0. Неотрицательность 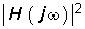 следует из свойств квадрата модуля комплексной величины. Конечность значений АЧХ на реальных частотах объясняется так же, как и в свойстве 3.
следует из свойств квадрата модуля комплексной величины. Конечность значений АЧХ на реальных частотах объясняется так же, как и в свойстве 3.
7.5. Вопросы и задания для самопроверки
1. В чем заключается сущность операторного метода расчета цепи?
2. Что такое операторное сопротивление цепи?
3. Что такое операторные схемы замещения при составлении эквивалентной операторной схемы?
4. 
Чем заменяются индуктивности и емкости в операторной схеме замещения?
5. Как учитываются независимые начальные условия?
6. Записать закон Ома и законы Кирхгофа в операторной форме.
7. Что такое единичная функция и d-функция?
8. Что понимается под операторной передаточной функцией? Каковы ее свойства?
9. Каким образом можно перейти от изображения к оригиналу?
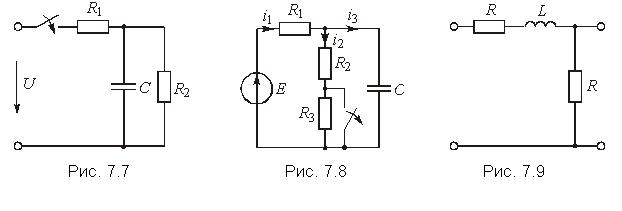
10. Для схемы, изображенной на рис. 7.7, операторным методом определить напряжение на конденсаторе uC(t). U = 20 В; R1 = = R2 = 100 Ом; С = 4 мкФ.
Ответ: uC(t) = 10 – 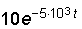 , В.
, В.
11. Для схемы, изображенной на рис. 7.8, найти изображение тока I2(p).
Ответ: I2(p) = 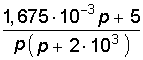 .
.
12. Зная изображение тока (рис. 7.8), определить оригинал i2(t).
Ответ: i2(t) = 2,5 – 0,825 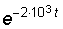 .
.
13. Для схемы, изображенной на рис. 7.9, определить: 1) операторную передаточную функцию Hu(p); 2) найти АЧХ цепи. Ответ: