8.1. Необходимость рассмотрения граничных условий

8.2. Граничные условия для векторов ЭМП

8.3. Отражение электромагнитных волн при нормальном падении на плоскую границу раздела

8.4. Наклонное падение ЭМВ. Формулы Френеля

8.5. Угол Брюстера

8.6. Явление полного внутреннего отражения

8.7. Поверхностный эффект на границах раздела

8.1. Необходимость рассмотрения граничных условий

В реальной жизни неизбежно появляются препятствия на пути распространения ЭМВ. Что же происходит при этом ?

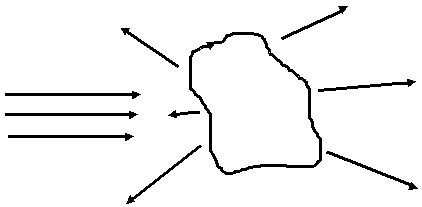
В этом случае задача чрезвычайно сложная. В частном случае еще можно. Для ЭМВ также как и для оптических имеет место рассеяннее, дифракция. В качестве препятствия рассмотрим случай простейший (бесконечно большое препятствие).

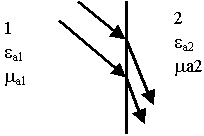
Уравнения Максвелла дают информацию о поведении полей с непрерывным изменением проницаемости:

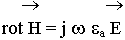
1) Уравнения Максвелла из-за разрыва проницаемостей нельзя применять к точкам, лежащим на границе раздела. Информацию о поведении полей на границе мы будем получать из дополнительных условий, их называют граничными условиями.

2) Решение уравнений Максвелла всегда записывается с точностью до const, чтобы const эту получить надо знать дополнительные условия. В качестве таких условий используют граничные условия. При формировании граничных условий удобно любой вектор разлагать на составляющие.

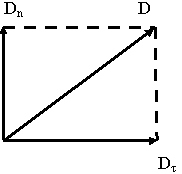
В дальнейшим для поля произвольно ориентированного к границе раздела будем выделять нормальную и касательную составляющие. Граничные условия отдельно записываются для нормальных и касательных составляющих.

8.2. Граничные условия для нормальных составляющих векторов электрического поля

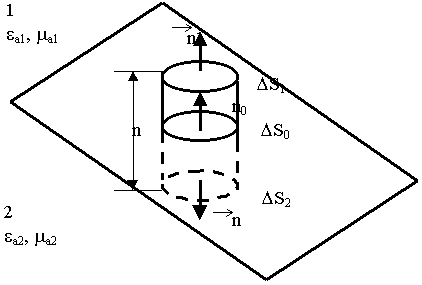
Для выяснения граничных условий используем интегральное соотношение. Выделим площадку небольших размеров. Формируем замкнутую поверхность (цилиндрическую). Применим к этой поверхности т. Гаусса:

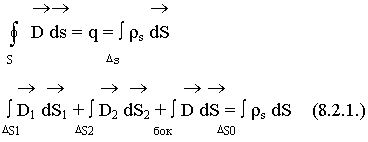
Предположим, что размеры площадок равны и достаточно малы, что в пределах этих площадок вектор D не меняется:

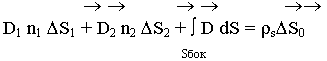
Осуществляем предельный переход, когда:

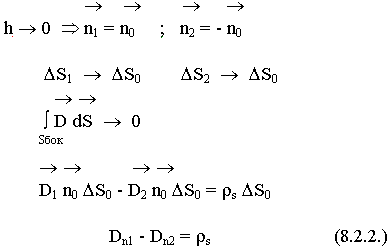
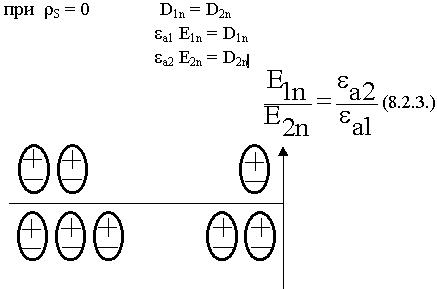
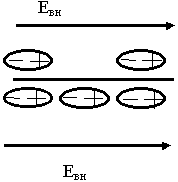
На границе раздела нормальные составляющие терпят разрыв (изменяются скачком) на величину 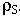. Почему происходит скачок, с физической точки зрения ? Предположим на каждую из сред действуют силы Е_вн. Каждая среда имеет диполи. Эти диполи под воздействием поля будут ориентироваться. На границе раздела появились нескомпенсированные положительные заряды, которые создают поле свое.

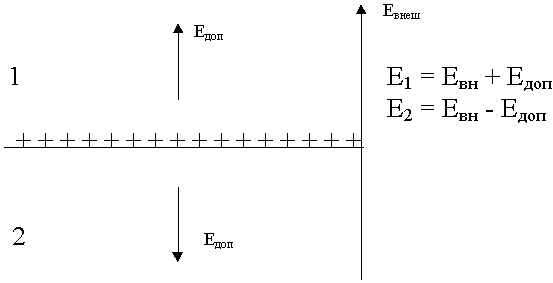
Граничные условия для касательных составляющих векторов электрического поля

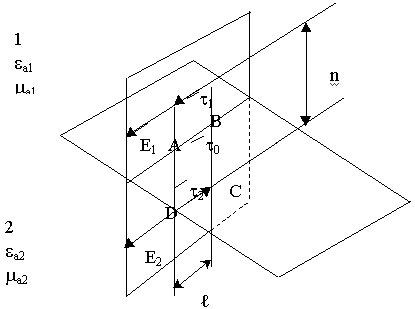
В плоскости Р построим контур, часть которого находится в нижней среде, часть в верхней. К контуру АBCD применим закон электромагнитной индукции:

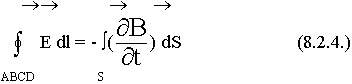
Условие: 1) направление обхода контура.

2) ориентация касательных векторов.

1. Левую часть при вычислении интеграла разобьем на части:

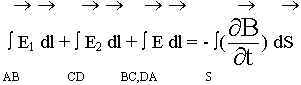
размеры контура малы, значение поля в пределах контура не меняются:

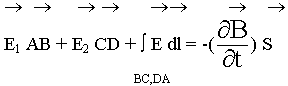
2. Стягиваем контур, устремим высоту контура к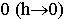

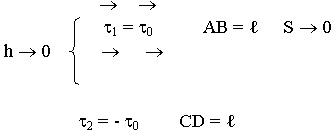
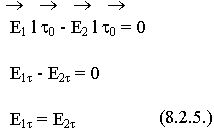
Касательные составляющие вектора Е непрерывны при переходе через границу раздела.

1. Результирующий заряд на границе равен 0 (граница не заряжена).

Рассмотрим границу раздела, состоящую из двух сред. Пусть поле (во второй среде) приложено параллельно границе в первой среде тоже параллельно.

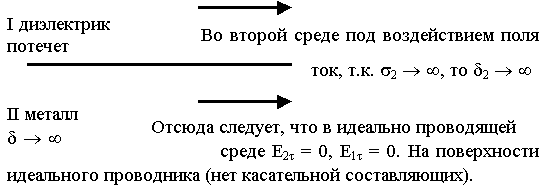
На поверхности идеального проводника есть только нормальные составляющие:

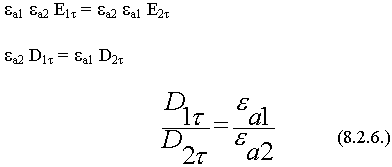
Касательные составляющие вектора D изменяются скачком.

Граничные условия для нормальных составляющих векторов магнитного поля.

Картинка такая же, как для нормальных составляющих электрического поля.

Применяем к поверхности теорему Гаусса для магнитного поля.

Нормальные составляющие вектора В непрерывны на границе раздела.

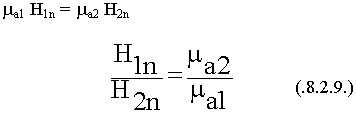
Нормальные составляющие вектора Н изменяются скачком

при переходе через границу на величину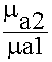

Граничные условия для касательных составляющих магнитного поля.

Построение рис. совпадает со случаем для касательных составляющих вектора Е. Применяя к контуру ABCD закон полного тока (при I_пол = 0) имеем:

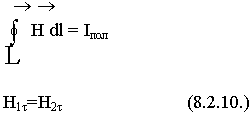
Касательные составляющие вектора Н непрерывны:

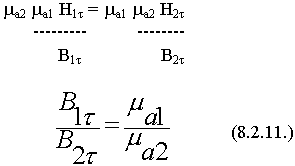
Касательные составляющие вектора В при переходе через границу изменяется скачком на величину 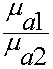. Физическое объяснение вытекает из свойств сред.

8.3. Нормальное падение плоской волны на плоскую границу раздела

Предположим, что имеется граница раздела (бесконечно плоская граница). На эту границу падает волна.

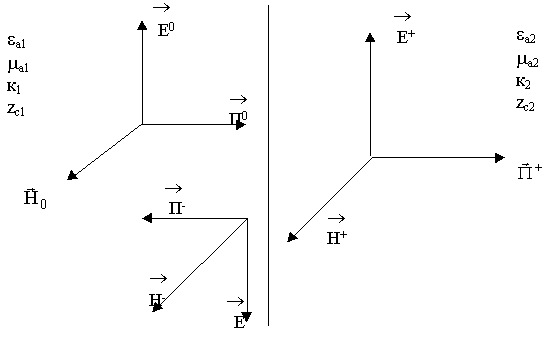
Часть волны будет отражаться, часть пройдет во вторую среду. Для отраженной волны один из векторов, либо вектор Е либо Н, должен изменить направление. Какой ? Пока еще не можем сказать какой. Ответ будет чуть позже. Анализ:

1. Запишем исходные составляющие полей в каждой среде в общем виде:

во второй среде

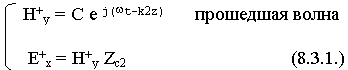
Как определить амплитуды А, В, С ? Считаем, что на границу падает волна с известной амплитудой А. Чтобы определить неизвестные амплитуды, воспользуемся граничными условиями. Для данной задачи используем граничные условия для касательных составляющих магнитных полей 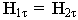, для электрических полей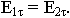

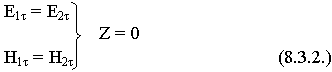
В первой среде суммарные электрическое и магнитное поля (падающие и отраженные волны).

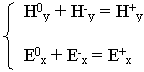
При переходе через границу раздела координатная составляющая е ^jkz исчезает, т.к.

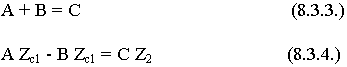
Коэффициент отражения R определяют как отношение амплитуды отраженной волны электрического поля к амплитуде падающей волны электрического поля. Можно и для магнитного поля, это непринципиально, изменится только знак:

R =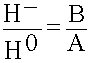

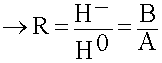
Коэффициент прохождения Т определяют как отношение амплитуды прошедшей волны к амплитуде падающей волны:

Т = 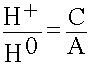разделим (8.3.3) на А. (8.3.5.)

(8.3.4.) разделим на Z_cА:

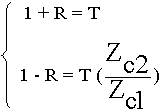
Сложим:

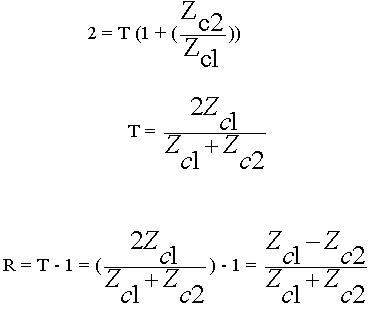
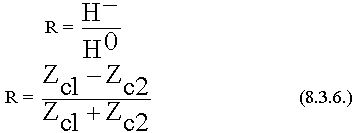
Анализ полных выражений

Мы установили, что коэффициент отражения зависит только от свойств cреды:

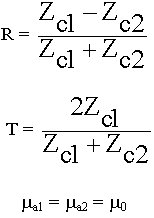
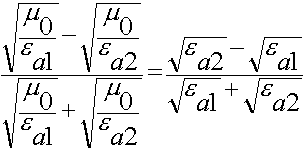
Выводы:

• Отражение волн происходит от оптически более плотной среды 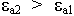. У отраженной волны ориентация вектора Е изменяется на 180⁰.
• Отражение от оптически менее плотной среды вода/воздух . Вектор Е сохраняет свою ориентацию в отраженной волне, у отраженной волны будет изменяться вектор Н на 180⁰.
• Режим согласования сред. Всегда режиму согласованных сред соответствует требование, что отраженной волны нет.
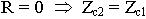
• Режим полного отражения.

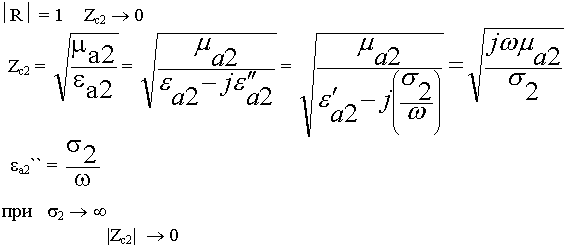
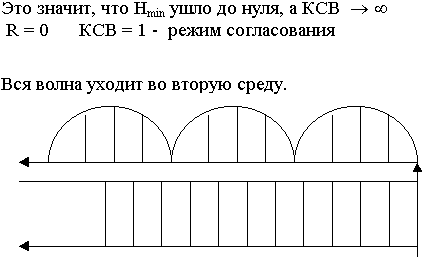
Полное отражение можно получить от границы раздела с большой проводимостью. Выясним особенности распределения ЭМП в первой среде. Результирующее поле является суммой двух волн:

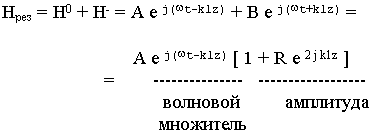
Амплитуда в результирующем поле зависит от координаты Z.

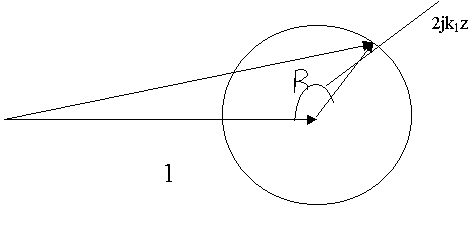
Воспользуемся методом векторного сложения:

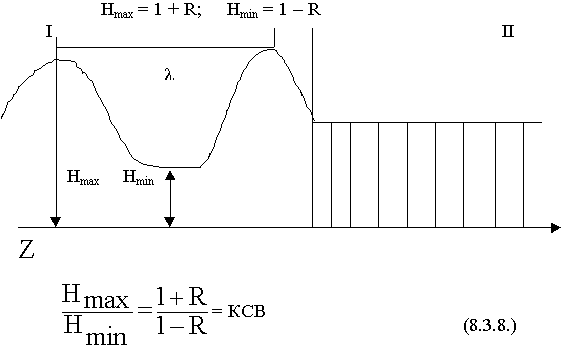
В линиях передачи протекают точно такие же физические процессы по таким же закономерностям. Выясним чему равно расстояние между соседними пучностями поля.

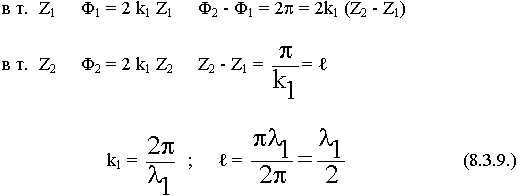
Вывод: измеряя расстояние между двумя узлами и удвоив его, получим длину волны.

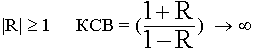
8.4. Наклонное падение волны на плоскую границу раздела двух сред

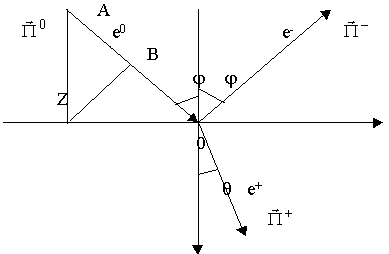
Выясним угловые соотношения при наклонном падении:

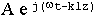- направление распространения волны совпадает с осью Z.

Отсчет пути проходимого волной проводится в направлении движения волны:

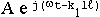- для падающей волны.

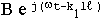- для отраженной волны.

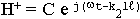- прошедшая волна.

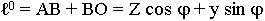
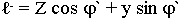
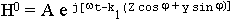
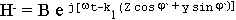
Воспользуемся граничными условиями задачи для касательных составляющих полей:

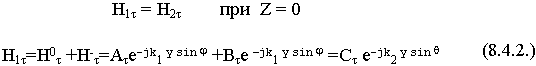
А, В, С - произвольные амплитуды.

Это условие должно выполняться при любом значении у, т.е. показатели всех экспонент должны быть равны. Из этого автоматически следует:

Для идеальной среды проницаемости являются const и тогда второй закон Снеллиуса не зависит от частоты.

Выводы:

• Законы Снеллиуса не зависят от поляризации падающей волны.
• Первый закон Снеллиуса справедлив для любых частот.

Второй закон:

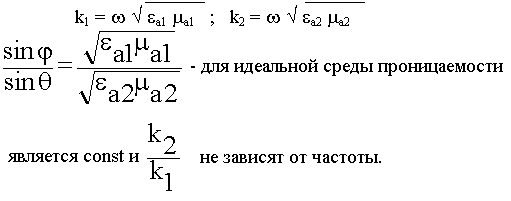
Если среда реальная:

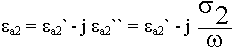
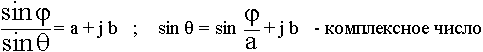
Для сред с потерями геометрическое толкование второго закона Снеллиуса теряет смысл.

Амплитудные соотношения при наклонном падении. Формулы Френеля.

Амплитуды отраженных и прошедших волн зависят от поляризации падающих волн. Будем различать 2 вида поляризации:

• Горизонтальная поляризация падающей волны.

Вектор параллелен границе раздела двух сред.

• Вертикальная поляризация падающей волны. Вектор

параллелен границе раздела двух сред.

Горизонтальная поляризация падающей волны.

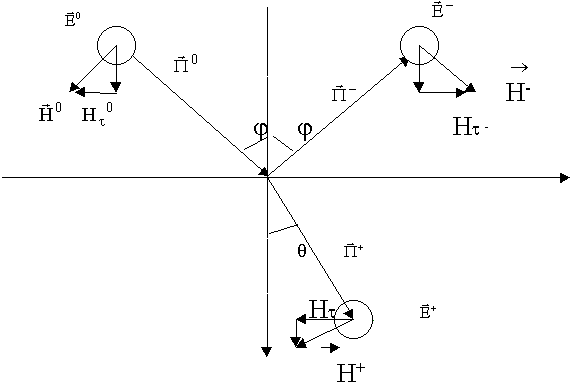
Чтобы определить амплитуды, потребуем выполнения граничных условий. Поскольку Е параллелен границе раздела, потребуем выполнения граничных условий по касательным составляющим:

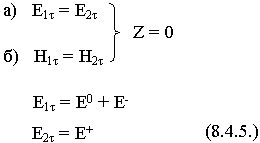
Выделим в магнитном поле касательные составляющие:

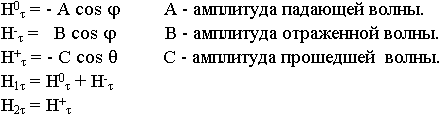
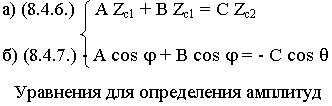
Введем понятие коэффициента отражения в случае горизонтальной поляризации, лучше через электрические поля, т.к. вектор не меняет ориентации.

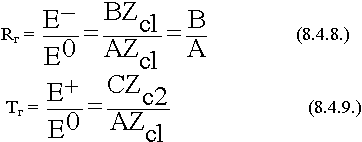
Т_г - коэффициент прохождения.

Разделим на A Z_c1 уравнение (8.4.6.), а на A cos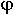; уравнение (8.4.7.):

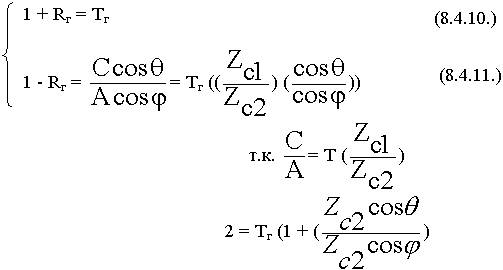
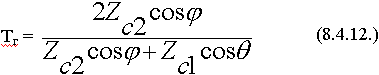
Из уравнения (8.4.10.) определяем:

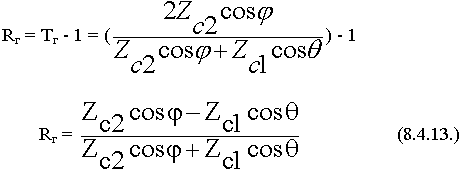
Формулы Френеля для горизонтальной поляризации.

Вертикальная поляризация.

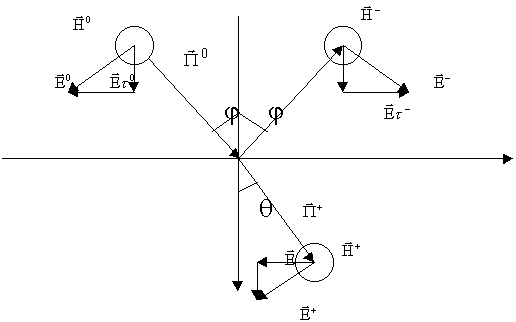
Воспользуемся принципом перестановочной двойственности ():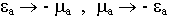

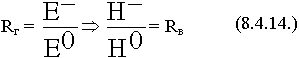
Вектор не меняет ориентацию, удобно через Н.

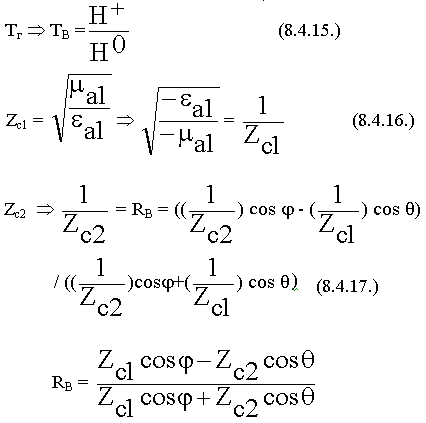
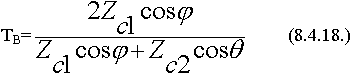
Может ли в случае наклонного падения вся волна проходить во вторую среду без отражения?

8.5. Согласование при наклонном падении. Угол Брюстера

Условие согласования при наклонном падении соответствует требованию, чтобы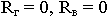

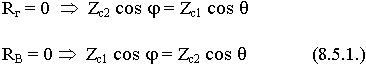
Видно, что условие согласования зависит от угловых соотношений и от свойств среды.

Качественно:

1) При распространении волны в немагнитном диэлектрике.

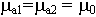для волны с горизонтальной поляризацией режим согласования никогда не подобрать, т.е. нет такого угла 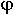, при котором условие бы это выполнялось.

Качественно. Под воздействием приложенного поля диполи будут ориентироваться по полю. Такие диполи излучают перпендикулярно своей оси, часть энергии вверх, часть вниз (прошедшая волна).

2) для волны с вертикальной поляризацией можно подобрать такой угол, при котором вся волна перейдет во вторую среду, т.к. параллельно своей оси диполь не излучает.

1)

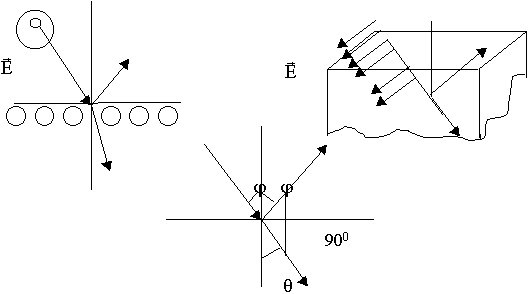
Из анализа - направление диполя параллельно отраженной волне.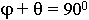

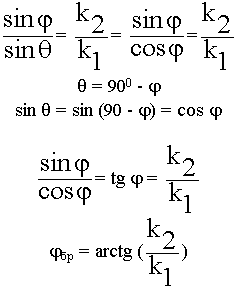
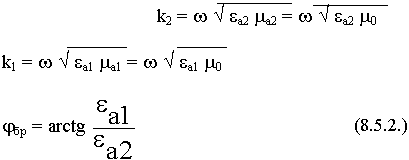
В случае немагнитных диэлектриков режим согласования при наклонном падении выполняется в случае вертикальной поляризации.

8.6. Полное внутреннее отражение

Выясним, при каких условиях имеет место полное отражение волны от границы раздела при наклонном падении.

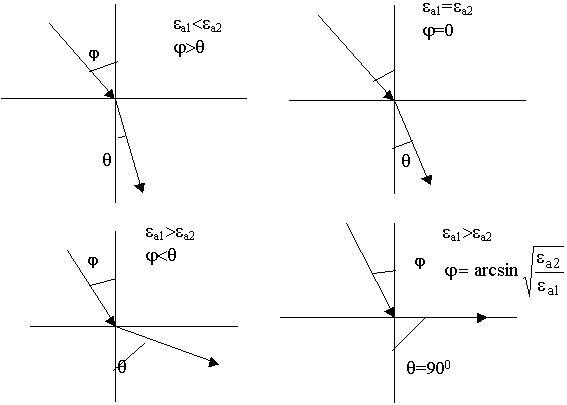
Угол 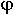, при котором прошедшая волна идет вдоль границы раздела получил название - угол полного внутреннего отражения, а явление распространения называется полным внутренним отражением. Явление полного внутреннего отражения реализуется, когда волна распространяется из более плотной cреды в менее плотную.

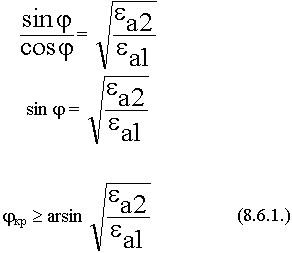
Отражение происходит от границы раздела двух диэлектриков, металл не требуется, подобраны углы и параметры сред.

Для явления полного внутреннего отражения характерно:

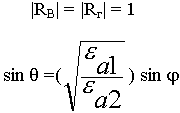
можно сделать 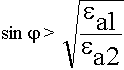тогда sin 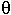> 1 ? Неясно, что такое 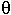, когда sin 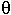> 1.

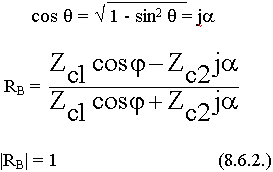
Условию полного внутреннего отражения соответствует полное отражение волны от границы раздела аналогично | R_г| = 1.

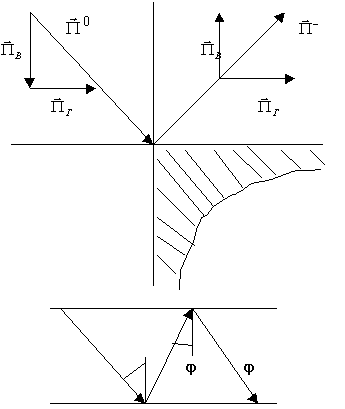
При выполнении режима полного внутреннего отражения энергия волны распространяется вдоль границы (поверхности) раздела, а во второй среде экспоненциально убывает. Волну называют поверхностной. Подошли к таким линиям как световод, к этому вернемся позже.

8.7. Поверхностный эффект при наклонном падении

Поверхностный эффект проявляется в резком изменении амплитуды поля вблизи границы раздела сред, при этом одна из сред обладает большой

проводимостью (на поверхность металла, влажную почву, морскую воду). Предположим, что плоская ЭМВ с произвольной поляризацией падает на хорошо проводящую поверхность.

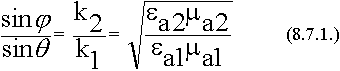
При достаточно большом значении 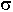среды, прошедшая во вторую среду волна будет распространяться по нормали ( очень мал).

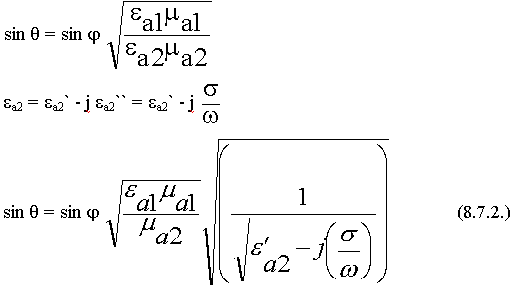
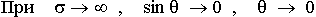
Амплитуда поля уменьшается очень быстро, т.к. 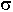велика, 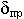- тоже очень сильно убывает. 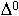– глубина проникновения. Это расстояние, на котором амплитуда поля убывает в е раз.

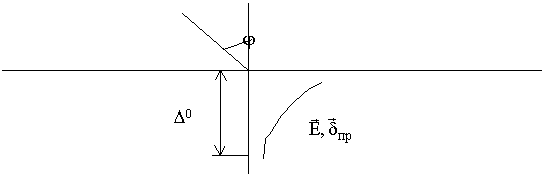
Можно обобщить это и на металлический проводник. Поверхностный эффект проявляется в проводнике. Центральную часть можно убрать, т.к. ток протекает в тонком слое (при постоянном токе, он распределяется по сечению). Поверхностный эффект приводит к увеличению сопротивления провода и уменьшению индуктивности.

Неприятности. В тонком поверхностном слое сильная плотность тока, сильный разогрев.