Можно воспользоваться обратным z-преобразованием (подобно тому как мы пользуемся обратным преобразованием Лапласа):
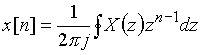 ,
,
где интегрирование ведется по замкнутому контуру в z-плоскости.
Другой способ заключается в том, чтобы разложить функцию ![]() в степенной ряд по степеням
в степенной ряд по степеням ![]() . Тогда коэффициенты при степенях
. Тогда коэффициенты при степенях ![]() будут, в соответствии с формулой (13), отсчетами дискретного сигнала
будут, в соответствии с формулой (13), отсчетами дискретного сигнала ![]() .
.
Пример 10.1. Найдем дискретный сигнал ![]() , которому соответствует z-преобразование
, которому соответствует z-преобразование 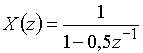 .
.
Воспользуемся разложением функции ![]() в ряд
в ряд ![]()
![]() .
.
Для заданного z-преобразования ![]() , поэтому запишем z-преобразование в виде
, поэтому запишем z-преобразование в виде
![]() .
.
Сравнивая полученное выражение с общей формулой z-преобразования 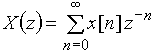 , записываем последовательность
, записываем последовательность
![]() {1; 0,5; 0,25; 0,125; ...}.
{1; 0,5; 0,25; 0,125; ...}.
Общий член этой последовательности ![]() .
.
Пример 10.2. Найдем отсчеты дискретного сигнала по его z-преобразованию
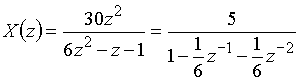 .
.
Для разложения функции ![]() в степенной ряд по степеням
в степенной ряд по степеням ![]() выполним деление числа 5 на многочлен
выполним деление числа 5 на многочлен 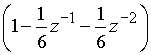 . В результате получим частное
. В результате получим частное ![]() . Отсчеты дискретного сигнала равны
. Отсчеты дискретного сигнала равны
![]() и т.д.
и т.д.
Процедура деления здесь не приведена из-за ее громоздкости, хотя выражения полиномов, стоящих в числителе и знаменателе ![]() , не слишком сложные.
, не слишком сложные.
Более эффективным способом нахождения ![]() по известному
по известному ![]() является способ подобный методу разложения на простейшие дроби в преобразованиях Лапласа.
является способ подобный методу разложения на простейшие дроби в преобразованиях Лапласа.
Пример 10.3. Найдем общий член ![]() дискретного сигнала
дискретного сигнала ![]() , которому соответствует z-изображение, заданное в примере 10.2
, которому соответствует z-изображение, заданное в примере 10.2
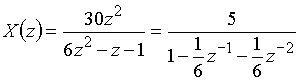 .
.
Функция ![]() имеет полюсы в точках
имеет полюсы в точках ![]() и
и ![]() , или, что то же, в точках
, или, что то же, в точках ![]() и
и ![]() .
.
Разложим ![]() на сумму простых дробей:
на сумму простых дробей:
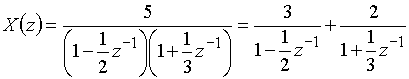 . (16)
. (16)
Коэффициенты в числителях каждой дроби вычисляются так же, как при разложении входного сопротивления ![]() реактивных двухполюсников при синтезе их по схеме Фостера:
реактивных двухполюсников при синтезе их по схеме Фостера:
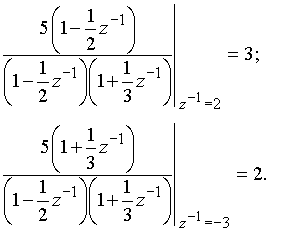
Подобно тому, как формула (15) представляет сумму ряда (14), простые дроби в (16) являются суммами рядов
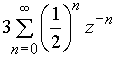 и
и 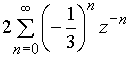 .
.
Поскольку z-преобразование – это линейная операция, то последовательность ![]() состоит из суммы двух последовательностей:
состоит из суммы двух последовательностей:
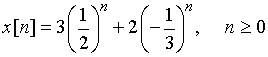 .
.
После выполнения операции возведения в степень n получим отсчеты дискретного сигнала
![]() и т.д.
и т.д.
Самоконтроль
1. Какие способы используются для нахождения дискретного сигнала по его z-преобразованию?
2. Запишите общий член последовательности ![]() , имеющей z-преобразование
, имеющей z-преобразование ![]() .
.
3. Запишите общий член последовательности ![]() , имеющей z-преобразование
, имеющей z-преобразование 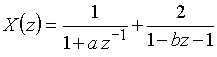 . Найдите значения
. Найдите значения ![]() ,
, ![]() и
и ![]() этой последовательности.
этой последовательности.

