3.1. Основные понятия и определения
3.2. Смежность, инцидентность, степени
3.4. Подграфы. Операции на графах
3.5. Связность. Компоненты связности. Маршруты и пути
3.6. Эйлеровы и гамильтоновы графы
3.8. Цикломатическое число графа. Построение остовного дерева связного графа
3.1. Основные понятия и определения
Граф (от греческого 
- пишу) - непустое множество вершин 
и набор 
неупорядоченных и упорядоченных пар вершин вида (v,w). Обычно граф обозначают как G(V,E); количество вершин и ребер обозначается, соответственно, n(G) и m(G).
Неупорядоченная пара вершин называется ребром {v,w}, упорядоченная пара - дугой (v,w).
Граф, содержащий только ребра, называется неориентированным (обозначается G). Граф, содержащий только дуги - ориентированным (или орграфом) (обозначается 
).
Пара вершин может быть соединена двумя или более рёбрами (или, соответственно, дугами одного направления), такие рёбра (или дуги) называются кратными. Дуга (или ребро) может начинаться и заканчиваться в одной и той же вершине, в этом случае соответствующая дуга (или ребро) называется петлёй.
Граф без кратных рёбер и петель называется простым графом.
Граф, все n вершин которого являются изолированными, называется нулевым (пустым) и обозначается 
.
Простой граф, любые две вершины которого являются смежными, называется полным. Полный граф с n вершинами обозначается 
.
3.2. Смежность, инцидентность, степени
Вершины, соединённые ребром или дугой, называются смежными.
Рёбра, имеющие общую вершину, тоже называются смежными.
Ребро (или дуга) и любая из его вершин называются инцидентными.
Говорят, что ребро {v,w} соединяет вершины v и w. Для орграфов: дуга (v,w) начинается в вершине v (исходит из вершины v) и заканчивается в вершине w (заходит в вершину w), или идет из вершины v в вершину w.
Степенью вершины v графа G называется число deg v рёбер графа G, инцидентных вершине v, при этом петли учитываются дважды. Вершина графа, имеющая степень 0, называется изолированной, а степень 1 - тупиковой (висячей, концевой).
Для орграфа: полустепенью исхода (захода) вершины v орграфа называется число 
(
) дуг орграфа, исходящих из вершины v (заходящих в вершину v), при этом каждая петля, инцидентная вершине v , учитывается как в , так и в .
Теорема. (Теорема о рукопожатиях) Сумма степеней всех вершин графа G равна удвоенному числу его рёбер, то есть: 
. (Число пожатых рук всегда четно.)
Для орграфа: 
.
Доказательство следует из тех соображений, что каждое ребро вносит в сумму вклад 2.
Следствие. В каждом графе число вершин нечётной степени чётно.
3.3. Способы задания графов
- Рисунок.
- Список вершин и рёбер.
- Матрица смежности. Матрицей смежности называется квадратная матрица A(G)=(
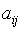), (i,j=1,…,n), у которой элемент 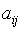равен числу рёбер, соединяющих 
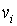и 
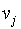
Для орграфа элемент матрицы A(
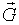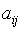), равен числу дуг, идущих из 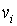в 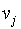. - Матрица инцидентности. Матрицей инцидентности графа G (без петель) называется матрица B(G)=(
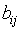) (для орграфа B(
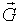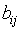)=()) размерности 
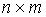, у которой:
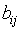=1, если вершина 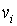инцидентна ребру 
,
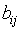=0, в противном случае.
Для орграфа:
=1, если вершина есть начало дуги ;
= - 1, если вершина есть конец дуги ;
=0, если и не инцидентны.
Примеры:
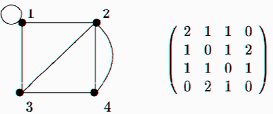
Граф и его матрица смежности.
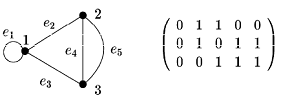
Граф и его матрица инцидентности, здесь вершинам соответствуют строки, а ребрам - столбцы.
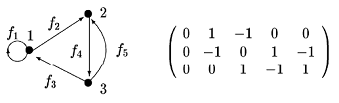
Матрица инцидентности для ориентированного графа, здесь вершинам соответствуют строки, а дугам - столбцы.
3.4. Подграфы. Операции на графах
Подграфом графа G(V,E) называется граф, все вершины и ребра которого содержатся среди вершин и ребер исходного графа G(V,E).
Определим некоторые операции на графах.
Удаление или добавление ребра.
Удаление вершины. Из множества вершин удаляем выбранную вершину, а из множества ребер все инцидентные ей ребра.
Стягивание ребра. Отождествляем (стягиваем) вершины инцидентные выбранному ребру.
Добавление вершины (разбиение ребра). Выберем некоторое ребро (u,v) из множества ребер и удалим его. В множество вершин добавим новую вершину w, а в множество ребер новые ребра (u,w) и (w,v).
Объединение графов. Объединением графов 
и 
называется граф 
.
Пересечение графов. Пересечением графов и (
) называется граф 
.
3.5. Связность. Компоненты связности. Маршруты и пути
Маршрут в графе - это последовательность вершин и рёбер 
, где любые два "соседа" инцидентны. Рёбра и вершины в маршруте могут повторяться. Если начальная и конечная вершины совпадают, то маршрут называется замкнутым. Если все вершины и рёбра маршрута различны, то он называется цепью. Замкнутая цепь - это цикл. Длина маршрута равна числу входящих в него рёбер.
Граф G(V,E) называется связным, если для любых его вершин существует соединяющий их маршрут. Компонентой связности называется максимальный связный подграф графа G(V,E). Число компонент связности графа обозначается k(G).
Ориентированный граф G(V,
) называется сильно связным, если для любых его вершин u и v существуем путь из u в v и путь из v в u.
В этом случае говорят, что вершины u и v достижимы друг из друга.
Если для любых двух вершин u и v графа G(V,) существует маршрут из u в v или из v в u, то граф называется связным или односторонне связным.
Вершина, удаление которой увеличивает число компонент связности, называется точкой сочленения. Ребро, удаление которого увеличивает число компонент связности, называется перешейком (мостом).
3.6. Эйлеровы и гамильтоновы графы
Цикл в графе называется эйлеровым, если он проходит через каждое ребро графа ровно один раз. Граф называется эйлеровым, если в нем есть эйлеров цикл.
Теорема. Граф является эйлеровым тогда и только тогда, когда граф связный и все вершины имеют четную степень.
Теорема. Ориентированный граф является эйлеровым тогда и только тогда, когда он сильно связный и для любой его вершины имеет место равенство: =.
Свое название эйлеровы графы получили в честь Л.Эйлера, который первым рассмотрел такие графы в 1736 году в своей знаменитой работе о кенигсбергских мостах. Этой работой Эйлер, по существу, положил начало новому разделу математики - теории графов.
Задача о кенигсбергских мостах состояла в следующем. На реке Прегель в Кенигсберге было два острова, соединенных между собой и с берегами семью мостами, как показано на рисунке:
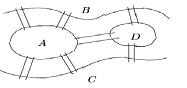
Спрашивается, можно ли, начиная с некоторого места суши, обойти все мосты ровно по одному разу и вернуться в начальную точку? Эйлер предложил рассмотреть следующий граф:
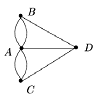
Нетрудно догадаться, что решение этой задачи сводится к поиску эйлеровой цепи в данном графе. Однако, как показывает приведенная теорема, в указанном графе нет эйлеровых цепей.
Цикл в графе называется гамильтоновым, если он проходит через каждую вершину графа ровно один раз. Граф называется гамильтоновым, если в нем есть гамильтонов цикл.
Указанные названия циклов связаны с именем Уильяма Гамильтона, который в 1859 году предложил следующую игру головоломку:
Требуется, переходя по очереди от одной вершины додекаэдра к другой вершине по его ребру, обойти все 20 вершин по одному разу и вернуться в начальную вершину.
Отметим, что придумано еще много других развлекательных и полезных задач, связанных с поиском гамильтоновых циклов. Сформулируем две из них:
1. Кампанию из нескольких человек требуется рассадить за круглым столом таким образом, чтобы по обе стороны от каждого сидели его знакомые.
Очевидно, для решения этой задачи нужно найти гамильтонов цикл в графе знакомств компании.
2. (Задача о шахматном коне.) Можно ли, начиная с произвольного поля шахматной доски, обойти конем последовательно все 64 поля по одному разу и вернуться в исходное поле?
Несмотря на внешнее сходство задач об эйлеровых и гамильтоновых циклах, оказалось, что эффективных критериев существования гамильтоновых циклов ( в отличии от эйлеровых) не существует.
3.7. Деревья и леса
Связный граф без циклов называется деревом.
Граф без циклов называется лесом.
Теорема. T(V,E) - дерево тогда и только тогда, когда T(V,E) - связный граф и |E|=|V| - 1.
Теорема. В любом дереве имеется не менее двух висячих вершин.
3.8. Цикломатическое число графа. Построение остовного дерева связного графа.
Остовным деревом связного графа G(V,E) называется любой его подграф, содержащий все вершины G и являющийся деревом.
На рисунке приведены два графа G и по одному из их остовных деревьев T.
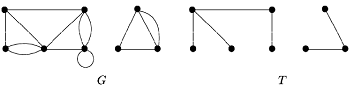
Число ребер, которое необходимо удалить для получения остова, называется цикломатическим числом графа G и обозначается 
.
Теорема. Цикломатическое числом графа G(V,E) не зависит от последовательности удаления ребер и имеет место формула:
= |E|| - |V|+k(G),
где k(G) - число компонент связности.