6.1.1. Антиподные и ортогональные сигналы
6.1.2. М-арная передача сигналов
Тему канального кодирования можно условно разделить на два раздела: кодирование (или обработка) сигнала и структурированные последовательности (или структурированная избыточность), как это показано на рис. 6.1. Кодирование сигнала означает преобразование сигнала в некий "улучшенный сигнал", позволяющий сделать процесс, обнаружения менее подверженным ошибкам. Метод структурированных последовательностей — это преобразование последовательности данных в новую, "улучшенную последовательность", обладающую структурной избыточностью (которая вмешает избыточные биты). Эти избыточные разряды служат для определения и исправления ошибок. На выходе процедуры кодирования получается закодированный (формой сигнала или структурированной последовательностью) сигнал, имеющий лучшие пространственные характеристики, чем некодированный. Итак, сначала рассмотрим некоторые методы кодирования сигнала, а затем, начиная с раздела 6.3, обсудим суть структурированных последовательностей.
6.1.1. Антиподные и ортогональные сигналы
Антиподные и ортогональные сигналы уже обсуждались ранее, поэтому мы лишь напомним их основные особенности. В примере, приведенном на рис. 6.2, показано аналитическое представление набора синусоидальных антиподных сигналов (
), а также его векторное и графическое представление. Какие существуют альтернативные определения антиподных сигналов? О таких сигналах можно сказать, что они либо являются зеркальными отображениями друг друга, либо один сигнал является отрицательным по отношению к другому, либо они различаются между собой на 180°.
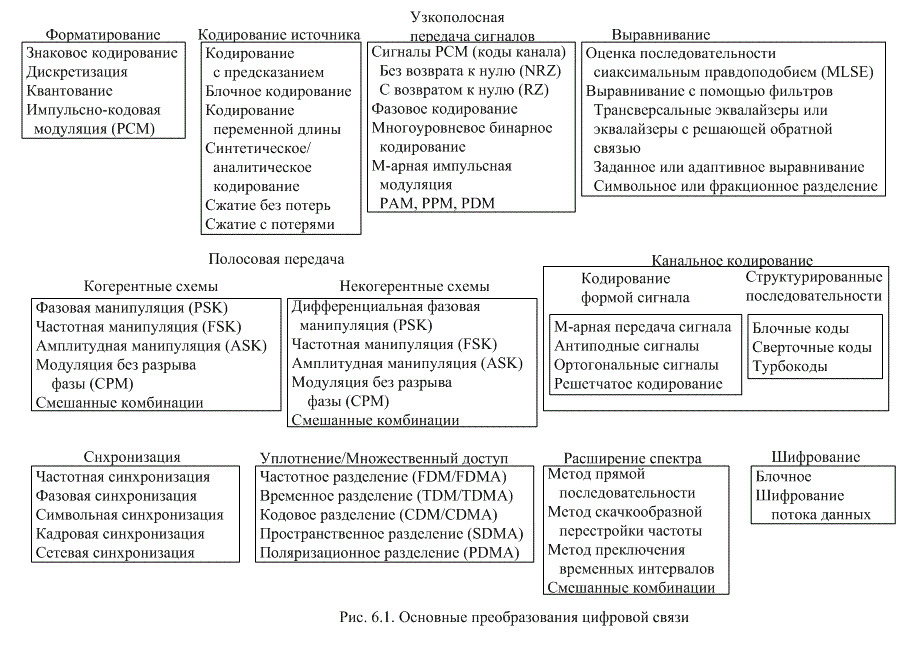
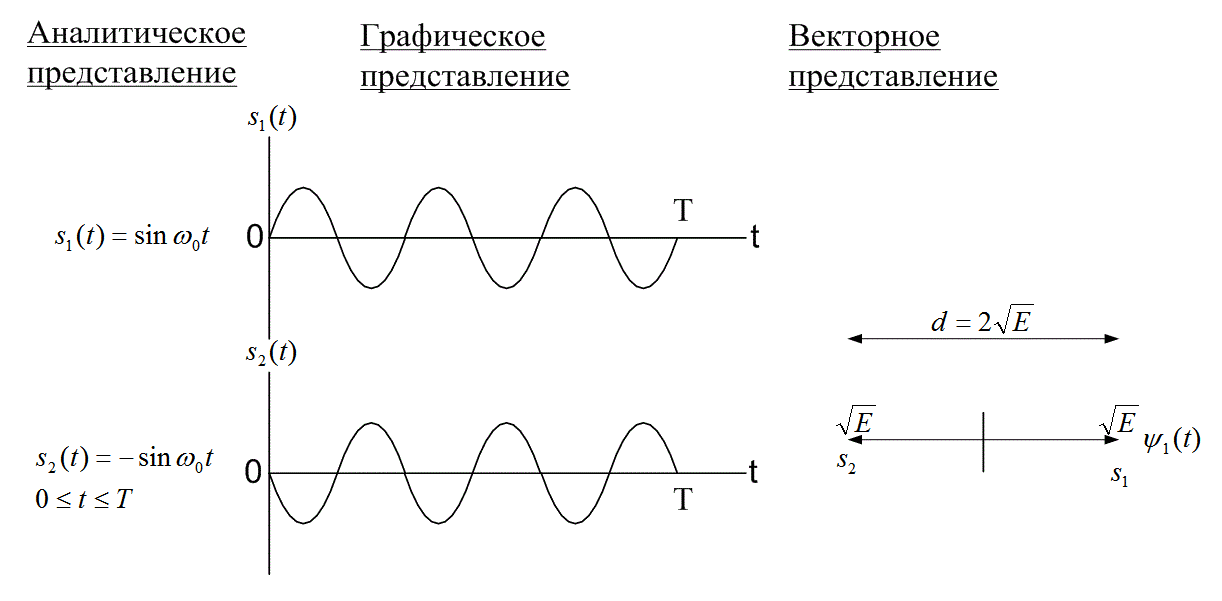
Рис. 6.2. Пример антиподного набора сигналов
В примере, приведенном рис. 6.3, показан набор ортогональных сигналов, которые имеют вид импульсов описывающихся следующими выражениями.
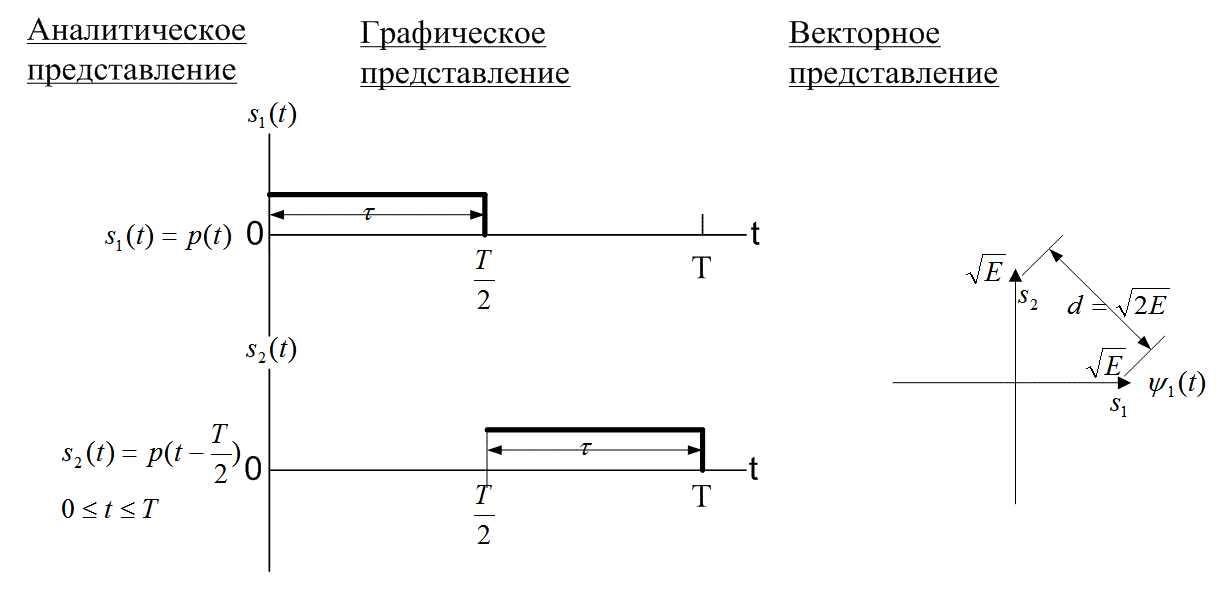
Рис. 6.3. Пример двоичного набора ортогональных сигналов
В данном случае p(t) — импульс длительностью 
, где Т— период. В системах связи .возможны и другое наборы ортогональных сигналов, например часто используемые sin x и cos x Любой набор равноэнергетических сигналов si(t), i = l,2,...,M, будет ортонормированным (ортогональным и нормированным на 1),тогда и только тогда, когда
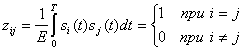(6.1)
где zij является коэффициентом взаимной корреляции (cross-correlation coefficient), а величина Е — энергией сигнала, выражаемой следующим образом.
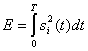(6.2)
Из графического представления на рис. 6.3 видно, что s1(t) и s2(t) не могут взаимодействовать, поскольку они разнесены во времени. Векторное представление показывает, что ортогональные сигналы перпендикулярны. Посмотрим на другие, альтернативные определения ортогональных сигналов или, векторов. Можно сказать, например, что скалярное произведение двух разных векторов в ортогональном наборе должно быть равно нулю. В двух- и трехмерных декартовых системах координат векторы сигналов можно представить геометрически, как взаимно ортогональные друг к другу. Можно также сказать, что один вектор имеет нулевую проекцию на другой или один сигнал не может взаимодействовать с другим, поскольку они"не принадлежат одному и тому же пространству сигналов.
6.1.2. M-арная передача сигналов
При M-арной передаче сигналов процессор за один такт работы принимает k бит данных. После этого он указывает модулятору произвести один из M = 2k сигналов; частным случаем k = 1 является двоичная передача сигнала. Для k > 1 М-арную передачу сигналов можно рассматривать как процедуру кодирования формы сигнала. При ортогональной передаче сигналов (например, сигналов MFSK) увеличение k приводит к повышению достоверности передачи или уменьшению требуемого Eb/NQ за счет увеличения полосы пропускания; при неортогональной передаче сигналов (например, сигналов MPSK) улучшение эффективности использования полосы пропускания происходит за счет снижения достоверности передачи или возрастания требуемого Eb/NQ. Подходящий выбор формы сигнала позволяет найти компромисс между вероятностью ошибки, Eb/NQ и эффективностью использования полосы пропускания. Более подробно такие компромиссы рассмотрены в главе 9.
6.1.3. Кодирование сигнала
Процедура кодирования сигнала состоит в преобразовании набора сигналов (представляющих набор сообщений) в усовершенствованный набор сигналов. Этот улучшенный набор можно использовать для получения более приемлемой величины РВ, соответствующей исходному набору. Наиболее популярные из таких кодов сигнала называются ортогональными (orthogonal) и биортогональными кодами (biorthogonal). В процессе кодирования каждый сигнал набора пытаются сделать настолько непохожим на другие, насколько это возможно, чтобы для всех пар сигналов коэффициент взаимной корреляции zij (см. уравнение 6.1) имел наименьшее возможное значение. Строго это условие выполняется тогда, когда сигналы антикоррелируют (zij = -1); этого можно добиться только в том случае, если в наборе всего два значения (М =2) и они антиподны друг другу. Вообще, все коэффициенты взаимной корреляции можно сделать равными нулю [1]. В этом случае набор будет ортогональным. Наборы антиподных сигналов являются оптимальными в том смысле, что все сигналы максимально удалены друг от друга, как можно видеть на рис. 6.2. Расстояние d между векторами сигналов определяется как 
, где Е— энергий сигнала на интервале T, как показано а уравнении (6.2). Сравнив пространственные характеристики ортогональных сигналов с характеристиками антиподных сигналов, приходим к выводу, что о первых можно сказать нечто вроде "довольно хорошо" (при данном уровне энергии сигнала). На рис. 6.3 расстояние между векторами ортогональных сигналов составляет 
Взаимная корреляция между двумя сигналами является мерой расстояния между двумя векторами сигналов. Чем меньше взаимная корреляция, тем больше векторы удалены друг от друга. Это можно проверить с помощью рис. 6.2, где антиподные сигналы (для которых zij =-l) представлены векторами, наиболее удаленными друг от друга, и рис. 6.3, где ортогональные сигналы (для которых zij = 0) представлены векторами, расположенными ближе друг к другу, чем антиподные векторы. Очевидно, что расстояние между идентичными сигналами (zij = 1) должно быть равно нулю.
Условие ортогональности в уравнении 6.1 записано через сигналы si(t) и sj(t), где i,j = 1, 2, ...,М (М — количество сигналов в наборе). Каждый сигнал набора 
может содержать последовательность импульсов с уровнями +1 или -1, которые представляют двоичную 1 или 0. Если выразить набор в таком виде, уравнение (6.1) можно упростить, положив, что состоит из ортогональных сигналов тогда и только тогда, когда
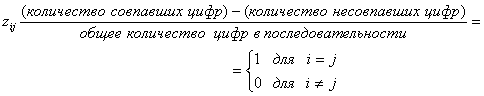(6.3)
6.1.3.1. Ортогональные коды
Набор однобитовых данных можно преобразовать с помощью ортогональных кодовых слов, состоящих из двух разрядов каждое, которые описываются строками показанной ниже матрицы Н1.
Набор данных Набор ортогональных кодовых слов
(6.4,а)
В этом и следующих примерах проверка ортогональности набора кодовых слов производится с помощью уравнения (6.3). Для кодирования набора двухбитовых данных упомянутый выше набор следует расширить по горизонтали и вертикали, что дает матрицу Н2.
Набор данных Набор ортогональных кодовых слов
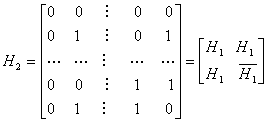(6.4,б)
Правый нижний квадрант является дополнением к исходному набору кодовых слов. С помощью подобной процедуры можно определить и ортогональный набор Н3для набора 3-битовых данных.
Набор данных Набор ортогональных кодовых слов
(6.4,в)
Вообще, для набора k-битовых данных из матрицы Hk-1, можно построить набор кодовых слов Hk размерностью 2k х 2k, который называется матрицей Адамара (Hadamard matrix).
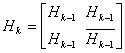(6.4,г)
Каждая пара слов в каждом наборе кодовых слов H1, H2, H3, …, Hk, … содержит одинаковое количество совпадающих и несовпадающих разрядов [2]. Поэтому, в соответствии с уравнением (6.3), zij = 0 (при 
) и каждый из этих наборов ортогонален.
Точно так же, как М-арная передача сигналов с ортогональной модуляцией (такой, как MFSK) понижает РB, кодирование информации ортогональным набором сигналов при когерентном обнаружении дает абсолютно такой же результат. Для одинаковых, равноэнергетических ортогональных сигналов вероятность ошибки в кодовом слове (символе), РЕ, можно оценить сверху, как [2]
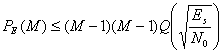, (6.5)
где размер набора кодовых слов М равен 2k, a k — это число информационных бит в кодовом слове. Функция Q(x) определена в уравнении (3.43), Es=kEb является энергией кодового слова. При фиксированном М с ростом Eb/N0 оценка становится все более точной; уже для РE(М)
10-3 уравнение (6.5) является довольно хорошим приближением. Для выражения вероятности появления ошибочного бита мы будем использовать связь между рв и РЕ, которая дается уравнением (4.112). Приведем ее повторно.
(6.6)
В результате объединения уравнений (6.5) и (6.6) вероятность появления ошибочного бита можно оценить следующим образом.
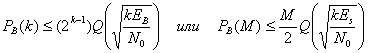(6.7)
6.1.3.2. Биортогональные коды
Биортогональный набор сигналов, состоящий из М сигналов или кодовых слов, получается из ортогонального набора, состоящего из M/2 сигналов, путем дополнения последнего сопряженными значениями каждого сигнала.
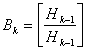
Например, набор 3-битовых данных можно преобразовать в биортогональный набор кодовых слов следующим образом.
Набор данных Набор ортогональных кодовых слов
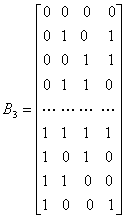
В действительности биортогональный набор состоит из двух ортогональных кодов, таких, что для каждого кодового слова в одном наборе имеется 'антиподное ему слово в другом. Биортогональный набор состоит из комбинации ортогональных и антиподных сигналов. Если использовать коэффициенты zij, введенные в уравнении (6.1), то биортогональные коды можно представить следующим образом.
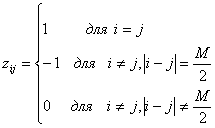(6.8)
Одно из преимуществ биортогональных кодов перед ортогональными заключается в том, что при передаче аналогичной информации размер кодового слова биортогональных кодов вдвое меньше размера кодового слова ортогональных кодов (сравните строки матрицы В3со строками представленной ранее матрицы Н3). Следовательно, при использовании биортогональных кодов требования к полосе пропускания вдвое слабее, чем при использовании ортогональных кодов. Поскольку антиподные векторы сигналов имеют лучшие пространственные характеристики, чем ортогональные, не должно удивлять, что биортогональные коды лучше ортогональных. Для одинаковых, равноэнергетических биортогональных сигналов вероятность ошибки в кодовом слове (символе) можно оценить [2] следующим образом.
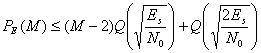(6.9)
При фиксированном М с ростом En/N0 оценка становится все более точной. Зависимость РB(М) от PE(м) является довольно сложной, но ее, согласно [2], можно аппроксимировать следующим образом.
Это приближение становится достаточно хорошим при M>8. Таким образом, Можно записать следующее.
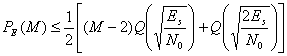(6.10)
Описанные биортогональные коды значительно снижают РB по сравнению с ортогональными кодами и требуют только вдвое меньшей полосы пропускания, чем аналогичные ортогональные коды.
6.1.3.3. Трансортогональные (симплексные) коды
Код, получаемый из ортогонального путем удаления первого разряда каждого кодового слова, называется трансортогональным (transorthogonal), или симплексным (simplex) кодом. Такой код описывается следующими значениями zij.
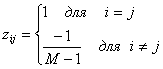(6.11)
С точки зрения минимальной энергии, необходимой для поддержания заданной вероятности ошибки, симплексный код эквивалентен равновероятному ортогональному набору. Сравнивая достоверность передачи ортогонального, биортогонального и симплексного кодов, можно сказать, что симплексный код имеет наименьшее требуемое Eb/N0 для получения определенной частоты появления символьных ошибок. Впрочем, при больших М все три схемы очень похожи между собой в смысле достоверности передачи. При этом биортогональное кодирование, по сравнению с другими методами, требует лишь половины полосы пропускания. В то же время для каждого из этих кодов требования к полосе пропускания (и сложность системы) экспоненциально растут с увеличением М; так что подобные схемы кодирования годятся лишь тогда, когда доступна значительная полоса пропускания.
6.1.4. Примеры системы кодирования сигналов
На рис. 6.4 дается пример присвоения k-битовому сообщению из набора размером M = 2k кодированной последовательности импульсов из кодового набора аналогичного размера. Каждое из k-битовых сообщений выбирает один генератор, производящий кодированную последовательность или кодовое слово. Последовательности в кодированном наборе, заменяющие исходные сообщения, формируют набор сигналов с хорошими Пространственными характеристиками (например, ортогональный, биортогональный). Для ортогонального кода, описанного в разделе 6.1.3.1, каждое кодовое слово состоит из М = 2k импульсов (представляющих кодовые биты). Таким образом, 2k кодовых бит заменяют k информационных бит. Затем выбранная последовательность с использованием двоичной PSK модулируется несущей волной, так что фаза (φj = 0 или я) несущей волны в течение каждого интервала передачи кодированного бита, 
.соответствует амплитуде (j=-1 или 1) j-го биполярного импульса в кодовом слове. В приемнике, показанном на рис. 6.5, сигнал демодулируется и подается на М корреляторов (или согласованных фильтров). Для ортогональных кодов, таких как описаны в разделе 6.1.3.1 (которые определяются матрицей Ада-мара), за период передачи кодового слова (
) определяются корреляции принятого сигнала. Для систем связи реального времени сообщения не могут опаздывать, поэтому время передачи кодового слова должно совпадать е длительностью сообщения. Следовательно, T также можно выразить как 
, где Тb — длительность битов сообщения. Отметим, что длительность бита сообщения в M/k раз больше, чем у кодового бита. Другими словами, кодовые биты или кодированные импульсы (сигналы PSK) должны перемещаться со скоростью, в M/k раз большей, чем биты сообщения. Для ортогонально кодированных сигналов и каналов с шумом AWGN математическое ожидание выходной мощности для каждого коррелятора в момент времени Т равно нулю; исключением является только коррелятор, соответствующий переданному кодовому слову.
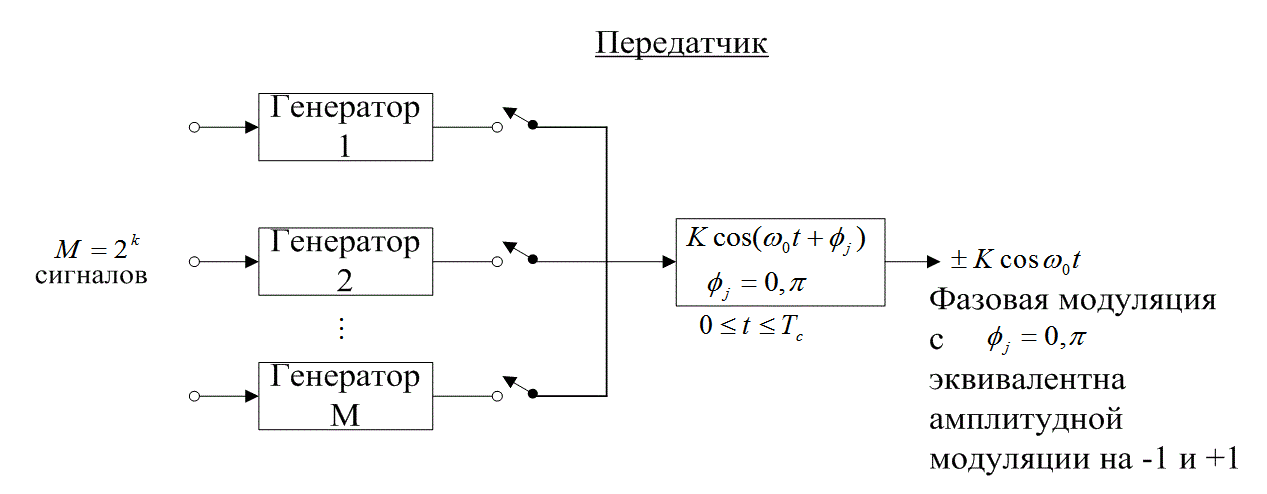
Рис. 6.4. Система кодирования сигналов (передатчик)
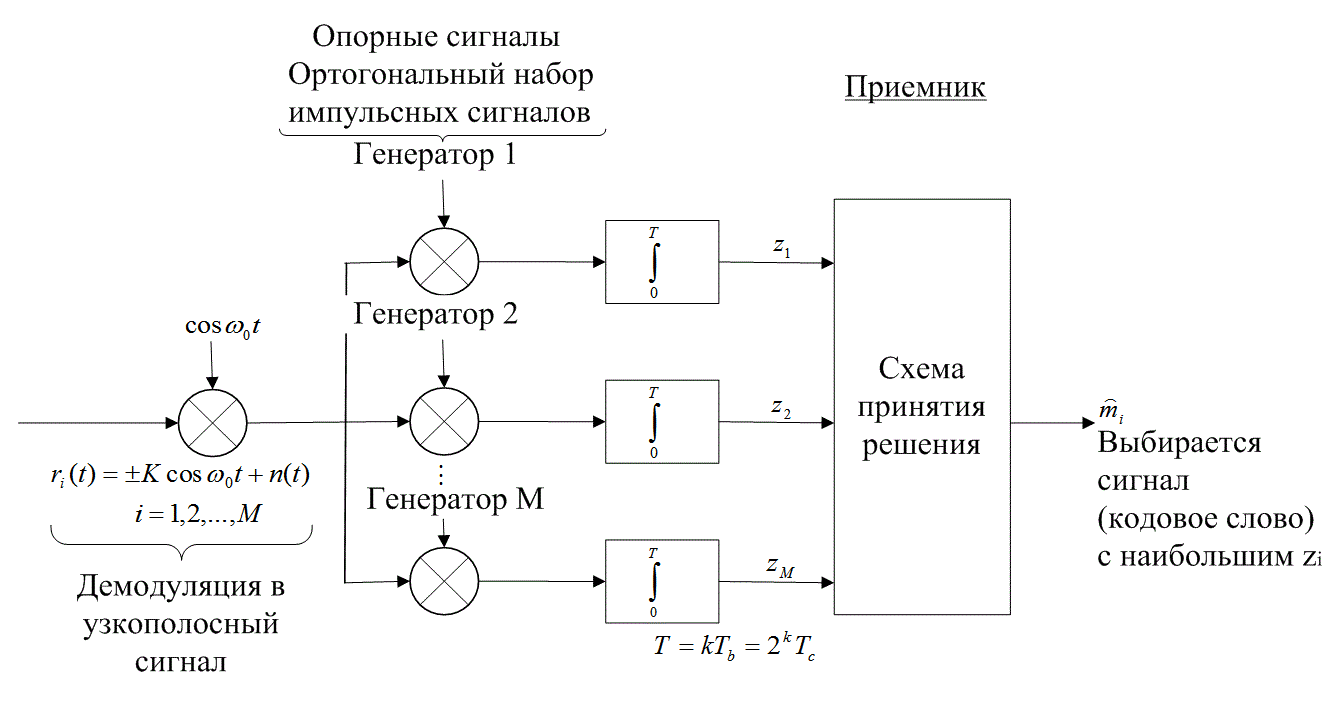
Рис. 6.5. Система кодирования сигналов с когерентным обнаружением (приемник)
Каковы преимущества описанного ортогонального кодирования сигналов по сравнению с обычным поступлением в каждую единицу времени одного бита или одного импульса? Можно оценить достоверность передачи с таким кодированием и без него, сравнив уравнение (4.79) для когерентного обнаружения антиподных сигналов с уравнением (6.7) для когерентного обнаружения ортогональных кодовых слов. При данном размере k-битового сообщения (скажем, k = 5) и желаемой вероятности появления ошибочного бита (например, 10-5), обнаружение ортогональных кодовых слов (каждое из которых состоит из 5 бит) может выполняться с приблизительно на 2,9 дБ меньшим отношением Eb/N0, чем побитовое обнаружение антиподных сигналов. (Проверить этот факт предоставляется читателю в качестве задачи 6.28.) Данный результат можно было предвидеть, сравнив рабочие характеристики ортогональной передачи сигналов на рис. 4.28 с характеристиками бинарной (антиподной) передачи на рис. 4.29. Чем мы платим за такой уровень достоверности передачи? Плата выражается в увеличении полосы пропускания. В приведенном примере передача некодированного сообщения — это посылка 5 бит. Сколько кодированных импульсов необходимо отправить для передачи с кодированием каждой последовательности сообщения? В данном примере каждая 5-битовая последовательность сообщения представлена М = 2k = 25 = 32 кодовыми битами или кодированными импульсами. 32 кодированных импульса, составляющих кодовое слово, нужно отправить за то же время, что и соответствующие исходные 5 бит. Таким образом, требуемая ширина полосы пропускания составляет 32/5 от ширины полосы пропускания в случае без кодирования. Вообще, полоса пропускания, необходимая для подобных ортогонально кодированных сигналов, в M/k раз больше требуемой в случае передачи без кодирования. Далее мы рассмотрим более выгодные и эффективные способы получения компромиссов между шириной полосы пропускания и схемой кодирования [3, 4].