Основной задачей анализа является определение реакции (выходного) сигнала цепи при действии на её входе сигнала известной формы. При этом, входной сигнал может быть описан как во временной, так и в частотной области. В связи с этим различают следующие методы анализа: классический, временной (или метод интеграла наложения), спектральный и операторный. Выбор того или иного метода зависит от структуры цепи, вида воздействующего на неё сигнала, формы представления (временная или частотная) входного сигнала.
5.4.1. Классический метод
Классический метод основывается на решении дифференциального уравнения вида (5.16), описывающего линейную цепь. Решение этого уравнения представляет собой сумму двух слагаемых
, (5.19)
где первое слагаемое представляет собой общее решение однородного дифференциального уравнения
, (5.20)
а второе слагаемое – частотное решение (5.16) при 
, где 
– правая часть уравнения (5.16). Физически 
– свободная составляющая полного отклика (выходного сигнала), представляет собой реакцию цепи на отключение(или включение) входного сигнала и характеризует переходные процессы в цепи. Второе слагаемое 
– вынужденная составляющая, является реакцией цепи после окончания переходных процессов и характеризует установившейся(стационарный) режим преобразования цепью входного сигнала. Обычно, классический метод используется для изучения переходных процессов, что приводит к необходимости решения уравнения (5.20). Общее решение однородного уравнения (5.20) имеет вид
, (5.21)
где 
, 
,…, 
– постоянные коэффициенты, определяемые начальными условиями,
, 
,…, 
– корни характеристического уравнения:
. (5.22)
Это уравнение имеет ровно n корней, при этом корни могут быть либо вещественными, либо комплексными, что определяет характер переходных процессов. Что же касается 
, то если входной сигнал является постоянным или периодическим, то после окончания переходных процессов выходной сигнал принимает форму входного сигнала. Так, если 
представляет собой гармонический сигнал, то также будет гармоническим, отличаясь от входного сигнала амплитудой и начальной фазой.
В качестве примера рассмотрим, что собой представляет отклик RC-цепи (рис. 5.3,8) на входной сигнал вида 
.
Дифференциальное уравнение цепи (5.15) перепишем в виде
,
где 
– постоянная времени.
Поскольку дифференциальное уравнение имеет порядок n=1, решение однородного уравнения
согласно (5.21), запишется в виде
,
где 
– корень характеристического уравнения
,
откуда следует 
. Тогда
.
До поступления входного сигнала ёмкость С разряжена. В момент 
поступления входного сигнала (скачка) ёмкость не может мгновенно зарядиться до 
, это произойдёт по мере перехода к установившемуся режиму. Очевидно в установившемся режиме
.
Таким образом, суммарный выходной сигнал
.
Коэффициент 
найдём из начальных условий. Начальными условиями при исследовании линейных цепей называют значения токов в индуктивностях и напряжений на емкостях в момент времени . Так как в этот момент времени 
, то можно записать
,
Откуда следует 
. Тогда окончательно суммарный выходной сигнал
.
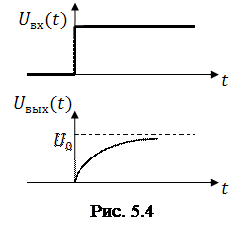
На рис. 5.4. изображены эпюры напряжений на входе и выходе исследуемой RC-цепи.
5.4.2. Временной метод
Временной метод (метод интеграла положения, метод интеграла Дюамеля) основывается на представлении входного сигнала цепи в виде суммы элементарных сигналов вида единичного скачка или очень короткого импульса ( 
– функции). Тогда, зная отклик линейной цепи на каждый элементарный сигнал и суммируя их можно получить в соответствии с принципом суперпозиции (наложения) полный отклик цепи на входной сигнал сложной формы.
Выберем в качестве элементарного сигнала – функцию. Тогда входной сигнал в соответствии с (1.19) можно записать следующим образом
.
Очевидно, выходной сигнал
.
Так как оператор 
не зависит от времени, его можно внести под знак интеграла. Тогда, с учётом (5.5)
. (5.23)
Если момент появления входного сигнала 
, то с учётом того, что выходной сигнал не может появиться ранее входного, выражение (5.23) принимает вид
. (5.24)
Таким образом, сигнал на выходе линейной цепи представляет собой свёртку входного сигнала с импульсной характеристикой цепи. Линейная цепь с постоянными параметрами при преобразовании проводит операцию взвешенного суммирования всех мгновенных значений входного сигнала, начиная с момента и заканчивая текущим моментом времени 
. Роль весовой функции выполняет импульсная характеристика цепи.
Выражение (5.24) носит название интеграла Дюамеля. Это выражение было получено в предположении, что входной сигнал представлен в виде суммы элементарных сигналов вида – функций. Если входной сигнал представить в виде (1.15) комбинаций сигналов вида единичного скачка, то можно получить другие формы интеграла Дюамеля, в частности
. (5.25)
Здесь 
– переходная характеристика цепи.
Итак, для использования метода интеграла наложения необходимо знать импульсную характеристику 
или переходную характеристику 
. Эти характеристики можно определить несколькими способами. Прямой (непосредственный способ состоит в решении дифференциального уравнения (5.20) в предположении, что входной сигнал является очень коротким импульсом(для определения импульсной характеристики) или сигналом вида единичного скачка( для определения переходной характеристики).
В выше приведённом примере было решено дифференциальное уравнение и найден отклик RC-цепи на воздействие сигнала
.
Очевидно, форма отклика не изменится, если входной сигнал будет единичным скачком, при этом масштаб отклика изменится в 
раз. Тогда выходной сигнал
, (5.26)
поскольку реакция цепи на единичный скачок является переходной характеристикой. В соответствии с (5.7) определяется импульсная характеристика
(5.27)
Второй способ определения импульсной или переходной характеристики, назовём его косвенным, состоит в использовании однозначного соответствия между импульсной характеристикой и комплексным коэффициентом передачи.
5.4.3. Спектральный метод
При рассмотрении характеристик линейной цепи было получено соотношение (5.10), связывающее спектральные характеристики входного и выходного сигнала с комплексным коэффициентом передачи цепи. Это соотношение лежит в основе спектрального анализа. Если задачей анализа является определение частотных характеристик выходного сигнала, то при известных 
и 
использование (5.10) полностью решает эту задачу. В ряде случаев сигнал представлен во временной области и требует найти отклик цепи как функцию времени. При этом использование метода интеграла наложения может быть затруднено сложностью нахождения импульсной характеристики цепи. В то же время комплексный коэффициент передачи найти достаточно просто. Тогда спектральный метод анализа сводится к следующим операциям:
- для входного сигнала прямым преобразованием Фурье находится комплексный спектр ;
- определяется комплексный коэффициент передачи цепи ;
- в соответствии с (5.10) определяется комплексный спектр выходного сигнала 
;
- обратным преобразованием Фурье вычисляется форма сигнала 
на выходе цепи.
Итак, важнейшим условием использования спектрального метода является знание комплексного коэффициента передачи исследуемой цепи. Найти комплексный коэффициент передачи можно, используя методы теории цепей (метод узловых потенциалов или метод контурных токов). Если известно аналитическое описание цепи дифференциальным уравнением (5.16), то комплексный коэффициент передачи находится в соответствии с (5.18). Наконец, цепь можно представить в виде делителя напряжения, элементами которого являются комплексные сопротивления
; 
; 
.
Проиллюстрируем последний подход на примере уже рассматривавшейся выше RC-цепи. Если представить цепь как делитель напряжения, то выходной сигнал представляет собой напряжение на ёмкости С. Тогда, если 
комплексный ток, протекающий в цепи, то
,
и комплексный коэффициент передачи
,
что совпадает с результатом, полученным в подразделе 5.3.
5.4.4. Операторный метод
Операторный метод является обобщением спектрального метода. В основе метода лежит преобразование Лапласа. Рассмотрим некоторый сигнал 
, определённый на интервале времени (0, 
). Умножим этот сигнал на 
и полученный новый сигнал 
подвергнем преобразованию Фурье
.
Обозначая через 
, получим
. (5.28)
Выражение (5.28) называется односторонним преобразованием Лапласа функции . При этом, называют оригиналом, а 
изображением.
Нетрудно убедиться, что при 
выражение (5.28) преобразуется к виду
,
что соответствует преобразованию Фурье. Таким образом если преобразование Фурье представляет собой спектральное разложение сигнала по гармоническим составляющим 
, то преобразование Лапласа – разложение сигнала по экспоненциально – косинусным составляющим 
. Действительно, представим
.
Здесь использована формула Эйлера
.
С другой стороны
,
где 
.
Тогда окончательно
представляет собой экспоненциально – косинусную функцию.
Переход от изображения 
к оригиналу осуществляется при помощи обратного преобразования Лапласа
. (5.29)
Для значительной части функций широко используемых при описании оригиналов были рассчитаны изображения по Лапласу. Некоторая часть оригиналов и изображений приведена в таблице 5.1.
Поскольку преобразование Лапласа является обобщением преобразования Фурье, то оно обладает теми же свойствами, что и преобразование Фурье. Остановимся на некоторых из них, которые будем использовать в дальнейшем. Пару преобразований (прямое и обратное) будем обозначать следующим образом
.
1. Линейность преобразований Лапласа
(5.30)
2. Свойство временного сдвига
(5.31)
3. Операция дифференцирования
; 
(5.32)
4. Операция интегрирования
. (5.33)
Применим к обеим частям уравнения (5.16) прямое преобразования Лапласа. Тогда с учётом (5.32), получим
(5.34)
откуда следует
. (5.35)
Это отношение называется передаточной функцией цепи или её операторным коэффициентом. Таким образом, передаточная функция является оператором преобразования линейной цепью в базисе экспоненциально – косинусных сигналов.
Сравним выражение комплексного коэффициента передачи (5.18) с выражением (5.35). Из этого сравнения следует, что комплексный коэффициент передачи является частным случаем 
при , т.е.
(5.36)
Таким образом, если известна передаточная функция цепи, то операторный метод поиска отклика цепи состоит в следующем:
- находится изображение по Лапласу входного сигнала
; (5.37)
- находится изображение выходного сигнала как произведение
; (5.38)
- определяется оригинал выходного сигнала
. (5.39)
Установим связь между временными характеристиками и передаточной функцией. Произведя в (5.12) замену 
на 
, получим
.
Таким образом, передаточная функция и импульсная характеристика связаны между собой преобразованием Лапласа
.
Что касается переходной характеристики, то применяя к (5.8) преобразование Лапласа и учитывая (5.33), получим
.
В заключение отметим, что операторный метод позволяет сводить линейные дифференциальные уравнения вида (5.16) к алгебраическим уравнениям (5.34), что позволяет в ряде случаев упростить анализ цепей. Помимо этого, учитывая широкое распространение таблиц преобразований Лапласа для большого числа функций, можно исключить громоздкие вычисления, непосредственно обращаясь к этим таблицам.
Рассмотрим применение операторного метода на примере анализа определения отклика RC-цепи на входной сигнал вида . Эта задача была решена классическими временными методами. Спектральным методом был найден комплексным коэффициент передачи. Заменив в выражении для цепи на , получим передаточную функцию цепи
.
Следуя операторному методу найдём изображение по Лапласу входного сигнала, воспользовавшись при этом таблицей 5.1
.
Далее, в соответствии с (5.38), определим изображение выходного сигнала
.
И наконец, по таблице 5.1 (позиция 5) находим оригинал
,
что совпадает с полученными ранее результатами.