13.2. Квантование амплитуды

Категория: 13. Кодирование источника

13.2.1. Шум квантования

13.2.2. Равномерное квантование

13.2.2.1. Сигнал и шум квантования в частотной области

13.2.3. Насыщение

13.2.4. Добавление псевдослучайного шума

13.2.5. Неравномерное квантование

13.2.5.1. Субоптимальное неравномерное квантование

13.2.5.2. Логарифмическое сжатие

Квантование амплитуды — это задача отображения выборок волновых сигналов непрерывной амплитуды в конечное множество амплитуд. Аппаратное обеспечение, которое выполняет отображение, — это аналогоцифровой преобразователь (analog-to-digital converter — ADC, АЦП). Квантование амплитуды происходит после операции выборки-запоминания. Простейшее устройство квантования, которое можно изобразить, выполняет мгновенное отображение с каждого непрерывного входного выборочного уровня в один из предопределенных, равномерно расположенных выходных уровней. Квантующие устройства, которые характеризуются равномерно расположенными приращениями между возможными выходными уровнями, называются равномерными устройствами квантования, или линейными квантующими устройствами. Возможные мгновенные характеристики входа/выхода легко изображаются с помощью простого ступенчатого графика, подобного изображенному на рис. 13.3. На рис. 13.3, а, б и г представлены устройства с равномерными шагами квантования, а на рис. 13.3, в — устройство с неравномерным шагом квантования. На рис. 13.3, а характеристика устройства имеет нуль в центре шага квантования, а на рис. 13.3, б и г — на границе шага квантования. Отличительная особенность устройств, имеющих характеристики с нулем в центре шага квантования и характеристики с нулем на границе шага квантования, связана, соответственно, с наличием или отсутствием выходных изменений уровня, если входом квантующего устройства является шум низкого уровня. На рис. 13.3, г представлено смещенное (т.е. усекающее) устройство квантования, а другие устройства, изображенные на рисунке, являются несмещенными и называются округляющими. Такие несмещенные устройства квантования представляют собой идеальные модели, но в аналого-цифровых преобразователях округление не реализуется никогда. Как правило, устройства квантования реализуются как усекающие преобразователи. Термины "характеристика с нулем в центре шага квантования" (midtread) или "характеристика с нулем на границе шага квантования" (midriser) относятся к ступенчатым функциям и используются для описания того, имеются ли в начале координат горизонтальная или вертикальная составляющая ступенчатой функции. Пунктирная линия единичного наклона, проходящая через начало координат, представляет собой неквантованную характеристику входа/выхода, которую пытаются аппроксимировать ступенчатой функцией. Разность между ступенчатой функцией и отрезком линии единичного наклона представляет собой ошибку аппроксимации, допускаемую устройством квантования на каждом входном уровне. На рис. 13.4 показана ошибка аппроксимации амплитуды в сравнении с входной амплитудой функции для каждой из характеристик квантующего устройства, изображенных на рис. 13.3. Рис. 13.4 соответствует рис. 13.3. Часто эта ошибка моделируется как шум квантования, поскольку последовательность ошибок, полученная при преобразовании широкополосного случайного процесса, напоминает аддитивную последовательность шума. Однако, в отличие от действительно аддитивных источников шума, ошибки преобразования являются сигнально зависимыми и высоко структурированными. Желательно было бы нарушить эту структуру, что можно сделать путем введения независимых шумовых преобразований, известных как псевдослучайный шум, предшествующих шагу преобразования. (Эта тема обсуждается в разделе 13.2.4.)

Линейное устройство квантования легко реализовать и очень легко понять. Оно представляет собой универсальную форму квантующего устройства, поскольку не предполагает никаких знаний о статистике амплитуд и корреляционных свойствах входного волнового сигнала, а также не использует преимуществ требований к точности, предоставляемых пользователями. Устройства квантования, которые используют указанные преимущества, являются более эффективными как кодеры источника и предназначены для более специфических задач, чем общие линейные устройства квантования. Эти квантующие устройства являются более сложными и более дорогими, но они оправдывают себя с точки зрения улучшения производительности системы. Существуют приложения, для которых равномерные устройства квантования являются наиболее желаемыми преобразователями амплитуды. Это — приложения обработки сигналов, графические приложения, приложения отображения изображений и контроля процессов. Для некоторых иных приложений более приемлемыми преобразователями амплитуды являются неравномерные адаптивные квантующие устройства. Эти устройства включают в себя кодеры волнового сигнала для эффективного запоминания и эффективной связи, контурные кодеры для изображений, векторные кодеры для речи и аналитические/синтетические кодеры (такие, как вокодер) для речи.

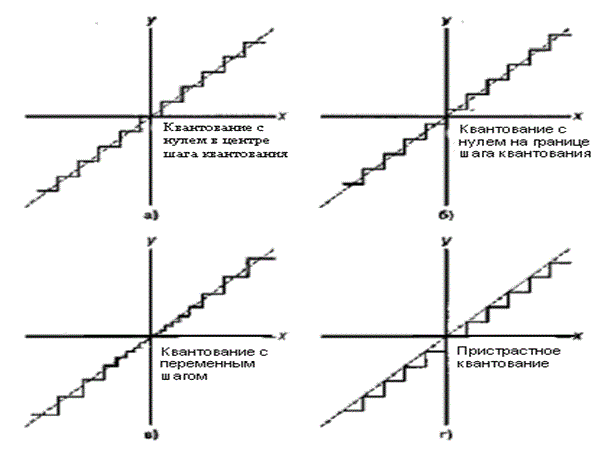Рис. 13.3. Различные передаточные функции устройства квантования

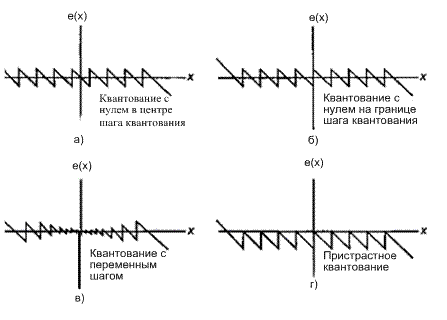
Рис. 13.4. Мгновенная ошибка для различных передаточных функций устройства квантования

13.2.1. Шум квантования

Разность между входом и выходом преобразователя называется ошибкой квантования (quantizing error). На рис. 13.5 изображен процесс отображения входной последовательности x(t) в квантованную выходную последовательность x(t). Получение x(t) можно представить как сложение каждого x(t) с ошибочной последовательностью e(i).

Ошибочная последовательность e(t) детерминированно определяется входной амплитудой через зависимость мгновенной ошибки от амплитудной характеристики, изображенной на рис. 13.4. Отметим, что ошибочная последовательность демонстрирует две различные характеристики в различных входных рабочих областях.

Первым рабочим интервалом является гранулированная область ошибок, соответствующая подаче на вход пилообразной характеристики ошибки. Внутри этого интервала квантующие устройства ограничены размерами соседних ступенчатых подъемов. Ошибки, которые случаются в этой области, называются гранулированными (granular errors), или иногда ошибками квантования (quantizing error). Входной интервал, для которого ошибки преобразования являются гранулированными, определяет динамическую область преобразователя. Этот интервал иногда называется областью линейного режима (region of linear operation). Соответствующее использование квантующего устройства требует, чтобы условия, порожденные входным сигналом, приводили динамическую область входного сигнала в соответствие с динамической областью устройства квантования. Этот процесс является функцией сигнально зависимой системы регулировки усиления, называемой автоматической регулировкой усиления (automatic gain control — AGC, АРУ), которая показана на пути прохождения сигнала на рис. 13.5.

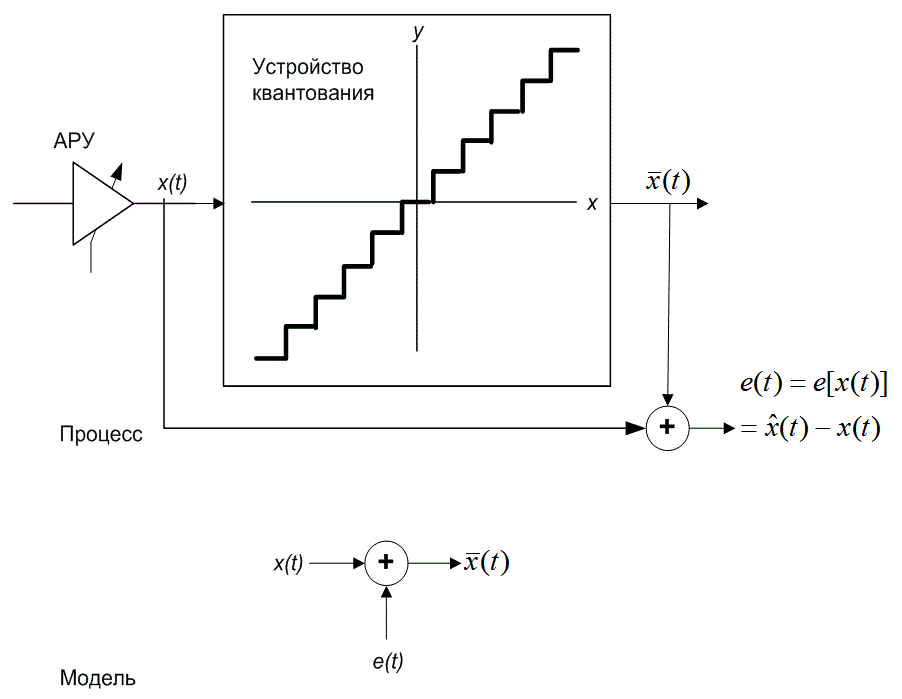
Рис. 13.5. Процесс и модель повреждения входного сигнала шумом квантования

Вторым рабочим интервалом является негранулированная область ошибок, соответствующая линейно возрастающей (или убывающей) характеристике ошибки. Ошибки, которые происходят в этом интервале, называются ошибками насыщения (saturation error) или перегрузки (overload error). Когда квантующее устройство работает в этой области, говорят, что преобразователь насыщен. Ошибки насыщения больше, чем гранулированные ошибки, и могут оказывать большее нежелательное влияние на точность воспроизведения информации.

Ошибка квантования, соответствующая каждому значению входной амплитуды, представляет слагаемое ошибки или шума, связанное с данной входной амплитудой. Если интервал квантования мал в сравнении с динамической областью входного сигнала и входной сигнал имеет гладкую функцию плотности вероятности в интервале квантования, можно предположить, что ошибки квантования равномерно распределены в этом интервале, как изображено на рис. 13.6. Функция плотности вероятности с нулевым средним соответствует округляющему квантующему устройству, в то время как функция плотности вероятности со средним -q/2 соответствует усекающему квантующему устройству.

Квантующее устройство, или аналого-цифровой преобразователь (analog-to-digital converter — ADC, АЦП), определяется числом, размером и расположением своих уровней квантования (или границами шагов и соответствующими размерами шагов). В равномерном квантующем устройстве размеры шагов равны и расположены на одинаковом расстоянии. Число уровней N обычно является степенью 2 вида N = 2b, где b — число бит, используемых в процессе преобразования.

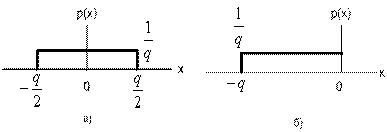
Рис. 13.6. Функции плотности вероятности для ошибки квантования, равномерно распределенной в интервале квантили, q: а) функция плотности вероятности для округляющего преобразователя; б) функция плотности вероятности для усекающего преобразователя

Это число уровней равномерно распределено в динамической области возможных входных уровней. Обычно этот интервал определяется как +Emax, подобно ±1,0 В или ±5,0 В. Таким образом, для полного интервала 2Emax величину шага преобразования получим в следующем виде.

(13.11)

В качестве примера использования равенства (13.11) шаг квантования (в дальнейшем называемый квантилъю) для 10-битового преобразователя, работающего в области ±1,0V, равен 1,953 мВ. Иногда рабочая область преобразователя изменяется так, что квантиль является "целым" числом. Например, изменение рабочей области преобразователя до ±1,024 В приводит к шагу квантования, равному 2,0 мВ. Полезным параметром равномерного квантующего устройства является его выходная дисперсия. Если предположить, что ошибка квантования равномерно распределена в отдельном интервале ширины q, дисперсия квантующего устройства (которая представляет собой шум квантующего устройства или мощность ошибки) для ошибки с нулевым средним находится следующим образом.

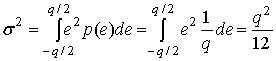(13.12)

где р(е) = l/q в интервале q — это функция плотности вероятности (probability density function — pdf) ошибки квантования е. Таким образом, среднеквадратическое значение шума квантования в интервале квантили ширины q равно или 0,29q. Уравнение (13.12) определяет мощность шума квантования в интервале размером в одну квантиль в предположении, что ошибки равновероятны в пределах интервала квантования. Если включить в рассмотрение работу в интервале насыщения квантующего устройства или рассмотреть неравномерные устройства квантования, то получим, что интервалы квантования не имеют равной ширины внутри области изменения входной переменной и плотность амплитуды не является равномерной внутри интервала квантования. Можно вычислить эту зависящую от амплитуды энергию ошибки усредняя квадраты ошибок по амплитуде переменной, взвешенной вероятностью этой амплитуды. Это можно выразить следующим образом.

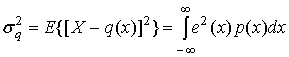(13.13)

где х — входная переменная, q(x) — ее квантованная версия, е(х) = х - q(x) — ошибка, а р(х) — функция плотности вероятности амплитуды х. Интервал интегрирования в формуле (13.13) можно разделить на два основных интервала: один отвечает за ошибки в ступенчатой или линейной области квантующего устройства, а второй — за ошибки в области насыщения. Определим амплитуду насыщения квантующего устройства как Emaх. Предположим также, что передаточная функция квантующего устройства есть четно-симметричной и такой же является функция плотности вероятности для входного сигнала. Мощность ошибки , определенная равенством (13.13), является полной мощностью ошибки, которая может быть разделена следующим образом.


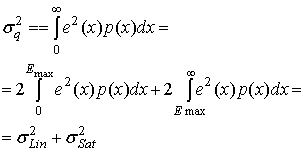
(13.14,а)

(13.14,6)

Здесь — мощность ошибки в линейной области, a — мощность ошибки в области насыщения. Мощность ошибки может быть далее разделена на подынтервалы, соответствующие последовательным дискретным входным уровням квантующего устройства (т.е. квантилям). Если предположить, что существует N таких уровней квантили, интеграл превращается в следующую сумму.

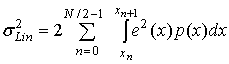(13.15)

где хn — уровень квантующего устройства, а интервал или шаг между двумя такими уровнями называется интервалом квантили (quantile interval). Напомним, что N, как правило, является степенью 2. Таким образом, существует N/2 — 1 положительных уровней, N/2 - 1 отрицательных уровней и нулевой уровень — всего N - 1 уровень и N -2 интервала. Теперь, если аппроксимировать плотность на каждом интервале квантили константами qn= (xn+1 - хn), выражение (13.15) упростится до следующего вида.

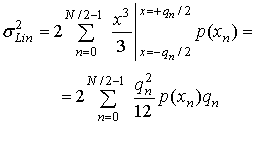(13.16)

где е(х) в равенстве (13.15) было заменено х из (13.16), поскольку е(х) — линейная функция от х, имеющая единичный наклон и проходящая через нуль в центре каждого интервала. Кроме того, пределы интегрирования в равенстве (13.15) были заменены в соответствии с изменениями х внутри интервала квантили. Поскольку область изменения была обозначена через qn, нижний и верхний пределы могут быть обозначены как х= -qn/2 и х= +qn/2. Равенство (13.16) описывает мощность ошибки в линейной области в виде суммы мощности ошибки q/12 в каждом интервале квантили, взвешенной вероятностью p(xn)qn этой энергии ошибки.

13.2.2. Равномерное квантование

Если устройство квантования имеет равномерно расположенные квантили, равные q, и все интервалы равновероятны, выражение (13.16) упрощается далее.

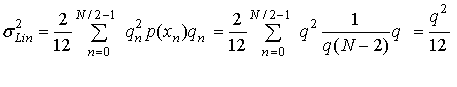(13.17)

Если квантующее устройство работает не в области насыщения (мощности шума квантования), тогда и эти величины часто используются как взаимозаменяемые. Отметим, что мощность шума сама по себе не будет полно описывать поведение шума устройства квантования. Более полной мерой качества является отношение второго центрального момента (дисперсии) шума квантования к входному сигналу. Если предположить, что входной сигнал имеет нулевое среднее, дисперсия сигнала равна следующему.

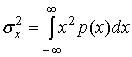(13.18)

Дальнейшее изучение среднего шума квантующего устройства требует конкретизации функции плотности и устройства.

Пример 13.4. Равномерное квантующее устройство

Определим дисперсию устройства квантования и отношение мощности шума к мощности сигнала (noise-to-signal power ratio — NSR) для равномерно распределенного в полной динамической области сигнала, созданного устройством квантования с 2b расположенными на одинаковых расстояниях уровнями квантили. В этом случае шума насыщения не существует и должна быть вычислена только величина линейного шума. Каждый интервал квантили равен следующему.

Здесь 2Еmax — это входной интервал между положительной и отрицательной границами линейной области квантования.

Решение

Подставляя выражение (13.19) в формулу (13.12) или (13.17), получим следующую мощность шума квантования (в линейной области).

Мощность входного сигнала находится посредством интегрирования выражения (13.18) j равномерной плотности вероятности в интервале длины с центром в точке 0, так р(х) = l/(), и дисперсия сигнала находится следующим образом.

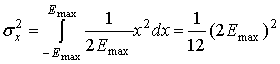
Рассматривая отношение мощности шума к мощности сигнала (NSR), получим следующё

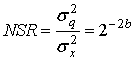
Теперь, превращая NSR в децибелы, получим следующее.

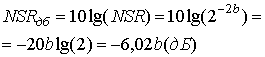
Выражение (13.23, б) свидетельствует о том, что за каждый бит, который используете процессе преобразования, мы платим -6,02 дБ отношения шума к сигналу. Действитель NSR для любого равномерного квантующего устройства, не работающего в области насьи ния, имеет следующий вид.

Здесь член С зависит от функции плотности вероятности сигнала (probability density fu tion — pdf); он положителен для функций плотности, являющихся узкими по отношени] уровню насыщения преобразователя.

13.2.2.1. Сигнал и шум квантования в частотной области

До настоящего момента шум квантования обсуждался с точки зрения его влиж на выборку временного ряда, представляющую дискретный сигнал. Шум квантования может быть также описан в частотной области; это позволяет взглянуть на влияние условий работы, что и будет сделано ниже. В процессе этого изучения предполагает также рассмотрение насыщения (раздел 13.2.3), возмущения (раздел 13.2.4) и квантующих устройств с обратной связью по шуму (раздел 13.2.6).

На рис. 13.7 представлено дискретное преобразование Фурье двух синусоид, которые были образованы линейным 10-битовым АЦП. Сравнительные амплитуды данных синусоид равны 1,0 и 0,01 (т.е. одна на 40 дБ ниже другой). На рис. 13.7, а сигнал низкой частоты (обозначенный 0 дБ) масштабируется на 1 дБ ниже полной динамической области 10-битового квантующего устройства, которую для удобства будем считать единичной. Отметим, что на рис. 13.7, а полномасштабный сигнал 0 дБ находится на 6 дБ ниже входного уровня поглощения 1 дБ. Это объясняется наличием множителя 1/2 в спектральном разложении действительного сигнала по всем ненулевым частотам. Среднее отношение сигнала к шуму квантования (SNR) для 10-битового квантующего устройства равно 60 + С дБ. Для полномасштабной синусоиды константа С равна 1,76 дБ, что делает суммарное отношение SNR примерно равным 62 дБ. При дискретном преобразовании Фурье (discrete Fourier transform — DFT, ДПФ), которое выполнялось для получения графика на рис. 13.7, длина равнялась 256. Поскольку отношение SNR преобразования увеличивается пропорционально длине преобразования (или времени интегрирования), то благодаря преобразованию SNR улучшается на 24 дБ [2] с потерей 3,0 дБ вследствие усечения. Таким образом, на выходе преобразования вершина SNR вследствие квантования равна 62 + 24 - 3 = 83 дБ. Шумовой сигнал на каждой частоте ДПФ может быть представлен как квадратный корень из суммы квадратов гауссовых случайных величин, которая описывается как случайная величина, имеющая распределение хи-квадрат с двумя степенями свободы. Дисперсия (мощность шума) равна квадрату среднего. Таким образом, имеем значительные колебания вокруг математического ожидания уровня мощности шума. Для получения устойчивой оценки нижнего уровня шума нам потребуется среднее по ансамблю. Видно, что нижний уровень шума (получен с помощью 400 средних) равен -83 дБ. К сигналу перед квантованием был добавлен псевдослучайный шум (описанный в разделе 13.2.4), чтобы рандомизировать ошибки квантования. На рис. 13.7, б и в входные сигналы ослабляются относительно полномасштабного входа на 20 и 40 дБ. Это ослабление увеличивает константу С в формуле (13.24) на 20 и 40 дБ, что проявляется как уменьшение спектральных уровней входных синусоид на эти же величины. Отметим, что входной сигнал наивысшей частоты (рис. 13.7, в), который теперь уменьшился на 80 дБ относительно полной шкалы, располагается на 3 дБ ниже среднего уровня шума преобразователя. Синусоида самой низкой частоты на рис. 13.7, в теперь ослаблена на 40 дБ относительно полной шкалы, поэтому характеризуется SNR на 40 дБ меньшим, чем для сигнала на рис. 13.7, а.

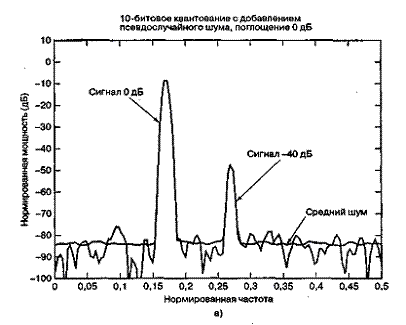
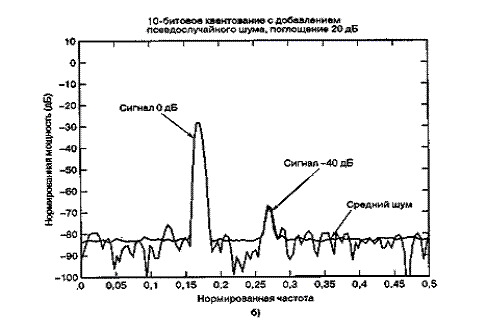
Рис. 13.7. Энергетический спектр сигналов, квантованных равномерным АЦП

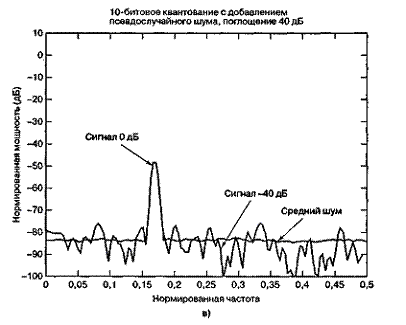
Рис. 13.7. Энергетический спектр сигналов, квантованных равномерным АЦП (прожолжение)

При минимизации среднего отношения шума к сигналу квантования мы сталкиваемся с противоречием в требованиях. С одной стороны, желательно удерживать сигналы большими по отношению к интервалу квантования q с целью получения большого SNR. С другой стороны, необходимо удерживать сигнал малым, чтобы избежать насыщения квантующего устройства. Противоречивые требования разрешаются путем масштабирования входного сигнала; в результате его среднеквадратическое значение представляет собой заданную долю полномасштабной области значений квантующего устройства. Указанная доля выбирается так, чтобы согласовать ошибки насыщения (взвешенные вероятностями их появления) с ошибками квантования (взвешиваются аналогично) и таким образом достигнуть минимального отношения шума к сигналу. Положение этой желательной рабочей точки преобразователя обсуждается в следующем разделе.

13.2.3. Насыщение

На рис. 13.8 представлено среднее NSR равномерного квантующего устройства как функция отношения уровня насыщения квантующего устройства к среднеквадратическому значению сигнала. На рисунке изображены отношения NSR сигналов с тремя различными функциями плотности вероятности: арксинус (синусообразная плотность сигнала), равномерная и гауссова.

По оси абсцисс (рис. 13.8) отложено отношение уровня насыщения квантующего устройства к среднеквадратическому уровню входного сигнала. При каждой из трех плотностей для фиксированного числа бит существует значение абсциссы, соответствующее минимуму NSR. Другими словами, для данной входной плотности можно определить уровень входного сигнала (связанный с насыщением), при котором достигается минимум NSR.

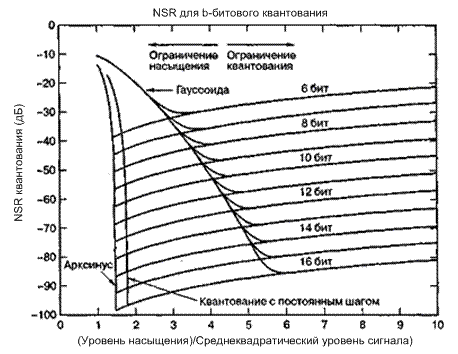
Рис. 13.8. Отношение NSR аналого-цифрового преобразователя в сравнении с отношением уровня насыщения АЦП к среднеквадратическому уровню сигнала

Уменьшенные уровни входных сигналов соответствуют большим значениям NSR на оси абсцисс и представляют собой движение вправо. Увеличенные уровни входных сигналов также соответствуют большим значениям NSR на оси абсцисс и представляют собой движение влево. Это увеличение происходит вследствие работы в области насыщения устройства квантования. Отметим, что скорость изменения отношения NSR при движении влево от оптимальной рабочей точки выше, чем при движении вправо. Например, это, в частности, верно для равномерной плотности и плотности типа арксинуса. Это свидетельствует о том, что шум насыщения более нежелателен, чем линейный шум квантования. Как следствие, если допустить ошибку в определении рабочей точки, называемой точкой атаки квантующего устройства, то будет лучше иметь ошибку на стороне превышения поглощения, чем на стороне недостаточного поглощения входного сигнала. Начало насыщения происходит в точках с различными значениями абсциссы. Для синусообразного сигнала (плотность типа

арксинуса) это происходит примерно в точке . Для треугольных сигналов (равномерная плотность) это случается примерно в точке . Для шумоподобных сигналов (гауссова плотность), когда уровень сигнала сокращается относительно насыщения, насыщение происходит непрерывно, с убывающей вероятностью. Рассмотрим в качестве примера 10-битовый АЦП, имеющий отношение NSR -60 дБ для равномерной плотности при работе на вершине насыщения и NSR -62 дБ для плотности типа арксинуса при работе на вершине насыщения. С другой стороны, тот же 10-битовый преобразователь имеет минимум NSR приблизительно в точке -52 дБ для всех плотностей, когда среднеквадратический уровень равен 1/4 уровня насыщения (точка 4 на оси абсцисс). Данный рисунок иллюстрирует, что шум насыщения более опасен, чем шум квантования. Этому можно дать достаточно простое объяснение, изучив мгновенную характеристику ошибки (как показано на рис. 13.4) и отметив, что ошибки насыщения очень велики в сравнении с ошибками квантования. Таким образом, малое насыщение, даже если оно случается нечасто, будет вносить большой вклад в средний уровень шума квантующего устройства.

Шум насыщения и шум квантования отличаются несколько по-иному. Шум квантования приближается к белому шуму. По этой причине к аналоговому сигналу до квантования могут намеренно добавляться сигналы псевдослучайного шума. Отметим, что шум насыщения подобен белому шуму только тогда, когда входной сигнал имеет широкую полосу частот и может быть гармонически связанным с входным сигналом, если тот имеет узкую полосу частот. Таким образом, влияние шума квантования может быть отфильтровано или усреднено, так как по характеристикам — это белый шум. С другой стороны, шум насыщения неотличим от содержимого полезного сигнала и в общем случае не может быть устранен с помощью последовательного усреднения или фильтрующих технологий.

На рис. 13.9 представлены дискретные преобразования Фурье того же сигнального множества, что и на рис. 13.8, квантованного 10-битовым АЦП. Кроме того, на рис. 13.9 пиковая амплитуда сигнала выбрана так, чтобы на 10% (0,83 дБ) превышать уровень насыщения АЦП. Отметим, что некоторые спектральные составляющие больше, чем сигнал в -40 дБ. Эти составляющие (шум насыщения) будут возрастать еще больше, когда отклонения сигнала будут идти глубже в режим насыщения. Чтобы увидеть существенную разницу во влиянии слишком слабого поглощения сигнала (следовательно, имеем насыщение) на выход шума АЦП, сравните этот рисунок с рис. 13.7.

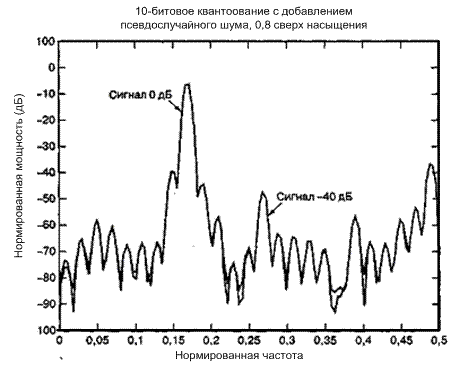
Рис. 13.9. Энергетический спектр равномерно квантованных сигналов с насыщением квантующего устройства на пиках сигнала в 0,8 дБ вне полномасштабного входного уровня

13.2.4. Добавление псевдослучайного шума

Добавление псевдослучайного шума представляет собой одно из самых разумных применений шума как полезного инженерного инструмента. Псевдослучайный шумовой сигнал — это небольшое возмущение или помеха, добавленные к измеряемому процессу, чтобы ограничить влияние малых локальных нелинейностей. Наиболее знакомой формой псевдослучайного шума является встряхивание компаса перед собственно его использованием. В данном случае имеем последовательность малых импульсов, применяемую для вывода движения стрелки из локальной области, которая имеет нелинейный коэффициент трения при малых скоростях. Более сложным примером того же эффекта является механическое псевдослучайное возмущение, применяемое к вращающимся лазерным лучам лазерного лучевого гироскопа с целью вывода гироскопа из ловушки низкоуровневой частоты, известной как мертвая полоса [3].

В случае аналого-цифрового преобразователя цель псевдослучайного шума — ограничить (или избежать) локальные разрывы (т.е. подъемы и ступени) мгновенной передаточной функции входа/выхода. Чтобы лучше представить себе влияние этих разрывов, можно перечислить ожидаемые свойства ошибочной последовательности, образованной процессом квантования, с последующим изучением действительных свойств той же последовательности. Ошибочная последовательность квантующего устройства моделируется как аддитивный шум. Давайте рассмотрим ожидаемые свойства такой последовательности шума.

1. Нулевое среднее Е{е(n)}=0

2. Белый шум Е{е(n) е(n+m)}=

3. Отсутствие корреляции с данными х(n) Е{е(n) x(n+m)}= 0

В данном случае m и n— выборочные индексы, — дельта-функция Дирака. Изучение рис. 13.10, на котором представлена последовательность выборок, образованная усекающим АЦП, позволяет сделать следующие наблюдения.

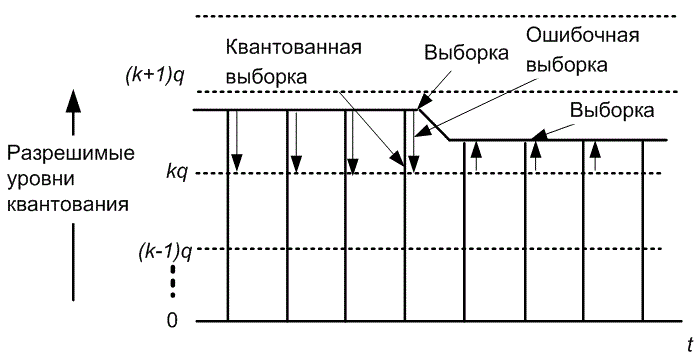
Рис. 13.10. Последовательность дискретных данных квантуется в ближайшие наименьшие уровни квантили посредством присвоенной ошибочной последовательности

1. Вся ошибочная последовательность имеет одну и ту же полярность; следовательно, ее среднее не равно нулю.

2. Последовательность не является независимой при переходе от выборки к выборке; следовательно, она не является белым шумом.

3. Последовательность ошибки коррелирует с входом; следовательно, она не является независимой.

Повторяющиеся измерения того же сигнала будут давать в результате тот же шум, и, таким образом, усреднение ни по какому числу измерений не уменьшит отклонение от истинного входного сигнала. Парадоксально, но мы хотели бы видеть этот шум "более шумным". Если шум является независимым на последовательных измерениях, усреднение будет сокращать отклонение от истинных значений. Таким образом, столкнувшись с проблемой, что получаемый шум не является тем шумом, который нам необходим, выбираем возможность изменить этот шум, добавляя к нему наш собственный. Измерения дополняются возмущением, чтобы превзойти нежелательный низкоуровневый шум устройства квантования. Дополненное возмущение в известном смысле преобразует плохой шум в хороший [4].

Пример 13.5. Линеаризация с помощью псевдослучайного шума

Предположим, рассматриваются квантующие устройства, которые могут измерять только целые величины и превращать входные данные в наименьшие ближайшие целые — процесс, называемый усечением. Сделано 10 измерений сигнала, скажем, амплитуды 3,7. При отсутствии добавочного сигнала все замеры равны 3,0. Теперь перед измерениями добавим к входной последовательности равномерно распределенную (на интервале от 0 до 1) случайную числовую последовательность. Последовательность данных имеет следующий вид.

Измерение

Необработанный

сигнал

Квантованный необработанный сигнал

Псевдослучайный шум

Суммарный сигнал

Квантованный

суммарный

сигнал

1

3,7

3,0

0,3485

4,0485

4,0

2

3,7

3,0

0,8685

4,5685

4,0

3

3,7

3,0

0,2789

3,9789

4,0

4

3,7

3,0

0,3615

4,0615

4,0

5

3,7

3,0

0,1074

3,8074

3,0

6

3,7

3,0

0,2629

3,9629

3,0

7

3,7

3,0

0,9252

4,6252

4,0

8

3,7

3,0

0,5599

4,2599

4,0

9

3,7

3,0

0,3408

4,0408

4,0

10

3,7

3,0

0,5228

4,2228

4,0

Средние =

3,0

0,4576

4,1576

3,7

Среднее псевдослучайнго

шума

0,4576

Среднее суммарного сигнала -среднее псевдослучайного шума

3,7

В этом примере для удаления смещения квантующего устройства был использован смещенный псевдослучайный шум. Среднее суммированных и преобразованных измерений (при наличии корректного измерения) в общем случае будет ближе к истинному сигналу, чем несуммированные с псевдослучайным шумом и преобразованные измерения [5, 6].

Чтобы проиллюстрировать влияние процесса добавления псевдослучайного шума на процесс квантования изменяющегося во времени сигнала, рассмотрим следующий эксперимент. Пусть синусоидальный сигнал, имеющий амплитуду 1,0, подавляется на 60 дБ. Тогда ослабляемый сигнал имеет полную амплитуду 0,001, что составляет примерно половину интервала квантования, равного 0,001957, для десятибитового равномерного устройства квантования (получается делением удвоенной амплитуды сигнала 2 на 210 - 2). Когда на округляющее квантующее устройство подается ослабленная синусоида, на выходе будут получаться в основном все нули, за исключением отдельных единиц в ±1 квантиль, что происходит в том случае, когда вход пересекает уровень ±q/2, равный 0,000979 (соответствующий наименее значимому биту АЦП). Если входной сигнал ослаблен еще на 0,23 дБ, пороговые уровни самого младшего бита никогда не будут пересекаться и выходная последовательность будет представлять собой все нули. Теперь добавим псевдослучайный шум со среднеквадратической амплитудой, равной 0,001, к ослабленной синусоиде амплитуды 0,001 так, чтобы сумма сигнала с псевдослучайным шумом регулярно пересекала уровни ±q/2 АЦП. На рис. 13.11 изображен спектр мощности, полученный путем преобразования и усреднения 400 реализаций этого суммарного сигнала. В результате ослабленный на 60 дБ сигнал на пределе разрешающей способности АЦП все еще присутствовал и, будучи точно измеренным, составил -63 дБ (-3 дБ вследствие округления). Псевдослучайный шум давал эффект расширения динамической области АЦП (как правило, с 9 до 12 дБ или с 1,5 до 2,0 бит) и повысил эффективность ступенчатой аппроксимации АЦП.

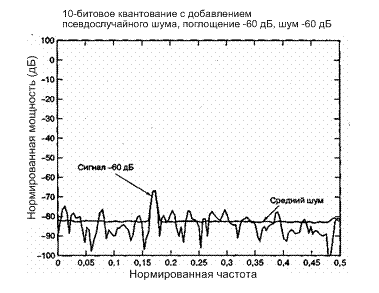
Рис. 13.11. Спектр мощности равномерного АЦП с добавлением псевдослучайного низкоуровневого сигнала

13.2.5. Неравномерное квантование

Равномерные квантующие устройства представляют собой наиболее распространенный тип аналого-цифровых преобразователей, так как они наиболее устойчивы. Под "устойчивостью" подразумевается, что они относительно нечувствительны к незначительным изменениям входных статистик. Эта устойчивость достигается в результате того, что преобразователи не настраиваются окончательно на одно конкретное множество входных параметров. Это позволяет им работать хорошо даже при наличии неопределенных входных параметров; даже незначительные изменения входных статистик приводят к несущественным изменениям выходных статистик.

Когда существует малая неопределенность в статистиках входного сигнала, можно создать неравномерное устройство квантования, которое дает меньшее отношение NSR, чем равномерное устройство квантования, использующее то же количество бит. Это реализует-

ся с помощью деления входной динамической области на неравномерные интервалы так, что мощность шума, взвешенная вероятностью появления на каждом интервале, является одинаковой. Для оптимального квантующего устройства могут быть найдены итерационные решения для границ принятия решения и размеров шагов для конкретных плотностей и малого количества бит. Эта задача упрощается путем моделирования неравномерного устройства квантования как последовательности операторов, как изображено на рис. 13.12. Сначала входной сигнал отображается с помощью нелинейной функции, называемой компрессором (compressor), в альтернативную область уровней. Эти уровни равномерно квантуются, и квантованные уровни сигнала затем отображаются с помощью дополняющей нелинейной функции, называемой экспандером (expander), в выходную область уровней. Объединяя части наименований каждой из операций COMpress и exPAND, получим название процесса: компандирование (companding).

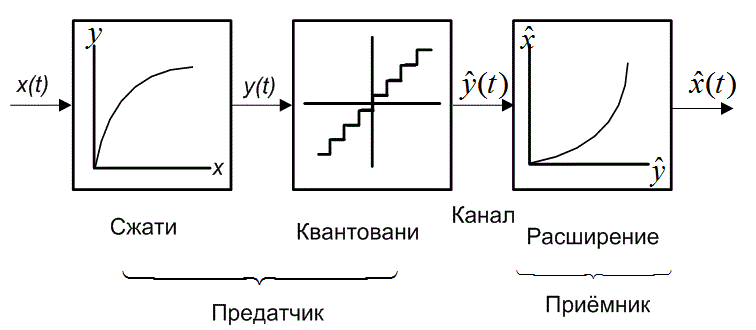
Рис. 13.12. Неравномерное устройство квантования как последовательность операторов: сжатие, равномерное квантование и расширение

13.2.5.1. Субоптимальное неравномерное квантование

Изучая характеристику компрессора у = С(х) на рис. 13.13, видим, что размеры шага квантования для выходной переменной у связаны с размерами шага квантования входной переменной х через наклон (х) (например, . Для произвольной функции плотности вероятности и произвольной характеристики компрессора можно достичь выходной дисперсии шума квантования [7].

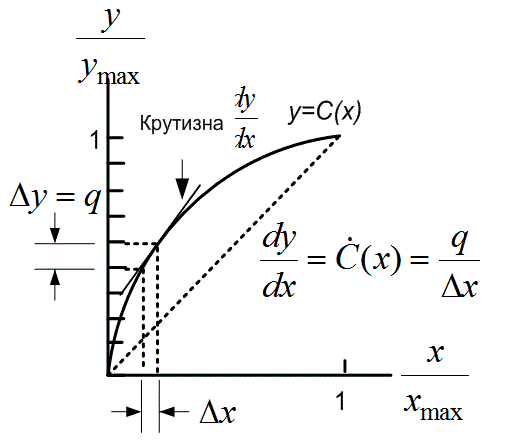
Рис. 13.13. Характеристика компрессора С(х) и оценка локального наклона

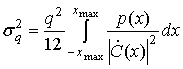(13.25)

Для определенной функции плотности вероятности может быть найдена характеристика компрессора С(х), которая минимизирует . Оптимальный закон сжатия для данной функции плотности вероятности выражается следующим образом [8].

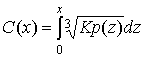(13.26)

Находим, что оптимальная характеристика сжатия пропорциональна интегралу от кубического корня от входной функции плотности вероятности. Это называется точной настройкой (fine tuning). Если компрессор настроен на работу с одной функцией плотности, а используется с другой (например, отличающейся только масштабом), говорят, что устройство квантования рассогласовано, и вследствие этого может существенно снижаться эффективность функционирования [6].

13.2.5.2. Логарифмическое сжатие

В предыдущем разделе был представлен закон сжатия для случая, когда входная функция плотности вероятности сигнала хорошо определена. Сейчас обратимся к случаю, в котором об этой функции известно мало. Это, например, происходит, когда средняя энтропия входного сигнала является случайной величиной. Например, уровень голоса случайно выбранного телефонного пользователя может варьироваться от одного экстремального значения (доверительный шепот) до другого (крик).

При неизвестной функции плотности вероятности характеристика компрессора неравномерного устройства квантования должна быть выбрана так, чтобы результирующий шум не зависел от конкретной плотности. Хотя это и представляется идеальным, достижение такой независимости может оказаться невозможным. Однако мы хотим компромисса и будем пытаться установить возможную независимость среди большого числа входных дисперсий и плотностей. Пример квантующего устройства, которое показывает отношение SNR, независимое от функции плотности вероятности входного сигнала, можно представить с помощью рис. 2.18. На этом рисунке можно наблюдать значительное отличие в отношениях NSR для входных сигналов с различными амплитудами, квантованных с помощью равномерного квантующего устройства. Для сравнения можно видеть, что неравномерное устройство квантования допускает только большие ошибки для больших сигналов. Преимущество такого подхода понятно интуитивно. Если SNR должно быть независимо от распределения амплитуды, шум квантования должен быть пропорционален входному уровню. В формуле (13.25) представлена дисперсия шума квантующего устройства для произвольной функции плотности вероятности и произвольной характеристики компрессора. Дисперсия сигнала для любой функции плотности вероятности равна следующему.

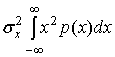(13.27)

При отсутствии насыщения SNR квантующего устройства имеет следующий вид.

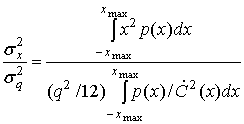(13.28)

Чтобы SNR не зависело от конкретной плотности, необходимо, чтобы числитель был масштабированной версией знаменателя. Это требование равносильно следующему.

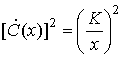(13.29)

или

(13.30)

Отсюда с помощью интегрирования находим следующее.

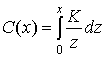(13.31)

или

C(x)=ln x+const (13.32)

Этот результат является интуитивно привлекательным. Логарифмический компрессор допускает постоянное SNR на выходе, поскольку с использованием логарифмической шкалы одинаковые расстояния (или ошибки) являются в действительности одинаковыми отношениями, а это и требуется для того, чтобы SNR оставалось фиксированным в области входного сигнала. Константа в равенстве (13.32) нужна для согласования граничных условий по дг|тхи ;упих. Учитывая эти граничные условия, получим логарифмический преобразователь следующего вида.

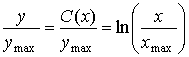(13.33)

Вид сжатия, предложенный логарифмической функцией, изображен на рис. 13.14, а. Сложность, связанная с этой функцией, состоит в том, что она не отображает отрицательные входные сигналы. Отрицательные сигналы учитываются путем добавления отраженной версии логарифма на отрицательную полуось. Эта модификация изображается на рис. 13.14 и влечет за собой следующее.

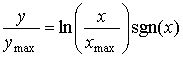(13.34)

где

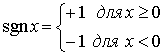
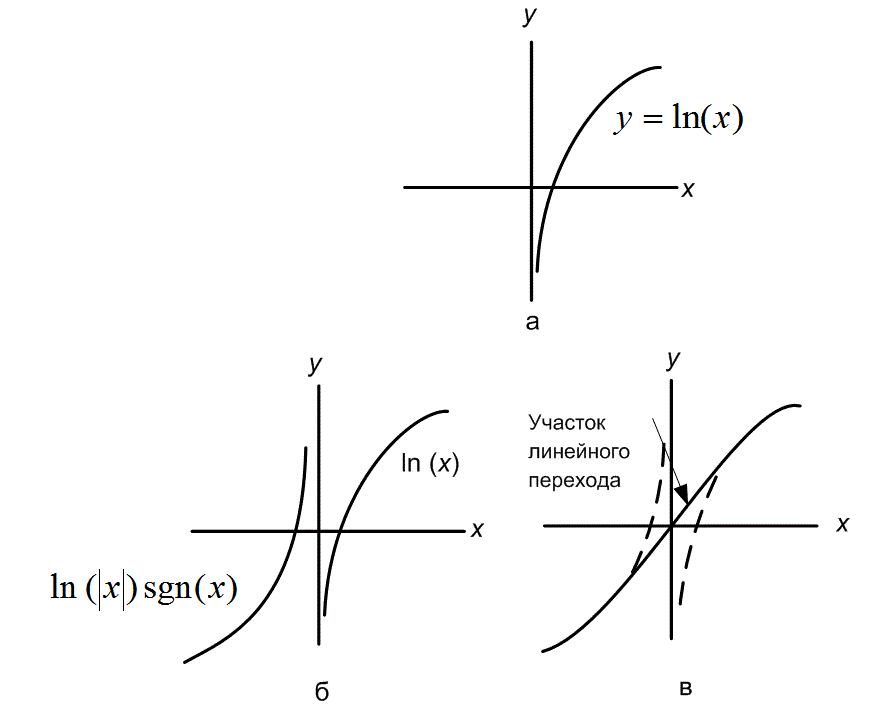
Рис. 13.14. Логарифмическое сжатие: а) прототип логарифмической функции для закона сжатия; 6) прототип функции ln|x| sgn x для закона сжатия; в) функция ln|x| sgn x с плавным соединением между сегментами.

Еще одна возникающая в этой ситуации сложность состоит в том, что сжатие, описанное равенством (13.34), не является непрерывным в начале координат; в действительности оно не имеет смысла в начале координат. Необходимо выполнить плавное соединение между логарифмической функцией и линейным отрезком, проходящим через начало координат. Существует две стандартные функции сжатия, выполняющие это соединение, —-закон компандера и А-закон компандера.

Компандер, использующий -закон. Компандер, использующий -закон, введенный компанией Bell System для использования в Северной Америке, имеет следующий вид.

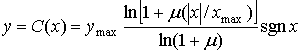(13.35)

Приблизительное поведение этого компрессора в областях, соответствующих малым и большим значениям аргумента, является следующим.

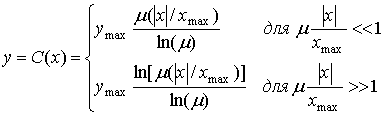(13.36)

Параметр в компандере, использующем -закон, обычно устанавливался равным 100 для 7-битового преобразователя. Позже он изменился до 255 для 8-битового преобразователя. В настоящее время стандартным североамериканским конвертером является 8-битовый АЦП с = 255.

Пример 13.6. Среднее SNR для компрессора, использующего ц-закон

Среднее SNR для компрессора, использующего ц-закон, можно оценить, подставляя выражение для ц-закона в формулу (13.28). Для положительных значений входной переменной х закон сжатия имеет следующий вид.

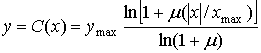(13.37)

Затем производная равна следующему.

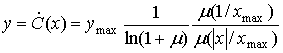(13.38)

Для значений входной переменной, для которых является большим в сравнении с единицей, производная переходит в следующее выражение.

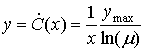(13.39)

Подставляя 1/ С(х) в формулу (13.28), получаем следующее.

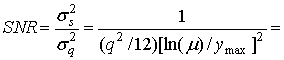(13.40)

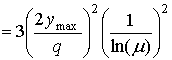(13.41)

Отношение 2ymax/q приблизительно равно числу уровней квантования (2b) для b-битового сжимающего устройства квантования. Для 8-битового преобразователя с = 255 имеем следующее.

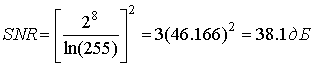(13.42)

Для сравнения на рис. 13.15 представлено отношение SNR АЦП, использующего -закон. Здесь SNR изображено для входных синусоид различной амплитуды. Там же изображен уровень 38,1 дБ, вычисленный в формуле 13.42, и SNR для линейного квантующего устройства с той же областью входных амплитуд. Как и предсказывалось, квантующее устройство, использующее -закон, поддерживает постоянное SNR для значительного диапазона входных уровней. Зубчатость кривой производительности (гранулярность квантующего устройства) вызвана логарифмической функцией сжатия. Реальные преобразователи, помимо этого, показывают дополнительную зубчатость вследствие кусочно-линейной аппроксимации непрерывной кривой -закона. На рис. 13.16 представлено дискретное преобразование Фурье пары входных синусоид относительных амплитуд 1,0 (0 дБ) и 0,01 (-40 дБ). Входной сигнал квантуется с помощью 10-битового преобразователя, использующего -закон ( = 500), и на рис. 13.16, а-в уровни сигнала ослабляются на 1,20 и 40 дБ относительно полномасштабного входа. Отметим, что уровни шума квантования для полномасштабного сигнала на рис. 13.16, а выше, чем у равномерного АЦП (-72 дБ против -83 дБ, как видно из рис. 13.7). Для ослабленных сигналов отмечаем улучшенное отношение SNR логарифмически сжимающего АЦП по сравнению с равномерным АЦП. Видно, что поскольку уровни входного сигнала уменьшились, шум квантования также снизился, и при ослаблении в 40 дБ уровень шума упал до -108 дБ. Таким образом, логарифмически сжимающие АЦП не имеют проблемы "видения" входного сигнала низкого уровня даже при ослаблении на 40 дБ, как на рис. 13.16, в, в то время как тот же сигнал теряется среди шума равномерного преобразователя, как показано на рис. 13.7, в.

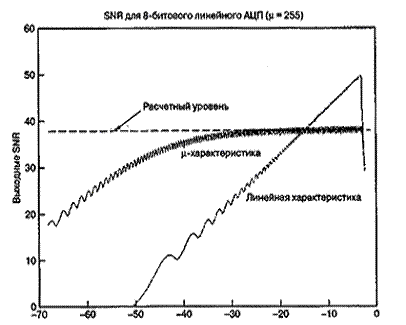
Рис. 13.15. Предсказанное и измеренное отношение SNR для АЦП, использующегоц -закон

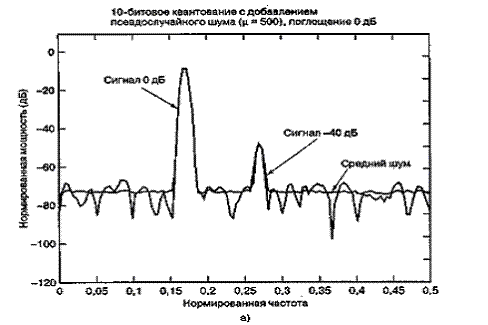
Рис. 13.16. Спектр мощности сигналов АЦП, использующего -закон

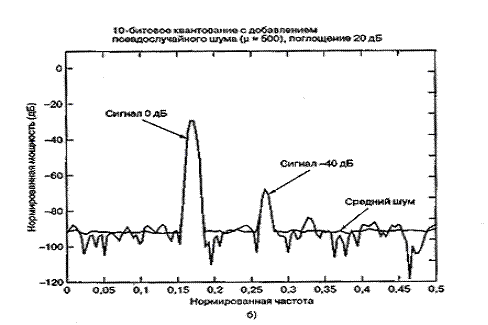
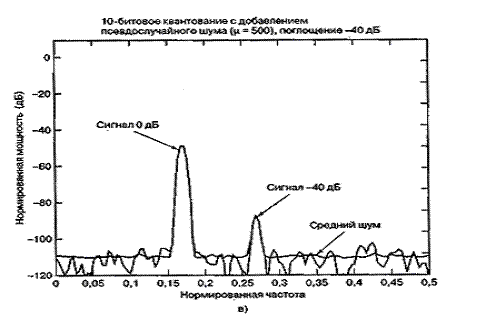
Рис. 13.16. Спектр мощности сигналов АЦП, использующего-закон (окончание)

Реальная характеристика компрессора, использующего -закон, описана формулой (13.35). Как показано на рис. 13.17, 16 сегментов линейных хорд аппроксимируют функциональное выражение на 256 возможных выходных уровнях. Восемь из этих сегментов расположены в первом квадранте, восемь — в третьем квадранте и сегмент "0" имеет один и тот же наклон в обоих квадрантах. Вдоль каждого сегмента хорды квантование является равномерным по четырем битам преобразования низшего порядка. Таким образом, 8-битовый сжимающий формат преобразования имеет следующий вид.

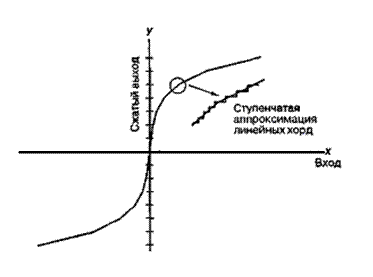
Рис. 13.17. Семибитовое сжатое квантование для 16-сегментной аппроксимации -закона

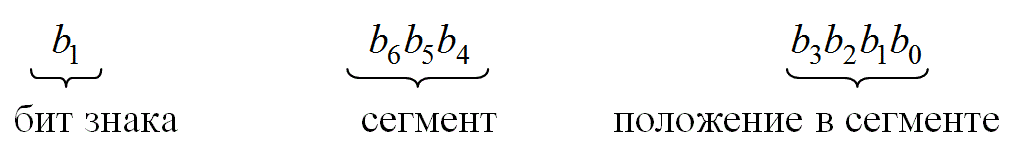
Он представляет собой кусочную аппроксимацию хордами до плавной функции и ступенчатую аппроксимацию каждой хорды, учитывающую дополнительную зубчатость в кривой SNR, которая представлена на рис. 13.15.

Компандер, использующий А-закон. Этот компандер является стандартом CCITT (Consultative Committee for International Telephone and Telegraphy — Международный консультативный комитет по телеграфии и телефонии, МККТТ), а следовательно европейским стандартом аппроксимации логарифмического сжатия. Характеристика компрессора имеет следующий вид.

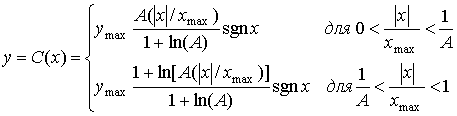(13.43)

Стандартным значением параметра А является 87,56, и (при использовании 8-битового преобразователя) SNR для этого значения равно 38,0 дБ. Сжимающая характеристика А-закона аппроксимируется подобно тому, как это делалось для компрессора, использующего -закон, — с помощью последовательности 16 линейных хорд, охватывающих выходную область. Нижние две хорды в каждом квадранте являются в действительности хордами сигнала, соответствующими линейному сегменту компрессора, использующего А-закон. Одним важным отличием между характеристиками сжатия А- и -законов является то, что стандарт А-закона имеет характеристику с нулем на границе шага квантования, в то время как стандарт -закона — характеристику с нулем в центре шага квантования. Таким образом, компрессор с A-законом не имеет нулевого значения, и следовательно, для него не существует интервала, на котором бы при нулевом входе не передавались данные.

Существует прямое отображение из формата АЦП, использующего 8-битовое сжатие с А-законом, в 12-битовый линейный двоичный код и из формата 8-битового сжатия с -законом в 13-битовый линейный код [8]. Эта операция позволяет преобразование аналоговой информации в цифровую с помощью равномерного устройства квантования с последующим отображением в меньшее число бит в кодовом преобразователе. Кроме того, это позволяет обратное отображение в приемнике (т.е. расширение) производить на числовой выборке.

Импульсно-кодовая модуляция. Одной из задач, выполняемых в ходе импульсно-кодовой модуляции (pulse-code modulation — PCM), является преобразование исходных волновых сигналов в дискретные двоичные последовательности. Эта задача производится с помощью трехэтапного процесса — дискретизации, квантования и кодирования. Процесс дискретизации изучался в главе 2, а процесс квантования — в данной главе и в главе 2. Отметим, что процесс кодирования, следующий за квантованием (см. рис. 2.2), часто воплощается на аппаратном уровне и выполняется тем же устройством, что и квантование. Вообще, процесс может быть описан следующим образом: последовательная аппроксимация аналого-цифровых преобразователей образует последовательные биты декодированных данных с помощью обратной связи, сравнения и процесса принятия решения. В процессе обратной связи постоянно задается вопрос, входной сигнал находится выше или ниже средней точки остаточного интервала неопределенности. С помощью этой технологии интервал неопределенности сокращается до половинного на каждом шаге сравнения и принятия решения до тех пор, пока интервал неопределенности не совпадет с допустимым интервалом квантования.

При последовательной аппроксимации результат каждого предыдущего решения снижает неопределенность, которая должна быть разрешена во время следующего преобразования. Аналогично результаты предшествующих преобразований аналоговой информации в цифровую могут использовать для уменьшения неопределенности, которая должна быть разрешена во время следующего преобразования. Эта редукция неопределенности достигается путем передачи каждой последующей выборке вспомогательной информации из более ранних выборок. Эта информация называется избыточной частью сигнала, и с помощью ее передачи сокращается интервал неопределенности, в котором квантующее устройство и кодер должны вести поиск следующей выборки сигнала. Передача данных — это один из методов, с помощью которых достигается снижение избыточности.